|
|
|
CAPÍTULO 3: ENERGÍA Y CANTIDAD DE MOVIMIENTO |
3.1 EL PRINCIPIO DE ENERGÍA
|
|
En el flujo permanente en canales se conservan la masa y la energía.
Por otro lado, en el flujo no permanente se conservan la masa y la cantidad de movimiento.
La energía se expresa en unidades
FL
La energía por unidad de peso se expresa en unidades de longitud [L].
Las energías potencial y cinética se pueden expresar en términos de carga, en unidades de profundidad [L].
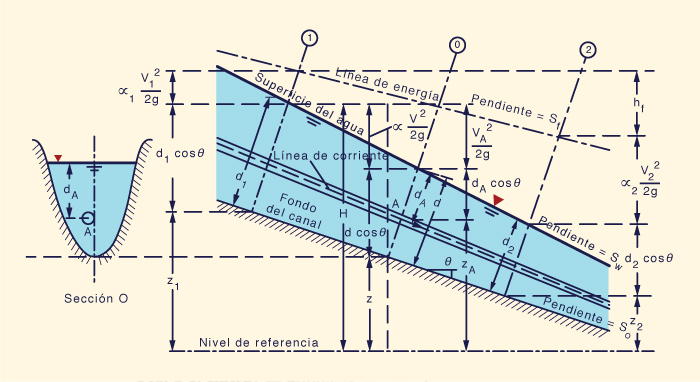
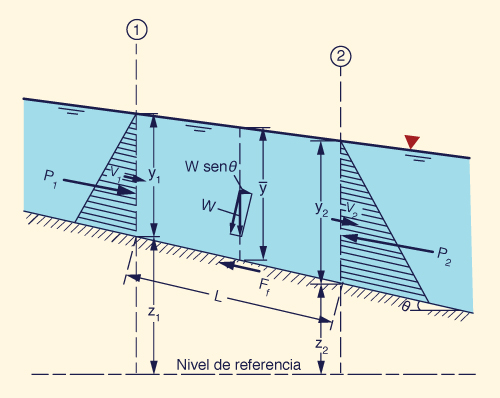
La Figura 3-1 muestra un canal con pendiente pronunciada, para el cual la carga total H correspondiente a una sección 0, con el punto A en una línea de corriente, se puede expresar de la siguiente manera:
|
VA2 H = zA + dA cos θ + ______ 2g | (3-1) |
en la cual zA = elevación del punto A por encima de un plano de referencia,
dA = profundidad del punto A por debajo de la superficie del agua, θ =
ángulo de inclinación del fondo del canal, y
|
Debido a la falta de uniformidad en una sección transversal, la carga de velocidad varía a lo largo de la profundidad y ancho.
Para una sección transversal dada, la carga de velocidad está basada en la velocidad media V.
El coeficiente de Coriolis (Sección 2.2) se utiliza para explicar la falta de uniformidad en la distribución de velocidades.
Esto conduce a la energía total para una sección dada:
|
V 2 H = z + d cos θ + α _____ 2g | (3-2) |
Para un canal de poca pendiente, cos θ ≅ 1.
Por lo tanto, la energía total se reduce a:
|
V 2 H = z + d + α _____ 2g | (3-3) |
La ley de conservación de la energía entre las secciones transversales 1 y 2 conduce a (Fig. 3-1):
|
V12 V22 z1 + d1 cos θ + α1 _____ = z2 + d2 cos θ + α2 _____ + hf 2g 2g | (3-4) |
La línea que representa la carga total es la línea de energía.
La pendiente de la línea de energía es Sf.
La pendiente de la superficie del agua es Sw y la
pendiente del fondo del canal es So, en la cual
Bajo condiciones de flujo uniforme, las tres pendientes son las mismas: Sf = Sw = So .
Para un canal de poca pendiente, la Ec. 3-4 se reduce a:
|
V12 V22 z1 + y1 + α1 _____ = z2 + y2 + α2 _____ + hf 2g 2g | (3-5) |
Para el caso de α1 = α2 ≅ 1, es decir, un canal hidráulicamente ancho, y hf = 0, la Ec. 3-4 se reduce a la ley de la conservación de la energía, o ecuación de Bernoulli:
|
V12 V22 z1 + y1 + _____ = z2 + y2 + _____ = constante 2g 2g | (3-6) |
3.2 ENERGÍA ESPECÍFICA
|
|
La Ecuación 3-6 es válida para un canal de pendiente pequeña.
En el límite, cuando el canal es horizontal, o alternativamente, cuando el canal es suficientemente corto, la Ec. 3-6 se reduce a la ley de la conservación de la energía específica.
En efecto, para z1 ≅ z2, la Ec. 3-6 se reduce a:
|
V12 V22 y1 + _____ = y2 + _____ = constante 2g 2g | (3-7) |
La Ecuación 3-7 establece la conservación de la energía específica en un canal horizontal hidráulicamente ancho.
La energía específica es:
|
V 2 E = y + _____ 2g | (3-8) |
en la cual E es la energía por unidad de peso, medida con respecto al fondo del canal, definida en términos de la profundidad de flujo y y la carga de velocidad V 2/(2g).
Dado que V = Q /A, la energía específica en términos de la descarga es:
|
Q 2 E = y + _________ 2g A 2 | (3-9) |
En el flujo permanente, Q es constante y el área de flujo A es una función de la profundidad de flujo y.
Por lo tanto, para una Q dada, la energía específica es solamente una función de y.
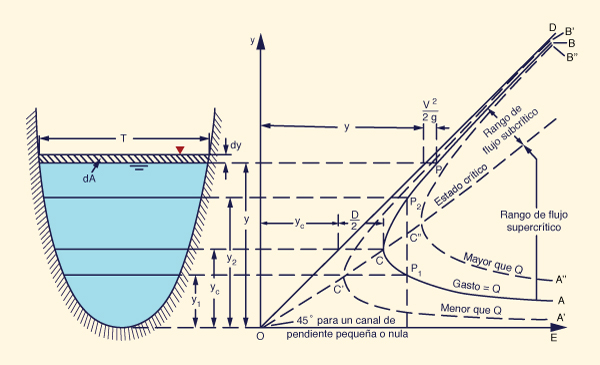
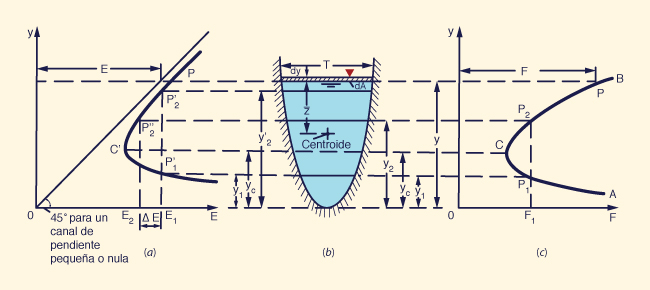
Para una sección transversal y descarga Q dadas, la gráfica de profundidad de flujo y y energía específica E resulta en la curva de energía específica mostrada en la Fig. 3-2.
Para cada valor de Q, la curva de energía específica es una función hiperbólica, con un valor mínimo de E y dos extremidades: la inferior AC y la superior BC.
|
El valor mínimo de E (en el punto C) representa el estado crítico de flujo, con profundidad crítica.
La extremidad inferior AC, con profundidades más pequeñas, describe el flujo supercrítico.
Esta extremidad es asintótica al eje horizontal.
La extremidad superior BC, con profundidades mayores, describe el flujo subcrítico.
Esta extremidad es asintótica a la línea OD de 45° de inclinación, la cual se inicia en el origen (O).
Para cualquier punto P en la curva, la abscisa representa la energía específica E y la ordenada representa la profundidad de flujo y.
Para una energía específica dada, hay dos puntos en la curva; el de abajo corresponde a un tirante pequeño y el de arriba a un tirante grande.
A éstos se les conoce como tirantes alternos.
En el punto C, los tirantes alternos se unen en un solo valor, denominado el tirante crítico, para el cual la energía específica es mínima.
Cuando el tirante es mayor que el tirante crítico el flujo es subcrítico, y cuando es menor el flujo es supercrítico.
La curva AB de la Fig. 3-2 representa la energía específica para una descarga Q dada.
La curva A'B' corresponde a una descarga menor, y la curva A"B" a una descarga mayor.
Criterio de flujo crítico
La Fig. 3-2 muestra que la profundidad crítica (flujo crítico) corresponde a la energía específica mínima.
Para comprobar esto, se diferencia la Ec. 3.9 con respecto a y y se iguala a cero:
|
dE Q 2 dA ______ = 1 - _______ ______ = 0 dy g A 3 dy | (3-10) |
El cambio diferencial en el área de flujo dA es igual al ancho de la parte superior T por el cambio diferencial en la profundidad de flujo dy (Fig. 3-2):
|
dA = T dy | (3-11) |
La Ecuación 3-10 se reduce a:
|
Q 2 Tc ________ = 1 g Ac 3 | (3-12) |
Se sabe que Dc = Ac /Tc , y Vc = Q /Ac; por lo tanto la Ec. 3-12 se reduce a:
|
Vc 2 ______ = 1 g Dc | (3-13) |
El lado izquierdo de la Ec. 3-13 es el cuadrado del número de Froude (Sección 1-3).
Por lo tanto, la condición F 2 = 1, o mejor aún, F = 1, describe la condición de caudal crítico, en la cual la energía específica es mínima.
La Ec. 3-13 se puede expresar como sigue:
|
Vc 2 Dc ______ = _____ 2g 2 | (3-14) |
la cual establece que, bajo flujo crítico, la carga de velocidad es igual a la mitad de la profundidad hidráulica.
La Figura 3-3 muestra un canal cerca del flujo crítico.
|
La Ecuación 3-14 describe la condición de flujo crítico para un canal hidráulicamente ancho (α = 1) con pendiente pequeña.
Dado un canal de gran pendiente y con sección transversal arbitraria, la condición de flujo crítico es:
|
Vc 2 Dc cos θ α ______ = __________ 2g 2 | (3-15) |
en la cual Dc es la profundidad hidráulica correspondiente al flujo crítico, medida en dirección normal al fondo.
Por lo tanto, la condición general del flujo crítico es:
|
Vc 2 _________________ = 1 (g Dc cos θ) / α | (3-16) |
El número de Froude, aplicable a cualquier canal, independientemente de la pendiente y de la sección transversal es:
|
V F = _____________________ [ (g D cos θ) / α ]1/2 | (3-17) |
3.3 FENÓMENOS LOCALES
|
|
Los cambios del flujo supercrítico a subcrítico, o de flujo subcrítico a supercrítico, ocurren frecuentemente en el flujo en canales, dependiendo de la pendiente del canal y la sección transversal.
Los cambios constituyen fenómenos locales cuando ocurren en una distancia relativamente corta.
La caída hidráulica y el salto hidráulico son ejemplos de fenómenos locales.
La caída hidráulica
La caída hidráulica se produce cuando hay una fuerte depresión en la superficie del agua, causada por un cambio brusco en la elevación.
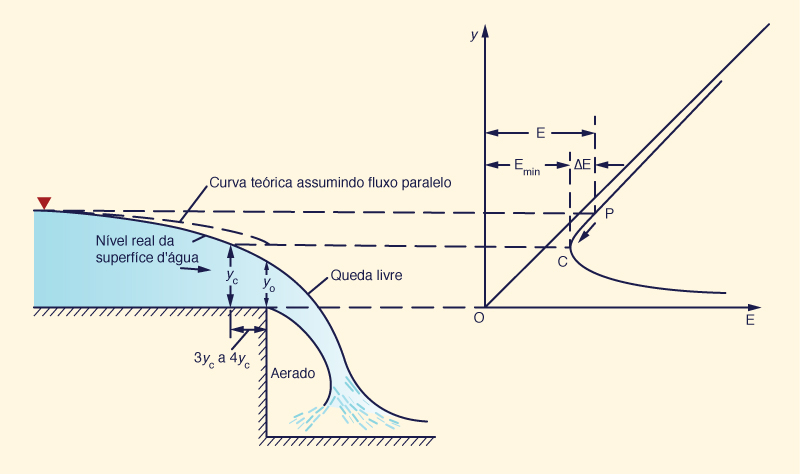
La Fig. 3-4 muestra un vertedero libre, ejemplo de caída hidráulica.
|
Por lo general, el flujo en la proximidad de un vertedero libre es rápidamente variado; por lo tanto, la profundidad medida en el borde es algo menor que la profundidad crítica calculada por la teoría del flujo paralelo.
La Figura 3-5 muestra una ilustración del flujo cerca del borde.
El nivel actual de la superficie del agua se muestra con una línea continua, mientras que la curva teórica, asumiendo flujo paralelo, se muestra con una línea discontinua.
Para los canales de poca pendiente, la profundidad crítica calculada es de aproximadamente 1.4 veces la profundidad medida en el borde; es decir,
La profundidad
|
El salto hidráulico es causado por un incremento brusco en la superficie del agua.
En un salto hidráulico el flujo cambia de supercrítico (aguas arriba) a subcrítico (aguas abajo) y es acompañado por una pérdida apreciable de energía.
La pérdida de energía depende de las condiciones del flujo aguas arriba y aguas abajo.
El salto ocurre frecuentemente en las siguientes condiciones:
-
Debajo de una compuerta reguladora (Fig. 3-6),
-
En la base (o el pie) de un vertedero, o
-
A lo largo de un canal, cuando la pendiente de fondo cambia repentinamente de alta a baja.
|
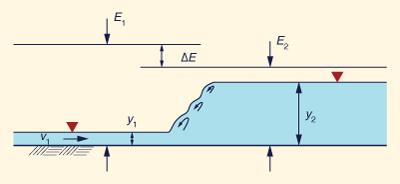
La profundidad de flujo aguas arriba del salto se llama profundidad inicial y1, y aguas abajo se llama profundidad secuente y2.
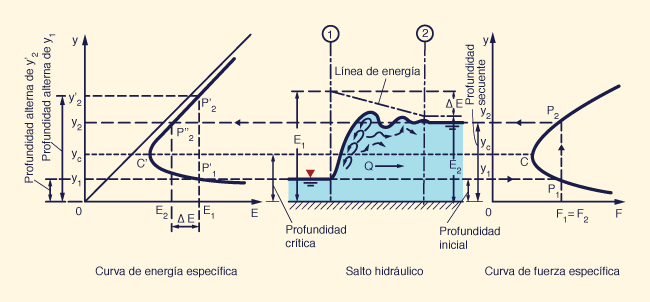
Estas profundidades se muestran en la curva de energía específica de la Fig. 3-7.
No se deben confundir con las profundidades alternas y1' y y2', las cuales son dos profundidades posibles para una energía específica.
La energía específica E1 en la profundidad inicial y1 es mayor que la energía específica E2 en la profundidad secuente y2.
La pérdida de energía debido al salto hidráulico es igual a la diferencia entre las energías específicas:
|
ΔE = E1 - E2 | (3-18) |
A la derecha de la Fig. 3-7, se muestra la curva de fuerza específica (Sección 3.5), donde las profundidades secuentes y1 y y2 tienen la misma fuerza específica: F1 = F2.
|
3.4 CANTIDAD DE MOVIMIENTO
|
|
La cantidad de movimiento M es igual a una fuerza integrada a lo largo de un período de tiempo, o la masa por la velocidad (Ec. 2-27):
|
M = ∫ F dt = m V ... [M L T -1 ] | (3-19) |
El flujo de cantidad de movimiento, o la fuerza F, de un flujo con una velocidad V a través de una sección de área A (Ec. 2-30), se repite a continuación:
|
F = β ρ V 2 A ... [F] | (3-20) |
Dado que Q = VA, el flujo de la cantidad de movimiento, o la fuerza F, ejercida por un flujo de descarga Q y velocidad V es:
|
F = β ρ Q V ... [F] | (3-21) |
De acuerdo con la segunda ley de Newton, el cambio ΔF en el flujo de cantidad de movimiento a través de un volumen de control es igual a la resultante de todas las fuerzas externas que actúan sobre dicho volumen.
Las fuerzas externas son: (1) la fuerza sobre el cuerpo, y (2) las fuerzas de superficie.
La primera fuerza es la
fuerza gravitacional expresada en la dirección del movimiento (la fuerza
Generalmente la pendiente del fondo es diferente de cero; de lo contrario, el fondo del canal sería horizontal y la componente gravitacional en la dirección del movimiento sería nula.
Las fuerzas de superficie actúan en tres lugares: (1) en la parte inferior, (2) en los lados, y (3) en la parte superior.
La fuerza inferior se debe a la fricción, la cual siempre actúa en la dirección opuesta al flujo (la fuerza Ff en la Fig. 3-8).
No existe fricción nula, pero para fines prácticos, es posible ignorar la fricción bajo ciertas condiciones.
Las fuerzas de superficie lateral son dos: una aguas arriba, la fuerza P1 en la Fig. 3-8, y otra aguas abajo, la fuerza P2.
Estas fuerzas se deben a la presión del agua, la cual puede ser
hidrostática bajo flujo paralelo, o no hidrostática bajo flujo curvilíneo convexo o cóncavo
(
La fuerza que actúa en la superficie del agua se debe a la acción del viento.
Para el flujo en canales, la fuerza del viento es despreciable, por lo cual generalmente no es considerada.
Sin embargo, la fuerza del viento no se puede ignorar en los casos de flujo superficial en lagos u océanos.
La conservación de la cantidad de movimiento en un volumen de control está dado por (Fig. 3-8):
|
ρ Q (β2V2 - β1V1) = P1 - P2 + W sin θ - Ff ... [F] | (3-22) |
En unidades de peso:
|
(γ/g) Q (β2V2 - β1V1) = P1 - P2 + W sin θ - Ff ... [F] | (3-23) |
|
La diferencia de flujo de cantidad de movimiento es igual al flujo de la sección 2 menos el flujo de la sección 1.
Las fuerzas que actúan sobre el volumen de control son positivas en la dirección del flujo y negativas en dirección opuesta.
La Ecuación 3-23 se conoce como la ecuación de balance de cantidad de movimiento o ecuación de cantidad de movimiento.
La fuerza P1 del flujo paralelo en un canal rectangular de pendiente pequeña y ancho b es:
|
P1 = (1/2) γ b y12 ... [F] | (3-24) |
De igual manera, la fuerza P2 es:
|
P2 = (1/2) γ b y22 ... [F] | (3-25) |
El peso W del volumen de control (Fig. 3-8) es:
|
W = (1/2) γ b L (y1 + y2) ... [F] | (3-26) |
El peso del volumen de control, expresado a lo largo de la dirección de movimiento (Fig. 3-8), es:
|
W sin θ = (1/2) γ b (y1 + y2) (z1 - z2) ... [F] | (3-27) |
Bajo condiciones típicas de flujo gradualmente variado, la fuerza de fricción Ff a lo largo del fondo del canal es aproximadamente igual y opuesta a la fuerza gravitacional W sin θ (Ec. 3-27).
Por lo tanto, la fuerza de fricción se puede expresar como sigue:
|
Ff = (1/2) γ b (y1 + y2) hf' ... [F] | (3-28) |
en la cual hf' = pérdida de carga debido a la fricción.
El flujo Q es:
|
Q = (1/2) (V1 + V2)
b (1/2) (y1 + y2)
... [L3 T -1]
| (3-29) |
Sustituyendo las Ecs. 3-24 a 3-29 en la Ec. 3-23 y simplificando los términos, se obtiene la siguiente ecuación:
|
V12 V22 z1 + y1 + β1 _____ = z2 + y2 + β2 _____ + hf' 2g 2g | (3-30) |
Existen varias diferencias importantes entre las Ec. 3-30 y 3-5:
-
La energía es un escalar, por lo tanto, la Ec. 3-5 es una ecuación escalar. La cantidad de movimiento es un vector, por lo que la Ec. 3-30 se deriva de una ecuación vectorial.
-
Los coeficientes de distribución de velocidades son distintos; los coeficientes de Coriolis se aplican a la Ec. 3-5 y los coeficientes de Boussinesq a la Ec. 3-30.
-
La pérdida de carga de energía hf de la Ec. 3-5 mide las pérdidas internas en el volumen de control, mientras que la pérdida de carga de fricción hf' de la Ec. 3-30 mide las pérdidas externas debidas a la acción de las fuerzas de superficie.
A pesar de que las Ecuaciones 3-5 y 3-30 son similares, no son equivalentes.
La Ecuación 3-5 se utiliza para el flujo permanente gradualmente variado, mientras que la Ec. 3-30 se utiliza para el flujo no permanente gradualmente variado .
La Ec.
El principio de la cantidad de movimiento se aplica a los problemas donde las fuerzas desempeñan un papel preponderante.
Por lo general, el principio de conservación de energía se utiliza en casos de flujo permanente gradualmente variado, mientras que el principio de conservación de la cantidad de movimiento se utiliza en el flujo no permanente gradualmente variado.
El salto hidráulico, el cual es rápidamente variado, es una excepción.
Ambos principios, energía y cantidad de movimiento, se utilizan en la solución del salto hidráulico.
3.5 FUERZA ESPECÍFICA
|
|
En los canales horizontales, la fuerza gravitacional a lo largo de la dirección del movimiento es cero.
Por lo tanto, para fines prácticos, en los canales casi horizontales, la fuerza gravitacional puede ser ignorada.
La fuerza de fricción se desarrolla a lo largo del fondo del canal; por lo tanto, cuanto más largo el canal, mayor es la fuerza de fricción.
Para un canal corto, la fuerza de fricción es pequeña y puede ser ignorada.
La fuerza de fricción nunca es nula, pero el ignorarla puede justificarse al compararla con el resto de las fuerzas presentes en el flujo de canales.
La eliminación de las fuerzas gravitacionales y de fricción en el balance del flujo de la cantidad de movimiento lleva a:
|
(γ/g) Q (β2V2 - β1V1) = P1 - P2 ... [F] | (3-31) |
Asumiendo β1 = β2 = 1, la Ec. 3-31 se reduce a:
|
(γ/g) Q (V2 - V1) = P1 - P2 ... [F] | (3-32) |
Dado que V1 = Q / A1, y V2 = Q / A2:
|
Q 2 Q 2 (γ/g) ( ______ - ______ ) = P1 - P2 ... [F] A2 A1 | (3-33) |
La fuerza de presión P que actúa en una sección de área A y distancia z̄ medida desde el centroide del área hasta la superficie del agua [Fig. 3-9 (b)] es:
|
P = γ z̄ A ... [F] | (3-34) |
|
Por lo tanto:
|
P1 = γ z̄1 A1 ... [F] | (3-35) |
|
P2 = γ z̄2 A2 ... [F] | (3-36) |
Sustituyendo las Ecs. 3-35 y 3-36 en la Ec. 3-33, y dividiendo por el peso específico (peso unitario) γ:
|
Q 2 Q 2 ______ + z̄1 A1 = ______ + z̄2 A2 ... [L 3] gA1 gA2 | (3-37) |
En general, la fuerza específica se define como sigue:
|
Q 2 F = ______ + z̄ A ... [L 3] gA | (3-38) |
La Ecuación 3-37 establece que la fuerza específica se conserva en el flujo de canales en un canal horizontal pequeño, es decir, F1 = F2.
Nótese que la fuerza específica es una fuerza por unidad de γ (el peso por unidad de volumen); por lo tanto, la fuerza específica tiene las unidades de volumen [L3].
La curva de la fuerza específica que se muestra en la Fig. 3-9 (c) se obtiene graficando F en las abscisas e y en las ordenadas.
Esta curva es similar a la curva de la energía específica [Fig. 3-9 (a)], pero con algunas diferencias.
La extremidad de AC se acerca al eje horizontal asintóticamente hacia la derecha.
La extremidad BC se eleva hacia arriba y se extiende sin límite a la derecha.
Dado un valor de la fuerza específica F1, la curva tiene dos profundidades posibles: y1 y y2.
Éstas son las profundidades inicial y secuente, respectivamente, de un salto hidráulico.
En el punto C
Esta es la misma profundidad crítica obtenida en base a consideraciones de energía específica; ver Fig. 3-9 (a).
El criterio del flujo crítico en la fuerza específica
Así como en el caso de la energía específica, para probar que la fuerza específica mínima corresponde al criterio de flujo crítico se debe diferenciar la Ec. 3-38 con respecto a y, lo cual resulta en:
|
dF Q 2 dA d(z̄A) ______ = - _______ ______ + ________ = 0 dy g A 2 dy dy | (3-39) |
Para un cambio en la profundidad dy, el cambio correspondiente d(z̄A) en el momento estático del área mojada con respecto a la superficie libre es:
|
d(z̄A) = [A (z̄ + dy) + (1/2) T (dy)2] - z̄A | (3-40) |
Conforme es usual en el cálculo diferencial, el término de segundo orden en la Ec. 3-40 es despreciable. Así:
|
d(z̄A) = A dy | (3-41) |
Por lo tanto, la Ec. 3-39 se reduce a:
|
dF Q 2 dA ______ = - _______ ______ + A = 0 dy g A 2 dy | (3-42) |
Simplificando la Ec. 3-42:
|
Q 2 dA ______ ______ = A g A 2 dy | (3-43) |
Dado que dA /dy = T, Q /A = V, y A /T = D, la Ec. 3-43 se reduce a:
|
V 2 ______ = 1 g D | (3-44) |
el cual es el cuadrado del número de Froude:
|
Vc 2 F 2 = ______ = 1 g Dc | (3-45) |
La Ecuación 3-45 es el criterio de flujo crítico, aplicable tanto a curvas de energía específica como a curvas de fuerza específica (cantidsd de movimiento específica).
Cabe mencionar que la profundidad secuente y2 es siempre menor que la profundidad alterna alta y2' (Fig. 3-7).
Además, la energía E2 es siempre menor que la energía E1, mientras que la fuerza específica F2 sigue siendo igual a la fuerza específica F1 [Fig. 3-7 y Fig. 3-9 (c)].
A fin de mantener una fuerza específica constante, la profundidad de flujo debe incrementarse de y1 a y2, con la pérdida de una cierta cantidad de energía.
La pérdida de energía es igual a: ΔE = E1 - E2.
Esta situación ocurre en el salto hidráulico, donde las fuerzas específicas antes y después del salto son iguales, pero con una consecuente pérdida de energía (Fig. 3-10).
|
Fuerza específica por unidad de ancho del canal
En un canal hidráulicamente ancho o, en su defecto, en un canal rectangular, la fuerza específica por unidad de ancho b es:
|
F q 2 y 2 ___ = _____ + _____ ... [L 2] b gy 2 | (3-46) |
en la cual q = Q /b.
La fuerza específica por unidad de ancho del canal b, se puede describir en términos de velocidad media V = q/y, como sigue:
|
F V 2y y 2 ___ = _______ + _____ ... [L 2] b g 2 | (3-47) |
Fuerza específica en unidades de fuerza
En unidades de fuerza, la fuerza específica es:
|
γQ 2 γF = _______ + γ z̄ A ... [F] gA | (3-48) |
En unidades de fuerza, la fuerza específica por unidad de ancho es:
|
γF γq 2 γy 2 ____ = ______ + ______ ... [F L -1] b gy 2 | (3-49) |
En unidades de fuerza, y en términos de velocidad media V, la fuerza específica por unidad de ancho b es:
|
γF γV 2y γy 2 ____ = _________ + _____ ... [F L -1] b g 2 | (3-50) |
|
Ejemplo 3-1: Ecuación del salto hidráulico Derivar la relación entre la profundidad inicial (y1) y secuente (y2) en un salto hidráulico (Eq. 9-13) en un canal rectangular de lecho horizontal (Fig. 3-11).
De la ecuación 3-47, el balance de la fuerza específica entre aguas arriba y aguas abajo en un salto hidráulico es:
Reemplazando F1 = V1 /(gy1)1/2:
Factorizando:
La solución de la ecuación cuadrática entre corchetes es:
la cual es la misma que la Ec. 9-13. |
PREGUNTAS
|
|
-
¿Cuál es la diferencia entre energía total y energía específica?
-
¿Cuál es el flujo crítico en términos de la energía específica?
-
¿A que se debe la caída hidráulica?
-
¿Por qué la profundidad de flujo en un vertedero de caída libre es menor que la profundidad crítica?
-
¿A que se debe el salto hidráulico?
-
¿Porqué la cantidad de movimiento es no permanente?
-
¿Cuál es la fuerza de cuerpo (de agua) considerada en el flujo en canales?
-
¿Cuál es la magnitud de la fuerza de cuerpo (de agua) en un canal horizontal?
-
¿Cuál es la diferencia entre las profundidades alternas y secuentes?
-
¿Dónde se aplica la fuerza específica?
-
¿Para qué tipo de problemas se usa la fuerza específica?
PROBLEMAS
|
|
-
Derivar la relación para el flujo q por unidad de ancho bajo una compuerta, en función de la profundidad aguas arriba y1 y la de aguas abajo y3 (Fig. 3-12).
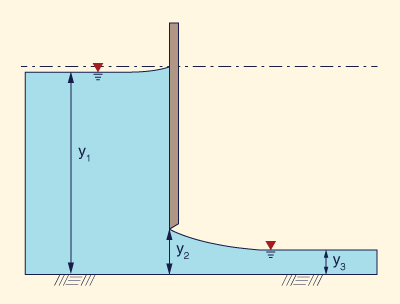
Fig. 3-12 Flujo bajo una compuerta.
[Vea también Video de laboratorio: Compuerta]. -
Demostrar que la ecuación derivada del problema anterior (Problema 1) es matemáticamente equivalente a la ecuación basada en y1 y y2 utilizada en CANAL EN LÍNEA 13.
Utilizando el principio de la energía específica, derivar la fórmula para el ancho adimensional de una contracción por el cual se fuerza el flujo crítico (Fig. 3-13) [Henderson (1966), p. 267].
bc (27)1/2 F1
σ = _____ = _______________
b1 (2 + F12) 3/2(3-55) 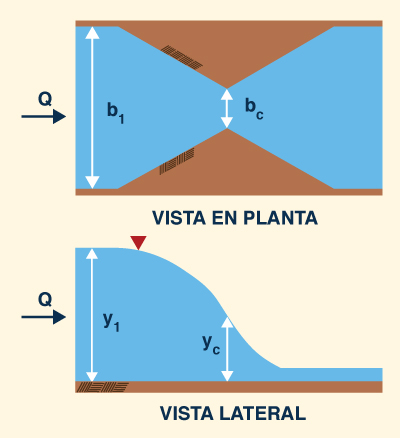
Fig. 3-13 Contracción de ancho crítico utilizando energía específica.
-
Usar CANAL EN LÍNEA 17 para calcular el ancho de garganta bc para las siguientes condiciones aguas arriba: y1 = 2.2 m, v1 = 1.2 m/s, y b1 = 3.2 m. ¿Cuál sería el ancho de la garganta si el ancho del canal aguas arriba es b1 = 2.2 m?
-
Usando el principio de la fuerza específica, demostrar que la fuerza fo (en kN/m) ejercida por una obstrucción ubicada en el lecho de un canal hidráulicamente ancho es:
1 - α 2 1
fo = - γ y12 [ ________ + ( 1 - _____ ) F12 ]
2 α(3-56) en la cual γ = peso unitario del agua, F1 = número de Froude aguas arriba, y1 = profundidad del flujo aguas arriba, y
α = y2/y1, donde y2 = profundidad del flujo aguas abajo (después de la obstrucción). Dado que q = 1.5 m2/s,v1 = 1.0 m/s, y α = 0.91, calcule la fuerza fo. Asumiendo que el flujo va de izquierda a derecha, en qué dirección está actuando la fuerza fo? -
Usando el principio de la fuerza específica, derivar la fórmula para el ancho adimensional de una contracción de canal, el cual fuerza el flujo crítico a través de él (Fig. 3-14) [modificado de Henderson (1966), p. 267].
bc (3)3/4 F3
σ = _____ = _________________
b3 (1 + 2 F32) 3/4(3-57) 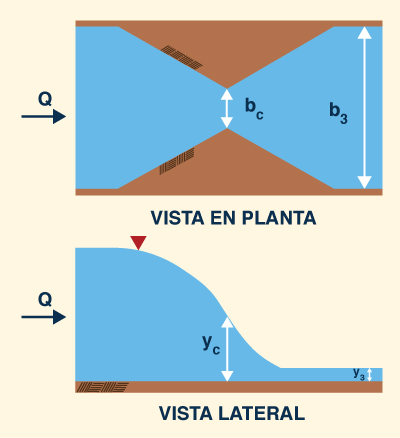
Fig. 3-14 Contracción de ancho crítico usando fuerza específica.
-
Usando ENLíNEA CONTRACCIÓN LÍMITE, calcular los coeficientes de contracción límite utilizando ambos principios de energía y cantidad de movimiento, para un número de Froude F = 0.3.
-
Usando ENLíNEA CONJUNTO CONTRACCIÓN LÍMITE, calcular los coeficientes de contracción límite utilizando ambos principios de energía y cantidad de movimiento, para números de Froude en el rango
0.1 ≤ F ≤ 2.0, a intervalos de 0.1. -
Un salto hidráulico sumergido ocurre inmediatamente aguas abajo de una compuerta en un canal rectangular. Utilizando el principio de la cantidad de movimiento, demostrar que la relación de profundidad sumergida ys entre la profundidad aguas abajo y2 es:
ys y2
_____ = [ 1 + 2 F22 ( 1 - _____ ) ] 1/2
y2 y1(3-58) 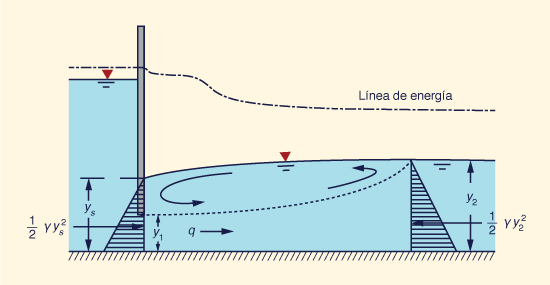
Fig. 3-15 El salto hidráulico sumergido aguas abajo de una compuerta.
BIBLIOGRAFÍA
|
|
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, Nueva York.
Henderson, F. M. 1966. Open channel flow. Macmillan, Nueva York.
| http://hidraulicadecanales.sdsu.edu |
|
150714 10:00 |