CAPÍTULO 7:
FLUJO PERMANENTE GRADUALMENTE VARIADO |
7.1 ECUACIÓN DEL FLUJO GRADUALMENTE VARIADO
El flujo es gradualmente variado cuando la descarga Q
es constante pero las demás variables hidráulicas
(A, V, D, R, P, etc.) varían
gradualmente en el espacio.
Las suposiciones básicas
de flujo gradualmente variado son:
-
El flujo es permanente, es decir, ninguna de las variables hidráulicas varían en el tiempo.
-
Las líneas de corriente son esencialmente paralelas; por lo tanto, la distribución de presiones en la
vertical es hidrostática, es decir, proporcional a la profundidad de flujo.
-
La pérdida de carga es la misma que la que corresponde
a un flujo uniforme; por lo tanto, la fórmula del flujo
uniforme puede ser usada para evaluar la pendiente de la línea de energía.
-
El valor de n de Manning es el mismo que para el flujo uniforme.
Otras suposiciones del flujo gradualmente variado son:
La pendiente del canal es pequeña.
El factor de corrección de presión cosθ ≅ 1.
El atrapamiento de aire es insignificante.
-
La conducción es una función exponencial de la
profundidad de flujo (excepto para el caso de alcantarillas circulares).
-
La rugosidad (n de Manning) es independiente de
la profundidad de flujo (esto es solamente una aproximación) y
es constante a lo largo del tramo.
|
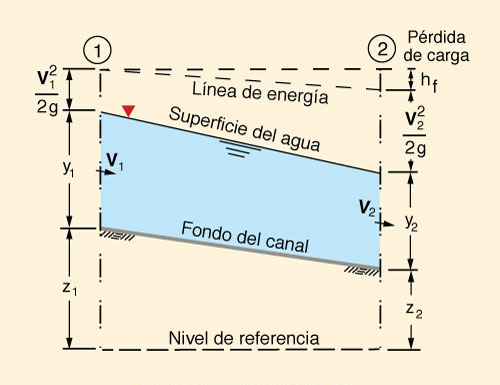
Fig. 7-1 La energía en el
flujo en canales.
|
|
En el flujo gradualmente variado, el gradiente de la carga hidráulica es (Fig. 7-1):
dH d V 2
_____ = ___ ( z + y + _____ ) = - Sf
dx dx 2g
| (7-1) |
El signo negativo para la pendiente de
fricción Sf es necesario ya que la dirección de
flujo es de izquierda a derecha, mientras que por costumbre, la
derivada se toma de derecha a izquierda.
La pendiente de fricción es:
en la cual ΔL = longitud del tramo del canal.
El gradiente de la energía específica es:
dE d V 2 dz
_____ = ___ ( y + _____ ) = - ____ - Sf
dx dx 2g dx
| (7-3) |
El gradiente del lecho del canal, o la pendiente del fondo, es:
dz z2 - z1
_____ = ________
dx ΔL
| (7-4) |
dz z1 - z2
- _____ = ________ = So
dx ΔL
| (7-5) |
Entonces,
el gradiente de la energía específica es:
dE d V 2
_____ = ___ ( y + _____ ) = So - Sf
dx dx 2g
| (7-6) |
En el flujo permanente: Q = V A = constante.
Por lo tanto:
d Q 2
____ ( y + _______ ) = So - Sf
dx 2g A2
| (7-7) |
dy d Q 2
_____ + _____ ( _______ ) = So - Sf
dx dx 2g A2
| (7-8) |
dy Q 2 dA
_____ - ( ______ ) _____ = So - Sf
dx g A3 dx
| (7-9) |
dy Q 2 dA dy
_____ - ( ______ ) _____ _____ = So - Sf
dx g A3 dy dx
| (7-10) |
Usando la Ecuación 3-11:
dy Q 2 T dy
_____ - ( ________ ) _____ = So - Sf
dx g A3 dx
| (7-11) |
Entonces, el gradiente de la profundidad es:
dy So - Sf
_____ = _______________________
dx 1 - [(Q 2 T ) / (g A3)]
| (7-12) |
La pendiente de fricción basada en la ecuación de Chezy
(Ecs. 5-10 y 2-4) es:
Q 2
Sf = ____________
C 2 A2 R
| (7-13) |
Debido a que R = A / P :
Q 2 P
Sf = _________
C 2 A3
| (7-14) |
Sustituyendo
la Ec. 7-14 en la Ec. 7-12, el gradiente de la
profundidad es:
dy So - [(Q 2 P ) / (C 2 A3)]
_____ = ___________________________
dx 1 - [(Q 2 T ) / (g A3)]
| (7-15) |
dy So - (g/C 2) (P / T ) [(Q 2 T ) / (g A3)]
_____ = _______________________________________
dx 1 - [(Q 2 T ) / (g A3)]
| (7-16) |
El cuadrado del número de Froude es (Ec. 3-12):
Q 2 T
F 2 = _________
g A3
| (7-17) |
Substituyendo
la Ec. 7-17 en la Ec. 7-16:
dy So - (g/C 2) (P / T ) F 2
_____ = _________________________
dx 1 - F 2
| (7-18) |
Sustituyendo la Ec. 5-12
en la Ec. 7-18:
dy So - f (P / T ) F 2
_____ = _____________________
dx 1 - F 2
| (7-19) |
Por lo tanto, el gradiente de la profundidad (dy/dx)
es una función de:
-
La pendiente del canal So,
-
El coeficiente de fricción f,
-
La relación perímetro mojado-ancho de superficie P / T, y
-
El número
de Froude.
Para dy/dx = 0, la Ec. 7-19 se reduce a la ecuación de flujo uniforme:
So = f (P / T ) F 2
| (7-20) |
Para F = 1,
la Ec. 7-20 se reduce al flujo uniforme crítico:
So = f (Pc / Tc ) = Sc
| (7-21) |
en la cual Sc = pendiente crítica, es decir,
la pendiente del canal para la cual el flujo es crítico.
En términos de la pendiente crítica, el gradiente de la profundidad es (Ec. 7.21):
dy So - (P / T ) (Tc / Pc )
Sc F 2
_____ = ________________________________
dx 1 - F 2
| (7-22) |
Para (P / T ) ≅ (Pc / Tc ), es decir, para una relación constante
(P / T), la Ec. 7-22 se reduce a:
dy So -
Sc F 2
_____ = _______________
dx 1 - F 2
| (7-23) |
El gradiente de la profundidad
se puede escribir como sigue:
Sustituyendo la Ec. 7-24 en la Ec. 7-23, resulta en:
Sy (So / Sc) - F 2
____ = __________________
Sc 1 - F 2
| (7-25) |
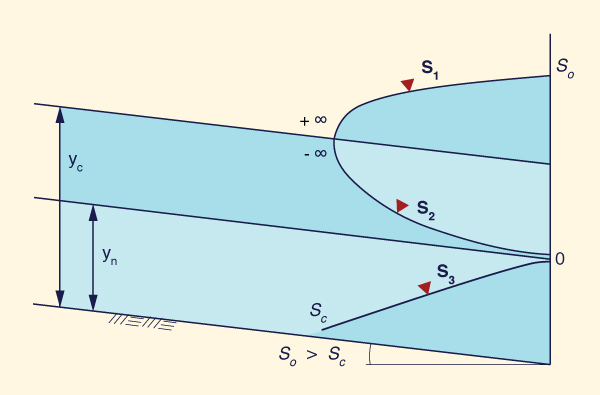
La Ecuación 7-25 (o la Ec. 7-23) es la ecuación
de flujo permanente gradualmente variado (Fig. 7-2).
El gradiente de profundidad Sy
es solamente una función de:
La pendiente del canal
So,
La pendiente crítica Sc, y
El número de Froude F.
|
Fig. 7-2 Ilustración del flujo permanente gradualmente variado.
|
|
Nota sobre el uso de la Ec. 7-25
La Ecuación 7-25 es aplicable únicamente en el caso
(P/T) (Tc/Pc) = 1,
que es el mismo que
(P/T) = (Pc/Tc ); es decir, para una
relación constante (P/T), independientemente de la profundidad de flujo.
Esta condición es menos estricta que la condición (asintótica)
del canal hidráulicamente ancho, para el cual
(P/T) = 1.
Por lo tanto, para un canal hidráulicamente ancho,
donde P ≅ T, se deduce que:
(P/T) (Tc/Pc) ≅ 1.
Por lo cual la Ec. 7-25 es aplicable a canales hidráulicamente anchos.
|
7.2 CARACTERÍSTICAS DE LOS PERFILES
En la Ecuación 7-25, el signo del lado izquierdo (SLI) es el
de Sy (numerador),
ya que Sc (denominador) es siempre positivo
(la fricción es siempre positiva).
El signo de
Sy (es decir, el
signo de la SLI) puede ser una de tres posibilidades:
-
Un valor positivo, que lleva a un FLUJO RETARDADO (REMANSO),
-
Un valor cero, que lleva a un FLUJO UNIFORME (NORMAL), o
-
Un valor negativo, que lleva a un FLUJO ACELERADO (ABATIMIENTO).
En el lado derecho de la Ec. 7-25, hay tres posibilidades para el numerador
(USDA Soil Conservation Service, 1971):
- So / Sc > F 2,
lo cual lleva al FLUJO SUBNORMAL,
- So / Sc = F 2,
lo cual lleva al FLUJO NORMAL, o
- So / Sc < F 2,
lo cual lleva al FLUJO SUPERNORMAL.
Hay tres posibilidades para el denominador:
- 1 > F 2, lo cual lleva al FLUJO SUBCRÍTICO,
- 1 = F 2, lo cual lleva al FLUJO CRÍTICO, o
- 1 < F 2, lo cual lleva al FLUJO SUPERCRÍTICO.
Dadas las desigualdades anteriores, surgen tres tipos (o familias)
de perfiles de superficie del agua, las cuales se muestran en
la Tabla 7-1.
El número total de perfiles es 12. La Tabla 7-2 muestra un resumen de los perfiles.
Tabla 7-1 Tipos de perfiles de superficie del agua.
| Tipo | Descripción
| Numerador y denominador del lado derecho
de la Ec. 7-25
|
SLI | Perfil
del flujo
|
I
| Flujo subnormal/subcrítico |
Ambos numerador y denominador son positivos
|
+ |
Retardado | |
II | A
| Flujo subnormal/supercrítico | Numerador positivo y denominador negativo |
- |
Acelerado | | B | Flujo supernormal/subcrítico | Numerador negativo y denominador positivo |
- |
Acelerado | |
III | Flujo supernormal/supercrítico
| Ambos numerador y denominador son negativos |
+ |
Retardado |
Tabla 7-2 Resumen de los perfiles de superficie del agua.
| Familia
| Estado
| Regla
| So > Sc
| So = Sc
| So < Sc
| So = 0
| So < 0
| I
| Retardado
(Remanso)
| 1 > F 2 < (So / Sc)
| S1
| C1
| M1
| -
| -
|
| II | A
| Acelerado
(Abatimiento)
| 1 < F 2 < (So / Sc)
| S2
| -
| -
| -
| -
|
| B
| Acelerado
(Abatimiento)
| 1 > F 2 > (So / Sc)
| -
| -
| M2
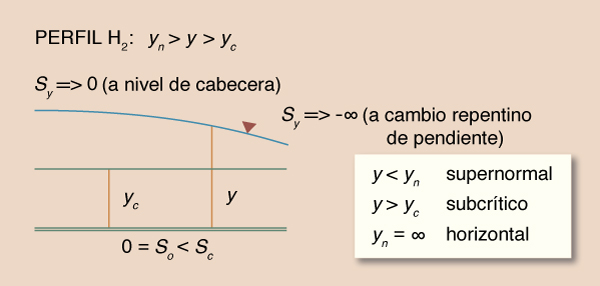
| H2
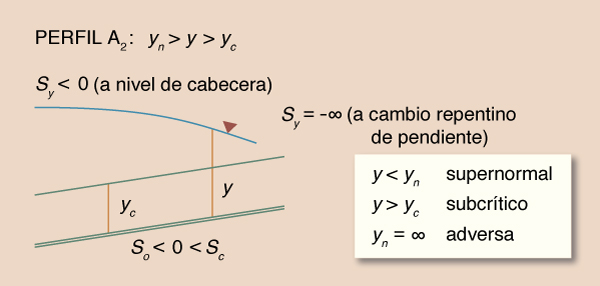
| A2
|
| III
| Retardado
(Remanso)
| 1 < F 2 > (So / Sc)
| S3
| C3
| M3
| H3
| A3
|
| |
|
Tipo I
En la familia Tipo I, el flujo es subnormal/subcrítico.
Por lo tanto, la regla es:
1 > F 2 <
(So / Sc )
| (7-26) |
la cual es lo mismo que:
La ecuación 7-27 establece que So puede ser menor que, igual a, o mayor que Sc .
Esto da lugar a tres tipos de perfiles:
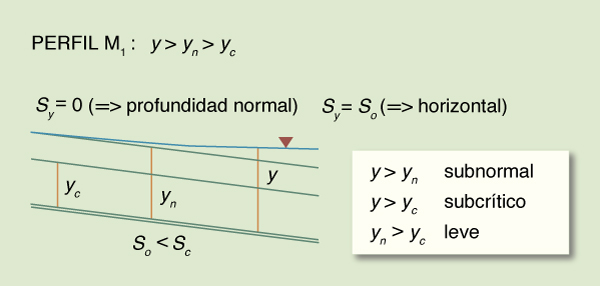
M1: So < Sc
|
Fig. 7-3 Perfil M1 de la superficie del agua .
|
|
El gradiente de profundidad Sy
varía de asintótico a So
(es decir, asintótico a la horizontal) en el extremo aguas abajo, a asintótico a cero (es decir, asintótico a la profundidad normal) en el extremo aguas arriba.
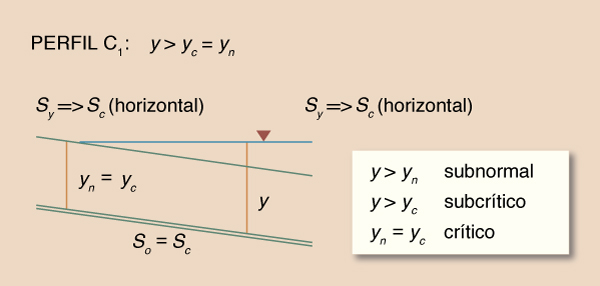
C1: So = Sc
|
Fig. 7-4 Perfil C1 de la superficie del agua.
|
|
El gradiente de profundidad Sy varía de
Sc en el extremo
aguas abajo, a Sc en el extremo aguas arriba, es decir,
el perfil de la superficie del agua es una línea horizontal.
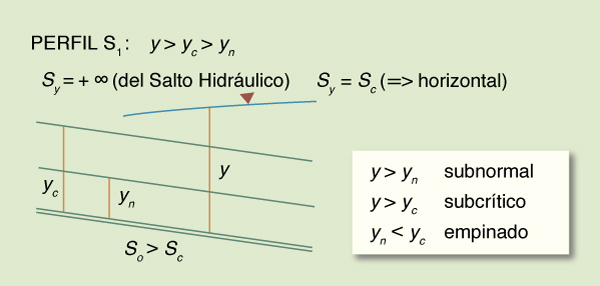
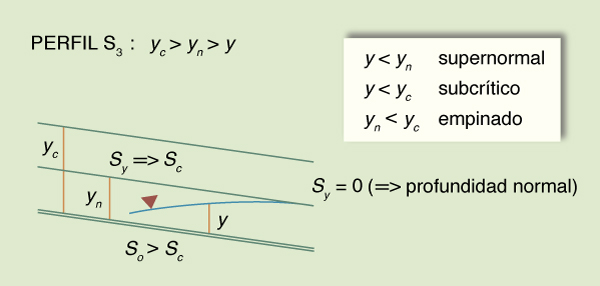
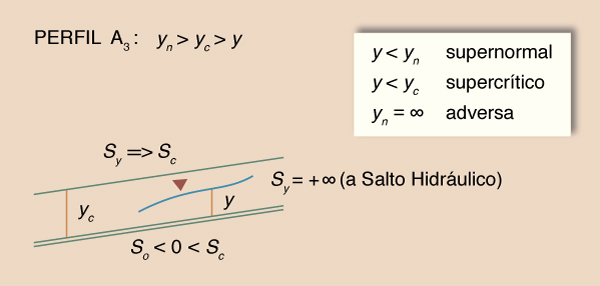
S1: So > Sc
|
Fig. 7-5 Perfil S1 de la superficie del agua.
|
|
El gradiente de profundidad
Sy varía de asintótico a
So (es decir, asintótico a la horizontal)
en el extremo aguas abajo, a asintótico a + ∞
(es decir, asintótico al salto hidráulico) en el extremo aguas arriba.
Dado que
y
por lo tanto
Así:
Quiere decir que en la familia de perfiles de superficie del agua Tipo I, no son posibles los perfiles horizontales (H) ni adversos (A).
|
|
Tipo II A
En la familia Tipo II A, el flujo es subnormal/ supercrítico.
Por lo tanto, la regla es:
1 < F 2 <
(So / Sc )
| (7-32) |
lo cual es lo mismo que:
La Ecuación 7-33 establece que So solamente puede ser mayor que
Sc, lo cual da lugar a un solo perfil:
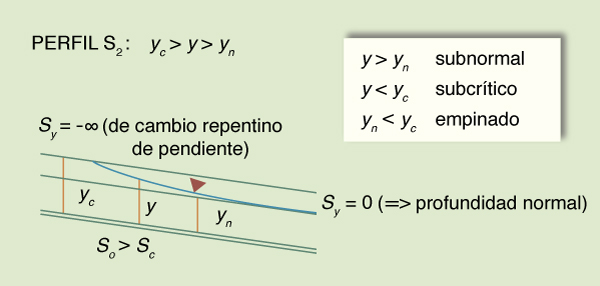
S2: So > Sc
|
Fig. 7-6 Perfil S2 de la superficie del agua .
|
|
El gradiente de profundidad Sy varía de
- ∞ (es decir, asintótico a un cambio repentino de pendiente de fondo)
en el extremo aguas arriba, a asintótico a cero
(es decir, asintótica a la profundidad normal) en el extremo aguas abajo.
Dado que:
y
Por lo tanto:
Así:
Quiere decir que en la familia de perfiles de superficie del agua Tipo II, no son posibles los perfiles horizontales (H) ni los adversos (A).
|
|
Tipo II B
En la familia Tipo II B, el flujo es supernormal / subcrítico.
Por lo tanto, la regla es:
1 > F 2 >
(So / Sc )
| (7-38) |
la cual es lo mismo que:
La ecuación 7-39 establece que So puede ser menor que
Sc, igual a 0, o menor que 0.
Esto da lugar a tres tipos de perfiles:
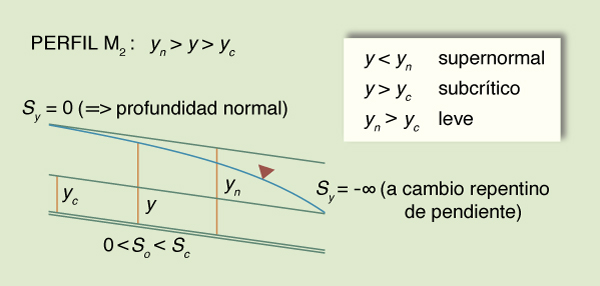
M2: 0 < So < Sc
|
Fig. 7-7 Perfil M2 de la superficie del agua.
|
|
El gradiente de profundidad Sy varía de
- ∞ (es decir, cambio repentino en la pendiente de fondo) en el extremo aguas abajo, a
asintótica a cero (es decir, asintótica a la profundidad normal)
en el extremo aguas arriba.
|
|
Tipo III
En la familia Tipo III, el flujo es supernormal / supercrítico.
Por lo tanto, la regla es:
1 < F 2 >
(So / Sc )
| (7-44) |
la cual es lo mismo que:
La ecuación 7-45 establece que So puede ser menor que, igual a, o mayor que
Sc.
Esto da lugar a cinco tipos de perfiles:
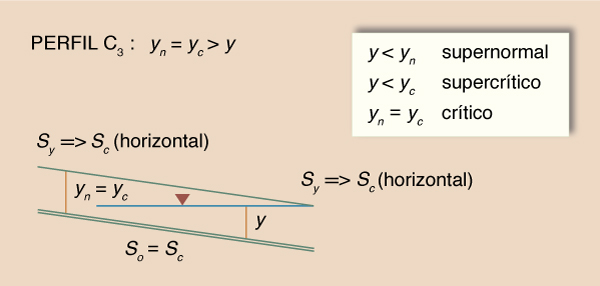
C3: So = Sc
|
Fig. 7-11 Perfil C3 de la superficie del agua.
|
|
El gradiente de profundidad Sy
varía de Sc en el
extremo de aguas abajo, a Sc
en el extremo de aguas
arriba, es decir, el perfil de la superficie del agua
es una línea horizontal.
|
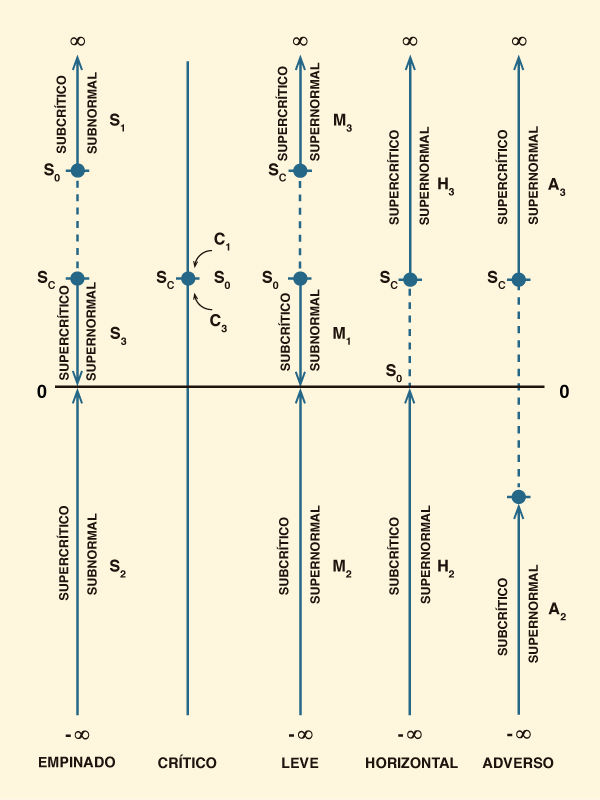
La Figura 7-15 muestra una representación gráfica de los
gradientes de profundidad en los cálculos de perfiles.
Las flechas indican la
dirección de cálculo.
|
Fig. 7-15 Representación gráfica de los rangos del gradiente de
profundidad
en los cálculos de perfiles.
|
|
7.3 LÍMITES DE LOS PERFILES
Los gradientes de profundidad pueden tener
cinco (5) límites (Fig. 7-15):
-
La pendiente
del canal So
-
La pendiente crítica Sc
Cero.
+ ∞
- ∞
Los límites teóricos para los perfiles de la superficie pueden ser analizados usando
la Ec. 7-25, la cual se repite aquí con una pequeña variación:
So - Sc F 2
Sy = ______________
1 - F 2
| (7-46) |
De la Ec. 7-46:
Sy (1 - F 2) = So - Sc F 2
| (7-47) |
So - Sy
F 2 = ____________
Sc - Sy
| (7-48) |
Para el flujo uniforme (normal) Sy = 0,
y la Ec. 7-48 se reduce a:
Para el flujo gradualmente variado:
Sy ≠ 0, y la Ec. 7-48 está
sujeto a tres (3) casos:
-
F 2 > 0
So > Sy y Sc > Sy
Se cumple la siguiente desigualdad: So > Sy < Sc
So < Sy y Sc < Sy
Se cumple la siguiente desigualdad: So < Sy > Sc
-
Se concluye que Sy tiene que ser ya sea menor que ambos So y Sc, o mayor que ambos.
|
F 2 < 0: Dado que F ≥ 0, esta condición es imposible.
La siguiente
desigualdad NO se cumple: So > Sy > Sc
La siguiente desigualdad NO se cumple: So < Sy < Sc
Se concluye que Sy no puede ser menor que So
y mayor que
Sc , o
menor que Sc y mayor que
So
.
Así, Sy tiene que ser menor que ambos So y Sc,
o mayor que ambos (Ver Caso 1).
|
Uso de los perfiles de remanso
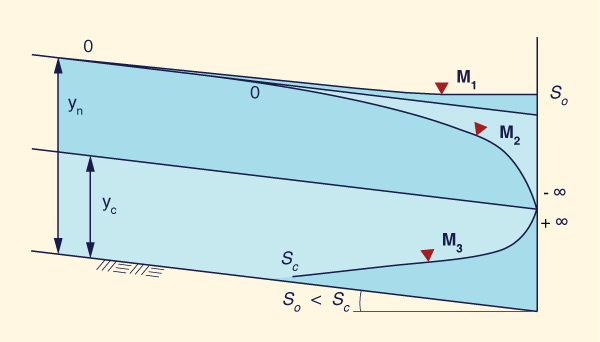
La Tabla 7-3 y la Fig. 7-17 muestran perfiles típicos de remanso y abatimiento en canales de pendiente leve o moderada.
|
Tabla 7-3 Perfiles típicos de remanso y abatimiento en canales de pendiente leve (moderada). |
| M1
|
Flujo en un canal de pendiente leve (o moderada), aguas arriba de un reservorio.
|
| M2
|
Flujo en un canal de pendiente leve (o moderada), aguas arriba de un cambio brusco de nivel o de un canal de pendiente pronunciada con flujo supercrítico.
|
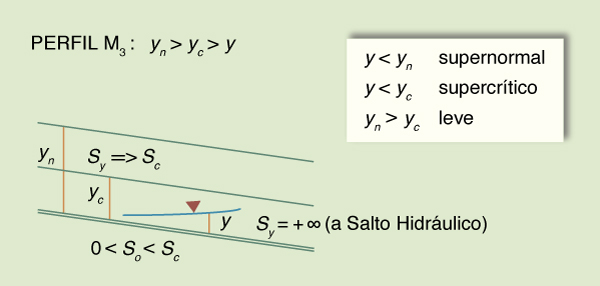
| M3
|
Flujo en un canal de pendiente leve (o moderada), aguas abajo de un canal de pendiente pronunciada
con flujo supercrítico.
|
|
Fig. 7-17 Ejemplos típicos de perfiles leves o moderados.
|
|
La Tabla 7-4 y la Fig. 7-18 muestran perfiles típicos de remanso y abatimiento
en canales de pendiente empinada (o pronunciada).
|
Tabla 7-4 Perfiles típicos de remanso y abatimiento
en canales de pendiente empinada (o pronunciada).
|
| S1
|
Flujo en un canal de pendiente empinada (o pronunciada), aguas arriba de un reservorio.
|
| S2
|
Flujo en un canal de pendiente empinada (o pronunciada), aguas abajo de un canal leve o moderado
con flujo subcrítico.
|
| S3
|
Flujo en un canal de pendiente empinada (o pronunciada), aguas abajo de un canal más
pronunciado con flujo supercrítico.
|
|
Fig. 7-18 Ejemplos típicos de perfiles empinados
o pronunciados.
|
|
7.4 METODOLOGÍAS
Existen dos formas de calcular los perfiles de la superficie de agua:
-
El método
directo.
-
El método estándar.
El método directo es aplicable a canales prismáticos,
mientras que el método estándar es aplicable a
cualquier canal,
prismático o no prismático (Tabla 7-5).
Como su nombre lo indica, el método directo es directo y se puede usar fácilmente con una
hoja de cálculo; además su solución es relativamente sencilla.
El método estándar es iterativo y de solución más compleja.
En la práctica, el método estándar
está representado
por el Hydrologic Engineering Center
River Analysis System, conocido como HEC-RAS (U.S. Army Corps of Engineers, 2014).
El método directo se aplica particularmente cuando los
datos son escasos y los recursos limitados.
Por otro lado, el método
estándar se aplica a los proyectos más detallados.
El uso de un programa ampliamente aceptado como el HEC-RAS
aumenta la credibilidad del método estándar.
En el
método estándar, el número necesario de secciones transversales varía de acuerdo a la pendiente del canal.
Los canales más pronunciados pueden requerir más secciones
transversales.
Una menor variabilidad en las secciones transversales da resultados más confiables.
Cabe notar que las características bidimensionales o tridimensionales del flujo no se pueden representar con precisión
con el modelo unidimensional HEC-RAS.
La Tabla 7-5 muestra una comparación de los métodos directo y estándar.
|
Tabla 7-5 Comparación de los
métodos directo y estándar.
|
| No. | Característica | Método directo |
Método
estándar |
| 1 | Forma de la
sección transversal | Prismática |
Cualquiera
(prismática o no prismática) |
| 2 | Facilidad de cálculo | Fácil (horas) |
Difícil (días) |
| 3 | El cálculo avanza ⇒ | Directamente |
Por
iteración (prueba y error) |
| 4 | Tipo
de la sección transversal | Una sección transversal
típica (prismática) |
Varias secciones transversales (no prismáticas) |
| 5 | Requerimiento de datos | Mínimo |
Extenso | | 6 | La precisión aumenta con ⇒ | Un incremento pequeño de la
profundidad de flujo
|
Un mayor número de secciones transversales y/o
menor variabilidad de la sección transversal |
| 7 | Variable independiente | Profundidad de flujo |
Longitud del canal |
| 8 | Variable dependiente | Longitud del canal |
Profundidad de flujo |
| 9 | Herramientas de cálculo | Hoja de cálculo o programación |
HEC-RAS |
| 10 | Confiabilidad | El resultado siempre es
posible |
El resultado a veces no es
posible, dependiendo del tipo de sección transversal |
| 11 | Costo | Comparativamente pequeño |
Comparativamente grande |
| 12 | Aceptación pública | Media |
Alta |
7.5 EJEMPLO DEL MÉTODO DIRECTO
Cálculo de los perfiles M2 y S2,
aguas arriba y aguas abajo de un cambio de pendiente, de moderada a pronunciada
Datos de entrada:
- Descarga Q = 2000 m3
- Ancho de fondo b = 100 m.
- Talud 2 H : 1 V
- Pendiente del canal aguas arriba = 0.0001
- n de Manning del canal
aguas arriba = 0.025
- Pendiente del canal aguas abajo = 0.03
- n de Manning del canal
aguas abajo = 0.045
Solución
Calcular la profundidad y velocidad normal, y la profundidad
y velocidad crítica, en los canales aguas arriba y aguas abajo.
Utilizar CANAL EN LÍNEA 05.
Para el canal aguas arriba:
Profundidad normal = 10.098 m
Velocidad normal = 1.648 m/s
Número de Froude normal = 0.179
Profundidad crítica = 3.364 m
Velocidad crítica = 5.571 m/s
Para el canal aguas abajo:
Profundidad normal = 2.669 m
Velocidad normal = 7.113 m/s
Número de Froude normal = 1.425
Profundidad crítica = 3.364 m
Velocidad crítica = 5.571 m/s
Cálculo de la
pendiente crítica para el canal aguas arriba:
yc = 3.364 m
Vc = 5.571 m/s
Ac = (b + zyc ) yc = 359.033 m2
P = b + 2 yc (1 + z 2)1/2 = 115.044 m
Rc = Ac / Pc = 3.121 m
Sc = n 2 Vc2 / Rc4/3 = (0.025)2
(5.571)2 (3.121)4/3 = 0.00425
Verificar la pendiente crítica con CANAL EN LÍNEA 04: Sc = 0.004254.
Cálculo de la pendiente crítica para el canal aguas abajo:
Sc = n 2 Vc2 / Rc4/3 = (0.045)2
(5.571)2 (3.121)4/3 = 0.0138
Verificar la pendiente crítica con CANAL EN LÍNEA 04: Sc = 0.01378.
El cálculo del perfil M2 se muestra
en la Tabla 7-6.
Se detalla lo siguiente:
El cálculo procede en la dirección aguas arriba, a partir de la profundidad crítica en el extremo de aguas abajo.
Columna [1]:
La segunda profundidad se establece en 4 m; para las siguientes profundidades el intervalo se toma en 1 m.
Columna [2]: El área de flujo: A = (b + zy ) y . . . (1)
Columna [3]: La velocidad media: V = Q / A . . . (2)
Columna [4]: La carga de velocidad: V 2 / (2g) . . . (3)
Columna [5]: La carga específica: H = y + V 2 / (2g) . . . (4)
Columna [6]: El perímetro mojado: P = b + 2 y (1 + z 2)1/2 . . . (5)
Columna [7]: El radio hidráulico: R = A / P . . . (6)
Columna [8]: La pendiente de fricción: Sf = n 2 V 2 / R 4/3 . . . (7)
Columna [9]: La pendiente de fricción promedio: Sf ave = 0.5 (Sf 1
+ Sf 2) . . . (8)
Columna [10]: La diferencia de carga específica: ΔH = H2 - H1 . . . (9)
Columna [11]:
El incremento de longitud del canal ΔL, el cual se explica en el recuadro de abajo.
Columna [12]: La longitud acumulada, es decir, la suma acumulada de ΔL.
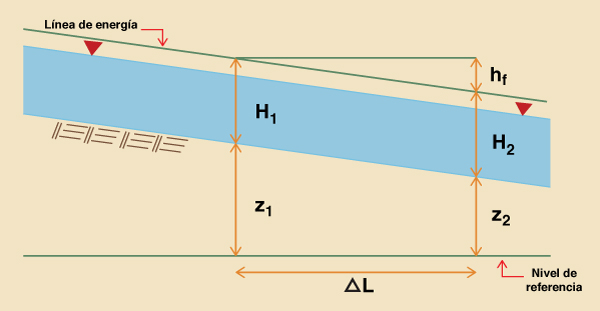
Derivación de la fórmula para el incremento de longitud del canal ΔL
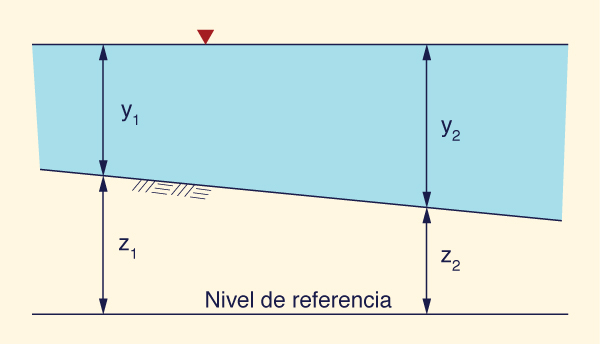
Con referencia a la Fig. 7-19, la pendiente de fricción media es:
hf
Sf ave = ______
ΔL
| (7-54) |
|
Fig. 7-19 Ilustración del
cálculo del incremento de longitud del canal ΔL.
|
|
H1 +
z1 = H2 +
z2 + Sf ave ΔL
| (7-55) |
z1 -
z2 = H2 -
H1 + Sf ave ΔL
| (7-56) |
z1 -
z2 - Sf ave ΔL = H2 -
H1
| (7-57) |
z1 -
z2
So = _________
ΔL
| (7-58) |
So ΔL - Sf ave ΔL = H2 -
H1
| (7-59) |
(So - Sf ave) ΔL = H2 -
H1
| (7-60) |
H2 -
H1
ΔL = ______________
So - Sf ave
| (7-61) |
ΔH
ΔL = ______________
So - Sf ave
| (7-62) |
La ecuación 7-62 permite el cálculo del incremento de longitud
del canal ΔL, es decir, la Col. 11 de la Tabla 7-6.
Cuando ΔL es negativa, el cálculo procede
aguas arriba, como en el perfil M2 (Tabla 7-6).
Contrariamente, cuando ΔL es positivo, el cálculo procede
aguas abajo, como en el perfil S2 (Tabla 7-7).
|
|
Tabla 7-6 Cálculo del perfil M2 de la superficie del agua (So = 0.0001). |
| [1]
| [2]
| [3]
| [4]
| [5]
| [6]
| [7]
| [8]
| [9]
| [10]
| [11]
| [12]
|
| y
| A
| V
| V 2/(2g )
| H
| P
| R
| Sf
| Sf ave
| ΔH
| ΔL
| ∑ ΔL
|
|
| (1)
| (2)
| (3)
| (4)
| (5)
| (6)
| (7)
| (8)
| (9)
| Recuadro
|
|
| 3.364
| 359.033
| 5.570
| 1.581
| 4.945
| 115.044
| 3.1208
| 0.00425
| ---
| ---
| ---
| 0
|
| 4.000
| 432.000
| 4.630
| 1.092
| 5.092
| 117.888
| 3.664
| 0.00237
| 0.00331
| 0.147
| -45.794
| -45.794
|
| 5.000
| 550.000
| 3.636
| 0.674
| 5.674
| 122.360
| 4.495
| 0.00111
| 0.00174
| 0.528
| -354.878
| -400.672
|
| 6.000
| 672.000
| 2.976
| 0.451
| 6.451
| 126.833
| 5.298
| 0.00060
| 0.000855
| 0.777
| -1029.139
| -1429.811
|
| 7.000
|
|
|
|
|
|
|
|
|
|
|
|
| 8.000
|
|
|
|
|
|
|
|
|
|
|
|
| 9.000
|
|
|
|
|
|
|
|
|
|
|
|
| 10.000
|
|
|
|
|
|
|
|
|
|
|
|
| 10.097
|
|
|
|
|
|
| 0.0001
|
|
|
|
|
En el método directo, la exactitud del cálculo depende
del tamaño del intervalo de profundidad (Col. [1] de
la Tabla 7-6).
Cuanto menor sea el intervalo, más preciso será el cálculo.
Esto de debe a que el promedio de la pendiente de fricción para un
subtramo (Col. [9]) es la media aritmética de las pendientes de
fricción en los dos puntos adyacentes.
En la práctica, el cálculo utilizando una computadora usaría
un intervalo más preciso que el que se muestra en la Tabla 7-6.
El cálculo del perfil de la superficie del agua S2
se muestra en la Tabla 7-7.
|
Tabla 7-7 Cálculo
del perfil de la superficie del agua S2 (So = 0.03). |
| [1]
| [2]
| [3]
| [4]
| [5]
| [6]
| [7]
| [8]
| [9]
| [10]
| [11]
| [12]
|
| y
| A
| V
| V 2/(2g )
| H
| P
| R
| Sf
| Sf ave
| ΔH
| ΔL
| ∑ ΔL
|
|
| (1)
| (2)
| (3)
| (4)
| (5)
| (6)
| (7)
| (8)
| (9)
| Recuadro
|
|
| 3.364
| 359.033
| 5.570
| 1.581
| 4.945
| 115.044
| 3.1208
| 0.00425
| ---
| ---
| ---
| 0
|
| 3.300
| 351.780
| 5.685
| 1.647
| 4.9475
| 114.758
| 3.0654
| 0.0147
| 0.01425
| 0.002
| 0.127
| 0.127
|
| 3.200
| 340.48
| 5.874
| 1.759
| 4.9586
| 114.311
| 2.979
| 0.0163
| 0.0155
| 0.0111
| 0.765
| 0.892
|
| 3.100
| 329.22
| 6.075
| 1.881
| 4.981
| 113.864
| 2.891
| 0.0181
| 0.0172
| 0.0224
| 1.750
| 2.642
|
| 3.000
|
|
|
|
|
|
|
|
|
|
|
|
| 2.900
|
|
|
|
|
|
|
|
|
|
|
|
| 2.800
|
|
|
|
|
|
|
|
|
|
|
|
| 2.700
|
|
|
|
|
|
|
|
|
|
|
|
| 2.669
|
|
|
|
|
|
| 0.03
|
|
|
|
|
Cálculos en línea
Los perfiles M2 se pueden calcular en línea usando ONLINE_WSPROFILES_22 (Fig. 7-20).
Usando el número de intervalos computacionales n = 100,
y el número de intervalos tabulares de salida m = 100, la longitud del perfil M2 es: ∑ ΔL = 147,691.5 m.
|
Fig. 7-20 Perfil M2 de la superficie del agua .
|
|
El perfil S2 se puede calcular en
línea usando ONLINE_WSPROFILES_25 (Fig. 7-21).
Usando el número
de intervalos computacionales n = 100, y el número de intervalos
tabulares de salida m = 100, la longitud del perfil S2 es: ∑ ΔL = 152.02 m.
|
Fig. 7-21 Perfil S2 de la superficie del agua.
|
|
PREGUNTAS
-
¿Cómo se define el flujo permanente gradualmente variado?
-
¿Cómo se define el flujo retardado?
-
¿Cómo se define el flujo acelerado?
-
¿Cómo se define el flujo subnormal?
-
¿Cómo se define el flujo supernormal?
-
¿Cuántos perfiles existen en el
flujo permanente gradualmente variado?
-
¿Cuál es la regla para la familia Tipo I de los perfiles de la superficie del agua?
-
¿Cuál es la regla para la familia Tipo
III de los perfiles de la superficie del agua?
-
¿Cuáles perfiles de la superficie del agua son totalmente horizontales?
-
¿Cuáles son los cinco límites a los cuales tienden los perfiles?
-
¿Cuál es la aplicación
típica del perfil M1?
-
¿Cuál es la aplicación
típica del perfil S1?
-
¿Cuál es la aplicación
típica del perfil S3?
-
¿Cuál es la diferencia principal entre los métodos directo
y estándar para el cálculo de los perfiles de la superficie del agua?
PROBLEMAS
-
Un río tiene las siguientes propiedades: descarga Q = 30 m3/s,
ancho de fondo b = 55 m, talud z = 2,
pendiente de fondo So = 0.0004, y n de Manning = 0.035.
Se propone construir una presa de derivación de 2 metros de altura sobre el río
para elevar la carga para un canal de riego (Fig. 7-22).
-
Calcular la profundidad normal.
-
Calcular la longitud total del perfil de la superficie del agua M1.
Usar n = 400 y m = 400.
-
Calcular la longitud parcial del perfil M1, desde la presa hasta una ubicación
aguas arriba donde la profundidad normal sea excedida en 1%.
Usar CANAL EN LÍNEA 01
y EN LÍNEA CURVA REMANSO 21.
|
Fig. 7-22 Una presa de derivación.
|
|
-
Un río tiene las siguientes propiedades: descarga
Q = 1000 pies3/s, ancho del fondo b = 150 pies,
talud z = 2, pendiente de fondo So = 0.00038, y n de Manning = 0.035.
Se proyecta una presa de derivación de 6 pies de altura, para elevar la carga para un canal de riego.
-
Calcular la profundidad normal.
Calcular la longitud total del perfil de la superficie del agua
M1. Usar n = 400 y m = 400.
-
Calcular la longitud parcial del perfil M1, desde la presa
hasta una ubicación aguas arriba donde la profundidad normal sea excedida
en 1%.
Usar CANAL EN LÍNEA 01
y EN LÍNEA CURVA REMANSO 21.
-
Un río de pendiente moderada fluye hacia un río de pendiente pronunciada, produciendo un perfil M2
aguas arriba del borde. Las condiciones
hidráulicas en el canal son: Q = 28 m3/s,
ancho de fondo b = 12 m, talud z = 2.5,
pendiente del fondo So = 0.0007,
y n de Manning = 0.04. Asumir la profundidad crítica cerca del
cambio de pendiente.
-
Calcular las profundidades crítica y normal.
-
Calcular la longitud M2 del perfil de la superficie del agua
usando n = 100 y m = 100.
-
Calcular la longitud M2 del perfil de la superficie del agua
usando n = 200 y m = 200.
-
Calcular la longitud M2 del perfil de la superficie del agua
usando n = 400 y m = 400.
-
Comentar los resultados de los incisos b, c, y d.
-
Determinar la longitud de diseño del canal a 99% de la
profundidad normal. Usar n = 400.
Usar CANAL EN LÍNEA 05
y EN LÍNEA CURVA REMANSO 22.
-
Un río de pendiente moderada fluye hacia un río de pendiente pronunciada, produciendo un perfil M2
aguas arriba del borde. Las condiciones hidráulicas
en el canal son: Q = 500 pies3/s, ancho del fondo b = 30 pies,
pendiente lateral z = 1.5,
pendiente del fondo So = 0.00075, y n de Manning = 0.04.
Asumir la profundidad crítica cerca al cambio en la pendiente.
-
Calcular las profundidades crítica y normal.
-
Calcular la longitud del perfil de la superficie del agua M2
usando n = 100 y m = 100.
-
Calcular la longitud del perfil de la superficie del agua M2
usando n = 200 y m = 200.
-
Calcular la longitud del perfil de la superficie del agua M2
usando n = 400 y m = 400.
-
Comentar sobre los resultados de b, c, y d.
-
Determinar la longitud de diseño del canal a 99% de la
profundidad normal. Usar n = 400.
Usar CANAL EN LÍNEA 05
y EN LÍNEA CURVA REMANSO 22.
-
El flujo a través de un vertedero discurre hacia un canal de pendiente leve, produciendo un salto hidráulico. El canal es rectangular, con
Q = 3 m3/s, ancho de fondo b = 8 m, y n
de Manning = 0.015.
La profundidad y la pendiente en el pie del vertedero son 0.1 m y 0.1, respectivamente.
La pendiente del canal aguas abajo, el cual funciona
como una poza de disipación, es 0.0001. Calcular:
-
La profundidad crítica.
-
La longitud Ltc desde el pie del vertedero
hasta la profundidad crítica aguas abajo.
-
El número de Froude en el pie del vertedero.
-
El número de Froude aguas abajo del salto hidráulico.
-
La profundidad secuente y2 (la profundidad normal
aguas abajo del salto hidráulico),
-
La longitud Lj del salto, asumiendo Lj = 6.2 y2
-
La longitud mínima de la poza de disipación:
Lsb = Ltc + Lj
Usar CANAL EN LÍNEA 02
y EN LÍNEA CURVA REMANSO 23. En este último, usar n = 100 y m = 100.
El flujo a través de un vertedero discurre hacia un canal de pendiente leve, produciendo un salto hidráulico. El canal es rectangular, con
Q = 100 pies3/s, ancho de fondo b = 20 pies, y n
de Manning = 0.015.
La profundidad y la pendiente en el pie del vertedero son 0.4 pies y 0.1, respectivamente.
La pendiente del canal aguas abajo, el cual funciona
como una poza de disipación, es 0.0001. Calcular:
-
La profundidad crítica.
-
La longitud Ltc desde el pie del vertedero
hasta la profundidad crítica aguas abajo.
-
El número de Froude en el pie del vertedero.
-
El número de Froude aguas abajo del salto hidráulico.
-
La profundidad secuente y2 (la profundidad normal
aguas abajo del salto hidráulico).
-
La longitud Lj del salto, asumiendo Lj = 6.2 y2
-
La longitud mínima de la poza de disipación:
Lsb = Ltc + Lj
Usar CANAL EN LÍNEA 02
y EN LÍNEA CURVA REMANSO 23. En este último, usar n = 100 y m = 100.
-
Una presa de derivación de altura H = 1.8 m está proyectada en un río de pendiente pronunciada con So = 0.035.
Se prevé un salto hidráulico aguas arriba de la presa.
Identificar el tipo de perfil de la superficie del agua.
Usando CALCULADORA EN
LÍNEA, calcular la longitud del perfil de la
superficie del agua, desde la ubicación de la presa de
derivación, en la dirección aguas arriba, al
[extremo aguas abajo del] salto hidráulico.
El canal tiene Q = 4 m3/s, ancho de fondo b = 3 m,
talud z = 1,
y n de Manning = 0.03.
¿Cuáles son las profundidades secuentes?
¿Cuál es el número de Froude del flujo aguas arriba?
Usar m = 100 y n = 100.
Verificar la profundidad secuente y2
usando CANAL EN LÍNEA 11.
-
Un canal de pendiente moderada fluye hacia un canal de pendiente pronunciada con
So = 0.03.
Identificar el tipo de perfil de la superficie del agua
en el canal de pendiente pronunciada.
Usando CALCULADORA EN LÍNEA, calcular la
profundidad normal en el canal de pendiente pronunciada, y la longitud
del perfil de la superficie del agua hasta que la profundidad esté dentro del 2% de la profundidad normal.
El canal tiene Q = 3 m3/s, ancho del fondo b = 5 m,
talud z = 0,
y n de Manning = 0.015.
¿Cuál es el número de Froude a la profundidad normal en
el canal de pendiente pronunciada? Usar m = 100 y n = 100.
-
Un canal de pendiente pronunciada So = 0.035
fluye hacia un canal con pendiente más suave
So = 0.012.
Identificar el tipo de perfil de la superficie del agua en el canal de pendiente suave.
Usando CALCULADORA EN LÍNEA, calcular la profundidad normal en el canal aguas abajo, y la longitud
[a profundidad normal] del perfil de la superficie del agua.
El canal tiene Q = 3.2 m3/s, ancho de fondo b = 4 m, talud z = 2,
y n de Manning = 0.015.
¿Cuáles son los números de Froude a la profundidad normal?
¿Cuál es la profundidad normal en el canal aguas arriba?
¿Cuál sería la longitud del perfil
en caso de que el n de Manning se estime en 0.013? Usar m = 100 y n = 100.
-
Un río tiene las siguientes propiedades:
descarga
Q = 15 m3/s, ancho de fondo b = 8 m,
talud z = 2,
pendiente de fondo So = 0.0025, y n de Manning = 0.035.
Se proyecta una presa de derivación de 2 m de altura para elevar la carga para un canal de riego (Fig. 7-23).
-
Calcular la profundidad normal.
-
Calcular la longitud total del perfil de la superficie del agua
M1. Utilizar tres casos: (a) n = 100 y m = 100, (b) n = 200 y m = 200,
y (c) n = 400 y m = 400.
Comentar los resultados.
-
Usando los resultados de mayor resolución (n = 400 y m = 400), calcular la
longitud parcial del perfil M1,
desde la ubicación de la presa hasta un punto aguas arriba donde la profundidad normal sea excedida por 1%.
Usar CANAL EN LÍNEA 01
y EN LÍNEA CURVA REMANSO 21.
|
Fig. 7-23 Una presa de derivación.
|
|
-
Un flujo a través de un vertedero discurre hacia un canal de pendiente leve, produciendo un salto hidráulico.
El canal es rectangular, con
Q = 3.6 m3/s, ancho de fondo b = 5 m, y n de
Manning = 0.015.
La profundidad de flujo
y la pendiente del canal en el pie del vertedero son 0.15 m y 0.1, respectivamente.
La pendiente del canal aguas abajo, el cual funciona como
una poza de disipación, es 0.00016. Utilizar n = 100 y
m = 100. Calcular:
-
La profundidad crítica.
-
La longitud Ltc desde el pie del vertedero
hasta la profundidad crítica aguas abajo.
-
El número de Froude en la punta del vertedero.
-
El número de Froude aguas abajo del salto hidráulico.
-
La profundidad secuente y2 (la profundidad normal
aguas abajo del salto hidráulico).
-
La longitud Lj del salto, asumiendo
Lj = 6.2 y2
-
La longitud mínima de la poza de disipación:
Lsb = Ltc + Lj
¿Cuál sería la longitud de la poza de disipación si el ancho de fondo se aumentara a 7 m?
Usar CANAL EN LÍNEA 02
y ONLINE WSPROFILES 23.
En la última, usar n = 100 y m = 100.
-
Una presa de derivación de 5 m de altura se proyecta en un canal que funciona bajo flujo crítico.
El canal es rectangular, con Q = 100 m3/s, ancho de fondo b = 4.7 m,
pendiente de fondo So = 0.01, y n de Manning = 0.023.
Calcular la longitud del perfil
C1. Asumir n = 100 y m = 100.
-
Un canal de pendiente pronunciada, con
So = 0.03, fluye hacia un canal que funciona bajo
flujo crítico.
El canal es rectangular, con
Q = 100 m3/s, ancho de fondo b = 4.7 m,
pendiente de fondo So = 0.01, y n de Manning = 0.024. Calcular la longitud del perfil
C3. Asumir n = 100 y m = 100.
-
Un canal horizontal de longitud L = 500 m es diseñado
para conducir Q = 5 m3/s desde un reservorio aguas arriba
hasta una caída libre aguas abajo. El ancho de fondo es
b = 2 m y el talud z = 1.5.
El canal está revestido con gaviones y el n de Manning recomendado por el fabricante es n = 0.028.
-
¿Cuál es la profundidad de flujo aguas arriba (con precisión de 1 cm) requerida para pasar la descarga de diseño?
¿Cuál es la profundidad de flujo aguas abajo, es decir,
la profundidad crítica en la caída?
Usar EN LÍNEA CURVA REMANSO 32. Suponer n = 100 y m = 100.
-
Una compuerta está diseñada para liberar el flujo
supercrítico hacia una poza de disipación, donde se producirá
un salto hidráulico.
El fondo del canal es horizontal, de sección transversal rectangular. La descarga de diseño es Q = 5 m3/s,
el ancho de fondo b = 5 m, y el n de Manning = 0.015.
Usar
EN LÍNEA CURVA REMANSO 35. Suponer que n = 100 y m = 100.
Suponer que So,u/s = 0.05 de manera que el flujo a través de la compuerta permanezca supercrítico.
BIBLIOGRAFÍA
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, Nueva York.
U.S. Army Corps of Engineers. (2014). HEC-RAS: Hydrologic Engineering Center River Analysis System.
USDA Soil Conservation Service. (1971). Classification system for varied flow in prismatic channels. Technical Release No. 47 (TR-47), Washington, D.C.
| http://openchannelhydraulics.sdsu.edu |
|
150815 19:00 |
| |
|