Convergencia de modelos implícitos de cuatro puntos de flujo no permanente en canales, Dr. Victor M. Ponce.

Convergencia de modelos
implícitos de cuatro puntos
de flujo no permanente en canales

Victor M. Ponce, M. ASCE, Horst Indlekofer, y Daryl B. Simons, F. ASCE
Versión online 2019

[Versión original 1978]

1. INTRODUCCIÓN

La solución numérica de las ecuaciones de flujo no permanente en canales (ecuaciones de Saint Venant) es un tema establecido en la literatura de ingeniería hidráulica. Generalmente se prefieren los esquemas numéricos implícitos a los esquemas explícitos (9), porque permiten pasos de tiempo más grandes y, por lo tanto, reducen el esfuerzo computacional. Entre los esquemas implícitos, el esquema de cuatro puntos, también conocido como esquema de Preissmann (2, 5), ha recibido una amplia atención. Sin embargo, las propiedades de estabilidad y convergencia de este esquema aún no están claramente definidas.

Las ecuaciones de Saint Venant constituyen un conjunto de ecuaciones diferenciales parciales cuasilineales. En la actualidad, no existe un método para analizar la estabilidad y convergencia de soluciones numéricas de ecuaciones de este tipo. Por otro lado, existen varios métodos para analizar la estabilidad y convergencia de ecuaciones diferenciales parciales lineales (11), entre ellos, en particular, el enfoque heurístico de Von Neumann (7). Tradicionalmente, una salida a la dificultad matemática impuesta por la naturaleza cuasilineal de las ecuaciones de Saint Venant ha sido linealizarlas, asumiendo que el comportamiento del sistema lineal se aproxima al comportamiento más complejo del sistema cuasilineal. En la práctica, el análisis lineal sirve, si no como cuantitativo, al menos como una descripción cualitativa de los fenómenos no lineales.

2. ESTABILIDAD Y CONVERGENCIA

La característica esencial de un modelo numérico es la sustitución de una derivada tal como ∂ƒ/∂s por una relación de diferencias finitas tal como Δƒ/Δs. Al hacerlo, el modelo numérico debe satisfacer ciertos requisitos de estabilidad y convergencia. La estabilidad se refiere a la capacidad del esquema numérico de marchar en el tiempo sin generar una amplificación del error. La convergencia se refiere a la capacidad del esquema para reproducir los términos de la ecuación diferencial con suficiente precisión. La estabilidad, en el sentido de O'Brien et al. (7), está controlada por errores de redondeo; de otro modo la convergencia está controlada por errores de discretización. En general, la estabilidad se ve afectada si la discretización se hace más fina, mientras que lo contrario sucede desde el punto de vista de la convergencia.

En la práctica, la estabilidad es una condición necesaria para el funcionamiento del modelo, ya que un modelo inestable tiene poca o ninguna utilidad. En los modelos implícitos, la estabilidad generalmente se logra a expensas de la convergencia. Por lo tanto, la convergencia es el tema central: Una vez que se demuestre que el modelo es estable, es necesario evaluar sus propiedades de convergencia.

Las propiedades numéricas de los esquemas implícitos de cuatro puntos han sido estudiadas por Liggett y Cunge (5), y Fread (3). Liggett y Cunge utilizaron un sistema simple de ecuaciones diferenciales parciales lineales para derivar conclusiones sobre las propiedades numéricas del esquema implícito de cuatro puntos. Si bien se dieron cuenta plenamente de las limitaciones de su análisis, señalaron, no obstante, que se esperaría que las ecuaciones de Saint Venant se comportaran de manera similar. Los cálculos reales han demostrado, sin embargo, que el valor "teóricamente más preciso" del factor de ponderación, θ = 0.5, no es práctico desde el punto de vista de la estabilidad. En la práctica puede ser necesario un valor de θ ≥ 0.6 (2).

Fread (3) ha analizado las propiedades numéricas del esquema implícito de cuatro puntos. Fread usó una versión linealizada de las ecuaciones de Saint Venant, pero simplificó la ecuación de movimiento despreciando los términos de inercia convectiva y la pendiente de fondo, y en la ecuación de continuidad, despreciando el término de almacenamiento de cuña. El análisis lineal completo ha sido posible gracias a Ponce y Simons (8), quienes formularon la solución analítica para la propagación de perturbaciones sinusoidales en el flujo de canales sobre la base de una versión linealizada de las ecuaciones de Saint Venant (6).

El presente trabajo tiene como objetivo determinar las propiedades de convergencia de los modelos numéricos implícitos de cuatro puntos del flujo no permanente en canales. Usando el método de Von Neumann, se comparan la celeridad y atenuación de la solución numérica con las de la solución analítica (8,7,11). Las conclusiones se refieren a la evaluación de la convergencia en función de parámetros físicos y numéricos.

3. ECUACIONES DE GOBIERNO

El flujo no permanente unidimensional en canales, por unidad de ancho, se puede expresar mediante un conjunto de las siguientes ecuaciones diferenciales parciales (4):

Ecuación de continuidad:

∂d ∂u ∂d
^____ + d ^____ + u ^____ = 0
∂t ∂x ∂x (1)

Ecuación de movimiento:

1 ∂u u ∂u ∂d
^____ ^_____ + ^____ ^_____ + ^_____ + (S_f - S_o ) = 0
g ∂t g ∂x ∂x
(2)

en las cuales u = velocidad media; d = profundidad de flujo; g = aceleración de la gravedad; S_ƒ = pendiente de fricción; S_o = pendiente de fondo; x = variable espacial; y t = variable temporal.

Las Ecuaciones 1 y 2 deben satisfacer el flujo no perturbado (equilibrio o flujo uniforme permanente) para el cual u = u_o, y d = d_o, así como el flujo perturbado para el cual u = u_o + u', y d = d_o + d'. Los términos con un superíndice representan pequeñas perturbaciones (componentes de flujo no permanente) al flujo uniforme. Ingresando las variables perturbadas en las Ecs. 1 y 2, después de la linealización, despreciando los términos de segundo orden, se obtiene (6):

  ∂d'             ∂u'              ∂d'
^____ + d_o ^_____ + u_o ^_____ = 0
  ∂t               ∂x               ∂x (3)

  1       ∂u'          u_o      ∂u'           ∂d'                    u'         d'
^____ ^_____ + ^____ ^_____ + ^_____ + S_o ( 2 ^____ - ^____ ) = 0
  g       ∂t            g       ∂x            ∂x                     u_o        d_o
(4)

4. SOLUCIÓN ANALÍTICA

Ponce y Simons han demostrado (8) que la solución analítica de las Ecs. 3 y 4 se caracteriza por la celeridad de propagación y la atenuación de las perturbaciones sinusoidales. Para la celeridad, eligieron la celeridad adimensional c_{_*} definida como sigue:

                         L
                     (^____ )
           c            T
c_{_*} = ^____  =  ^_______
          u_o           u_o
(5)

en la cual L = longitud de onda de la perturbación sinusoidal; y T = período de la onda. Para la atenuación, eligieron el decremento logarítmico δ definido de la siguiente forma:

a_t_{_o}₊_T = a_t_{_o}e^{^δ} (6)

en la cual a_t_{_o} and a_t_{_o}₊_T son las amplitudes de onda al principio y al final de un período T.

Ambos c_{_*} y δ son funciones del número de Froude del flujo de equilibrio F_o y el número de onda adimensional σ_{_*}, en el cual F_o = u_o / ( gd_o )^1/2 y σ_{_*} = (2π/L) d_o /S_o (Apéndice I).

5. SOLUCIÓN NUMÉRICA

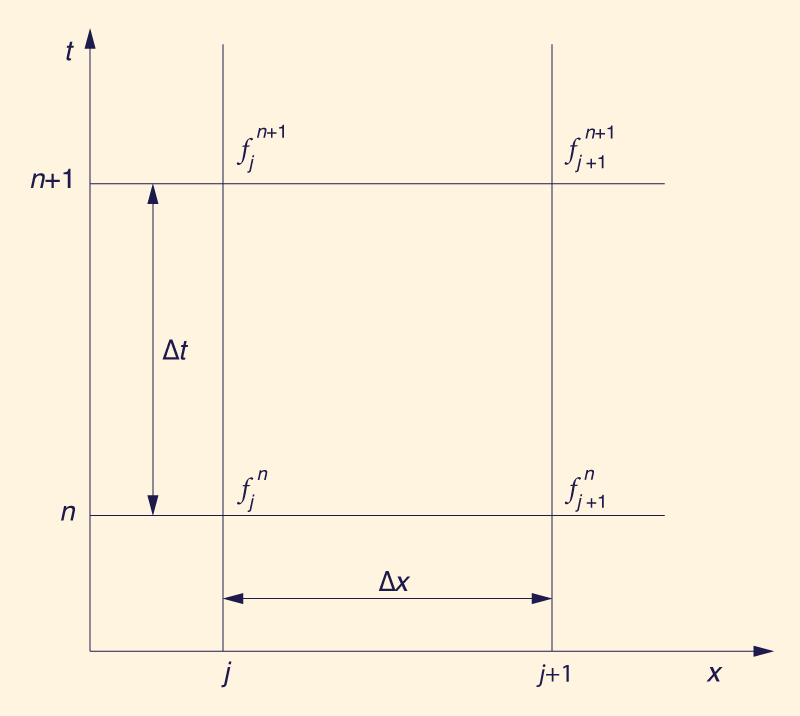
El esquema implícito de cuatro puntos se basa en las siguientes fórmulas (5), Fig.1:

Fig. 1 Definición del esquema implícito de cuatro puntos.

θ (1 - θ)
ƒ (x,t ) = ^___ ( ƒ_j+1 ^{n + 1} + ƒ_j ^{n + 1} ) + ^_______ ( ƒ_j+1ⁿ + ƒ_j ⁿ )
2 2

(7)

∂ 1
^_____ ƒ (x,t ) = ^_____ ( ƒ_j+1 ^{n + 1} - ƒ_{j + 1}ⁿ + ƒ_j ⁿ⁺¹ - ƒ_j ⁿ )
∂t 2∆t

(8)

∂ θ 1 - θ
^_____ ƒ (x,t ) = ^_____ ( ƒ_j+1 ^{n + 1} - ƒ_j ⁿ⁺¹ ) + ^______ ( ƒ_j+1 ⁿ - ƒ_j ⁿ )
∂x ∆x Δx

(9)

en las cuales ƒ(x,t) es una variable dependiente; Δx y Δt son los incrementos de espacio y tiempo, respectivamente; y θ es el factor de ponderación del esquema implícito. El factor de ponderación θ se ingresa en la función y su derivada espacial para permitir una mayor flexibilidad en el funcionamiento actual del modelo. Mientras que el rango estable es 0.5 ≤ θ ≤ 1.0, un rango fuertemente estable es 0.6 ≤ θ ≤ 1.0.

La sustitución de las Ecuaciones 7 y 9 en las Ecs. 3 y 4 conduce a las ecuaciones discretizadas en u' y d'. La solución se postula en la siguiente forma exponencial:

u'
^____ = u_{_*} exp {i (σ_{_*} x_{_*} - β_{_*} t_{_*} )}
u_o (10)

d'
^____ = d_{_*} exp {i (σ_{_*} x_{_*} - β_{_*} t_{_*} )}
d_o (11)

en las cuales x_{_*} = xS_o /d_o; t_{_*} = tu_oS_o /d_o y β_{_*}_R = 2πd_o /Tu_oS_o, y u_{_*} y d_{_*} son funciones de amplitud adimensionales.

La sustitución de las Ecs. 10 y 11 en las ecuaciones discretizadas en u' y d' conduce a lo siguiente:

Δt_{_*} Δt_{_*} ξ
u_{_*} [ i ^_____ (θξ + 1) tan α ] + d_{_*} [ i ^_____ (θξ + 1) tan α + ^____ ] = 0
Δx_{_*} Δx_{_*} 2 (12)

                ξ                   Δt_{_*}
u_{_*} [ F_o^² ^_____ + i F_o^² ^______ (θξ + 1) tan α + Δt_{_*} (θξ + 1) ]
                2                  Δx_{_*}
              Δt_{_*}                               Δt_{_*}
+ d_{_*} [ i ^______ (θξ + 1) tan α - ^_____ (θξ + 1) ] = 0
              Δx_{_*}                               2
(13)

en las cuales i = √-1; ξ = [exp (-iβ_{_*} Δt_{_*}) - 1 ]; α = σ_{_*}Δx_{_*} /2; Δt_{_*} = Δt u_o/ (d_o /S_o); y Δx_{_*} = Δx / (d_o /S_o).

Las Ecuaciones 12 y 13 constituyen un conjunto de dos ecuaciones homogéneas en u_{_*} y d_{_*}. Para que la solución no sea trivial, el determinante de la matriz de coeficientes debe ser nulo. En consecuencia:

                                    C                                         C           α          ξ^² F_o^²
[ (θξ + 1)^² (1 - F_o^²) ( ^____ ) ^² tan^²α + ξ (θξ + 1) ( ^____ ) ( ^____ ) + ^_______ ]
                                    c_{_*}                                         c_{_*}          σ_{_*}             4
                                           C                               C             α
+ i tanα [ ξ (θξ + 1) F_o^² ( ^____ ) + 3 (θξ + 1)^² ( ^____ ) ^² ( ^____ ) ] = 0
                                           c_{_*}                               c_{_*}             σ_{_*}
(14)

en la cual C /c_{_*} = Δt_{_*} /Δx_{_*}. El valor de C se conoce como el número de Courant, y se define como la relación entre la celeridad física c, y la "celeridad de la malla" Δx/Δt. La Ecuación 14 es una ecuación cuadrática compleja en ξ. Puede simplificarse a lo siguiente:

ξ² (M₂ + iN₂) + ξ (M₁ + iN₁) + (M_o + iN_o) = 0 (15)

en la cual:

M_o = (1 - F_o²)P² (16)

N_o = 3PQ (17)

M₁ = 2θM_o + Q (18)

N₁ = F_o^²P + 2θN_o (19)

F_o^²
M₂ = ^_____ + θQ + θ^²M_o
4 (20)

N₂ = θF_o^²P + θ^²N_o (21)

C
P = ( ^____ ) tanα
c_{_*} (22)

C α
Q = ( ^____ ) ( ^____ )
c_{_*} σ_{_*} (23)

Llamando:

A = Q^² - P^² F_o^² (24)

B = -PQ F_o^² (25)

C = (A^² + B^²)^{^1/2} (26)

A + C
D = ( ^________ ) ^{^1/2}
2 (27)

A - C
E = ( ^________ ) ^{^1/2}
2 (28)

y resolviendo la ecuación cuadrática (Ec. 15), las dos raíces son:

ξ_{_1,2} = M + iN (29)

en la cual:

-M₂ ( M₁ ± E ) + N₂ ( -N₁ ± D )
M = ( ^{_______________________________} )
2( M_₂^² + N_₂^² ) (30)

M₂ ( -N₁ ± D ) + N₂ ( M₁ ± E )
N = ( ^{_______________________________} )
2( M_₂^² + N_₂^² ) (31)

Dado que ξ = [exp ( -i β_{_*} Δt_{_*} ) - 1], resulta que:

N
( β_{_*}_R Δt_{_*} ) = - ^________
1 + M (32)

exp ( β_{_*}_I Δt_{_*} ) = [( 1+ M )^² + N ^² ]^{^1/2} (33)

La celeridad adimensional de la solución numérica c_{_*}_n se define como sigue (8):

β_{_*}_R 1 -N
c_{_*}_n = ^_______ = ^________ tan ^-1 ( ^_________ )
σ_{_*} σ_{_*} Δt_{_*} 1 + M (34)

lo cual se reduce a:

                     1                            -N
c_{_*}_n = ^{_____________} tan ^-1 ( ^_________ )
                      C                         1 + M
            2α ( ^_____ )
                      c_{_*} (35)

El decremento logarítmico de la solución numérica δ_n se define como sigue (8):

                  β_{_*}_I           π ln [( 1 + M )² + N ²]
δ_n = 2π ^______ = ^{_______________________}
                 β_{_*}_R                              -N
                                   tan ^-1 ( ^_________ )
                                                  1 + M (36)

Dado que c_{_*} es una función de F_o y σ_{_*}, y M y N son funciones de F_o, σ_{_*}, α, C, y θ, resulta que c_{_*}_n y δ_n son funciones de F_o, σ_{_*}, α, C y θ. F_o y σ_{_*} son los parámetros físicos, siendo F_o = número de Froude y σ_{_*} = número de onda adimensional σ_{_*} = (2π/L) d_o /S_o. Los valores de α, C, y θ son los parámeros numéricos, en los cuales α es la resolución espacial α = π /(L /Δx); C es el número de Courant C = c / (Δx / Δt); y θ es el factor de ponderación del esquema implícito.

6. ANÁLISIS DE CONVERGENCIA

El análisis de convergencia se basa en las siguientes relaciones:

R₁ = exp ( δ_n - δ ) (37)

c_{_*}_n
R₂ = ^______
c_{_*} (38)

El valor R₁ es la relación de atenuación, y R₂ es la relación de translación. Para R₁ > 1, la atenuación numérica es menor que la atenuación física; para R₁ < 1, la atenuación numérica es mayor que la atenuación física. Para R₂ > 1, la translación numérica es mayor que la translación física, y para R₂ < 1, la translación numérica es menor que la translación física. Para R₁ = R₂ = 1, existe una coincidencia exacta entre soluciones analíticas y numéricas.

La sensibilidad de las relaciones de convergencia a los parámetros físicos y numéricos se ha estudiado variando los parámetros dentro de un rango específico. Para el número de Froude F_o, se ha estudiado el siguiente rango: 0.01 ≤ F_o ≤ 0.99. Esto excluye a los regímenes crítico y supercrítico. Para el número de onda σ_{_*}, se ha estudiado el siguiente rango: 0.01 < σ_{_*} < 1,000. Este rango incluye ondas cinemáticas y difusivas (σ_{_*} ≅ 0.01), y las ondas de inercia-presión (σ_{_*} ≅ 1,000). La resolución espacial varía entre π /100 ≤ α ≤ π /10. Este rango incluye tanto una resolución baja (α ≅ π / 10), como una resolución alta (α ≅ π / 100). El número de Courant varía en el rango 0.25 ≤ C ≤ 4.0. El factor de ponderación θ varía en el rango 0 ≤ θ ≤ 1.

El análisis se ha realizado sólo para la onda primaria (8), tomando el signo menos asociado con D y E en las Ecs. 30 y 31. Las limitaciones de espacio impiden un análisis completo de los componentes primarios y secundarios de la propagación de la onda.

Fig. 2 Relación de atenuación R₁ en función de θ, σ_{_*}, F_o y C para: (a) α = π / 10; (b) α = π / 40; (c) α = π / 100.

La Figura 2(a)-2(c) describe la relación de atenuación R₁ como una función de F_o, σ_{_*}, α, C, y θ. El análisis de estas figuras conduce a las siguientes conclusiones:

Para las ondas cinemáticas/difusivas (σ_{_*} ≅ 0.1) y las ondas de inercia-presión (σ_{_*} ≅ 1,000), el número de Froude tiene un efecto insignificante en R₁. Sin embargo, para las ondas dinámicas (σ_{_*} ≅ 10), el efecto de F_o sobre R₁ es bien marcado.
Para un α dado, las relaciones de atenuación para las ondas cinemáticas/difusivas son similares a las de las ondas de inercia-presión. De hecho, la Fig. 2 muestra que para un valor de α dado, los R₁ para valores de σ_{_*} = 0.1 y σ_{_*} = 1,000 son indistinguibles.
Cuanto mayor sea la resolución espacial (menor valor de α) y cuanto menor sea el número de Courant, más se acerca R₁ a 1 para todos los valores de θ.
Para ondas cinemáticas/difusivas y de inercia-presión, la convergencia de la amplitud de onda (R₁ → 1) se obtiene para valores de θ igual o ligeramente superiores a 0.5. Para ondas dinámicas, puede ser necesario un valor de θ mucho mayor de 0.5 con el fin de evitar una cantidad insuficiente de atenuación numérica (R₁ > 1), lo cual está ligado a la amplificación numérica (inestabilidad).

Las siguientes conclusiones se deducen de la Fig. 2:

La simulación es razonablemente precisa para ondas cinemáticas/difusivas y ondas de inercia-presión, siempre que se tenga el cuidado de minimizar la cantidad de atenuación numérica. Se pueden utilizar altos valores de θ (θ acercándose a 1) en conjunción con una alta resolución espacial. Para una resolución espacial baja, es posible que se requieran menores valores de θ (θ reduciéndose hacia 0.5) con el fin de evitar una cantidad excesiva de atenuación numérica.
Para las ondas dinámicas (ondas con resistencia e inercia), la precisión de la simulación depende en gran medida del valor de θ. El valor óptimo de θ es una función de σ_{_*} y α, y, en la práctica, puede ser difícil de determinar.
Los valores de θ < 0.5 siempre causan amplificación numérica; los valores de 0.5 ≤ θ < 1 pueden causar amplificación o atenuación numérica; un valor de θ = 1 siempre causa atenuación numérica (R₁ < 1). La cantidad de atenuación numérica en el rango 0.5 ≤ θ < 1 es una función de F_o, σ_{_*}, α, y C.

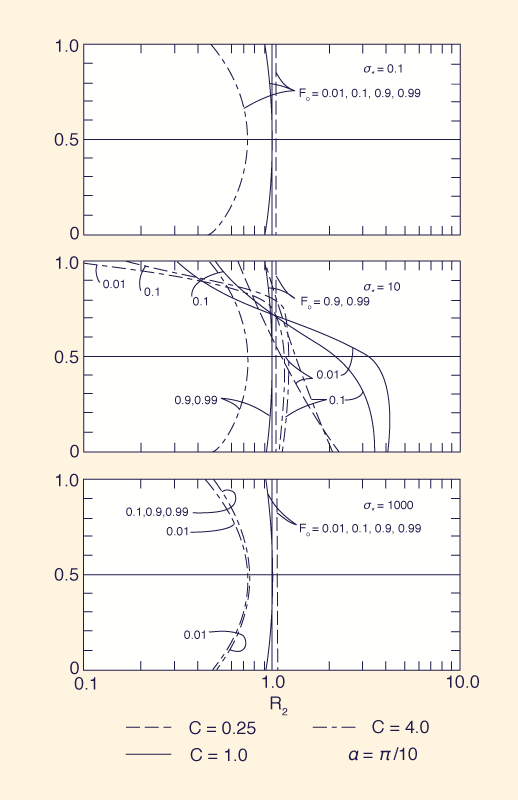
El análisis de la relación de translación R₂ muestra que esta relación se aproxima a la unidad para una amplia gama de parámetros F_o, σ_{_*}, α, y C. Como era de esperar, para números de onda adimensionales de rango medio (σ_{_*} = 10) y baja resolución espacial, las relaciones R₂ se alejan de la unidad. Como ilustración de esta tendencia, la Fig.3 muestra los valores de R₂ para diferentes F_o, σ_{_*}, C, y θ, y α = π / 10.

Fig. 3 Relación de translación R₂ en función de θ, σ_{_*}, F_o y C para: α = π / 10.

7. RESUMEN Y CONCLUSIONES

Se presenta un análisis teórico de la convergencia del modelo numérico implícito de cuatro puntos de ondas de aguas poco profundas. Se derivan la celeridad de propagación y el factor de atenuación de la solución numérica, y la convergencia se evalúa estableciendo las relaciones de atenuación y translación dada por las soluciones numéricas y analíticas. Se muestra que la convergencia es una función de la interacción compleja de cinco parámetros: (1) El número de Froude del flujo de equilibrio F_o; (2) el número de onda adimensional σ_{_*} = (2π/L) (d_o/S_o); (3) la resolución espacial α = π/(L/Δx); (4) el número de Courant C = c / (Δx/Δt); y (5) el factor de ponderación θ del esquema implícito.

El análisis de convergencia se realiza para números de Froude en régimen subcrítico. Además, debido a las limitaciones de espacio, solo se analiza la convergencia de la onda primaria.

Se presentan las siguientes conclusiones:

La simulación es razonablemente apropiada para pequeñas ondas σ_{_*} (cinemáticas/difusivas) y para grandes ondas σ_{_*} (inercia-presión), siempre que se tenga el cuidado suficiente de minimizar la cantidad de atenuación numérica.
Para ondas intermedias σ_{_*} (ondas dinámicas, en las que predominan tanto la fricción como la inercia), la precisión de la simulación depende en gran medida del valor correcto del factor de ponderación θ. En la práctica, puede ser difícil determinar un valor óptimo de θ para asegurar tanto la estabilidad como la convergencia.
Los valores de θ < 0.5 siempre causan amplificación numérica; los valores de 0.5 ≤ θ < 1 puede causar amplificación o atenuación numérica; y θ = 1 siempre causa atenuación numérica.

8. LIMITACIONES Y APLICACIONES

Los resultados de este artículo se han obtenido utilizando una versión linealizada de las ecuaciones de Saint Venant. Por lo tanto, se hace énfasis en la naturaleza cualitativa de los resultados. En la actualidad, la bondad de un modelo no lineal sólo puede evaluarse mediante experimentos numéricos cuidadosamente diseñados. El análisis lineal presentado en este artículo provée un marco apropiado para el diseño de estos experimentos.

AGRADECIMIENTOS

El tema de investigación de este artículo fue apoyado en parte por la Estación Experimental de la Universidad Estatal de Colorado. Horst Indlekofer recibió una beca de la OTAN para hacer posible su visita a la Universidad Estatal de Colorado.

APÉNDICE Ι. ECUACIONES PARA LA CELERIDAD DE PROPAGACIÓN c_{_*} Y DECREMENTO LOGARITMICO δ DE PERTURBACIONES SINUSOIDALES EN EL FLUJO EN CANALES (8)

Estas ecuaciones son: c_{_*} = 1 ± D; δ = -2π (B ∓ E)/(|1 ± D |), en la cual A = (1/F_o^²) - B^²; B = 1/(σ_{_*} F_o^²); C = (A^² + B^²)^{^1/2}; D = [(C + A)/2]^{^1/2}; E = [(C - A)/2]^{^1/2}; F_o = u_o / (gd_o)^{^1/2}; y σ_{_*} = (2π / L)(d_o / S_o).

APÉNDICE ΙΙ. BIBLIOGRAFÍA

Chaudhry, Y. M., y D. N. Contractor. 1973. "Application of the Implicit Method to Surges in Open Channels," Water Resources Research, Vol. 9, No. 6, Dec., pp. 1605-1612.

Cunge, J. A., y M. Wegner. 1694. "Numerical Integration of the Saint Venant Equations by an Implicit Finite Difference Scheme," La Houille Blanche, Grenoble, France, Vol. 19, No. 1, Jan., pp. 33-39.

Fread, D. L. 1974. "Numerical Properties of Implicit Four-Point Finite Dfference Equations of Unsteady Flow," NOAA Technical Memorandum NWS HYDRO-18, National Oceanic and Atmospheric Administration, Mar.

Liggett, J. A. 1975. "Basic Equations of Unsteady Flow," Unsteady Flow in Open Channels, K. Mahmood and V. Yevjevich, eds., VoL. I, Water Resources Publications, Fort Collins, Colo.

Liggett, J. A., y J. A. Cunge. 1975. "Numerical Methods of Solution of the Unsteady Flow Equations," Unsteady Flow in Open Channels, K. Mahmood and V. Yevjevich, eds., Vol. I, Water Resources Publications, Fort Collins, Colo.

Lighthill, M. J., y G. B. Whitham. 1955. "On Kinematic Waves I, Flood Movements in Long Rivers," Proceedings, Royal Society of London, Vol. A 229, May, pp. 281-316.

O'Brien, G. G., M. A. Hyman, y S. Kaplan. 1950. "A Study of the Numerical Solution of Partial Differential Equations," Journal of Mathematics and Physics, Vol. 29, No. 4, pp. 223-251.

Ponce, V. M., y D. B. Simons. 1977. "Shallow Wave Propagation in Open Channel Flow," Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, Proc. Paper 13392, Dec., pp. 1461-1476.

Price, R. K. 1974. "Comparison of Four Numerical Methods of Flood Routing," Journal of the Hydraulics Division, ASCE. Vol. 100, No. HY7, Proc. Paper 10659, July, 1974, pp. 879-899.

Quinn, F. H., y E. B. Wylie. 1972. "Transient Analysis of the Detroit River by the Implicit Method," Water Resources Research, Vol. 8, No. 6, Dec., pp. 1461-1469.

Roache, P. J. 1972. Computational Fluid Dynamics, Hermosa Publishers, Albuquerque. N. M.

APÉNDICE ΙΙΙ. SIMBOLOGÍA

Los siguiente símbolos son usados en este artículo:

A, B, C, D, E = parámetros, Eqs. 24-28;

a = amplitud de onda;

C = número de Courant;

c = celereridad de onda;

d = profundidad de flujo;

F_o = número de Froude;

ƒ = función;

g = aceleración de la gravedad;

i = √-1;

j = índice de discretización espacial;

L = longitud de onda;

M, M_o, M₁, M₂ = parámetros;

N, N_o, N₁, N₂ = parámetros;

n = índice de discretización temporal;

P, Q = parámetros;

R₁ = relación de convergencia de atenuación;

R₂ = relación de convergencia de translación;

S_ƒ = pendiente de fricción;

S_o = pendiente de fondo;

T = período de onda;

t = variable tiempo;

t_o = tiempo inicial;

u = velocidad media;

x = variable de espacio;

α = parámetro de resolución espacial;

β_{_*} = factor de propagación complejo;

β_{_*}_{_i} = parte imaginaria de β_{_*};

β_{_*}_{_R} = parte real de β_{_*};

Δx = intervalo de espacio;

Δt = intervalo de tiempo;

δ = decremento logarítmico;

θ = factor de ponderación; y

σ_{_*} = número de onda adimensional.

Subíndices

o = flujo de equilibrio; y

n = numérico.

Superíndice

' = componente perturbada; y

* = variable adimensional.

220709

Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader.