1.  INTRODUCCIÓN

El método de Muskingum y sus variantes están bien establecidos en la literatura sobre el enrutamiento de inundaciones. Tradicionalmente, sus parámetros K y X se han determinado mediante calibración utilizando hidrogramas medidos, de entrada y salida. Una versión mejorada se debe a Cunge (4), quien demostró que los parámetros K y X estan relacionados con el problema físico, eliminando así la necesidad de calibración, mejorando así la capacidad predictiva del método.

Con la ayuda de los resultados de Cunge, los cálculos pueden realizarse fijando constantes los parámetros de enrutamiento (5), o utilizando parámetros variables (6,7). El método de parámetros constantes tiene la ventaja de simplicidad, aunque ésto se logra a costa de alguna pérdida de detalle. Por otro lado, el modo de parámetros variables deja de lado la simplicidad a cambio de un mayor detalle en la definición del hidrograma. Dadas estas diferencias, es de esperar que ambos enfoques continuen utilizándose en el futuro. Cuando está en juego la simplicidad, se aplica el método de parámetros constantes; cuando es necesario una mayor precisión, el método de parámetros variables es recomendable.

Los cálculos para el método de parámetros constantes pueden ser de dos formas. La forma convencional es especificar intervalos de tiempo y espacio Δx y Δt; los parámetros K y X se calculan a partir de éstos. Una forma alternativa es especificar K y X, y calcular Δx y Δt en base a éstos. Como se muestra aquí, la elección apropiada de los parámetros conduce a una simplificación considerable en la ecuación de enrutamiento. Esto permite obtener una solución razonable al problema del enrutamiento de inundaciones, con un mínimo de esfuerzo.

2.  MÉTODO MUSKINGUM

En el método Muskingum, el caudal de flujo Q_j+1ⁿ⁺¹ se expresa de la siguiente manera (Fig.1):

Qj+1n+1 = C1 Qj n + C2 Q j n + 1 + C3 Qj + 1 n

(1)

en la cual C₁, C₂, y C₃ son coeficientes definidos como sigue:

Δt                 ______  +  2X                    K C1 = _______________________               Δt            ______  +  2 ( 1 - X )               K

(2)

Δt                 ______  -  2X                    K C2 = _______________________                Δt             ______  +  2 ( 1 - X )                K

(3)

Δt              2 ( 1 - X ) - ______                                   K C3 = _______________________               Δt             ______  +  2 ( 1 - X )                K

(4)

3.  ECUACIÓN DE ENRUTAMIENTO SIMPLIFICADA DE MUSKINGUM

En las Ecs. 2-4, si Δt /K y X son especificadas como sigue:

Δt               _____  =  1       K

(5)

y

X  =  0

(6)

resulta que:

1 C1 = C2 = C3 = ______                             3

(7)

lo cual conduce a la forma simplificada de la ecuación de enrutamiento de Muskingum de la siguiente manera:

Q j n + Q j n+1 + Q j+1 n             Qj+1n+1  =  ________________________                                    3

(8)

El cumplimiento de las Ecs. 5 y 6 implica que Δx y Δt está fijado. En efecto, K se define como el tiempo que tarda un caudal de inundación en recorrer la distancia Δx con la celeridad c:

Fig. 1  Discretización espacio-temporal en el método Muskingum.

Δt            K  =  ______             c

(9)

Por lo tanto, de las Ecs. 5 y 9:

c Δt            C  =  ________  = 1              Δx

(10)

en la cual C = número de Courant. La Ecuación 10 especifica que la celeridad de la onda de inundación c debe ser igual a la "celeridad de la malla" Δx /Δt.

Cunge (4) ha demostrado que el parámetro X puede estar relacionado con el problema físico de la siguiente manera:

1                   q X  =  ___  ( 1 -  __________ )          2              So c Δx

(11)

en la cual q = caudal por unidad de ancho; y S_o = pendiente de fondo. Las Ecuaciones 6 y 11 conducen a:

q D  =  __________ = 1           So c Δx

(12)

en la cual D = número de Reynolds de la malla. La Ecuación 12 especifica que la difusividad del canal q /(2S_o) debe ser igual a la "difusividad de la malla" (cΔx)/2. Las Ecuaciones 10 y 12 permiten el cálculo de Δx y Δt en función de las variables de flujo. En este sentido, debe tenerse en cuenta que el intervalo de espacio calculado a partir de la Ec. 12 es la misma que la "longitud característica" en la que se basa el método de Kalinin-Milyukov (6). Si bien se reconoce esta similitud, el método propuesto en este documento tiene su propio mérito, ya que conduce a una ecuación de enrutamiento (Ec. 8) mucho más simple que la del método de Kalinin-Milyukov.

---

De las Ecs. 10 y 12, los intervalos de tiempo y espacio están dados por las siguientes fórmulas:

q            Δx  =  _______             So c

(13)

y

Δx           q Δt  =  _____ = ________               c         So c 2

(14)

Para canales naturales, la fricción del canal y la forma de la sección transversal se establecen implícitamente en la relación caudal-área en estado permanente.

Q = α A β

(15)

en la cual Q = caudal, A = área de la sección transversal; y α y β = coeficiente y exponente, respectivamente. La celeridad de la onda de inundación es la celeridad de la onda cinemática, definida de la siguiente manera:

dQ                              βQ          β B q c  =  _______ = α β A  β-1  =  _____  =  ________            dA                                A              A

(16)

en la cual B = ancho superior. De las Ecs. 13 y 16 se obtiene:

A            Δx  =  __________               β B So

(17)

y

Δx               A 2 - β Δt  =  ______  =  _____________              c             α β 2 B So

(18)

Al igual que con todos los modelos de parámetros agrupados (5), se requiere cierto juicio en la elección de las variables hidráulicas de referencia (es decir, q, A y B en las Ecs. 16-18) en el cual basar los cálculos de Δx y Δt. El uso de cantidades medias suele ser suficiente desde el punto de vista práctico.

5.  PRUEBA DEL MODELO

La prueba de un modelo matemático generalmente depende de si el modelo puede reproducir datos medidos en el campo. Sin embargo, si hay discrepancias es muy difícil, y a veces imposible, determinar si se deben a errores en la solución numérica, en la estimación de los parámetros, o en los datos medidos. Un procedimiento actualmente cuestionado consiste en agrupar todos estos errores, y ajustar los parámetros del modelo para que estén de acuerdo con los datos medidos, en lo que se ha dado en llamar "calibración".

Un mejor enfoque consiste en aislar las fuentes de error para estudiar sus efectos por separado. Esto se hace mediante la realización de una prueba hipotética y una prueba de datos reales. La prueba hipotética está diseñada para aislar los efectos de la precisión numérica en los resultados del modelo. Por otro lado, la prueba de datos reales está diseñada para proporcionar información sobre la precisión de la estimación de los parámetros. Los errores en los datos medidos sólo pueden evaluarse desde un punto de vista cualitativo.

Prueba hipotética.  Para probar el método propuesto en este artículo, se estableció una prueba hipotética utilizando el método del ejemplo clásico de Thomas (10). Se realizaron las dos siguientes simulaciones: (1) simulación de prueba usando el método simplificado; y (2) simulación de control usando el método convencional. En la simulación de prueba, se tomó X = 0, y K = Δt. En consecuencia, los intervalos de espacio y de tiempo fueron los siguientes: Δx = 13.5 millas (21.7 km), y Δt = 2.16 hr.

En la simulación de control, los intervalos de espacio y de tiempo se especificaron en Δx = 25 millas (40 km), y Δt = 6 hr. Esto resultó en X = 0.228 y K = Δt /1.5. En ambas pruebas se utilizaron las siguientes variables hidráulicas: (1) caudal base = 50 pies³/s (1.4 m³/s); (2) caudal pico = 200 pies³/s (5.7 m³/s); (3) caudal de referencia = 125 pies³/s (3.54 m³/s); (4) longitud del canal = 500 millas (800 km), y (5) pendiente de fondo = 1 pie/milla (0.19 m/km).

Los resultados calculados para el flujo de salida máximo = 177 pies³/s (5.1 m³/s), el tiempo de traslación = 128 horas, y la forma del hidrograma fueron esencialmente los mismos para ambas simulaciones. Por lo tanto, la demostrada independencia de la malla debe tomarse como una medida de la solidez del método simplificado.

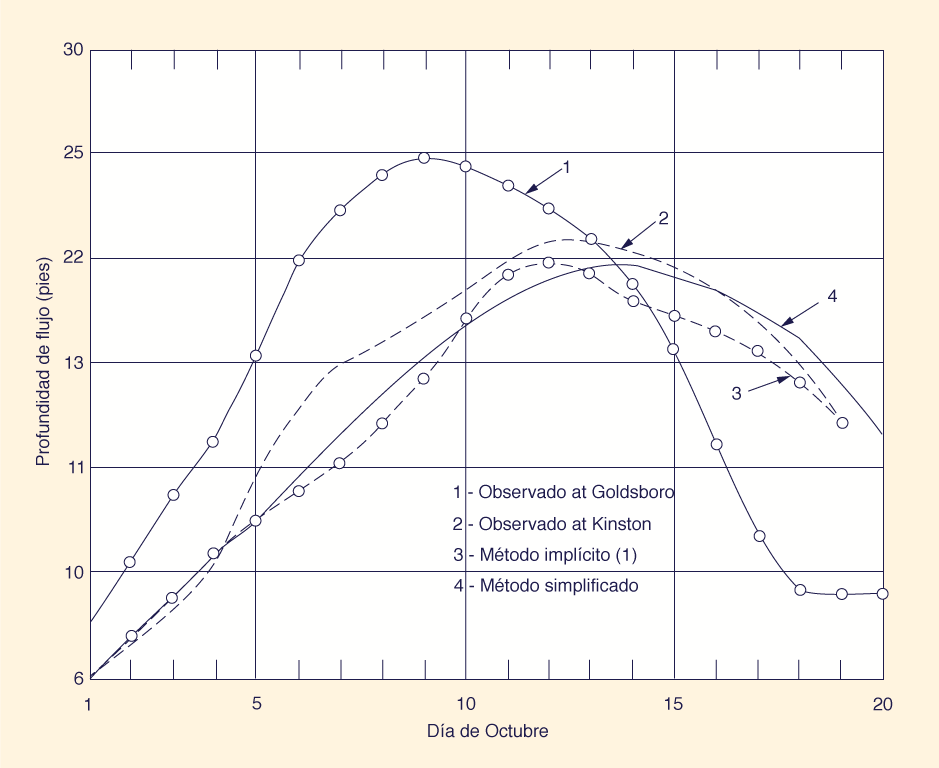
Prueba de datos reales.   Se estableció una prueba de datos reales utilizando datos de inundaciones medidos por el Servicio Geológico de los Estados Unidos en el tramo de 45 millas (72 km) del río Neuse, entre Goldsboro, N.C. y Kinston, N.C., para probar aún más el método propuesto. Los detalles de los datos se dan en Amein y Fang (1) y Chen (3).

El área de la sección transversal de referencia y el ancho superior se eligieron para corresponder a la profundidad hidráulica promedio en el tramo: A = 17,900 pies² (1,660 m²); y B = 2,900 pies (890 m). Las constantes de la curva de gasto son las siguientes: α = 12, y β = 0.74; y la pendiente de fondo es S_o = 0.000133. De las Ecs. 17 y 18, los intervalos de tiempo y espacio son Δx = 11.9 millas (19 km), y Δt = 25 hr. Estos valores se ajustaron aún más a Δx = 11.25 millas (18 km) y Δt = 24 hr, proporcionando así un número par de puntos de la malla (cuatro tramos computacionales y 19 intervalos de tiempo). Para tener en cuenta la entrada lateral, la descarga calculada por la Ec. 8 se corrigió agregando Q_L = 2 q_L Δx /3 = 396 pies³/s (11.2 m³/s) en cada celda computacional (Apéndice I).

Fig. 2  Hidrogramas de inundación de octubre de 1964 medidos y calculados
en Goldsboro (entrada) y Kinston (salida), Carolina del Norte (1 pie = 0.305 m).

Se hacen las siguientes observaciones (Fig. 2):

1. Ninguno de los métodos puede reproducir exactamente el hidrograma medido en Kinston. La razón de esto radica en la incertidumbre con respecto a la cantidad de flujo lateral, el cual probablemente depende del espacio y el tiempo. Amein y Fang (1) han documentado la sensibilidad de los resultados calculados al flujo lateral y han utilizado una constante q_L (flujo lateral) en su modelo.

2. La Tabla 1 muestra una comparación de los resultados para la profundidad del flujo máximo y el intervalo de tiempo de los datos medidos, el método implícito y el método simplificado. En vista de las incertidumbres involucradas en la estimación de la cantidad de flujo lateral, los resultados del método simplificado están dentro de un rango razonable.

3. El método simplificado pertenece a la familia de modelos de ondas de difusión. La aplicabilidad de estos modelos se ha tratado en detalle en las referencias 8 y 9.

---

Se desarrolla una ecuación simplificada de enrutamiento con el método de Muskingum. El método se basa en la especificación de los intervalos de tiempo y espacio Δx y Δt de tal manera que X = 0 y K = Δt. En este caso, la ecuación de enrutamiento se reduce al cálculo de un simple promedio. La prueba del método muestra que se pueden obtener resultados razonablemente precisos con un mínimo de esfuerzo.

APÉNDICE I.  DERIVACIÓN DEL TÉRMINO DEL FLUJO LATERAL

La ecuación de enrutamiento de Muskingum con flujo lateral es la siguiente:

Qj+1 n+1 = C1 Qj n + C2 Qj n+1 + C3 Q j+1 n + QL

(19)

en la cual

2 c qL Δt QL = _______________________                 Δt             _______ + 2 ( 1 - X )                  K

(20)

Desde que c = Δx / K, y para la condición K = Δt, y X = 0, la Ec. 20 se reduce a lo siguiente:

2 qL Δx            QL  =  ____________                    3

(21)

APÉNDICE II.  BIBLIOGRAFÍA

1. Amein. M., y C. S. Fang. 1970. "Implicit flood routing in natural channels," Journal of the Hydraulics Division, ASCE, VOL 96, No. HY12, Proc. Paper 7773, Dec., pp. 2481-2500.

2. Basco, D. 1975. "On numerical accuracy in computational hydraulics," Proceedings, 25th Hydraulics Division Specialty Conference, ASCE, College Station, TX, pp. 179-186.

3. Chen, Y. H. 1973. "Mathematical modeling of water and sediment routing in natural channels," Thesis presented to Colorado State University at Fort Collins, CO, in partial fulfillment of the requirement for the degree of Doctor of Philosophy.

4. Cunge, J. A. 1969. "On the subject of a flood propagation computation method (Muskingum method)," Journal of Hydraulic Research, VoL 7, No. 2, pp. 205-230.

5. Dooge, J. C. I. 1973. "Linear theory of hydrologic syslems," Technical Bulletin No. 1468, USDA Agricultural Research Service, Oct.

6. Miller, W. A., y J. A. Cunge. 1975. "Simplified equations of unsteady flow," Unsteady Flow In Open Channels, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Fort Collins, Colo., pp. 183-257.

7. Ponce, V. M., y V. Yevjevich. 1978. "The Muskingum-Cunge method with variable parameters," Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY12, Proc. Paper 14199, Dec.

8. Ponce, V. M., R. M. Li, y D. B. Simons. 1978. "Applicability of kinematic and diffusion models," Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY3, Proc. Paper 13635, Mar., pp. 351-160.

9. Ponce, V. M., V. Yevjevich, y D. B. Simons. 1978. "The numerical dispersion of the Muskingum method," Proceedings, 26th Hydraulics Division Specialty Conference, ASCE, College Park, MD, Aug.

10. Thomas, H. A. 1934. "The hydraulics of flood movement in rivers," Carnegie Institute of Technology, Pittsburgh, PA.