1. INTRODUCCIÓN El cálculo del transporte de sedimentos está lleno de complicaciones, incluyendo el rol de la fricción (grano y forma), acorazamiento, flujo no permanente y otros. A pesar de estas dificultades, en la práctica es posible desarrollar una curva de gasto de sedimentos en base a una fórmula de transporte de sedimentos y/o mediciones de campo. La curva de gasto de sedimentos es un gráfico que relaciona el caudal sólido (toneladas/día) y el caudal líquido (pies cúbicos por segundo), por lo general en una escala logarítmica. Para los caudales altos, la curva de gasto de sedimentos tiende asintóticamente a una concentración máxima (American Society of Civil Engineers 1975, p. 476), es decir, asintótica a una línea de 45°. Ponce (1988) examinó esta característica de la curva de sedimentos y se refirió al valor máximo como la concentración última de sedimento. La naturaleza de la curva de gasto de sedimentos, en la cual la concentración (a) aumenta con el caudal, y (b) es asintótica a un valor máximo para caudales suficientemente altos, sugiere que existe un mecanismo que reduce la concentración de sedimentos para caudales bajos. Aquí sugerimos que este mecanismo es la fricción de forma. El objetivo de este estudio es demostrar, utilizando datos de campo de alta calidad, que la fricción de forma es la causante principal de la curvatura y la forma de la curva de sedimentos para caudales bajos. Este estudio confirma que para caudales altos, la curva de gasto de sedimentos tiene la tendencia a acercarse asintóticamente a una concentración máxima (American Society of Civil Engineers 1975). Para caudales bajos, la fricción de forma reduce la concentración de sedimentos por debajo de lo que se podría lograr si la fricción de forma fuera insignificante. El efecto neto de la fricción de forma es producir una reducción de la concentración de sedimentos muy por debajo del valor último (Colby 1964; Ponce 1988). Esto aumenta considerablemente la complejidad del cálculo de transporte de sedimentos para caudales bajos. Einstein (1950) fue aparentemente el primero en separar la fricción total del canal aluvial en sus componentes: (a) fricción de grano, y (b) fricción de forma. Einstein argumentó que la parte de la energía que se gasta en la fricción de forma no contribuye al movimiento de carga sólida; por lo tanto, podría ser omitida en el cálculo de la carga de sedimentos (op. cit., página 9). Esto encaja admirablemente con nuestra conclusión de que el efecto de la fricción de forma es reducir la descarga de sedimentos debajo de la que podría obtenerse únicamente con la fricción del grano.
2. DATOS DE CAMPO En este estudio, hemos utilizado los datos recopilados por Williams (1995), quien presentó una base de datos digitales incluyendo los de Ackers y White (1973), Brownlie (1981 a, b), Engelund y Hansen (1967) y Yang (1973) en el desarrollo de fórmulas de transporte de sedimentos. Específicamente, los datos de Brownlie incluyen aproximadamente 7,000 datos de campo y de laboratorio. Williams (1995) filtró los datos para incluir sólo los datos con las siguientes características:
Dentro de cada conjunto de datos, cada unidad de datos consistió de lo siguiente:
Los datos del Río Niobrara también incluyen los tipos de forma de fondo.
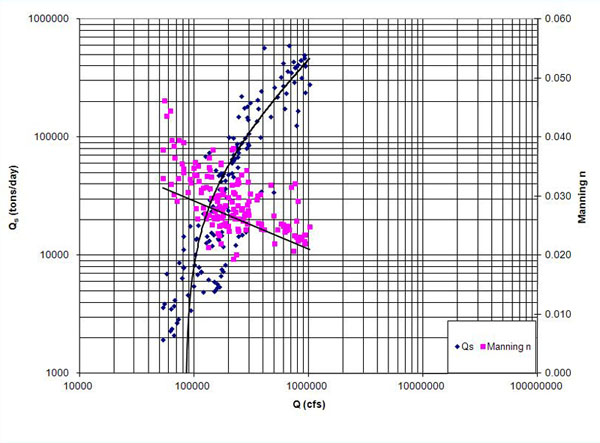
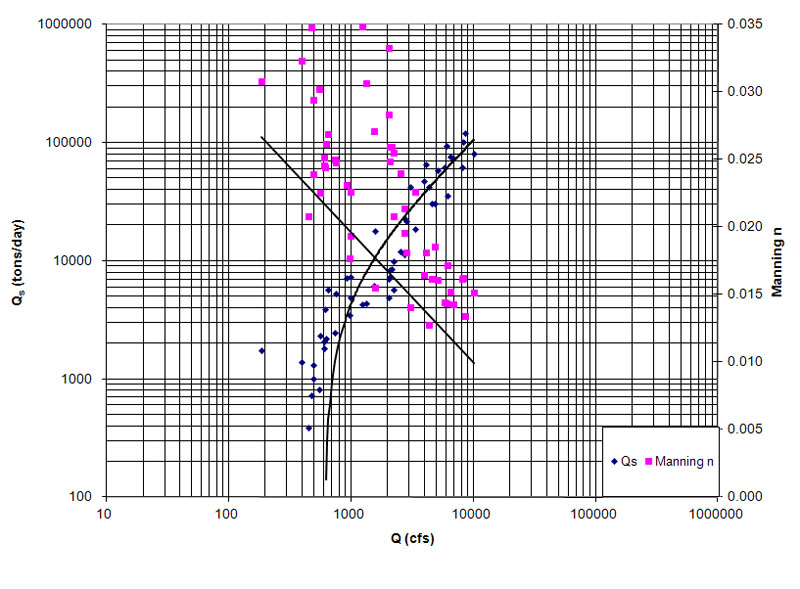
3. METODOLOGÍA Y RESULTADOS Las curvas de gasto de sedimentos, incluyendo el mejor ajuste gráfico, se muestran en las Figuras 1 (a) a 1 (f). Además, por cada unidad de datos, el caudal, el ancho de canal, la profundidad hidráulica, y la pendiente del lecho se utilizaron para calcular el número de Manning (Chow 1959). Para simplificar, se ha supuesto un canal rectangular. Por cada medición, el número de Manning se muestra en un eje vertical paralelo, de modo que la tendencia en la curva de sedimentos pueda ser comparada con la tendencia en el número de Manning. En todos los casos, se ve claramente que el número de Manning disminuye a medida que el caudal líquido y el caudal sólido aumentan.
Figura 1 (a) Curva de gasto de sedimentos para el Río Atchafalaya.
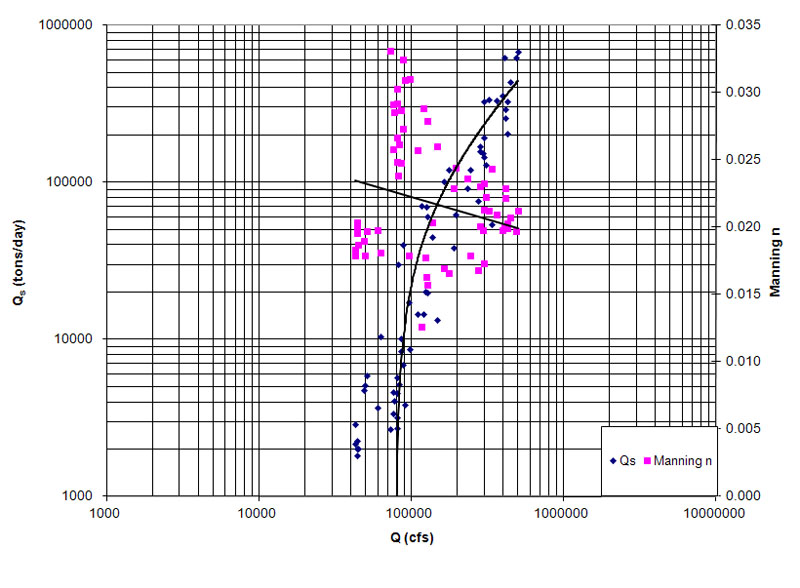
Figura 1 (b) Curva de gasto de sedimentos para el Río Niobrara.
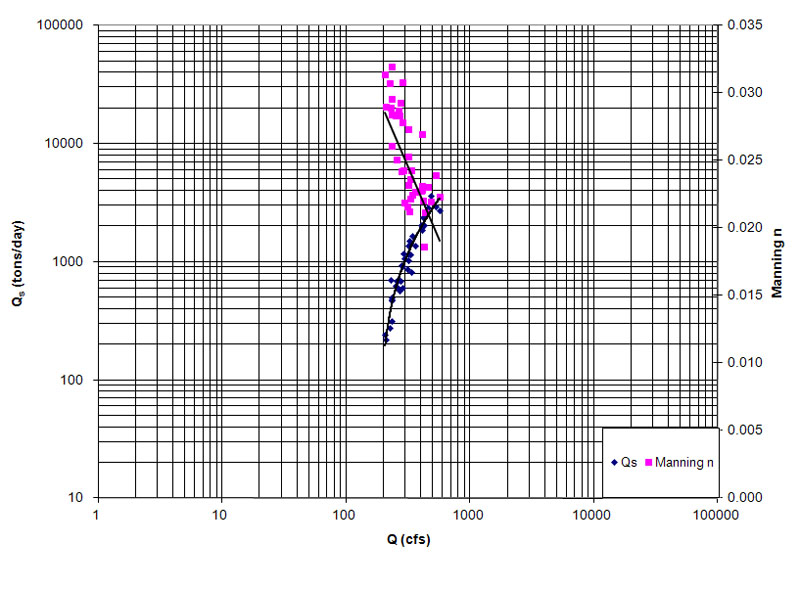
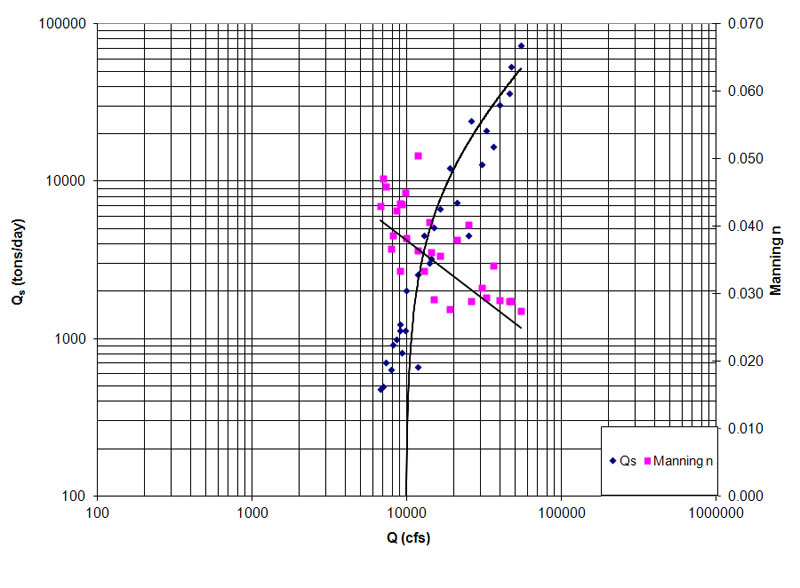
Figura 1 (c) Curva de gasto de sedimentos para el Río Middle Loup.
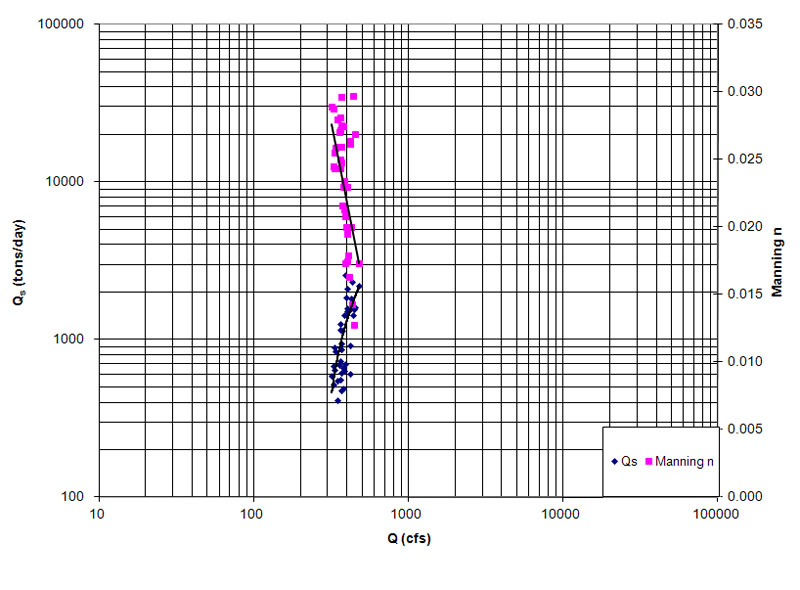
Figura 1 (d) Curva de gasto de sedimentos para el Río Grande.
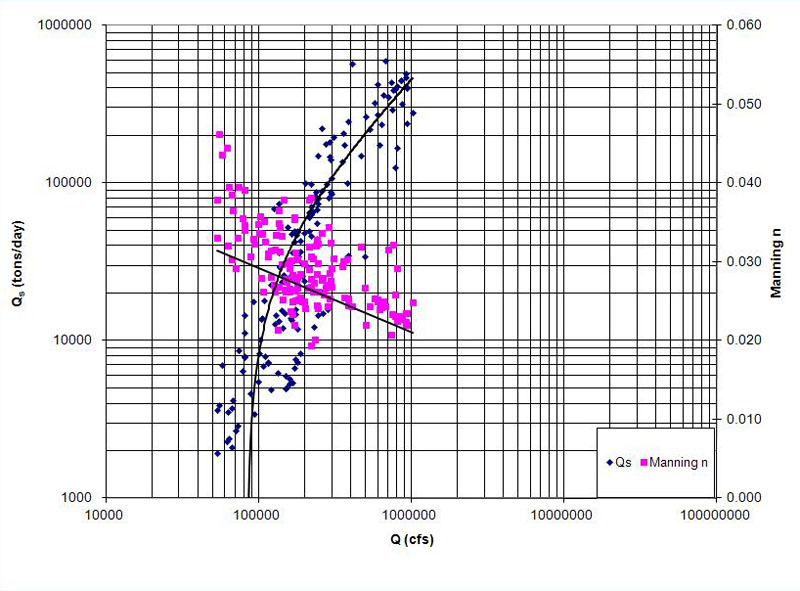
Figura 1 (e) Curva de gasto de sedimentos para el Río Mississippi.
Figura 1 (f) Curva de gasto de sedimentos para el Río Red.
4. CONCLUSIONES Se ha utilizando un conjunto de datos de campo de alta calidad, para demostrar que la fricción de forma es la causante de la curvatura y la forma típica de las curvas de gasto de sedimentos. Se ha confirmado que para caudales altos, las curvas de gasto de sedimentos tienden asintóticamente a una concentración máxima. Por el contrario, para caudales bajos, la fricción de forma reduce la concentración de sedimentos muy por debajo de lo que se podría lograr si la fricción de forma fuera despreciable. Se han mostrado seis curvas de gasto de sedimentos, efectuadas con mediciones de alta calidad. Además, por cada unidad de datos, el caudal, el ancho de canal, la profundidad hidráulica, y la pendiente del lecho se utilizaron para calcular el número de Manning. Los datos se representaron gráficamente de tal manera que la tendencia en al gasto de sedimentos pueda ser fácilmente comparada con la tendencia del número de Manning. En todos los casos, el número de Manning disminuye a medida que el caudal líquido y el caudal sólido aumentan. Se concluye que para caudales bajos, la fricción de forma es significativa en el transporte de sedimentos, reduciendo eficazmente la concentración de sedimentos muy por debajo del valor último. Para caudales altos la fricción de forma disminuye, la fricción total tiende a un valor constante, y la concentración de sedimentos se acerca asintóticamente al valor último. Estos resultados iluminan nuestro entendimiento de la curva de gastos en particular y el transporte de sedimentos en general.
BIBLIOGRAFÍA
Ackers, P., and W. R. White (1973). "Sediment transport: New approach and analysis," Journal of Hydraulic Engineering, ASCE, 99(11), 2041-2060.
American Society of Civil Engineers. (1975). Sedimentation Engineering. ASCE Manuals and Reports on Engineering Practice - No. 54, New York, NY.
Brownlie, W. L. (1981a). "Prediction of flow depth and sediment discharge in open channels," Report KH-R-43A, W.M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, Pasadena, California.
Brownlie, W. L. (1981b). "Compilation of alluvial channel data: Laboratory and field," Report KH-R-43B, W.M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, Pasadena, California.
Chow, V. T. (1959). Open-channel Hydraulics. McGraw-Hill, New York.
Colby, B. R. and C. H. Hembree (1955). "Computations of total sediment discharge, Niobrara river near Cody, Nebraska." U.S. Geological Survey Water Supply Paper No. 1351, Washington, D.C.
Colby, B. R. (1964). "Discharge of sands and mean-velocity relations in sand-bed streams," U.S. Geological Survey Professional Paper 462-A, Washington, D.C.
Einstein, H. A. (1950). "The bed-load function for sediment transportation in open channel flows," Technical Bulletin No. 1026, U. S. Dept. of Agriculture, Soil Conservation Service, Washington, D.C., September.
Engelund, F., and E. Hansen. (1967). "A monograph on sediment transport in alluvial streams," Teknisk Vorlag, Copenhagen, Denmark.
Hubbell, D. W. and D. Q. Matejka (1959). "Investigations of sediment transportation, Middle Loup river at Dunning, Nebraska." U. S. Geological Survey Water Supply Paper No. 1416, Washington, D.C.
Nordin, C. F., Jr. and J. P. Beverage (1965). "Sediment transport in the Rio Grande, New Mexico." U. S. Geological Survey Professional Paper No. 462-F, Washington,
D.C.
Ponce, V. M. (1988). "Ultimate sediment concentration." Proceedings, 1988 National Conference of Hydraulic Engineering, American Society of Civil Engineers Hydraulics Division,
New York, 311-315.
Toffaleti, F. B. (1968). "A Procedure for computation of the total river sand discharge and detailed distribution, bed to surface." Technical Report No. 5, Committee on Channel Stabilization, Corps of Engineers, United States Army, Vicksburg, Mississippi.
Williams, D. T. (1995). "Selection and predictability of sand transport relations based upon a numerical index," Ph.D. dissertation, Department of Civil Engineering, Colorado State University, Fort Collins, Colorado.
Yang, C. T. (1973). "Incipient motion and sediment transport." Journal of the Hydraulics Division, ASCE, 99(10), 1679-1704.
1
Profesor de Ingeniería Civil y Ambiental,
Universidad Estatal de San Diego, California.
|
| 150227 07:00 |