1. INTRODUCCIÓN Las propiedades de estabilidad y convergencia de los esquemas numéricos explícitos de la ecuación de convección pura se conocen desde hace algún tiempo. Aquí se presenta un tratamiento teórico unificado. Los análisis de von Neumann (4) y Hirt (2) se utilizan para mostrar cómo la estabilidad incondicional y la precisión de segundo orden son posibles dentro del marco de un esquema explícito (6).
2. ECUACIÓN DE CONVECCIÓN PURA La ecuación de convección pura tiene la siguiente forma:
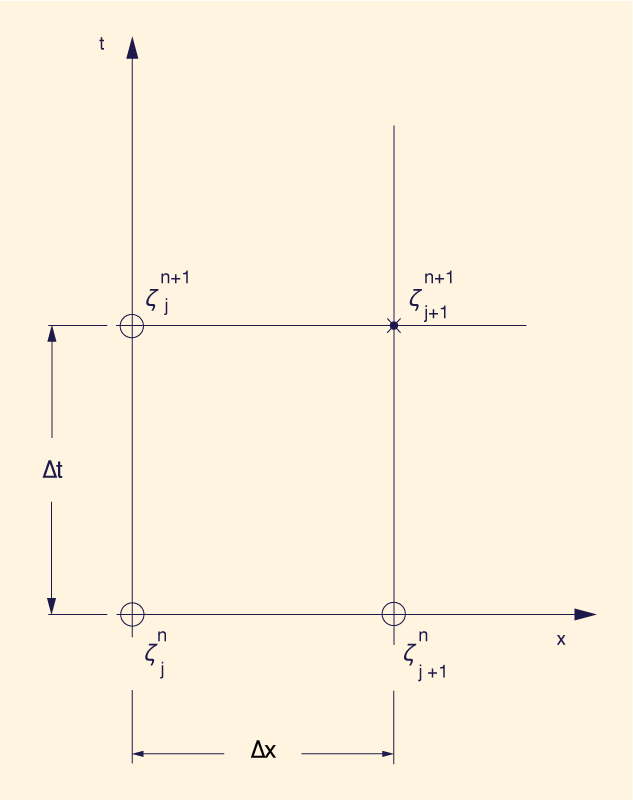
en la cual ζ = cantidad física a ser convectada con la velocidad u. Un esquema general explícito de diferencias finitas de esta ecuación es el siguiente (Fig.1):
en la cual X y Y = factores de ponderación de las derivadas temporal y espacial, respectivamente; Δt y
En la Ecuación 2, resolviendo explícitamente el valor desconocido ζ j+1 n+1 :
en la cual:
y
es el número de Courant correspondiente a una ubicación particular de la malla. 3. COEFICIENTE DE DIFUSIÓN NUMÉRICA La Ecuación 1 es una ecuación no viscosa; por lo tanto, la viscosidad (o difusividad, según el caso) está ausente. Sin embargo, una solución numérica de la ecuación, a menudo muestra un comportamiento viscoso (difusivo). Esto debe atribuirse correctamente a la viscosidad artificial del propio esquema. El término "dispersión numérica" se utiliza a veces, aparentemente para indicar el hecho de que tanto los errores de amplitud como los de fase se agregan para producir un efecto de tipo dispersivo en la solución numérica. Se puede obtener una medida de la cantidad de dispersión numérica a partir del error de aproximación del esquema de diferencias finitas. Esto se puede obtener expandiendo la función de malla ζ(jΔx, nΔt) en una serie de Taylor sobre el punto jΔx, nΔt, lo cual conduce a lo siguiente (1,2):
en la cual R = error de aproximación. A partir de la Ec. 8, para X = Y = 1/2, el esquema es de precisión de segundo orden, es decir, R = ο(Δx2). Además, para C = 1, la precisión es de tercer orden. De hecho, para estas condiciones se obtiene la solución exacta (1). El coeficiente del término ∂2ζ /∂x2 en la Ec. 8 se conoce como el coeficiente de difusión numérica, μn, definido como sigue:
Los valores positivos de μn hacen que en la amplitud de la onda haya difusión numérica; los valores negativos hacen que la amplitud de la onda se amplifique numéricamente. Mientras que en el primero la consistencia se ve afectada, en el segundo la estabilidad se ve afectada. Tanto la estabilidad como la consistencia mejoran a medida que μn tiende a cero. La Tabla 1 resume las propiedades de estabilidad y convergencia (consistencia en el límite) de tres esquemas usuales de primer orden.
4. ANÁLISIS LINEAL DE VON NEUMANN Se puede obtener una visión amplia de las propiedades numéricas de los diversos esquemas explícitos de cuatro puntos para el cálculo de convección pura mediante un análisis lineal de estabilidad y convergencia siguiendo el enfoque de von Neumann (3,4). De acuerdo con este método, se busca una solución de la Ec. 2 en la siguiente forma sinusoidal:
en la cual ζο = función de amplitud; σ = número de onda de la solución sinusoidal; y β = factor complejo de propagación, de tal manera que
Sustituyendo exp(i σ Δx) = p + i q, en la cual p = cos (σΔx) y q = sin (σΔx) en la Ec. 11 conduce a:
en la cual:
Operando en la Ec. 12 se obtiene:
en la cual:
y
Separando la Ec. 15 en sus componentes reales e imaginarios:
Dado que la solución analítica de la Ec. 1 no exhibe atenuación, se deduce que la Ec. 20 es una medida de la atenuación (o amplificación) numérica de la solución numérica, después de un incremento de tiempo Δt. Una relación de convergencia con respecto a la amplitud de onda se define de la siguiente manera:
De la Ecuación 19, la velocidad de fase de la solución numérica es:
Una relación de convergencia con respecto a la fase de onda se define de la siguiente manera:
o igualmente:
en la cual σΔx = resolución espacial. Debido a σ = 2π/L, en la cual L es la longitud de onda sinusoidal, se deduce lo siguiente:
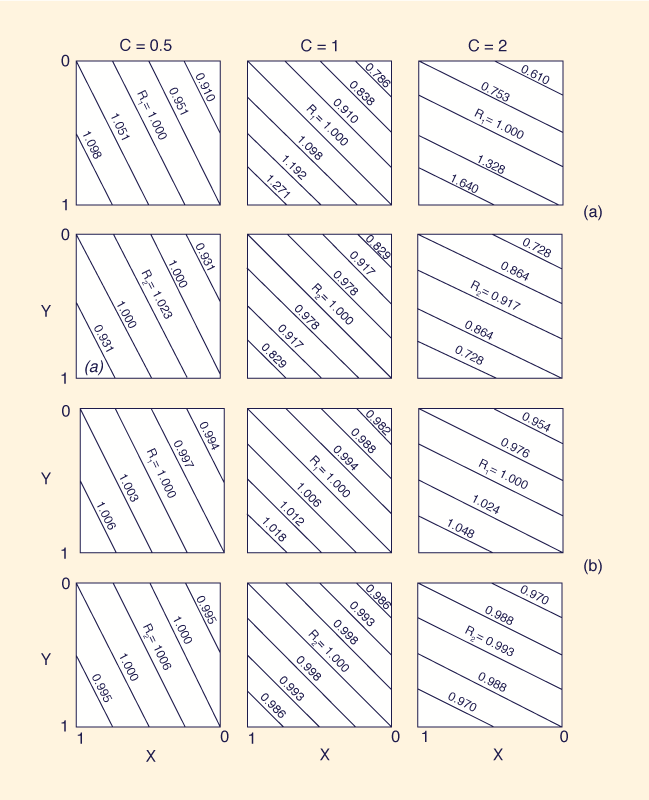
en la cual L / Δx = número de intervalos discretos de espacio por longitud de onda sinusoidal. Ambos R1 y R2 son funciones de X, Y, C, y L / Δx. La Figura 2 muestra la variación de R1 y R2 como una función de X, Y, C, y L / Δx. Se pueden obtener las siguientes conclusiones:
La inestabilidad, R1 > 1, del Esquema I (Tabla I) para números de Courant > 1, y del Esquema II para números de Courant < 1, es confirmada. Asimismo, se confirma la estabilidad incondicional y una mayor dispersión numérica del Esquema III.
5. PROPIEDADES DE ESTABILIDAD Y CONVERGENCIA
Ecuación lineal con coeficiente constante. En este caso, la velocidad convectiva u es constante en el espacio y el tiempo. La solución numérica usando las Ecs. 3-6 con X = Y = 1/2 y Ecuación lineal con coeficiente variable. En este caso, la velocidad convectiva u varía en el espacio y el tiempo. Por lo tanto, el número de Courant varía de una celda a la siguiente. El análisis de estabilidad lineal de von Neumann muestra que la relación de convergencia (amplitud de onda) R1 es igual a 1 para X = Y = 1/2 y para todos los valores de C. Sin embargo, la relación de convergencia (fase de onda) R2 es igual a 1 solo para C = 1. Para números de Courant diferentes de uno, siempre habrá una cierta cantidad de error de fase. La estabilidad del esquema requiere que μ ≥ 0; por otra parte, la convergencia de la amplitud de la onda mejora a medida que μn → 0. Usando la Ec. 9, se pueden formular varios esquemas explícitos de segundo orden, incondicionalmente estables pero precisos. Las propiedades numéricas de tres de estos esquemas se dan en la Tabla 2. Los Esquemas IV y V pueden considerarse como generalizaciones de los Esquemas I y II, respectivamente, para el caso de números de Courant variables. Sin embargo, a diferencia de los esquemas I y II, los esquemas IV y V no difusionan numéricamente la amplitud de onda. El esquema VI, un esquema centrado en el espacio y el tiempo, tiene una precisión de segundo orden para todos los valores de C. Para valores fijos de X y Y, el error de segundo orden de los Esquemas IV a VI será directamente proporcional a | 1 - C |. Asimismo, para valores fijos de X, Y y C (C ≠ 1), el error de segundo orden será directamente proporcional a ∂3ζ /∂x3. La equivalencia de los Esquemas IV a VI se puede demostrar sustituyendo los valores de X y Y de la Tabla 2 en las Ecs. 4-6. Esto lleva a:
y
para los tres esquemas. Además, para C = 1, C2 = C3 = 0, y ζ j + 1 n + 1 = ζj n, es decir, la cantidad ζ está siendo sometida a convección pura. Para C ≠ 1 se introduce un efecto dispersivo porque el cálculo de ζ j + 1 n + 1 se basa no solamente en ζj n sino también en ζj n + 1 y ζj + 1 n . 6. EJEMPLO ILUSTRATIVO
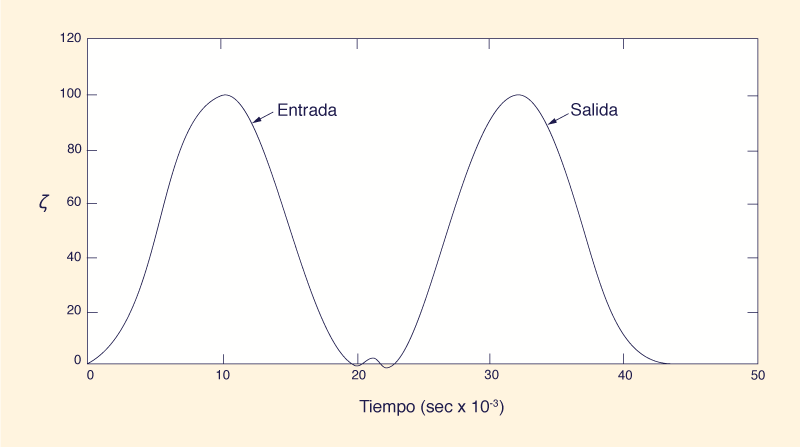
Se estableció un ejemplo hipotético para demostrar las propiedades numéricas de los esquemas descritos en la Tabla 2. Un canal de 20,000 pies de largo se dividió en 20 tramos de Δx = 1,000 pies Los resultados de la simulación se muestran en la Fig. 3. La estabilidad, la convergencia de la amplitud de la onda y la conservación de la masa se mantienen para todos los números de Courant. Como era de esperar, se detectó una pequeña cantidad de ruido numérico.
Esto es causado por los errores de segundo orden y tiende a concentrarse en las regiones de cambios bruscos en ∂3ζ /∂x3 (o ∂3ζ /∂t 3).
El error numérico es una función de | 1 - C | y desaparece conforme
7. RESUMEN Se presenta un tratamiento teórico unificado de las propiedades numéricas de una clase de esquemas explícitos de la ecuación de convección pura. Para los casos de números de Courant que varían lentamente, la teoría se usa para mostrar que la estabilidad incondicional y la precisión de segundo orden pueden lograrse dentro del marco de una formulación explícita. APÉNDICE I. BIBLIOGRAFÍA
APÉNDICE II. SIMBOLOGÍA C = número de Courant; C1 = coeficiente, Ec. 4; C2 = coeficiente, Ec. 5; C3 = coeficiente, Ec. 6; j = índice de discretización espacial; L = longitud de onda; M = parámetro, Ec. 16; N = parámetro, Ec. 17; n = índice de discretización de tiempo; P = parámetro, Ec. 18; p = cos (σΔx); q = sin (σΔx); R = error de aproximación; Además, parámetro, Ec. 13; R1 = relación de convergencia de amplitud de onda; R2 = relación de convergencia de la fase de onda; S = parámetro, Ec. 14; u = velocidad media; μn = velocidad de fase de la solución numérica; X = factor de ponderación de la derivada temporal; Y = factor de ponderación de la derivada espacial; βI = factor de amplificación (o atenuación); βR = frecuencia de onda; Δt = incremento temporal; Δx = incremento espacial; ζ = alguna cantidad física a ser convectada; μn = coeficiente de difusión numérica, Ec. 9; y σ = número de onda.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 220525 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |