Cornish (1907)

Foto temprana de un evento de ondas de rollo en los Alpes suizos.


LOS ESTADOS DE FLUJO


Víctor M. Ponce

Profesor Emérito de Ingeniería Civil y Ambiental

Universidad Estatal de San Diego, California


27 noviembre 2023

RESUMEN.  Se presentan, explican y comparan cuatro números adimensionales en el flujo en canales abiertos. Dos de ellos son relaciones de velocidades y los otros dos son relaciones de difusividades. Juntos, estos cuatro números completan la descripción del estado del flujo, ya sea para flujo permanente (los dos primeros) o flujo no permanente (los dos últimos).

1.  INTRODUCCIÓN

Hay dos propiedades características del flujo en canales abiertos: (1) velocidad; y (2) difusividad. La velocidad de una porción de fluido es la tasa de cambio de su posición en el espacio, en una dirección determinada, con el tiempo. La unidad de velocidad es L/T, en la cual L = longitud y T = tiempo. La expresión u = 1 m/s (un metro por segundo) describe el hecho de que una porción de fluido se mueve a lo largo de una dirección o trayectoria de flujo establecida, con una velocidad u igual a 1 metro por segundo. En mecánica de fluidos, la velocidad se relaciona con el proceso de convección de una porción de fluido; en hidrología, se relaciona con la concentración, un concepto relacionado con el tiempo de concentración. En los modelos matemáticos hidráulicos e hidrológicos, la velocidad de convección se describe mediante una ecuación diferencial de primer orden.

La difusividad ν de un flujo superficial es el primer momento de la velocidad. Las unidades de difusividad son (L/T)L, o su equivalente L2/T. La expresión ν = 1 m2/s, en relación con una perturbación dada, describe la certeza de que la perturbación se está propagando a la velocidad controlada por el coeficiente de difusividad ν. En mecánica de fluidos, la difusividad se relaciona con el proceso de difusión; en hidrología, se relaciona con la atenuación o disipación de una onda de inundación. En los modelos matemáticos hidráulicos e hidrológicos, la difusividad se describe mediante una ecuación diferencial de segundo orden (Tabla 1).

Tabla 1.  Velocidades y difusividades en el flujo en canales abiertos.
Propiedad Símbolo Unidades Proceso Orden
VelocidaduL/T Convección Primer
Difusividad ν L2/T DifusiónSegundo

Estas propiedades de un fluido, velocidad y difusividad, caracterizan el flujo hasta el segundo orden. Se pueden plantear varios tipos de velocidades y difusividades, y sus proporciones constituyen los parámetros adimensionales denominados "números". Estos últimos resumen las propiedades del flujo, mejorando su comprensión tanto en condiciones de flujo permanente como no permanente. Este hecho se refleja en el título del presente artículo: Los estados de flujo, refiriéndose a los diversos estados bajo los cuales se puede describir el flujo utilizando estos números. El resto de este artículo explica los números, aclarando su definición y alcance.

2.  VELOCIDADES EN FLUJO EN CANALES ABIERTOS

Hay tres velocidades características en el flujo en canales abiertos: (1) la velocidad media u del flujo permanente; (2) la celeridad relativa v de la onda cinemática; y (3) la celeridad relativa w de la onda dinámica. En el flujo no permanente, celeridad es la velocidad de una onda, en contraposición a la velocidad del flujo permanente (Ponce, 1991).

La celeridad de una onda cinemática es: ck = β u, en la que cual β = exponente de la curva de gasto Q = αAβ, con Q = caudal, A = área de flujo, y α = coeficiente. Por lo tanto, la celeridad relativa de la onda cinemática es: v = ck - u, es decir, la velocidad de la onda cinemática relativa al flujo (Ponce, 2014a).

La celeridad de una onda dinámica, la cual tiene dos componentes, es: cd = u ± (gD)1/2, en la cual g = aceleración gravitacional, D = profundidad hidráulica, con D = A/T, y T = ancho superior del canal o corriente. Por lo tanto, la celeridad relativa de la onda dinámica es: w = cd - u = ± (gD)1/2, es decir, la velocidad de una onda dinámica relativa al flujo (Ponce, 2014b).

Las tres velocidades identificadas aquí abarcan tanto el flujo permanente (u) como el flujo no permanente (v y w), así como ondas largas (cinemáticas, v), y ondas cortas (dinámicas, w). Observamos que éstas son las únicas velocidades que se pueden identificar en el presente contexto.

3.  DIFUSIVIDADES EN FLUJO EN CANALES ABIERTOS

Se reconocen tres difusividades en el flujo en canales abiertos: (1) difusividad molecular; (2) difusividad hidráulica; y (3) difusividad espectral. En mecánica de fluidos, la difusividad molecular νm se conoce comúnmente como viscosidad cinemática ν, una medida de la resistencia interna del fluido a nivel molecular. En el flujo no permanente en canales abiertos, la difusividad hidráulica se expresa en términos de la pendiente de fondo y la fricción de fondo. En el flujo no permanente en canales abiertos, la difusividad espectral se define en términos de la longitud de onda de la perturbación sinusoidal. Estas proposiciones se detallan en el Cuadro A.

Cuadro A.  Difusividades en el flujo en canales abiertos.

  1. Ley de viscosidad de Newton: τ /ρ = ν (∂u/∂s), en la cual τ = esfuerzo cortante, ρ = densidad (de masa) del fluido, ν = viscosidad cinemática del fluido, y (∂u/∂s) = gradiente de velocidad en la dirección s perpendicular a la dirección del esfuerzo cortante τ.

  2. τ /ρ = νm (∂u/∂s), en la cual νm = difusividad molecular.

  3. La difusividad molecular νm puede expresarse como νm = u (Lm /2), en la cual Lm = (2νm /u)  es una longitud molecular característica (Chow, 1959).

  4. La difusividad hidráulica νh se define como νh = u (Lo /2), en la cual Lo = (do /So) es la longitud hidráulica característica del tramo, definida como la distancia, a lo largo del canal, en la cual el flujo pierde una altura igual a la profundidad (de equilibrio) (Hayami, 1951; Ponce and Simons, 1977).

  5. La difusividad espectral νs se define como νs = u (L/2), en la cual L = longitud característica de la perturbación sinusoidal (Ponce, 1979).

  6. Téngase en cuenta que las tres difusividades, molecular, hidráulica y espectral, se definen en términos de sus respectivas longitudes características: (1) longitud molecular, (2) longitud hidráulica, y (3 ) longitud espectral. Además, nótese que las tres difusividades comparten una estructura matemática similar: El producto de la velocidad convectiva por la mitad de la respectiva longitud característica.

4.  RELACIÓN DE VELOCIDADES EN FLUJO PERMANENTE:  NÚMERO DE FROUDE

El número de Froude es la relación entre la velocidad media del flujo u y la celeridad relativa de las ondas dinámicas w:  F = u/w (Ponce, 2014b). Este número compara la velocidad media del flujo con la celeridad relativa de perturbaciones superficiales pequeñas; de esta manera, clasifica al flujo en tres tipos: (1) subcrítico, para F < 1; (2) crítico, para F = 1; y supercrítico, para F > 1.

En la hidráulica de canales abiertos, el número de Froude es útil para determinar la dirección de cálculo en el análisis de los perfiles de la superficie del agua: Hacia aguas arriba para flujo subcrítico, y aguas abajo para flujo supercrítico. En hidráulica fluvial, el número de Froude es una indicación del límite entre el régimen inferior, F < 0,5, generalmente en el cual predominan las ondulaciones y las dunas en el lecho, y el régimen superior, F > 0,5, en el cual prevalecen los lechos planos y las antidunas (Simons y Richardson, 1966).

[Haga click encima de la figura para desplegar]
Simons y Richardson (1966).

Fig. 1   Formas de rugosidad de fondo en canales aluviales: (a) régimen inferior (izquierda), y
(b) régimen superior (derecha).

Nótese la marcada división entre flujo subcrítico y supercrítico para F = 1. Este último constituye efectivamente un punto singular, en el cual la dirección de cálculo cambia instantáneamente entre hacia aguas arriba y hacia aguas abajo. La existencia de una singularidad para F = 1 puede hacer que el cálculo sea inestable; por lo tanto, se recomienda precaución en las proximidades del flujo crítico. Una historia del número de Froude, incluidas las importantes contribuciones de Froude a la hidráulica, ha sido presentada por Ponce (2014b).

5.  RELACIÓN DE DIFUSIVIDADES EN FLUJO PERMANENTE:  NÚMERO DE REYNOLDS

El número de Reynolds es una relación de viscosidades o difusividades. El número de Reynolds convencional, definido para una forma de sección transversal arbitraria, en términos de radio hidráulico Ro, es: R = (uo Ro)/νm (Ponce, 2014b). Para un canal hidráulicamente ancho: R = (uo do)/νm. Para los propósitos de este artículo, definimos un número de Reynolds alternativo como una relación apropiada de difusividades, de la siguiente manera: R' = νh/νm. Por lo tanto: R' = R/(2So) (ver Tabla 2).

El número de Reynolds R clasifica al flujo en uno de los siguientes regímenes: (1) laminar, (2) transicional, o (3) turbulento. En flujo en canales abiertos, en condiciones de flujo permanente, se produce flujo laminar para R ≤ 500; flujo turbulento para R > 2000; y flujo transicional en el rango intermedio (500 < R ≤ 2000). El uso del número de Reynolds es algo limitado en el flujo en canales abiertos, ya que el flujo usualmente permanece en el régimen turbulento.

6.  RELACIÓN DE VELOCIDADES EN FLUJO NO PERMANENTE:  NÚMERO DE VEDERNIKOV

El número de Vedernikov es la relación entre la celeridad relativa de la onda cinemática v y la celeridad relativa de la onda dinámica w: V = v /w (Ponce, 2014b). Este número caracteriza los siguientes estados de flujo:

  • V < 1:  Flujo estable, para v < w,

  • V = 1:  Flujo neutralmente estable, para v = w,

  • V > 1:  Flujo inestable, para v > w.

Bajo flujo estable, la celeridad relativa de la onda cinemática v es menor que la celeridad relativa de la onda dinámica w; por lo tanto, las perturbaciones u ondas superficiales se atenúan.

Bajo flujo neutralmente estable, la celeridad relativa de la onda cinemática v es igual a la celeridad relativa de la onda dinámica w; por lo tanto, las perturbaciones o ondas superficiales no se atenúan ni se amplifican.

Bajo flujo inestable, la celeridad relativa de la onda cinemática v es mayor que la celeridad relativa de la onda dinámica w; por lo tanto, las perturbaciones o ondas superficiales se amplifican, es decir, experimentan una atenuación negativa. En la práctica, la condición V > 1 lleva al desarrollo de ondas de rollo o pulsantes, reconocidas como un tren de ondas que se trasladan aguas abajo, usualmente en canales empinados y revestidos (Fig. 2). La condición de flujo que produce las ondas de rollo se explica en base a que la onda cinemática, la cual transporta masa, sobrepasa a la onda dinámica, la cual transporta energía (Craya, 1952; Ponce y Choque Guzman, 2019).

 

Fig. 2   Un evento de ondas de rollo en un canal lateral de la irrigación
Cabana-Mañazo, Puno, Perú.

El número de Vedernikov (Vedernikov, 1945; 1946), originalmente denominado así por Powell (1948) y posteriormente presentado por Chow (1959) en el Capítulo 8 de su libro de texto, fue elucidado un tiempo después por Ponce (1991), quien expresó el número de Vedernikov en términos de las celeridades relativas de las ondas cinemáticas y dinámicas. El tema del control de ondas de rollo en ríos canalizados ha sido extensamente tratado por Ponce y Choque Guzman (2019).

7.  RELACIÓN DE DIFUSIVIDADES EN FLUJO NO PERMANENTE:  NÚMERO DE ONDA ADIMENSIONAL DE PONCE-SIMONS

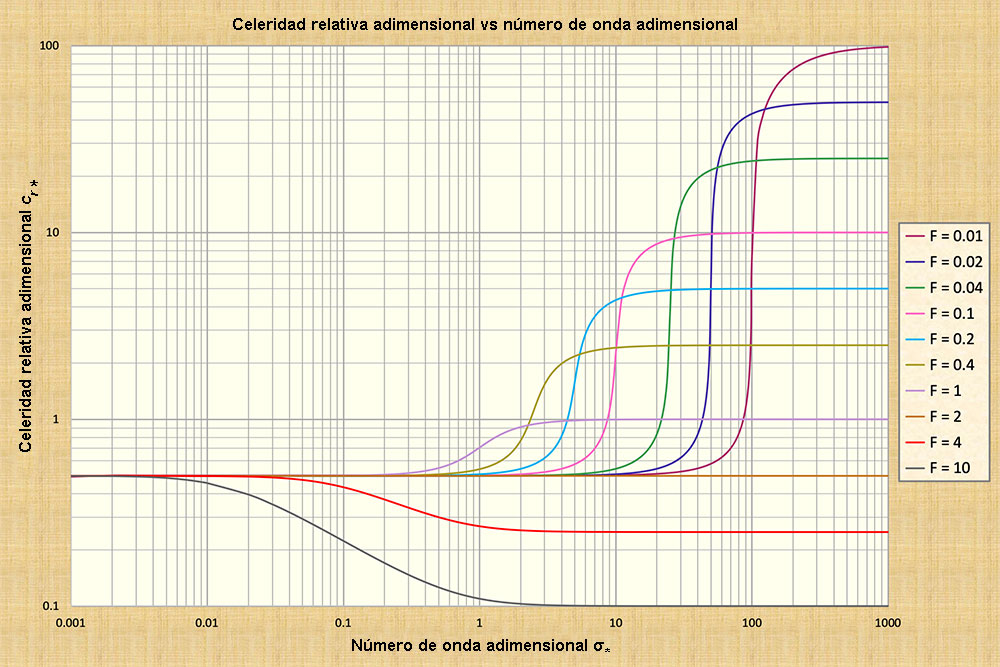
El número de onda adimensional de Ponce y Simons (1977) se define como sigue: σ* = (2π /L)Lo. También puede ser expresado como una relación de difusividades: σ* = (2π /L)Lo = 2π (νh/νs). El número de onda adimensional σ* clasifica el flujo no permanente en cuatro rangos espectrales (Fig. 3):

  1. Cinemático (al extremo izquierdo),

  2. Difusivo (a la izquierda del centro),

  3. Cinemático-dinámico mixto (centro-derecha), y

  4. Dinámico (derecho a extremo derecho).

Los dominios precisos de estos rangos han sido calculados por Ponce (2023):

  • Flujo cinemático: σ* < 0.001.

  • Flujo difusivo: 0.001 ≤ σ* < 0.17.

  • Flujo cinemático-dinámico mixto: 0.17 ≤ σ* < 1 a 100, dependiendo del número de Froude (referirse a la Fig. 3).

  • Flujo dinámico: σ* ≥ 10 a 1000, dependiendo del número de Froude (referirse a la Fig. 3).

Ponce y Simons (1977)

Fig. 3   Celeridad relativa adimensional cr* vs número de onda adimensional σ*.

Los hallazgos de Ponce y Simons (1977) ayudan a elucidar el comportamiento de todos los tipos de ondas posibles en el flujo no permanente en canales abiertos. Estas últimas incluyen tanto ondas "largas", de naturaleza cinemática, en el extremo izquierdo de la Fig. 3, como ondas "cortas", de naturaleza dinámica, en el extremo derecho. También se incluyen las ondas difusivas, en el rango intermedio, las cuales presentan propiedades bastante prácticas, y las ondas cinemático-dinámicas mixtas, es decir, las ondas mixtas, en el rango central a derecho. Estas ondas mixtas son, en su mayor parte, poco prácticas debido a su extremadamente fuerte tendencia disipativa (Ponce, 2023).

8.  RESUMEN

Se presentan, explican y comparan cuatro números adimensionales en el flujo en canales abiertos (Tabla 2). Dos de ellos son relaciones de velocidades y los otros dos de difusividades. Los cuatro números se definen en términos de cantidades físicas, ya sean velocidades o difusividades. Tomados en conjunto, estos números completan la descripción del estado de flujo, ya sea para flujo permanente (los dos primeros números) o no permanente (los dos últimos).

Tabla 2.  Números adimensionales en el flujo en canales abiertos.
Número adimensional Símbolo Relación de Definición Rango Alternativo
FroudeFVelocidades u / w (a) subcrítico,
(b) crítico,
(c) supercrítico		Ninguno
ReynoldsR'Difusividades νh /νm (a) laminar,
(b) transicional,
(c) turbulento		R
VedernikovV Velocidades v / w(a) estable,
(b) neutral,
(c) inestable		Ninguno
Ponce-Simons σ*Difusividades 2π (νh /νs) (a) cinemático,
(b) mixto,
(c) dinámico		Ninguno

BIBLIOGRAFÍA

Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York, NY.

Cornish, V. 1907. Progressive waves in rivers. Journal of the Royal Geographical Society, Vol. 29, No. 1, January, 23-31.

Craya, A. 1952. The criterion for the possibility of roll wave formation. Gravity Waves, National Bureau of Standards Circular No. 521, National Bureau of Standards, Washington, D.C. 141-151.

Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December, Extract.

Ponce, V. M. y D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering ASCE, 103(12), 1461-1476.

Ponce, V. M. 1979. On the classification of open channel flow regimes. Proceedings, Fourth National Hydrotechnical Conference, Vancouver, British Columbia, Canada.

Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.

Ponce, V. M. 2014. Fundamentals of Open-channel Hydraulics. Online text.

Ponce, V. M. y B. Choque Guzman. 2019. The control of roll waves in channelized rivers. Online article.

Ponce, V. M. 2023. When is the diffusion wave applicable? Online article.

Powell, R. W. 1948. Vedernikov's criterion for ultra-rapid flow. Transactions, American Geophysical Union, Vol. 29, No. 6, 882-886.

Simons, D. B. y E. V. Richardson. 1966. Resistance to flow in alluvial channels. Geological Survey Professional Paper 422-J, U.S. Government Printing Office, Washington, D.C.

Vedernikov, V. V. 1945. Conditions at the front of a translation wave disturbing a steady motion of a real fluid. Doklady Akademii Nauk USSR, 48(4), 239-242.

Vedernikov, V. V. 1946. Characteristic features of a liquid flow in an open channel. Doklady Akademmi Nauk USSR, 52(3), 207-210.

231127