1.  INTRODUCCIÓN

Las represas brindan varios beneficios a la sociedad. Sin embargo, las inundaciones causadas por fallas en las represas han producido algunos de los desastres más devastadores de los últimos dos siglos [20]. Como resultado, la falla de las represas de tierra se ha convertido en un tema de preocupación entre ingenieros, funcionarios federales, estatales y locales, y la sociedad en general.

Existe una amplia documentación sobre roturas de presas y los mecanismos están bien comprendidos. Sin embargo, las relaciones causales no son tan claras. Los estudios han demostrado que las fallas de las presas de tierra pueden deberse a varias causas. Generalmente, éstas se clasifican de la siguiente manera: (a) hidrológicas, y (b) geotécnicas.

La falla generalmente da como resultado el desarrollo eventual de una brecha que compromete una cierta longitud del terraplén. El ancho de brecha ha sido documentado en un gran número de casos. Los estudios de ruptura de presas han demostrado que la forma y la evolución temporal de la ruptura determinan en gran medida las características del hidrograma de salida [12].

El objetivo de este artículo es desarrollar una relación adimensional entre los parámetros geométricos e hidráulicos que gobiernan la ruptura de una presa de tierra. Para ello se definen los siguientes parámetros geométricos e hidráulicos:

• Profundidad máxima de la brecha, D_b.

• Ancho superior de la brecha, W_b.

• Caudal pico de salida de la brecha, Q_p.

• Tiempo de falla de la brecha, t_f.

• Altura máxima de la represa, H_d.

• Ancho superior de la represa, W_d.

• Volumen del reservorio, V_r.

• Longitud característica del reservorio, L_r.

2.  ESTUDIOS DE CASOS DE FALLAS DE RUPTURA DE PRESAS

Se dispone de información valiosa de fallas documentadas de ruptura de presas. Wahl [2] ha identificado varias ecuaciones de predicción de brechas. Estas ecuaciones se han basado en análisis de estudios de casos que comprenden de 20 a 60 fallas. Las fuentes de datos de estudios de caso para represas que han fallado son numerosas, por ejemplo, Ponce [12], Singh [17] y Wahl [2]. Varias de las fallas ocurrieron antes de que se reconociera la necesidad de documentar completamente el proceso de rotura y sus características relacionadas.

Babb y Mermel [1] resumieron más de 600 incidentes en represas en todo el mundo. Sin embargo, en la mayoría de los casos faltaba información detallada y de alta calidad. Durante la década de 1980, varios investigadores compilaron bases de datos de estudios de casos bien documentados, en un esfuerzo por desarrollar relaciones predictivas para los picos de salida de brechas [3, 5, 6, 7, 10, 12, 14, 16, 18].

Wahl [20] realizó una investigación bibliográfica para generar una única base de datos que contuviera todos los estudios de casos citados, con un total de 108 fallas de terraplenes. El tipo, la cantidad y la calidad de los datos disponibles para los estudios de casos individuales variaron ampliamente. Hay muchos casos de discrepancias significativas entre datos similares reportados por diferentes investigadores.

Los investigadores han propuesto un número de relaciones para estimar los parámetros de brecha y los picos de salida. El efecto de los parámetros de ruptura en la descarga máxima y el tiempo de evacuación se ha reportado en la literatura. La descarga máxima fue examinada por Singh y Snorrason [15]. Petrascheck y Sydler [11] demostraron la sensibilidad del caudal de salida máximo, el nivel de inundación y el tiempo de llegada de la inundación, a los cambios en el ancho de la brecha y el tiempo de formación. La forma y la evolución temporal de la brecha, junto con el tamaño de la presa y del embalse, determinan en gran medida las características del hidrograma de salida durante la ruptura. Singh y Snorrason [14] proporcionaron la primera guía cuantitativa sobre el ancho de la brecha al trazar el ancho de la brecha vs la altura de la presa para veinte fallas de presas.

MacDonald y Langridge-Monopolis [10] relacionaron el tiempo de ruptura hasta la falla con el volumen de material erosionado. El volumen de material erosionado se relacionó con el factor de formación de la brecha, definido como el producto del volumen de salida por la profundidad inicial del agua sobre el fondo de la brecha.

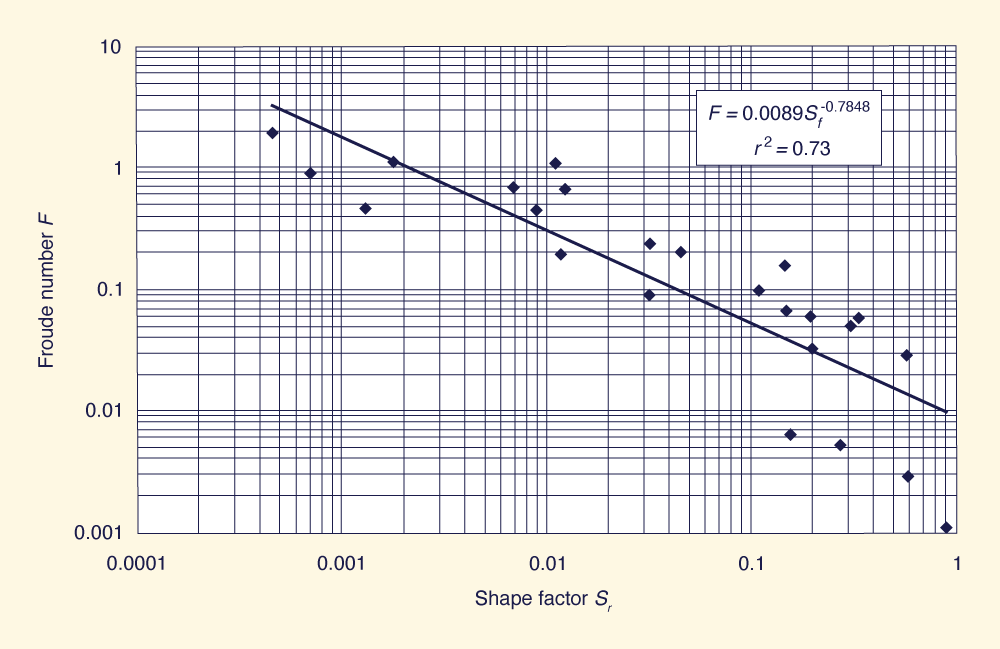
Froehlich [5] desarrolló ecuaciones de predicción adimensionales para estimar el ancho promedio de la brecha, el factor de pendiente lateral promedio, y el tiempo de formación. Las predicciones de Froehlich se basaron en las características de la presa, incluido el volumen del embalse, la profundidad del agua sobre el fondo de la brecha, la profundidad del tramo, la longitud del terraplén en la cresta de la presa, el ancho del fondo de la brecha, los coeficientes empíricos que explican el desbordamiento vs fallas sin rebosamiento, y la presencia o ausencia de una pared central. Singh y Snorrason [14, 15] presentaron relaciones para el caudal máximo en función de la altura de la presa y el almacenamiento del embalse.

Froehlich [6] desarrolló una ecuación de regresión para la predicción del caudal máximo basado en el volumen del embalse y la carga hidráulica. Usó datos de 22 estudios de casos para los que se disponía de flujos de salida máximos. Harris y Wagner [8] aplicaron la ecuación de transporte de sedimentos de Schoklitsch a los caudales, durante la ruptura de presas. Lou [9] y Ponce y Tsivoglou [13] desarrollaron un modelo que vinculaba la ecuación de transporte de sedimentos de Meyer-Peter y Muller con las ecuaciones diferenciales unidimensionales del flujo no permanente de agua y sedimentos.

Walder y O'Connor [19] presentaron un modelo basado en la física de la formación de brechas en una presa, y lo usaron para relacionar el flujo de salida máximo adimensional con un parámetro adimensional que contiene una caída en el nivel del embalse, el volumen de agua liberada, y la tasa de erosión vertical media de la presa. Fread [4] usó un enfoque paramétrico para encontrar el hidrograma de salida de la brecha, usando observaciones empíricas de fallas. Usó principios hidráulicos para la predicción del flujo de salida de la brecha.

Ponce [12] definió un número de Froude basado en el flujo máximo de salida de la brecha y lo relacionó con un factor de forma definido de la siguiente manera:

S = (W_bD_b) / (W_dH_d)

El resultado mostró una tendencia definida a una relación inversa, la cual se muestra en la Fig. 1. Los resultados de Ponce fueron muy similares a los reportados por Black [2]. Sin embargo, ambas relaciones muestran un ajuste pobre a los datos observados.

Fig. 1  Número de Froude F vs factor de forma S.

3.  ANÁLISIS DE LOS DATOS

Se hizo una comparación entre los datos de Ponce y la base de datos de la Oficina de Seguridad de Represas [20]. Se determinó que sólo 24 casos reportados por Wahl [2] son útiles para este estudio. Aparentemente, éstos son los mismos que los informados por Ponce [12]. Una revisión del trabajo de Ponce indica que fue recopilado directamente de fuentes originales. Por esta razón, se prefiere su uso en este estudio. Los datos mencionados se muestran en la Tabla 1.

Tabla 1.  Características físicas y datos de brecha usados en este estudio. Represa / Reservorio Vr Qp tf Wb Db Wd Hd F S Sf Represa Neek Run PA, U.S. 4.93×104 9.2 3 30.48 7 63 7 0.0052 0.4838 0.27265 Represa Lago Avalon NM, U.S. 7.77×104 2321.9 2 137.16 14.63 420.6 14.63 0.0966 0.3261 0.10862 Represa Sherburne NY, U.S. 7.52×104 14.2 3 45.72 10.36 91.44 10.36 0.0029 0.5000 0.57595 Represa Dells WI, U.S. 1.3×107 5434.9 0.67 112.77 17.98 292.61 17.98 0.2018 0.3854 0.04563 Represa Hatfield WI, U.S. 1.22×107 3397.9 2 91.44 6.7 137.16 6.7 0.6841 0.6667 0.00633 Arroyo Horse Denver, CO, U.S. 2.09×107 3883.2 3 60.96 12.8 182.88 16.76 0.4441 0.2545 0.000894 Represa Hatchtown Salt Lake City UT, U.S. 1.48×107 1970.8 4 36.57 19.8 237.74 19.81 0.1953 0.1538 0.01164 Represa del Arroyo Goose SC, U.S. 1.06×107 492.7 12 30.48 3.96 701.04 6.09 0.6549 0.0282 0.01228 Represa Mammoth SC, U.S. 1.35×107 2520.1 3 9.14 21.34 48.77 21.34 0.8929 0.1874 0.00071 Puddingstone SC, U.S. 6.16×105 283.2 3 91.44 10.67 251.46 15.24 0.0284 0.2546 0.56886 Represa Hemet CA, U.S. 8.63×106 1600 3 30.48 6.09 83.21 6.09 1.1135 0.3663 0.00791 Represa Ciudad Elk OK, U.S. 7.4×105 608.79 0.83 45.72 9.14 259.08 9.14 0.1538 0.1764 0.1463 Represa Arroyo Sinker ID, U.S. 3.33×106 926 2 91.44 21.34 335.28 21.34 0.0328 0.2727 0.19646 Represa Frenchman MT, U.S. 8.64×106 1602.68 3 243.84 12.19 884 12.19 0.0493 0.2758 0.30412 Represa Baldwin Hills Res, CA, U.S. 1.11×106 141.58 4.5 121.92 48.77 167.64 148.77 0.0011 0.7272 0.89801 Lago Latonka Mercer PA, U.S. 1.59×106 294.48 3 33.53 13.11 701 13.11 0.0591 0.0478 0.1938 Represa Nanaksagar India 2.1×108 9709.5 12 45.72 15.85 3218.68 15.85 1.0745 0.0142 0.01111 Brook NH, U.S. 5.18×103 70.79 3 6.4 6.1 137.16 18.9 0.2344 0.0151 0.03203 Represa del Lago Knife MN, U.S. 9.86×105 1098.66 5 12.19 6.096 60.96 6.096 1.91 0.2000 0.00046 Represa Teton ID, U.S. 3.08×108 46786.5 4 45.72 79.55 945 92.96 0.4605 0.0414 0.01304 Represa Euclides da Cunha Brasil 1.36×107 1005.2 7.25 131.06 53 304.8 53 0.0063 0.4300 0.15567 Armando de Salle Oliveira Brasil 2.59×107 7195 2 167.64 35 660 35 0.0662 0.2540 0.14952 Lago Kelly Barnes Toccoa, GA, U.S. 4.93×105 549 0.5 137.16 7.92 152.4 7.92 0.0573 0.9000 0.33581 Represa Franfurt Germay 3.51×105 79.28 2.5 9.45 9.75 120 9.75 0.0879 0.0787 0.0315

En este estudio se utilizó el número de Froude del caudal de salida pico:

Qp            F  =  _______________            (Wb)(gDb3)1/2

(1)

en el cual g = aceleración de la gravedad.

Un nuevo factor de forma S_ƒ es definido de la siguiente manera:

WbWdHd            Sƒ  =  _____________                    Vr

(2)

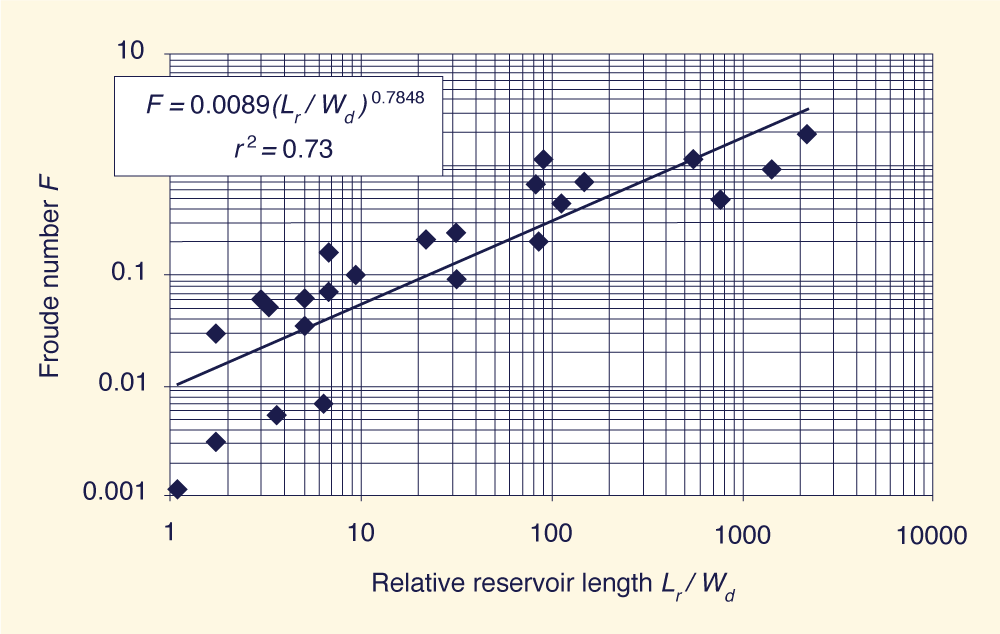
Un análisis de la relación entre el número de Froude del flujo de salida pico y el nuevo factor de forma S_ƒ, basado en todos los datos disponibles, condujo a los gráficos que se muestran en las Figs. 2 y 3. La relación es:

F  = 0.0089 Sƒ-0.7648

(3)

con un coeficiente de determinación r ² = 0.73.

Fig. 2  Número de Froude F vs factor de forma Sƒ.

De acuerdo con la Figura 3, hay dos tendencias limitantes:

1. Cuando S_ƒ → 0, F aumenta por encima de 1. Para F = 1, el factor de forma S_ƒ = 0.00208. La relación V_r / (W_dH_d) puede tomarse como la longitud característica del embalse L_r. Entonces, el nuevo factor de forma se puede expresar como sigue: S_ƒ = W_b / L_r. Por lo tanto, cuando L_r ≥ 480W_b, F ≥ 1. Con base en los datos disponibles de casos de falla de presas (ver Tabla 1), es posible mostrar la variación de L_r / W_b vs el número de Froude F, como se muestra en la Fig. 4. Esta figura muestra que F y L_r están directamente relacionados.

2. Cuando S_ƒ → 1, F → 0. En otros trabajos, cuando L_r = W_b, F → 0. En esta condición, no hay flujo que crearía una inundación peligrosa.

Fig. 3  Número de Froude F vs factor de forma Sƒ.

Fig. 4  Variación de F vs Lr /Wb.

4.  CONCLUSIONES

Según los datos disponibles, parece haber una buena correlación entre el número de Froude del caudal pico de salida F y el nuevo factor de forma S_ƒ. Además, la longitud característica del embalse L_r es un indicador de la cantidad de agua responsable de la magnitud de los caudales máximos durante la rotura de una presa. En otras palabras, cuando L_r aumenta y/o W_r disminuye, F también aumenta.

BIBLIOGRAFÍA

1. BABB, A. O. y T. W. MERMEL. 1968. "Catalog of dam disasters, failures and accidents", Bureau of Reclamation, Washington, DC, US.

2. BLACK, E. B. 1925. "Partial failure of earth dam at Horton, Kansas", Engineering News Record, 1925, 95(2), pp58-60.

3. COSTA, J. E. 1985. "Flood from dam failures", U.S. Geological Survey Open-file Report 85-560, Denver, CO, US, 54p.

4. FREAD, D. L. 1988. "Breach: an erosion model for earthen dam failures", 1988, NWS Report, National Oceanic & Atmospheric Administration, Silver Spring, MD, US, (revised 1991).

5. FROEHLICH, D. C. 1987. "Embankment dam breach parameters", Proceedings of the ASCE National Conference on Hydraulic Engineering, 3-7 August,, Williamsburg, VA, US, pp570-575.

6. FROEHLICH, D. C. 1995. "Peak outflow from breached embankment dam", Proceedings of the ASCE Conference on Water Resources Engineering, 14-18 August 1995(a), San Antonio, TX, US, pp887-89I.

7. FROEHLICH, D. C. 1995. "Embankment dam breach parameters revisited", Journal of Water Resources Planning & Management, 121(1), pp90-97.

8. HARRIS, G. W., y WAGNER, D. A. 1967. "Outflow from breached earth dams", 1967, University of Utah, Salt Lake City, UT, US.

9. LOU, W. C, 1981. "Mathematical modelling of earth dam breaches", Thesis, 1981, presented to Colorado State University, Fort Collins, CO, US (in partial fulfilment of requirements for the Degree of Doctor of Philosophy).

10. MACDONALD, T. C., y J. L. MONOPOLIS. 1984. "Breaching characteristics of dam failures", Journal of Hydraulic Engineering, 110 (5), pp567-586.

11. PETRASCHECK, A. W., y P. A. SYDLER. 1984. "Routing of dam break flood", International Water Power & Dam Construction, 36, pp29-32.

12. PONCE, V. M. 1982. "Documented cases of earth dam breaches", 1982, San Diego State University, SDSU Civil Engineering Series, No 82149.

13. PONCE, V. M., y A. J. TSIVOGLOU. 1981. "Modelling gradual dam breaches", Journal of the Hydraulics Division, ASCE, 107(7), pp829-838.

14. SINGH, K. P., y A. SNORRASON. 1982. "Sensitivity of outflow peaks and flood stage to the selection of dam breach parameters and simulation models", Journal of Hydrology, 68, 295-310.

15. SINGH, K. P. y A. SNORRASON. 1984. "Sensitivity of outflow peaks and flood stage to the selection of dam breach parameters and simulation models", SWS Contract Report 288, Illinois Department of Energy & Natural Resources, State Water Survey Division, Surface Water Section, University of Illinois, US, 179p.

16. SINGH, K. P., y P. D. SCARLATOS. 1985. "Breach erosion of earthfill dams and flood routing", BEED Model, Research Report, Army Research Office, Battelle, Research Triangle Park, NC, US, 131 p.

17. SINGH, V. P. 1996. "Dam breach modelling technology", Kluwer Publisher, Dordrecht, The Netherlands.

18. SOIL CONSERVATION SERVICE. 1981. "Simplified dam breach routing procedure", December, Technical Release No 66 (Rev. I), 39p.

19. WADLER, J. S. y J. E. O'CONNOR. 1997. "Methods for predicting peak discharge of floods caused by failure of natural and constructed earth dams", October, Water Resources Research, 33(10), 12p.

20. WAHL, T. L. 1998. "Prediction of embankment dam breach parameters", DSO-98-004, Dam Safety Research Report, US Department of the Interior, Bureau of Reclamation, Dam Safety Office.