♦ Iniciación del movimiento ♦

La iniciación del movimiento es el umbral en el que las partículas de sedimento comienzan a moverse en un flujo en canal abierto. Este umbral es importante en el diseño de canales para asegurar el movimiento de sedimentos y evitar obstrucciones. El número de Froude F = 0,08 a menudo se ha tomado como valor mínimo para evitar obstrucciones. Aquí derivamos un criterio general de Froude para la iniciación del movimiento, lo que confirma la validez de F = 0,08 en una amplia gama de aplicaciones prácticas.

♦ Criterio de Shields ♦

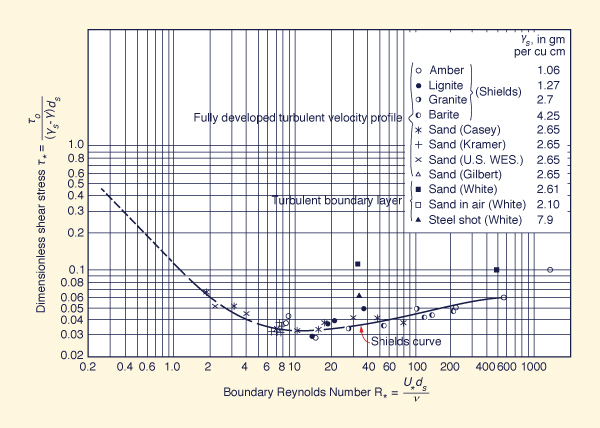
El criterio de Shields para la iniciación del movimiento relaciona el esfuerzo cortante adimensional τ_* con el número de Reynolds límite R_*, como se muestra en la figura anterior.¹ La curva continua separa el movimiento por encima de la curva, de la ausencia de movimiento por debajo de la curva. El criterio de Shields es el siguiente:

τo τ* = ____________  ≥  τ*c           (γs - γ) ds

(1)

en la cual τ_o = esfuerzo cortante en el fondo, γ_s = peso específico de las partículas de sedimento, γ = peso específico del agua, d_s = diámetro de las partículas del sedimento, y τ_*c = esfuerzo cortante crítico adimensional.

Para aplicaciones prácticas, el esfuerzo cortante crítico adimensional τ_*c puede tomarse como una constante para una amplia gama de números de Reynolds limite R_*.

♦ Fricción cuadrática ♦

La fórmula de fricción cuadrática es: ²

τo = ρ f v 2

(2)

en la cual ρ = densidad de masa del agua, f = factor de fricción, igual a 1/8 del factor de fricción de Darcy-Weisbach f_D, y v = velocidad media.

♦ Criterio de Froude ♦

El número de Froude es:

v F = _________          (gd)1/2

(3)

en la cual g = aceleración gravitacional, y d = profundidad del flujo (sección transversal hidráulicamente ancha).

♦ Criterio de Froude para la iniciación del movimiento ♦

Reemplazando las Ecs. 2 y 3 en la Ec. 1:

f d F2 ___________________  ≥  τ*c       [ (γs/γ) - 1 ] ds

(4)

En la mayoría de los casos, la relación γ_s/γ = 2.65. Por lo tanto, el criterio de Froude se reduce a:

1.65 τ*c (ds / d) F  ≥  { __________________ }1/2                           f

(5)

Como una aproximación conveniente, la curva de Shields sugiere un valor de esfuerzo cortante adimensional crítico τ_*c = 0.04 para una amplia gama de números de Reynolds de límite. Por lo tanto:

0.066 (ds / d) F  ≥  { ________________ }1/2                       f

(6)

El factor de fricción varía normalmente en el rango 0,002 ≤ f ≤ 0,005, que corresponde al factor de fricción de Darcy-Weisbach 0,016 ≤ f_D ≤ 0.040. Asumimos un valor medio de f = 0.0035, correspondiente a f_D = 0.028. El criterio de Froude se reduce a:

F  ≥  [ 18.86 (ds / d) ]1/2

(7)

que se reduce a:

F  ≥  4.342 (ds / d)1/2

(8)

Para un diámetro de partícula dado, en relación con la profundidad del flujo, la Ec. 8 establece el número de Froude que debe superarse para asegurar el inicio del movimiento. Por ejemplo, para d_s / d = 0.0004, es decir, un tamaño de partícula de 0,4 mm en 1 m de profundidad, la Ec. 8 se reduce a:

F  ≥  0.087

(9)

Para d_s / d = 0.0003, la Ec. 8 se reduce a:

F  ≥  0.075

(10)

♦ Ejemplo ♦

Supongamos: (a) un factor de fricción f = 0,005 (un valor alto), y (b) un diámetro de partícula relativo d_s / d = 0.0005 (un valor alto). La aplicación de la Ec. 6 resulta en:

F  ≥  0.081

(11)

♦ Aplicación con n de Manning ♦

La relación entre el factor de fricción f y la n de Manning es:

g n2 f = ___________          k2 R1/3

(12)

en la cual g = aceleración gravitacional, n = n de Manning, R = radio hidráulico, y k = una constante igual a 1 en unidades SI, y 1,486 en unidades habituales de EE.UU.

Para un canal hidráulicamente ancho: R ≅ d. Reemplazando la Ecuación 12 en la Ecuación 6, la expresión del número de Froude en unidades SI es la siguiente:

0.082 d1/6 (ds / d)1/2 F  ≥  _______________________                         n

(13)

Por ejemplo, para d = 1 m, d_s = 0.4 mm = 0.0004 m, y n = 0.020:

F  ≥  0.082

(14)

En las unidades habituales de EE. UU., la expresión del número de Froude es la siguiente:

0.067 d1/6 (ds / d)1/2 F  ≥  _______________________                          n

(15)

en la cual d y d_s se expresan en pies.

Por ejemplo, para d = 1 m = 3.28 pies, d_s = 0.4 mm = 0.0004 m = 0.001312 pies, y n = 0.020:

F  ≥  0.082

(16)

♦ Resumen ♦

El criterio de Shields se expresa en términos del número de Froude, lo que permite el cálculo del número de Froude mínimo para el inicio del movimiento [sedimento del material del lecho] en el flujo en canales abiertos. Dado el esfuerzo cortante adimensional crítico, el factor de fricción y el diámetro relativo de las partículas, la relación desarrollada confirma la validez del número de Froude F = 0.08 como un descriptor apropiado del inicio del movimiento en la mayoría de los casos de interés práctico.