In September of 1976, I began work on a two-dimensional model of water and sediment routing, under the direction of Dr. Daryl B. Simons, who at the time was associate dean for research at the College of Engineering, Colorado State University, Fort Collins, Colorado. After a few months of painstaking model development, Dr. Simons had a chance to review our progress. The task at hand was to model the flow of a river, in and out of a side embayment. 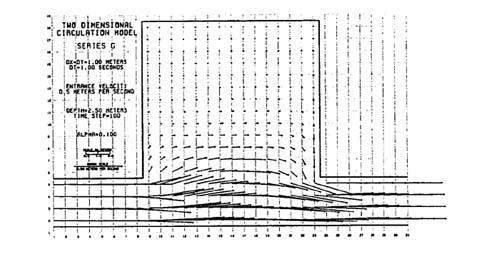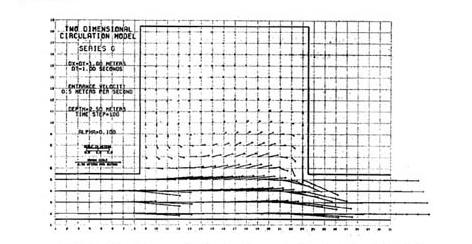Our results showed that the flow appeared to convect properly, as shown in Fig. 1 (a); however, Dr. Simons was not convinced. In his experience, the flow pattern was not supposed to be clockwise, but rather counterclockwise. We went back to the drawing board, eventually obtaining funds from the National Science Foundation to study two-dimensional flow circulation.

Our subsequent research provided an answer to the puzzle.¹ Whether the two-dimensional flow in an embayment was clockwise, as our model originally indicated (Fig. 1 a), or counterclockwise, to agree with Simons' experience (Fig. 1 b), depended on the problem scale. Under large scale, friction dominated and the resulting flow was clockwise; conversely, under small scale, inertia dominated and the resulting flow was counterclockwise. Thus, the model was correct; the problem was convective for large scale and diffusive for small scale. Surprisingly, this finding extended to two-dimensional flow our earlier finding regarding the role of scale in one-dimensional wave propagation.²

¹ Ponce, V. M., and S. B. Yabusaki. 1981. Modeling circulation in depth-averaged flow. Journal of the Hydraulics Division, ASCE, Vol. 107, HY11, November, 1501-1518.

² Ponce, V, M., and D. B. Simons. 1977. Shallow wave propagation in open-channel flow. ASCE Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, December, 1461-1476.