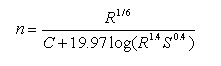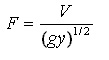|
|
|
| 1. Introduction |
|
A gabion system is wire-enclosed riprap consisting of mats or baskets fabricated with wire mesh, filled with small
riprap, and anchored to a slope (Fig. 1). Wrapping the
riprap enables the use of smaller stone sizes for the same resistance to displacement by water energy. This is a particular advantage
when constructing rock lining in areas of difficult access. The wire basket also allows steeper (up to vertical) channel linings
to be constructed from commercially available wire units or from wire-fencing material.
Due to their high shear strength, gabion systems provide a highly effective way to control erosion in streams, rivers and canals. They are normally designed to sustain channel velocities of 15 fps or higher. Gabions are constructed by individual units that vary in length from 6 ft to nearly 100 ft (gabion mats); therefore, applications can range anywhere from small ditches to large canals. Gabion channels are a compromise between riprap and concrete channels. When the same-size rocks are used in gabions and riprap, the acceptable velocity for gabions is at least 3-4 times that of riprap. Unlike concrete, gabions can be vegetated to blend into the natural landscape (Fig. 2). Gabion channels with vegetation have the following advantages:
|
| 2. Manning's n |
|
The Manning's n or roughness coefficient for gabion channels with vegetation depends primarily on the type of
vegetation and the size of the stones being used.
There is no specific formula for the roughness coefficient for gabion channels with vegetation. The roughness coefficient can be derived by knowing other values
of Manning's n
and relating them to the specific case. For gabions without vegetation, Manning's n ranges from 0.025 to 0.03. Manning's n for vegetated channels also vary
depending
on the type of soil, the amount of cover, resistance and retardance. Manning's n for vegetative channels is given by the following formula:
There is no specific formula for Manning's n for channels with concrete, gabion or riprap lining. Table 2 shows frequently used Manning's n.
Riprap channels have a very large range of Manning's n, depending on the stone diameter and the flow depth.
The Manning's n of the composite channel is given by the following formula:
In gabion channels with vegetation (Fig. 5), the value of Manning's n is estimated by experience.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 3. Gabion facts |
|
The procedure for placing and filling gabions can be summarized as follows: (1) Assembling the individual units before placing
(Fig. 6); (2)
placing them and wiring them together and filling the units with rocks (Fig. 7); and (3) closing and wiring down the lids
(Fig. 8). Gabions can be placed on
dry bank (Fig. 9) or under water (Fig. 10). Linings laid in dry conditions are placed directly on a stable slope which is not too steep as to cause the revetment to slide. The units are normally laid down on the slope of the bank, at right angles to the current. However, the units on the bed itself should be laid in the direction of flow. When constructing a lining under water, dumping riprap is challenged by the many uncertainties, since it is difficult to obtain a uniform distribution of the material over the whole area to be protected. In order to reduce the risk, the amount of rocks dumped has to be increased by 50%. This problem does not arise with gabions, since the structure is preassembled and of fixed thickness. The gabions can are placed using cranes or pontoons (Fig. 11). The stability of gabion linings depends on the strength of the mesh, the thickness of the lining and the grading of the stone fill. Once the water velocity is known, these parameters can be selected. For longevity of the revetment, the mesh must be protected from corrosion. Gabions are constructed from wires with heavy zinc content and PVC coating. |
| 4. Design criteria |
|
The two primary elements in channel design are cross-sectional shape and lining (Fig. 12).
Lining is determined by erosion resistance and drainage requirements. Vegetated linings are appropiate for low velocities. Paved linings may be used for soil-water
interfaces where the soil and groundwater conditions are such that the soil may erode under the design flow. Generally, velocities over 5 fps
will require lined waterways.
For design purposes, uniform flow conditions are usually assumed, with energy slope (Sf) equal to average bed slope (So).
This allows the flow conditions to be defined by a uniform flow equation such as Manning's. Supercritical flow creates surface waves of depth comparable to the
flow depth. For very steep channel gradients, the flow may splash and surge; therefore special considerations for freeboard are required.
Once the basic hydraulic and physical characteristics of the channel have been determined,
the selection of the lining and stability analysis can be made. Generally, a 10-yr to a 100-yr storm is used to determine capacity, while the 2-yr
storm is used to channel stability. After vegetation is fully developed, the channel is considered stable and capacity become more critical.
Channels should be designed so that the flow velocity does not exceed the permissible velocity for the type of lining used.
It is also important to check outlets for stability. Excessive velocities or grade changes may require protective or stabilizing structures, transition sections, or energy
dissipators to prevent erosion or scour.
Gabion thickness depends on manufacturer specifications and stone sizes, which may range from 4 to 8 in. Gabion systems are subject to clogging by sediment. The Froude
number is defined as follows:
|
| 5. Summary |
|
|
http://ponce.sdsu.edu/manningsn_hydroecological.html
|
081013
|