1.  MODELO DE PENMAN

El modelo original de Penman es un método de combinación en el que la tasa de evaporación total se calcula combinando la tasa de evaporación debida a la radiación neta y la tasa de evaporación debida a la transferencia de masa, de la siguiente manera (Ponce, 1989):

en la cual E = tasa de evaporación total; E_n = tasa de evaporación debido a radiación neta; E_a = tasa de evaporación debido a transferencia de masa; Δ = gradiente de la presión de vapor de saturación, una función de la temperatura del aire; y γ = constante psicrométrica, la cual varía ligeramente con la temperatura. La tasa de evaporación de transferencia de masa E_a se calcula utilizando una fórmula empírica.

2.  MODELO DE PENMAN-MONTEITH

En el método de Penman-Monteith, la tasa de evaporación de transferencia de masa E_a se calcula en base a principios físicos. La forma original de la ecuación de Penman-Monteith, en unidades dimensionalmente consistentes, es la siguiente:

en la cual:

• ρλE = flujo total de energía evaporativa, en cal/(cm²-s);

• ρ = densidad del agua, en gr/cm³;

• λ = calor de vaporización, en cal/gr;

• E = tasa de evaporación, en cm/s;

• Δ = gradiente de presión de vapor de saturación, en mb/°C;

• H = flujo de energía suministrado externamente, por radiación neta, en cal/(cm²-s);

• ρ_a = densidad del aire húmedo, en gr/cm³;

• c_p = calor específico del aire húmedo, en cal/(gr-°C);

• (e_s  -  e_a) = déficit de presión de vapor, en mb;

• r_a = resistencia externa (aerodinámica), en s/cm; y

• γ * = constante psicrométrica modificada, en mb/°C, definida como sigue:

  rs γ *  =   γ   ( 1  +  _____ )                              ra

  (3)

  en la cual:

• γ = constante psicrométrica, en mb/°C, la cual varía ligeramente con la temperatura, y

• r_s = resistencia interna (estomatal o superficial), en s/cm.

La cantidad r_a^-1 es la conductancia externa, en cm³ de aire por cm² de superficie por segundo (cm/s).

En unidades de tasa de evaporación, la Ecuación 2 se expresa de la siguiente manera:

en la cual:

• E = tasa de evaporación total, en cm/s;

• E_n = tasa de evaporación debido a radiación neta, en cm/s;

• ρ = densidad del agua, en gr/cm³;

• λ = calor de vaporización, cal/gr;

  y

• Δ, γ *, ρ_a, c_p, (e_s  -  e_a), y r_a  están en las mismas unidades que en la Ecuación 2.

La Ecuación 4 es el modelo de evaporación de Penman-Monteith.

3.   CONSTANTES FÍSICAS

La densidad del aire seco a 0°C, con la presión atmosférica a nivel del mar es: ρ_ad = 1.2929 kg/m³. La densidad del aire húmedo ρ_a se puede aproximar de la siguiente manera:

en la cual T = temperatura del aire, en °C.

Por ejemplo, a T = 20°C y nivel del mar (presión atmosférica estándar):

ρ_a = 0.0012046 gr/cm³.

El calor específico del aire húmedo, en el rango 0°C ≤ T ≤ 40°C, es:

c_p = 1.005 J/(gr-°C)

Convirtiendo a calorías:

c_p = (1.005 J/(gr-°C) (0.239 cal/J) = 0.2402 cal/(gr-°C).

4.  TASA DE EVAPORACIÓN DIARIA

En unidades de evaporación de cm/d, la Ecuación 4 se expresa de la siguiente manera:

en la cual:

• E = tasa de evaporación total (cm/d);

• E_n = tasa de evaporación debido a radiación neta (cm/d); y

• Δ, γ *, ρ_a, c_p, (e_s  -  e_a), r_a, ρ, y λ están en las mismas unidades que en las Ecs. 2 y 4.

La Ecuación 6 se puede expresar convenientemente en forma de Penman (Ec. 1) de la siguiente manera:

en la cual E_a = tasa de evaporación debido a transferencia de masa, en cm/d.

5.  TASA DE EVAPORACIÓN POR TRANSFERENCIA DE MASA

Comparando las Ecs. 6 y 7 se obtiene la tasa de evaporación por transferencia de masa:

Simplificando la Ec. 8:

en la cual K = constante que varía con la temperatura del aire y la presión atmosférica, en unidades de s/(d-mb), expresada como sigue:

En la Ecuación 10, las unidades de ρ_a, c_p, ρ, λ, y γ son las mismas que en las Ecs. 2 y 4.

La constante psicrométrica γ, en mb/°C, es la siguiente:

en la cual c_p = calor específico del aire húmedo, en cal/(gr-°C); p = presión atmosférica, en mb; λ = calor de vaporización, en cal/gr; y r_MW = relación entre el peso molecular del vapor de agua y el aire seco: r_MW = 0.622.

Sustituyendo la Ecuación 11 en la Ecuación 10:

en la cual la constante K permanece en unidades s/(d-mb).

Reemplazando r_MW = 0.622 en la Ec. 12:

en la cual la constante K permanece en unidades de s/(d-mb).

Para T = 20°C y presión atmosférica estándar (nivel del mar): ρ_a = 0.0012046 gr/cm³, ρ = 0.99821 gr/cm³, y p = 1013.25 mb. Por lo tanto, la constante K en la Ec. 13 se reduce a: K = 0.064 s/(d-mb), y la Ec. 9 se reduce a lo siguiente:

en la cual:

• E_a = tasa de evaporación debido a transferencia de masa, en cm/d;

• (e_s  -  e_a) = déficit de presión de vapor, en mb;

• r_a = resistencia externa (aerodinámica), en s/cm; y

• r_s = resistencia interna (estomática), en s/cm.

6.  RESISTENCIA EXTERNA

La resistencia externa o aerodinámica r_a varía con la rugosidad de la superficie (agua, suelo o vegetación), siendo inversamente proporcional a la velocidad del viento (Ec. 15). En otras palabras, la conductancia externa y, por lo tanto, la tasa de evaporación, aumenta con la velocidad del viento, como fue postulado originalmente por Dalton (Ponce, 1989).

La resistencia externa para la evaporación de una superficie de agua se puede estimar de la siguiente manera:

en la cual:

• r_a = resistencia externa, en s/m;

• z_m = altura a la que se miden las variables meteorológicas, en m;

• z_o = rugosidad aerodinámica de la superficie, en m; y

• v₂ = velocidad del viento, en m/s, medida a 2 m de altura.

La resistencia externa r_a (s/m) para el cultivo de referencia (hierba recortada de 0,12 m de altura), para mediciones de velocidad del viento (m/s), temperatura y humedad a una altura estandarizada de 2 m es la siguiente:

Por ejemplo, para v₂ = 200 km/d = (200000 m) / (86400 s) = 2.31 m/s, la resistencia externa o aerodinámica del cultivo de referencia es la siguiente:

7.  RESISTENCIA INTERNA

La resistencia interna, estomática o superficial r_s es inversamente proporcional al índice de área foliar L. Una relación empírica para la resistencia superficial (interna) es (Maidment, 1993):

en la cual r_s   está expresado en unidades s/m.

El índice de área foliar L está empíricamente relacionado con la altura del cultivo h_c. El índice de área foliar para césped recortado es el siguiente:

en la cual h_c = altura del cultivo, en m, la cual varía en el rango 0.05 ≤ h_c ≤ 0.15.

De las Ecs. 18 y 19, la resistencia superficial del cultivo de referencia (hierba recortada de 0,12 m de altura) es: r_s^rc = 200 / (24 × 0.12) = 69.4 s/m.

El índice de área foliar de la alfalfa es el siguiente:

en la cual la altura del cultivo h_c está en metros, variando en el rango 0.1 ≤ h_c ≤ 0.5.

De la Ecuación 20, para h_c = 0.3 m, el índice de área foliar de alfalfa es: L = 3.69. De la Ecuación 18, la resistencia superficial de la alfalfa es: r_s = 200 / 3.69 = 54.2 s/m.

8. EJEMPLO ILUSTRATIVO

Calcular la tasa de evaporación del cultivo de referencia (pasto cortado) por el método de Penman-Monteith para el mes de abril, para las siguientes condiciones atmosféricas: temperatura del aire T_a = 20°C; radiación neta Q_n = 550 cal/(cm²-d); velocidad del viento v₂ = 200 km/d; y humedad relativa φ = 70%. Suponer una presión atmosférica estándar.

Solución.

• El gradiente de presión de vapor de saturación es (Ponce, 2014: Section 2.2):

  Δ = (0.00815 T_a  +  0.8912)⁷ = 1.447 mb/°C.

• La radiación neta en unidades de tasa de evaporación es (Ponce, 2014: Section 2.2):

  E_n = Q_n / ( ρ λ ) = 550 / (0.99821 × 586) = 0.94 cm/d

• Utilizando la Ec. 16, la resistencia externa del cultivo de referencia es el siguiente:

  r_a^rc = (208 × 86400) / (200 × 1000) = 90 s/m = 0.9 s/cm

• La resistencia interna del cultivo de referencia es:

  r_s^rc = 200 / (24 x 0.12) = 69.4 s/m = 0.694 s/cm

• La constante psicrométrica, Ec. 11, es la siguiente:

  γ = (0.2402 × 1013.25 ) / (586 × 0.622) = 0.668

• La constante psicrométrica modificada, Ec. 3, es el siguiente:

  γ * = 0.668 [ 1 + (0.694 / 0.9 ) ] = 1.18

• El déficit de presión de vapor es (Ponce, 2014: Sección 2.2):

  (e_s - e_a) ≅ (e_o - e_a) = e_o [ 1 - (φ / 100) ] = 23.37 [ 1 - (70 / 100)] = 7.01 mb.

• La tasa de evaporación por transferencia de masa, Ec. 14, es el siguiente:

  E_a = ( 0.064 × 7.01 ) / ( 0.9 + 0.694 ) = 0.2815 cm/d.

• La tasa de evaporación total, Ec. 7, es la siguiente:

  E = [ ( 1.447 × 0.94 ) + ( 1.18 × 0.2815 ) ]  /  ( 1.447 + 1.18 ) = 0.644 cm/d.

• La tasa de evaporación para el mes de abril es: E = 30 × 0.644 = 19.32 cm.

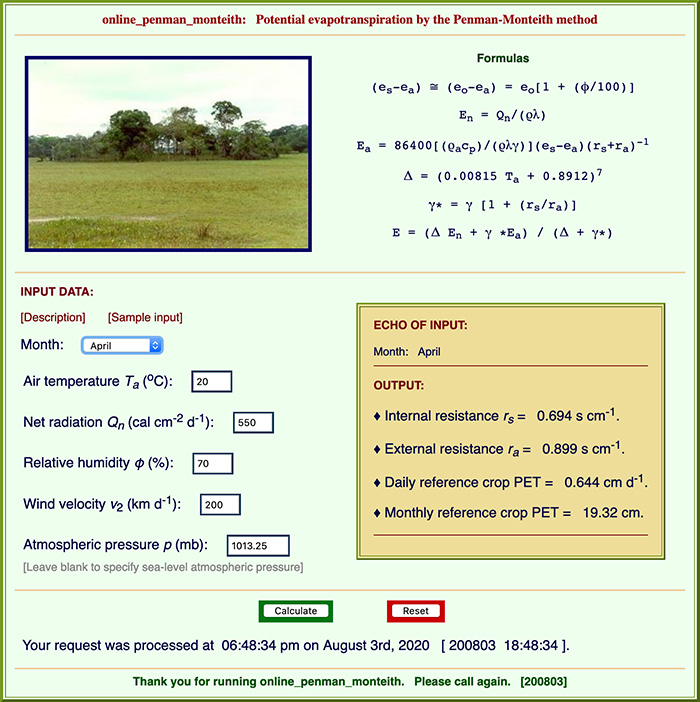
CÁLCULO EN LÍNEA. Utilizando ENLINEAPENMANMONTEITH, la respuesta es: Cultivo diario de referencia PET = 0.644 cm/d; cultivo de referencia mensual PET (Abril) = 19.32 cm. Estos resultados son los mismos que el cálculo manual que se muestra arriba.

BIBLIOGRAFÍA

Maidment, D. R. 1993. Handbook of Hydrology. McGraw-Hill.

Ponce, V. M. 1989. Engineering Hydrology: Principles and Practices. Prentice Hall, Englewood Cliffs, New Jersey.

Ponce, V. M. 2014. Engineering Hydrology: Principles and Practices. Online text.