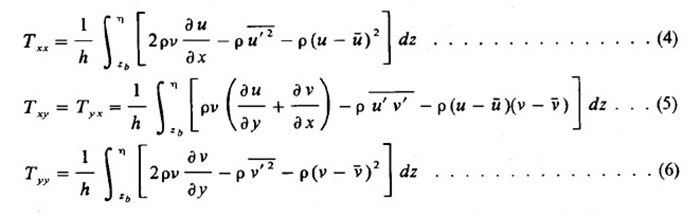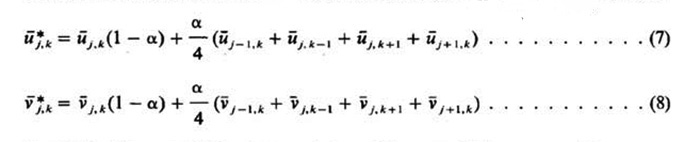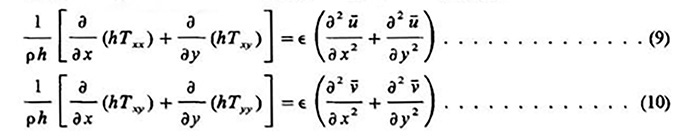1.  INTRODUCCIÓN

Existe una clase de problemas de flujo en canal abierto que pueden describirse adecuadamente en el contexto de modelos matemáticos de dos dimensiones, promediados en la profundidad. Esencialmente, estos modelos son capaces de resolver corrientes de flujo en dos direcciones horizontales, asumiendo que las propiedades del fluido y del flujo no varían a lo largo de la vertical. Tales representaciones simplificadas de un fenómeno tridimensional se justifican cuando la mezcla turbulenta, debido a la rugosidad de fondo, genera efectivamente una distribución uniforme de la velocidad a través de la profundidad de flujo.

Los efluentes térmicos de las instalaciones de enfriamiento, las descargas de contaminantes de las plantas de procesamiento químico, y el movimiento de sedimentos por erosión local son evidencia de una industrialización progresiva que tiene el potencial de afectar la acción de limpieza natural de las vías fluviales hasta el punto en que pueden producirse graves consecuencias ambientales. El conocimiento del efecto de las modificaciones propuestas es vital para el desarrollo y utilización de las vías fluviales.

En este estudio, se realiza una investigación básica de los fenómenos de circulación en canales abiertos utilizando un modelo matemático de dos dimensiones, promediado en la profundidad. Se ha observado que la circulación tiene una influencia principal en los procesos de erosión y sedimentación, difusión de calor y dispersión de contaminantes. Por lo tanto, la aclaración de los mecanismos físicos que conducen a la generación de circulación en el flujo bidimensional de superficie libre es un tema importante de investigación.

2.  REVISIÓN DE LA LITERATURA

Previo al desarrollo de la computación eficiente, el investigador interesado en modelar el flujo de superficie libre disponía de dos alternativas: (1) soluciones analíticas; y (2) modelos físicos. A pesar de proporcionar los resultados más precisos, las soluciones analíticas son extremadamente raras y se aplican sólo en situaciones muy simplificadas. Por el contrario, los modelos físicos se utilizan ampliamente y con bastante éxito. La mayoría de los inconvenientes asociados con los modelos físicos son de carácter económico debido al elevado costo de construcción y al tiempo necesario para simular adecuadamente las condiciones del prototipo. Sin embargo, la falta de flexibilidad es probablemente el mayor impedimento para seleccionar un modelo físico, ya que un cambio en la configuración generalmente implica costosas modificaciones.

La mayor eficiencia de las computadoras ha llevado a un gran esfuerzo de investigación en el refinamiento de los modelos matemáticos. Si bien ofrecen una flexibilidad casi ilimitada en la simulación de alternativas, estos modelos tienen el atractivo adicional de tener menores costos de desarrollo y operativos. Algunos problemas especializados aún permanecen dentro del ámbito del modelo físico, pero el uso de modelos matemáticos continúa aumentando.

Los modelos matemáticos de flujo en canal abierto existen en varios niveles de complejidad. La descripción detallada de los fenómenos de flujo se logra mejor en un marco espacial tridimensional; sin embargo, la complejidad de una formulación en tres dimensiones a menudo requiere enormes cantidades de recursos computacionales. Cuando válida, la simplificación a una representación bidimensional puede ofrecer una reducción considerable en complejidad. Esto implica una integración de las ecuaciones tridimensionales de la dinámica de fluidos a través de la profundidad del flujo. El sistema bidimensional de ecuaciones integradas en la profundidad no está exento de dificultades: existe un problema de cierre asociado con los esfuerzos cortantes efectivos que actúan tangencialmente en los lados verticales de un elemento de fluido. Actualmente no se dispone de una relación rigurosa entre estas tensiones y las variables promediadas en profundidad.

A Hansen (6) se le atribuye el mérito de ser el primero en delinear la formulación bidimensional promediada en profundidad. Posteriormente, otros investigadores, sobre todo Leendertse (10, 11), siguieron a Hansen en la aplicación de conceptos de modelado bidimensional al estudio de la hidrodinámica costera y estuarina. En un análisis detallado del flujo de superficie libre, Leendertse desarrolló un modelo computacional para la propagación de ondas de largo período en estuarios bien mezclados y mares costeros (10). En el trabajo de Leendertse se hizo especial hincapié en las propiedades numéricas del modelo bidimensional en forma de análisis lineal de estabilidad y convergencia siguiendo el enfoque de von Neumann.

Kuipers y Vreugdenhil (7) ampliaron el modelo de 1967 de Leendertse al ámbito de los flujos secundarios. Al imponer una condición de flujo permanente en las fronteras, pudieron utilizar el carácter no permanente del modelo de Leendertse como una técnica iterativa para acercarse al flujo permanente de circulación bajo condiciones de frontera específicas. Se realizó un análisis teórico de los mecanismos de generación de vorticidad para arrojar luz adicional sobre las causas del flujo de circulación en modelos bidimensionales promediados en profundidad. De acuerdo con Kuipers y Vreugdenhil, si se ignoran la carga de viento, la vorticidad puede ser creada por los términos convectivos que interactúan con el flujo convergente o divergente o por los esfuerzos cortantes efectivos. Los experimentos numéricos mostraron la necesidad de incluir los términos de inercia convectiva para modelar el flujo circulante bidimensional. La circulación observada en el modelo se atribuye al efecto combinado de los términos de inercia convectiva y la viscosidad artificial, ya que no se consideró explícitamente los esfuerzos efectivos.

En un informe que acompaña al de Kuipers y Vreugdenhil, Flokstra (3) ha dirigido la atención a la importancia de modelar correctamente los esfuerzos cortantes efectivos. Sin resolver el problema de cierre asociado con el modelado de estos esfuerzos, Flokstra realizó un análisis detallado de los mecanismos físicos que contribuyen a la generación de circulación. De acuerdo con el balance de vorticidad de Flokstra, es teóricamente imposible generar flujo circulante sin modelar el esfuerzo cortante efectivo. Además, el análisis de Flokstra llevó a la conclusión de que la condición de velocidad nula en las paredes es esencial para la generación de flujo de circulación.

Abbott y Rasmussen (1) verificaron la conclusión de Kuipers y Vreugdenhil de que los términos de inercia convectiva son necesarios para la generación de circulación. Utilizando un razonamiento físico, atribuyeron los patrones de circulación a la dominación de los efectos de resistencia de fondo sobre los efectos de inercia. Abbott y Rasmussen también concluyeron que las "pseudocirculaciones", que se producen estrictamente debido a los errores de truncamiento de los esquemas de diferencias de primer orden, eran posibles en modelos bidimensionales promediados en profundidad.

Flokstra (4) también estudió la ocurrencia de inestabilidad no lineal en modelos numéricos bidimensionales. Se citaron tres enfoques para resolver este problema: (1) Un proceso de suavizado espacial similar al utilizado por Kuipers y Vreugdenhil; (2) la introducción explícita de un término de viscosidad artificial en las ecuaciones de movimiento; y (3) el uso de un esquema de diferencias finitas afectado por la viscosidad numérica.

McGuirk y Rodi (12) desarrollaron un modelo de velocidad promediada en profundidad y distribución de contaminantes, que describía la región de recirculación inmediatamente aguas abajo de una descarga lateral en un río. Considerando el constante coeficiente de difusión turbulenta y las representaciones no explícitas de la estructura turbulenta demasiado gruesas para los fenómenos de chorro lateral, McGuirk y Rodi utilizaron una extensión del modelo de turbulencia bidimensional de Launder y Spalding (8).

Lean y Weare (9) probaron las conclusiones teóricas de Flokstra utilizando un modelo de circulación promediado en profundidad de los flujos más allá de un rompeolas. Se demostró que los esfuerzos efectivos tienen contribuciones de la turbulencia de la capa de cizallamiento y la turbulencia generada en el lecho. Se presentan criterios para delimitar las condiciones bajo las cuales predominará la turbulencia de la capa de cizallamiento. Se reporta una observación de circulación numérica (5) similar a la experimentada por Abbott y Rasmussen pero causada por una malla computacional gruesa.

En la actualidad, existen varias incertidumbres en el modelado matemático del flujo bidimensional en canal abierto, promediado en profundidad. En la literatura se encuentran varios modelos que exhiben circulación, y numerosas estudios sobre los factores causantes de esta circulación. Sin embargo, aún no se ha intentado un análisis exhaustivo de los diversos mecanismos que conducen a la circulación en conjunción con un modelo numérico. Los objetivos de este estudio son, por lo tanto: (1) el esclarecimiento de los procesos físicos que contribuyen a la generación de circulación; y (2) la identificación de factores importantes en la especificación numérica de problemas de flujo de circulación.

3.  ECUACIONES DE GOBIERNO

La derivación de las ecuaciones que gobiernan el flujo en superficie libre promediado en profundidad se logra mediante la simplificación sucesiva de las ecuaciones generales del flujo en tres dimesiones, es decir, las ecuaciones de Navier-Stokes. Cuatro supuestos son básicos para el conjunto de ecuaciones utilizado en este estudio: (1) el agua es incompresible; (2) las velocidades y aceleraciones verticales son despreciables; (3) los esfuerzos de viento y los efectos geostróficos son insignificantes; y (4) los valores promedio son suficientes para describir las propiedades que varían a lo largo de la profundidad del flujo.

Los efectos de la densidad del fluido no se consideran en este estudio; por lo tanto, la incompresibilidad es una limitación para la aplicabilidad del modelo. El segundo supuesto es una consecuencia de la magnitud relativamente grande de la fuerza del cuerpo gravitacional que, en flujos de poca profundidad, simplifica la componente-z de la ecuación de movimiento a una distribución de presión hidrostática en la vertical. Para el tipo de flujo en consideración, es decir, flujo en canal abierto, la magnitud del viento y los efectos geostróficos son insignificantes en comparación con las fuerzas impulsoras encontradas en las corrientes. Estos dos términos pueden incorporarse posteriormente al modelo, y su ausencia no resta valor a la generalidad de las conclusiones de este estudio. La suposición más importante es que un valor medio es capaz de representar una propiedad que normalmente varía a lo largo de la profundidad de flujo. Hasta que se hace esta suposición, el análisis es fundamentalmente tridimensional. Debido al promediado de la profundidad, la información sobre la distribución vertical de la velocidad se pierde parcialmente. Sin embargo, las aguas poco profundas que se encuentran en ríos y estuarios bien mezclados generalmente no requieren información muy detallada.

Las ecuaciones resultantes promediadas en la profundidad son:

en la cual ū, v̄ = velocidades promediadas en la profundidad; t = tiempo; x, y = direcciones de las coordenadas; g = aceleración de la gravedad; η = elevación del agua (η = h + z_b); ρ = densidad del fluido; τ_bx, τ_by = esfuerzos cortantes de fondo, y T_xx, T_xy, y T_yy = esfuerzos cortantes efectivos definidos como sigue:

en la cual ν = viscosidad cinemática; y u' y v' = fluctuaciones turbulentas de velocidad.

El conjunto de ecuaciones citado, aunque contiene varias aproximaciones, no está cerrado. Históricamente, la teoría del flujo turbulento ha sufrido una representación física incompleta de la transferencia de momento turbulento (tensiones de Reynolds), es decir, aquellas tensiones debidas a las correlaciones de fluctuaciones turbulentas de velocidad. Promediar la profundidad de la formulación complica aún más el problema al crear una tensión adicional debido a la distribución de velocidad no uniforme en la vertical. Estos dos esfuerzos y el esfuerzo cortante viscoso se combinan en los términos previamente identificados como el esfuerzo cortante efectivo.

El representar los esfuerzos cortantes efectivos en términos de las variables de flujo promedio es el mayor impedimento para el modelado adecuado del flujo de circulación usando profundidad promediada. Dado que este problema queda aún por resolver, se indica el uso de parámetros empíricos y técnicas de calibración. En este estudio se adopta el procedimiento desarrollado por Kuipers y Vreugdenhil (7). Esta técnica en particular no incluye explícitamente los esfuerzos cortantes efectivos en el conjunto de ecuaciones, pero los introduce en un proceso de promedio de velocidad que simula efectivamente la contribución de los esfuerzos efectivos. Este proceso consiste en un procedimiento de promediado después de que se ha generado cada conjunto de nuevas variables dependientes, de la siguiente manera:

en la cual ū_j,k* = ū_j,k promediado espacialmente; v̄_j,k* = v̄_j,k promediado espacialmente; α = factor de ponderación; y j,k = índices espaciales. Cuando se realizan estas sustituciones en las ecuaciones de gobierno, los términos de cierre aparecen de tal manera que:

en la cual ∈ = (Δx)² /(2Δt ); α = Δx = paso espacial; y Δt = paso temporal.

El esfuerzo cortante de fondo, como el esfuerzo cortante efectivo, no se ha relacionado rigurosamente con las propiedades de flujo. Sin embargo, años de experimentación han dado como resultado el desarrollo de varias ecuaciones de resistencia empíricas satisfactorias. Cualquiera de las ecuaciones de resistencia aplicables se puede utilizar para relacionar el esfuerzo cortante del fondo con la velocidad del flujo, asumiendo la validez de una rugosidad de flujo uniforme y estable. La expresión de Chexy se prefiere aquí por simplicidad, debido al factor de fricción adimensional f_r asociado con él, de la siguiente manera:

en la cual f_r = g /C ² y C = coeficiente de Chezy.

4.  MODELO MATEMÁTICO

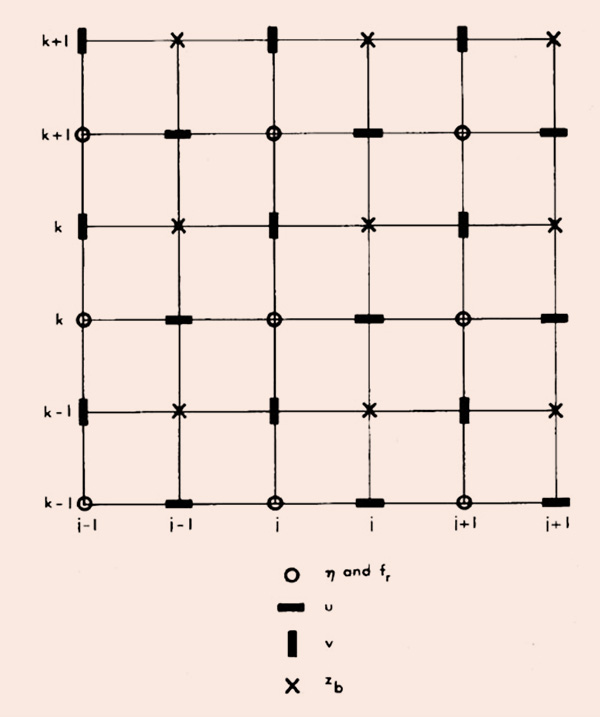
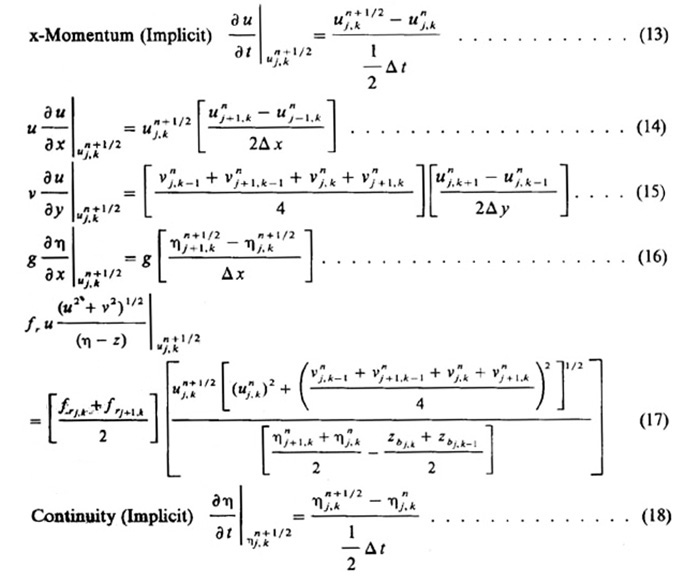
Se utiliza una aproximación en diferencias finitas para representar la ecuación diferencial parcial establecida en el modelo numérico. Para visualizar la estructura computacional, el lector debe imaginar niveles de cuadrículas horizontales x-y en capas en la dimensión vertical del tiempo. Conceptualmente, todas las cuatro variables, u, v, η, y z_b deben estar definidos en cada ubicación de nodo. Sin embargo, las limitaciones prácticas en el procedimiento computacional hacen que sea más conveniente definir un sistema de cuadrícula separado para cada una de estas variables. Estos cuatro sistemas de cuadrícula están escalonados en el espacio en una forma originalmente debida a Platzman (13), como se muestra en la Fig. 1. Normalmente, no es necesario para Δx ser igual a Δy; sin embargo, la representación de los esfuerzos cortantes efectivos usados en este modelo depende de esta suposición.

Entre los varios tipos de esquemas de diferencias finitas disponibles, las aproximaciones en diferencias centrales proporcionan precisión de segundo orden. En términos generales, las derivadas espaciales siempre se pueden expresar en un formato de diferencia central. Sin embargo, a menos que se realicen iteraciones, las derivadas temporales no se pueden representar mediante esquemas de diferencia central porque estarían de incógnitas presentes dos niveles de tiempo completo. El esfuerzo computacional adicional requerido por una formulación iterativa normalmente no está justificado. En consecuencia, se prefiere un esquema de diferencias de primer orden menos exacto pero más conveniente para las derivadas temporales.

Las ecuaciones que son no lineales con respecto a las variables desconocidas presentan grandes dificultades para una solución numérica eficiente. Aunque las ecuaciones de gobierno contienen términos no lineales, una especificación juiciosa de valores conocidos y desconocidos en las ecuaciones en diferencias finitas da como resultado una representación lineal de las variables desconocidas. Este conjunto de ecuaciones se resuelve luego mediante un eficiente algoritmo de inversión de matrices.

El procedimiento computacional utilizado en este modelo es un modo de solución multioperacional basado en la división de cada paso de tiempo Δt en dos etapas de paso de medio tiempo cada una. Leendertse (10) modificó el conocido método "implícito de dirección alterna" o IDA, al incluir dos esquemas explícitos de tal manera que cada etapa contenía un esquema implícito seguido de un esquema explícito. La ventaja del método IDA, además de las atribuibles a esquemas implícitos, radica en el procedimiento de solución que resuelve la ecuación x-momentum por separado de la ecuación y-momentum, permitiendo que el problema bidimensional se resuelva como una secuencia de dos problemas unidimensionales. Después de cada paso implícito, una sola variable dependiente permanece desconocida y puede resolverse directamente mediante un método explícito. El modelo numérico se basa en el conjunto de ecuaciones de gobierno derivado anteriormente. Cada una de las tres ecuaciones tiene un esquema de diferencias centrado en una ubicación única en la malla. La ecuación x-momentum se refiere al nodo ocupado por ū_j,k mientras que la ecuación y-momentum se centra en la ubicación del nodo v̄_j,k;η_j,k es la ubicación de referencia para la ecuación de continuidad (por simplicidad, las barras superiores se omiten a continuación).

En el modelo matemático utilizado en este estudio. los análogos en diferencias finitas de las diversas ecuaciones son, para la primera etapa:

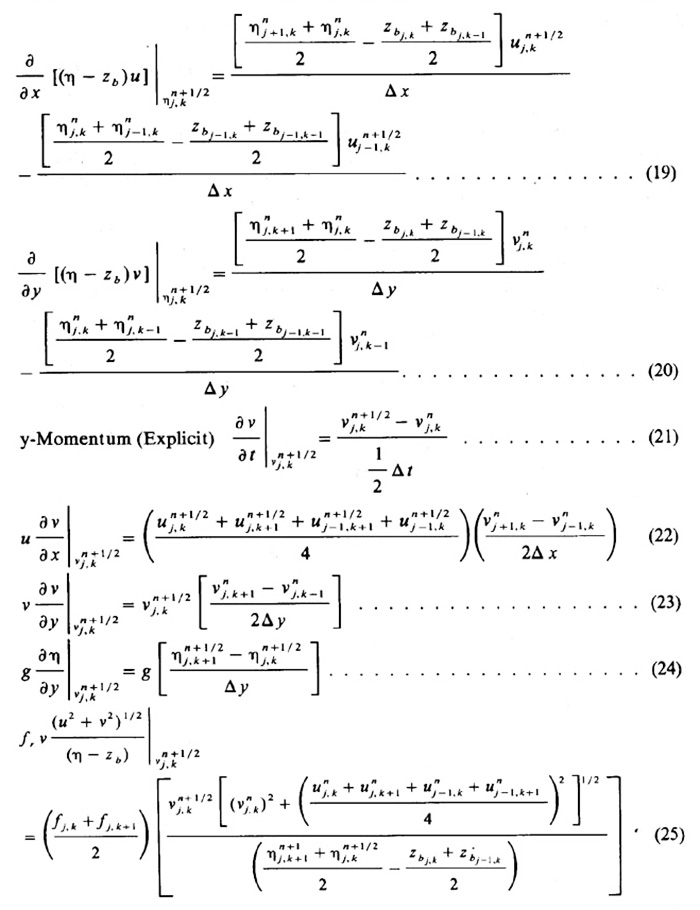
Se pueden aplicar técnicas de discretización similares para la segunda etapa: (1) y-momentum y continuidad (implícito): y (2) x-momentum (explícito). Ver Ref. 14 para obtener detalles adicionales.

Se pueden especificar dos tipos de límites en el modelo numérico: cerrados y abiertos. En límites cerrados, la especificación más conveniente es la condición de flujo de masa cero (es decir, velocidad cero) en una dirección perpendicular al límite. En los límites abiertos, se puede especificar la velocidad media o la elevación de la superficie del agua, según las necesidades del modelo.

Las diferencias finitas centrales espaciales, como las que se utilizan en este modelo, requieren información que se encuentra fuera de los límites del modelo computacional. Aunque una velocidad cero tangencial a la pared es una suposición realista (la condición de velocidad sin deslizamiento), un nivel de agua cero en el límite puede ser muy inexacto y puede dar lugar a problemas de estabilidad numérica. Una alternativa satisfactoria parece ser la reubicación de valores interiores. Se eligió una técnica de reubicación simple en la que los valores exteriores se definieron para que fueran iguales a los valores interiores adyacentes a los límites. Esto equivale a una condición de deslizamiento perfecta, una suposición razonable en flujos turbulentos en los que los efectos viscosos tienen poca influencia en la distribución de la velocidad horizontal.

Un problema generalizado en el modelado matemático bidimensional es la falta de criterios teóricos adecuados de estabilidad numérica. La teoría de la estabilidad lineal clasifica el procedimiento multi-operacional como incondicionalmente estable. Sin embargo, la experiencia (15) ha demostrado que el método es solo débilmente estable.

5.  RESULTADOS

El objetivo de la experimentación numérica es el esclarecimiento de los fenómenos de circulación existentes en el flujo en superficie libre. Se prueban dos configuraciones hipotéticas bajo una gama de condiciones iniciales y de contorno. Además de un análisis de sensibilidad, se realizan experimentos en los que se varía más de un elemento de la línea de base para determinar la interacción entre varios componentes del sistema.

La mayor parte del programa de prueba consiste en experimentos realizados en una configuración canal-área lateral. Las dimensiones del canal son de 4 m de ancho por 30 m de largo, mientras que el área lateral es un rectángulo de 14 m de ancho y 15 m de largo.

La primera serie de pruebas se realiza con una velocidad de 0.5 m/s especificada en el canal como condición inicial y en el extremo aguas arriba como condición de frontera permanente. Una profundidad de flujo de 2.5 m sirve tanto como condición inicial y como condición de frontera permanente aguas abajo. Inicialmente, no hay flujo en el área lateral. Los límites cerrados están representados por velocidades nulas en la dirección perpendicular a las paredes. Sin una pendiente del lecho, el agua en el sistema es impulsada únicamente por la velocidad de entrada aguas arriba. Los parámetros numéricos utilizados en la ejecución de la línea de base son: factor de ponderación α = 0.1, factor de fricción f_r = 0.0045, incremento espacial Δx = Δy = 1 m, e incremento temporal Δt = 1 sec. La Figura 2 es un gráfico de los vectores de velocidad de la línea de base después de 200 segundos de simulación. Aparece una circulación bien desarrollada en el área lateral con poca o ninguna divergencia del flujo principal. Los niveles de agua en el área-lateral oscilan entre 2.50 m a 2.52 m. Los niveles de entrada sin embargo, caen continuamente de 2.50 m a 2.44 m.

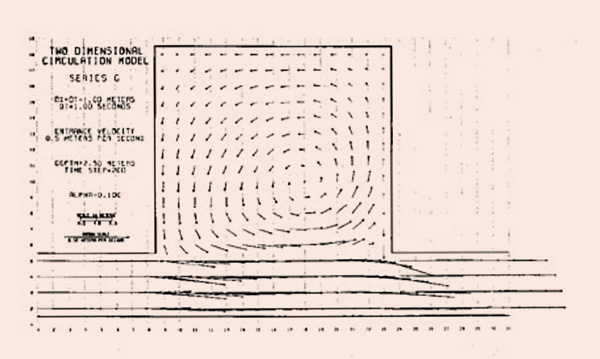
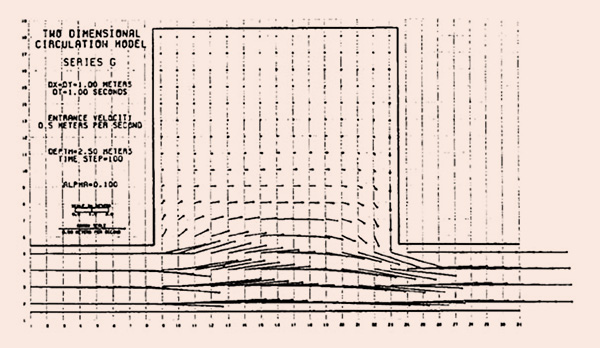
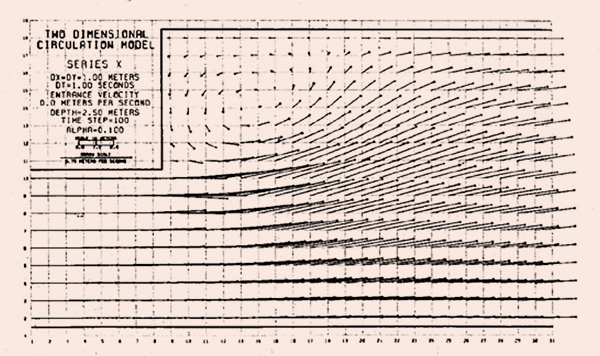
Flokstra (3) ha explicado teóricamente la necesidad de modelar los esfuerzos cortantes efectivos en los casos donde hay circulación física. En el presente modelo, la representación de los esfuerzos cortantes efectivos no es explícita en el conjunto de ecuaciones discretizadas; más bien, la acción de los esfuerzos cortantes efectivos se simula mediante una interfase que promedia la velocidad empleando un factor de ponderación α para controlar la magnitud del efecto. El primer experimento realizado en la configuración de grupo de canales omite el modelo de tensión efectiva especificando α = 0. La transferencia de impulso turbulento desde la corriente principal hacia el área lateral es insignificante en este caso. Sin divergencia de flujo hacia el área lateral, las condiciones iniciales se mantienen.

Los términos de inercia convectiva, u ∂u/∂x, v ∂u/∂y, u ∂v/∂x, y v ∂v/∂y, a menudo se omiten en el modelado numérico porque la no linealidad de estos términos introduce dificultades adicionales. Varios autores han comentado sobre la necesaria presencia de los términos de inercia convectiva en el conjunto de ecuaciones para resolver adecuadamente el flujo secundario. Para probar esta conclusión, los cuatro términos de inercia convectiva se establecieron igual a cero. La Figura 3 muestra un gráfico a los 100 segundos de tiempo de simulación. La divergencia del flujo desde el canal hacia el área-lateral es fuerte; sin embargo, no se establece una circulación. A medida que el agua del canal llega al extremo aguas arriba del área lateral, el flujo se dirige inmediatamente hacia el área-lateral a lo largo de las paredes, lo que evita que se produzca la circulación.

En la literatura, el papel de la fricción en la circulación no está claramente definido. Para arrojar más luz sobre este tema, se realiza un experimento en el que los términos de fricción, f_r u (u ² + v ²)^1/2 / η - z_b y f_r v (u ² + v ²)^1/2 / η - z_b , se eliminan del cálculo. Los resultados de este experimento, incluidos los resultados cuantitativos detallados, son prácticamente indistinguibles de los resultados de línea de base (Fig. 2).

Bengtsson (2) ha documentado el efecto de un aumento en la profundidad del flujo en conexión con experimentos realizados en un modelo de lago. Su conclusión fue que la influencia de los términos de turbulencia horizontal se reducía al aumentar la profundidad. En este estudio, la dispersión horizontal de la cantidad de movimiento se simula mediante los términos de cierre de los esfuerzos efectivos, ∈ (∂²u /∂x² + ∂²u /∂y²) and ∈ (∂²v /∂x² + ∂²v /∂y²). Por lo tanto, no es obvio cómo debería afectar la profundidad a estos términos. Para investigar el efecto de la profundidad del flujo, se probaron profundidades que varía de 0.04 a 50 m, con la inestabilidad ocurriendo sólo para la profundidad de 0.04 m. Los resultados mostraron las siguientes tendencias: Las profundidades menores muestran una mayor divergencia de flujo desde el canal, mayores velocidades en la capa de corte y una producción más rápida de la circulación. En el extremo, sin embargo, la poca profundidad también está sujeta a inestabilidad. Las profundidades más grandes tienen menos transferencia de energía al área-lateral y, en consecuencia, poca o ninguna circulación.

Los primeros experimentos con la fricción parecen descartar la importancia que algunos autores le atribuyen. Sin embargo, todas estas pruebas se realizaron en problemas de escala relativamente pequeña. Para probar el efecto de la fricción en un problema de gran escala espacial, el tamaño de la configuración se incrementó a Δx = Δy = 100 m. La experiencia de las pruebas de análisis de estabilidad llevó al uso de un incremento de tiempo Δt = 100 segundos para acompañar el aumento de la escala espacila. En esta prueba, se utilizó el valor de fricción de la línea de base f_r = 0.0045. El flujo divergió inmediatamente hacia la área-lateral cerca de la pared aguas arriba, penetrando hasta el centro, antes de salir de la área-lateral a lo largo de la pared corriente abajo. No se desarrolló circulación en este experimento. El patrón de flujo fue muy similar al observado en la prueba en la que se despreció la inercia convectiva (Fig. 3).

En pruebas anteriores, se implementó una condición de velocidad de deslizamiento perfecto en todos los límites cerrados, con resultados satisfactorios. Para probar la validez de esta suposición, se realizó un experimento en el que el flujo está sujeto a una condición de velocidad nula como límite físico cerrado. Esta condición se puede aproximar estableciendo todas las velocidades ubicadas fuera de los límites físicos igual a cero. Para este experimento, una pendiente de fondo S_o = 0.0005 se introduce en la configuración del canal-área lateral. Las condiciones de límite abierto en los puntos finales del canal son niveles de agua que corresponden a la condición inicial de pendiente del lecho. Los límites cerrados quedan por definir mediante velocidades perpendiculares igual a cero. Todos los demás parámetros son los mismos que en la prueba de velocidad especificada, es decir, α = 0.1, Δx = Δy = 1 m, Δt = 1 sec, y f_r = 0.0045. El modelo antideslizante experimenta una fuerte amortiguación de la velocidad, aunque el desarrollo de la circulación es evidente después de 190 segundos de simulación.

El flujo secundario en expansiones repentinas es de naturaleza ligeramente diferente al sistema de canal-área lateral tratado anteriormente. Esto se debe en parte a la curvatura de la corriente hacia la expansión y al aumento de la exposición de las corrientes secundarias a los efectos de la corriente principal. Abbott y Rasmussen (1) desarrollaron un modelo de expansión de canale a partir del cual se presentaron resultados y conclusiones. Aquí se intenta verificar estas conclusiones utilizando una geometría similar.

En esta serie de pruebas, la configuración consta de un canal de entrada de 9 m de ancho y 7.5 m de largo, mientras que el canal expandido tiene 17 m de ancho y 22.5 m de largo. Una pendiente de fondo fijo de S_o = 0.0005 en la dirección del flujo del canal de entrada es especificado para toda la configuración. La condición inicial es una pendiente de la superficie del agua paralela al lecho a una profundidad de 2.5 m. Todas las velocidades se especifican en cero al comienzo de la simulación. Las condiciones de frontera abierta tanto en los extremos aguas arriba como aguas abajo son niveles de agua que coinciden con las condiciones iniciales. Los límites cerrados son velocidades nulas perpendiculares a las paredes. La fricción en este modelo está gobernada por un factor de fricción adimensional f_r = 0.0045. El factor de ponderación se establece en 0.1 mientras que el incremento de espacio es de 1 m y el incremento de tiempo es de 1 segundo. La Figura 4 es un gráfico de los resultados de la línea base de expansión del canal después de 100 segundos de simulación. Una circulación bien desarrollada forma una zona de separación en la esquina de la expansión. Las velocidades de entrada varían de 0.72 m/s en la pared inferior a 0.77 m/s en la pared superior, mientras que las velocidades de salida varían de 0.44 m/s a 0.30 m/s, de abajo hacia arriba. Los niveles de agua a lo largo de la simulación son continuos y estables. Se encuentran elevaciones ligeramente más bajas dentro del patrón de circulación.

En su mayor parte, la prueba de la expansión del canal produjo resultados consistentes con los de la configuración del canal-área lateral. Sin embargo, se encontró una discrepancia cuando se probaron los modelos de pendiente especificada sin modelar la tensión efectiva. En el modelo de agrupación de canales con velocidad especificada, la ausencia de las tensiones efectivas provocó que no se produjera circulación. Contrariamente a este resultado, ambas configuraciones, es decir, la expansión del canal y el sistema canal-área lateral, pueden generar un flujo secundario en espiral sin la presencia de las tensiones efectivas cuando una pendiente del lecho es la fuerza impulsora.

Surgió la pregunta de que si las corrientes secundarias que aparecen sin el beneficio de un modelado de tensión efectiva pueden ser de naturaleza estrictamente numérica. Teóricamente, los efectos numéricos deberían minimizarse cuando la discretización del dominio del problema se hace extremadamente pequeña. Con este fin, se redujeron los incrementos de espacio y tiempo en el modelo de expansión, aunque el tamaño del problema se mantuvo constante. Los valores de estos parámetros para esta prueba son Δx = Δy = 0.5 m y Δt = 0.5 sec.

Una superficie de agua horizontal sin velocidad se especifica como condición inicial. A medida que comienza la simulación, el nivel del aguas abajo se reduce en 40 pasos de tiempo hasta una profundidad de 2.5 m, la misma profundidad que la condición aguas arriba. Por lo tanto, una línea trazada a través de los niveles de agua del punto será paralela a la pendiente de fondo. El factor de ponderación para este experimento es cero, mientras que el factor de fricción adimensional es 0.0095. La Figura 5 es un gráfico de los vectores de velocidad después de 150 segundos de simulación. Una fuerte "circulación" en espiral, con un carácter similar a las observadas en experimentos anteriores con pendientes especificadas, se establece en la esquina de expansión.

6.  EVALUACIÓN

El programa de pruebas para este estudio es bastante extenso; por lo tanto, aquí solo se puede presentar una discusión limitada. Sin embargo. el análisis y evaluación de los experimentos numéricos se basa en todas las pruebas realizadas. Para una descripción más detallada, el lector se refiere a la Ref. l4.

El uso de niveles de agua especificados en los límites abiertos demostró ser una mejor condición de contorno que la velocidad especificada en las primeras series de pruebas. Cuando una diferencia en los niveles del agua es la fuerza impulsora para el flujo a través de la configuración, tanto la velocidad como la superficie del agua son estables y continuas, con pocas anomalías, si es que hay alguna. Esto contrasta con el modelo de velocidad especificada que requiere una condición inicial especial antes de que pueda comenzar la simulación. Además, las velocidades y los niveles de agua oscilantes afectan a cualquiera de las simulaciones de velocidad especificada.

Las diferencias específicas en el comportamiento del modelo debido a un cambio en las condiciones de contorno se encuentran sólo en la prueba de α, el factor de ponderación utilizado en la rutina de promediado de la velocidad. En el modelo de velocidad especificada, la circulación no ocurrió sin la presencia de los términos de cierre, ∈ (∂²u /∂x² + ∂²u /∂y²) y ∈ (∂²v /∂x² + ∂²v /∂y²), en los cálculos. Sin embargo, apareció un flujo secundario en espiral en todos los modelos inclinados cuando se probó sin que se representaran las tensiones efectivas. No parece que este resultado se produzca numéricamente, como lo demuestra la presencia constante de esta "circulación" a pesar del aumento en la resolución de la red.

Si bien se reconoce la condición de "no deslizamiento" en la naturaleza, la prueba de este modelo se ha realizado principalmente con una especificación de límite de "deslizamiento perfecto". Esta es una suposición razonable en modelos donde la resolución espacial a lo largo de un canal no es muy fina. En el experimento que involucró la especificación de velocidades cero fuera de la geometría del límite, resultaron efectos de resistencia abrumadores. Obviamente, cualquier consideración de una condición límite de no deslizamiento debe coordinarse con una reducción acompañante de los efectos de resistencia de fondo.

Los resultados del programa de pruebas son razonables y alentadores, a pesar de la presencia de dos defectos atribuibles a la representación de los esfuerzos efectivos. Primero, aún no se ha encontrado una base física por la cual elegir el factor de ponderación apropiado, α, en la rutina de promediado de velocidad. Hay casos en la literatura donde los procesos físicos han sido reemplazados con éxito por técnicas numéricas de manera general. Aunque la selección del factor de ponderación es actualmente una tarea de calibración manejable, aún no se ha avanzado un vínculo físico con el proceso de turbulencia.

El segundo inconveniente en la representación efectiva de la tensión es algo más grave que el primero. Gran parte del éxito en el cumplimiento del perfil de rasgos requerido por los términos de cierre se debe al efecto de la viscosidad numérica. A medida que aumenta el factor de ponderación, el modelo reacciona como si el fluido se volviera más viscoso, aumentando así el intercambio de impulso lateral y aumentando la amortiguación viscosa. Esencialmente, la viscosidad se usa para modelar un efecto de turbulencia. Por lo tanto, se debe tener cuidado al utilizar la rutina de promediado de velocidad. Debe lograrse un equilibrio entre la simulación de los esfuerzos efectivos y el cambio asociado en las propiedades del fluido.

Este estudio ha verificado experimentalmente la conclusión de Flokstra de que la verdadera circulación, es decir, un patrón de flujo que posee una zona de separación con líneas de corriente circulares cerradas, requiere el modelado de los esfuerzos cortantes efectivos. Un análisis de orden de magnitud realizado en los diversos términos de la ecuación de movimiento confirma la importancia de las tensiones efectivas en todos los casos en los que se produce la circulación. La circulación requiere un intercambio continuo de energía turbulenta a través de la capa de corte para mantenerse. La retirada de las tensiones efectivas después de que se ha establecido el patrón de flujo constante disuelve la circulación y finalmente conduce a la inestabilidad.

El análisis del orden de magnitud de los términos encontrados en la ecuación del movimiento muestra que la inercia convectiva es significativa en el canal y la capa de corte para todos los casos en los que se produce la circulación. La presencia de inercia permite que el flujo retenga una estructura uniforme por una distancia más allá de la ubicación de un cambio de configuración, lo que permite el desarrollo de una zona de separación adyacente a la extensión libre del flujo uniforme. En última instancia, esta separación de flujo se convierte en una zona local de flujo circulante.

La inclusión de la inercia convectiva en el modelo matemático no asegura la generación de flujo secundario. Incluso con la estipulación adicional de que las tensiones efectivas y todas las demás cantidades se describan con precisión, la circulación puede verse inhibida por efectos de fricción. En todos los casos en los que no se producen corrientes secundarias, el término de resistencia es significativo y mayor que los términos de inercia convectiva.

Este estudio ha encontrado que la fricción de fondo es el mayor impedimento para la existencia de flujo circulante. Parece existir una competencia entre la inercia convectiva y las fuerzas de resistencia del lecho. El hecho de que los términos de inercia convectiva contengan gradientes espaciales de velocidad los hace particularmente sensibles a los efectos de escala. En problemas de pequeña escala, las diferencias laterales de velocidad ocurren en distancias relativamente pequeñas, creando grandes gradientes de velocidad. Las grandes magnitudes de los términos de inercia convectiva hacen que los efectos de la resistencia del lecho sean insignificantes. Ningún factor de fricción razonable puede afectar este mecanismo. Por el contrario, los problemas a gran escala reducen la magnitud tanto de la inercia convectiva como de las tensiones efectivas a tal grado que los términos de fricción se promueven hasta el punto en que los efectos de resistencia inhiben totalmente la generación de flujo secundario.

Este modelo muestra al menos dos mecanismos diferentes de inestabilidad: no lineal y Courant. La inestabilidad no lineal se describe teóricamente como la incapacidad de resolver la energía de la malla espacial. Físicamente, la energía se distribuye en cascada a escalas cada vez más pequeñas por la acción de los términos no lineales en las ecuaciones de gobierno. En las escalas más pequeñas, la energía se disipa mediante efectos viscosos. La formulación discreta del modelo numérico interrumpe la cascada de energía a la resolución de la red; por lo tanto, la energía se acumula a esta escala y eventualmente estropea los cálculos.

La inestabilidad no lineal se caracteriza por el desarrollo gradual de discontinuidades en la superficie del agua acompañadas de un comportamiento similar en las velocidades calculadas. El proceso suele ser lento y puede tardar hasta 100 pasos en desarrollarse. En este modelo numérico, la inestabilidad no lineal requiere que la técnica de promediado de velocidad esté presente en todas las simulaciones, aunque el factor de ponderación no necesita ser grande. La mayoría de las corridas fueron estables con α = 0.1. Físicamente hablando, el uso de la rutina de promediar la velocidad introduce un mecanismo de disipación de viscosidad más fuerte en el fluido. La energía ya no debe transferirse a escalas más pequeñas que la resolución de la cuadrícula para que actúen los efectos viscosos.

La inestabilidad de Courant ocurre cuando la relación entre la celeridad física y la celeridad numérica (definida como el número de Courant) excede un valor característico. La celeridad física para este modelo es la velocidad máxima del canal, U_max, mientras que la celeridad numérica se define como Δx/Δt = Δy/Δt. Por tanto, el criterio es de la forma (U_max Δt /Δx) ≤ ε, en la cual ε es el límite característico. Las dos etapas explícitas contenidas en el procedimiento multioperativo son presumiblemente responsables de la condición de estabilidad de Courant encontrada en el presente modelo.

La inestabilidad de Courant es característicamente un proceso bastante rápido. La simulación avanza sin dificultad apreciable hasta que aparece una discontinuidad repentina en una de las variables dependientes. En unos pocos pasos, el cálculo se estropea. En este estudio, el valor límite del número de Courant depende del factor de ponderación utilizado en la rutina de promediado de velocidad. Esto es de esperar, ya que los factores de ponderación grandes pueden suavizar las inestabilidades que de otro modo se producirían si se utilizaran factores de ponderación más pequeños. Para α = 0.1, el número de Courant en este modelo debe ser menor o igual a 0.5.

7.  CONCLUSIONES Y RECOMENDACIONES

Las principales conclusiones de este estudio son las siguientes:

1. El modelado eficaz de esfuerzos cortantes es una condición necesaria para la resolución de una circulación constante y cerrada en los modelos matemáticos de dos dimensiones, promediados en profundidad.

2. La inercia convectiva debe incluirse en un análisis donde se estén considerando corrientes secundarias, es decir, flujos de circulación.

3. Existe una competencia entre la fuerza de inercia convectiva y la de resistencia del lecho. Salvo las fuerzas del viento, el flujo circulante sólo es posible cuando la resistencia del lecho tiene una influencia menor; por ejemplo, a escalas de longitud pequeñas.

4. La condición de velocidad nula en los límites físicos no es absolutamente necesaria. Sin embargo, si se especifica la condición de no deslizamiento, el aumento de los efectos de resistencia puede tener que corregirse reduciendo el factor de fricción utilizado en el modelado de la resistencia del lecho.

5. Para un problema dado, el tipo de condiciones de contorno tiene un efecto importante en los patrones de flujo resultantes.

Se ofrecen las siguientes recomendaciones para futuras investigaciones:

1. La mayor fuente de la incertidumbre es el modelado de los esfuerzos cortantes efectivos. Aunque los métodos simplificados para representar los esfuerzos efectivos han dado resultados razonables, será necesario un mayor nivel de sofisticación para resolver patrones de flujo complejos. En tales casos, puede justificarse una descripción separada de los tres componentes de los esfuerzos efectivos. En la actualidad, no se dispone de soluciones para este problema.

2. Se necesitan estudios adicionales para identificar los efectos numéricos de varios esquemas y las técnicas de discretización utilizadas para representar los límites físicos.

3. Si bien no beneficia directamente a la formulación de modelos matemáticos, la compilación de datos físicos sobre varios flujos de circulación sería fundamental para el desarrollo y prueba de modelos capaces de realizar una simulación de alta precisión.

AGRADECIMIENTOS

Este estudio fue posible gracias al proyecto de la National Science Foundation No. CME-7805458. Se agradece el apoyo de esta institución.

APÉNDICE I.  BIBLIOGRAFÍA

1. Abbott, M. B., y C. H. Rasmussen. 1977. "On the Numerical Modeling of Rapid Expansions and Contractions in Models that are Two-Dimensional in Plan," Paper A 104, 17th Congress of the International Association for Hydraulic Research, Baden-Baden, Germany, Vol. 2, 229-237.

2. Bengtsson, L. 1978. "Wind Induced Circulation in Lakes," Nordic Hydrology, Vol. 9, No. 2, Stockholm, Sweden, 75-94.

3. Flokstra, C. 1976. "Generation of Two-Dimensional Horizontal Secondary Currents," Reports S 163-II, Delft Hydraulics Laboratory, Delft, The Netherlands, July.

4. Flokstra, C. 1977. "The Closure Problem for Depth-Averaged Two-Dimensional Flow." Paper A106, 17th Congress of the International Association for Hydraulic Research, Baden-Baden, Germany, Vol. 2, 247-256.

5. Forester, C. K. 1977. "Higher Order Monotonic Convective Difference Schemes," Journal of Computational Physics, Vol. 23, 1-22.

6. Hansen, W. 1962. "Hydrodynamic Methods Applied to Oceanographic Problems," Proceedings of the Symposium on Mathematical-Hydrodynamical Methods of Physical Oceanography, Institute für Meereskunde der Universität Hamburg, Hamburg, Germany, 25-34.

7. Kuipers, J., y C. B. Vreugdenhil. 1973. "Calculations of Two-Dimensional Horizontal Flows," Report S 163-I, Delft Hydraulics Laboratory, Delft, The Netherlands, Oct.

8. Launder, B. E., y D. B. Spalding, 1974. "The Numerical Computation of Turbulent Flows," Computational Methods in Applied Mechanical Engineering, Vol. 3, 269-289.

9. Lean, G. H., y T. Weare. 1979. "Modeling Two-Dimensional Circulating Flow," Journal of the Hydraulics Division, ASCE, Vol. 105, No. HYI, Proc. Paper 14312, Jan., 17-26.

10. Leendertse, J. J. 1967. "Aspects of a Computational Model for Long-Period Water Wave Propagation," RM-5294-PR, The Rand Corporation, Santa Monica, Calif., May.

11. Leendertse, J. J. 1970. "A Water Quality Simulation Model for Well-Mixed Estuaries and Coastal Seas," Vol. I, Principles of Computation," RM-6230-RC, The Rand Corporation, Santa Monica, Calif., Feb.

12. McGuirk, J. J., y W. Rodi. 1978. "A Depth-Averaged Mathematical Model for the Near Field of Side Discharges into Open Channel Flow," Journal of Fluid Mechanics, Vol. 86, Part 4, London, England, 761-781.

13. Platzman, G. W. 1959. "A Numerical Computation of the Surge of 26 June 1954 on Lake Michigan," Geophysics, Vol. 6, No. 3-4, 407-438.

14. Ponce, V. M., y S. B. Yabusaki. 1980. "Mathematical Modeling of Circulation in Two-dimensional Plane Flow," Report CER7940VMDSBY59, Civil Engineering Department, Engineering Research Center, Colorado State Univessity, Fort Collins, Colo., June.

15. Weare, T. J. 1976. "Instability in Tidal Flow Computational Schemes," Journal of the Hydraulics Division, ASCE, Vol, 102, No. HY5, Proc. Paper 12100, May, 569-580.