1. INTRODUCCIÓN
El modelado matemático de cuencas hidrográficas está bien establecido en la investigación y la práctica hidrológica (1, 5, 6, 8, 20). Entre los diversos aspectos del modelado de cuencas hidrográficas, la conversión del exceso de lluvia a escorrentía es quizás la que ha recibido mayor atención. Históricamente los procedimientos para lograr esto recurren a la teoría de la onda cinemática (11).
La onda cinemática es una herramienta valiosa en la simulación de cuencas hidrográficas. Con las pendientes pronunciadas que se encuentran generalmente en la cabecera de las cuencas, las condiciones de flujo son tales que las ondas cinemáticas son aproximaciones razonables.
Los procedimientos para los cálculos de ondas cinemáticas pueden ser analíticos o numéricos.
En esquemas de segundo orden, la difusión numérica desaparece pero aún subsiste una cierta cantidad de dispersión numérica (de tercer orden) (16). La búsqueda de un esquema que presente difusión y dispersión numérica nulas puede es poco aconsejable, porque la solución en sí misma se benefícia de estas contribuciones. En efecto, se ha demostrado que la onda de difusión se aplica a una clase más amplia de problemas que la onda cinemática (13). Por lo tanto, una pequeña cantidad de difusión numérica en la solución de onda cinemática es ciertamente favorable.
El objetivo debe ser "controlar" la cantidad de difusión numérica de tal manera que coincida con la difusión física. Como se muestra aquí, esta metodología tiene la ventaja de que la respuesta de la cuenca es esencialmente independiente del tamaño de la malla. Esta última característica mejora sustancialmente la credibilidad de los resultados, lo que lleva a una mejor práctica de modelado.
2. ANTECEDENTES
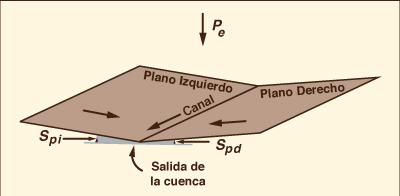
El modelado matemático distribuido de la dinámica de cuencas hidrográficas se ha intentado de varias maneras (1, 5, 6, 8, 19, 20). Una formulación ampliamente aceptada es la elección de la ecuación de la onda cinemática junto con una representación espacial simplificada de la cuenca en forma de "libro abierto". Tal configuración consta de dos planos adyacentes a un canal (Fig. 1).
Una fuente de incertidumbre en este tipo de modelado es la exactitud del valor estimado de fricción. El flujo sobre los planos suele ser de profundidades tan pequeñas que es posible que prevalezca el flujo laminar. Por el contrario, es probable que el flujo en el canal sea turbulento. Las ecuaciones de onda cinemática son una opción común en la simulación de flujo en cuencas. Estas ecuaciones están bien establecidas y generalmente conducen a soluciones físicamente realistas, sin las complejidades numéricas y de otro tipo que suelen ser parte de las formulaciones de ondas dinámicas completas. Para derivar la ecuación de la onda cinemática, el enunciado usual de conservación de la masa en un volumen de control se combina con una forma simplificada de conservación de la cantidad de movimiento que sólo tiene en cuenta las fuerzas de fricción y del volumen (masa). El enunciado de conservación de la masa es el siguiente:
en el cual Q = caudal, en m3/s; A = área, en m2; y qL = flujo lateral, en m3/s/m. El enunciado simplificado de la cantidad de movimiento es: So = Sf , en el cual So = pendiente de fondo, y Sf = pendiente de fricción. De hecho, éste es un enunciado del flujo uniforme, que conduce a una forma alternativa de expresar la cantidad de movimiento:
en el cual α y β son un coeficiente y un exponente, respectivamente. Los valores de α y β contienen información sobre las características de fricción y sección transversal [por ejemplo, β = 3 para un canal ancho con fricción laminar; β = 5/3 para un canal ancho con fricción de Manning; β = 3/2 para un canal ancho con fricción de Chézy; y β = 4/3 para un canal triangular con fricción de Manning (11)]. La velocidad de propagación de las ondas cinemáticas se obtiene de la Ec. 2:
en la cual c = celeridad de la onda cinemática; y v = velocidad media del flujo. La ecuación de onda cinemática se obtiene multiplicando las Ecs. 1 y 3 y haciendo uso de la regla de la cadena para obtener:
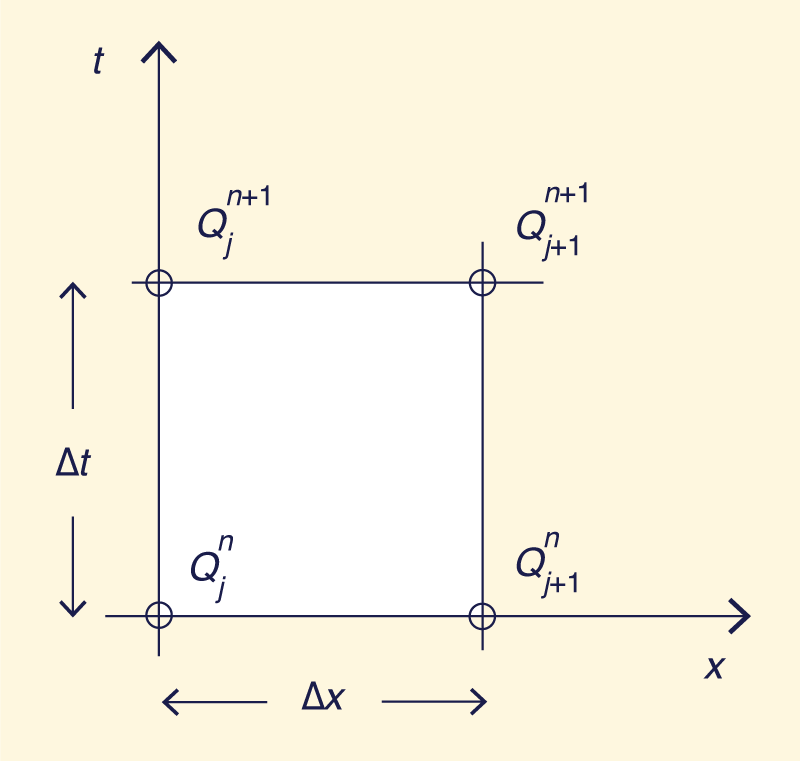
La Ecuación 4 contiene términos de convección en el lado izquierdo y un término fuente en el lado derecho. Significativamente, la Ec. 4 no contiene un término de difusión. Esta ecuación puede resolverse por métodos analíticos o numéricos. Una clase típica de soluciones numéricas es aquélla en la cual los valores de ∂Q/∂t, ∂Q/∂x, c y qL se expresan en términos de todos o algunos de los cuatro valores discretos adyacentes de Q, c y qL en el espacio y tiempo (Fig. 2). Alternativamente, el valor de c podría mantenerse constante, lo cual da lugar a la solución lineal de la onda cinemática.
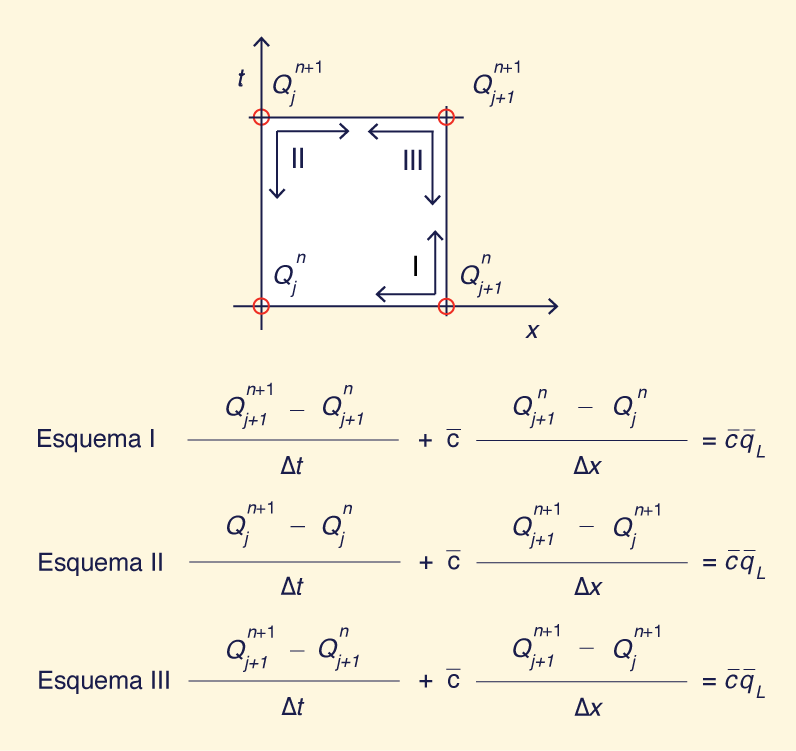
Una solución numérica de la Ec. 4 siguiendo el procedimiento antes mencionado no está exento de inconvenientes. A menos que las derivadas espaciales y temporales están perfectamente centradas en la malla, se generará una cierta cantidad de difusión en la solución numérica (Fig. 2). Los esquemas totalmente descentrados siguen siendo populares entre los profesionales (6, 7, 10). Ponce et. al. (16) han demostrado que de los tres posibles esquemas totalmente descentrados (ver Fig. 3), los esquemas I y II son condicionalmente estables y convergentes a la solución analática en cuanto el número de Courant (definido como la relación entre la celeridad física c y la celeridad de la malla Δs/Δt) se aproxime a 1. El esquema I, estable para números de Courant menores o iguales a 1, equivale a "diferenciación a barlovento". El esquema II, estable para números de Courant mayores o iguales a 1, es exactamente la imagen opuesta del esquema I. El esquema III es incondicionalmente estable, pero no convergente para cualquier valor del número de Courant (16).
Los esquemas I y II son complementarios, con versiones en amplio uso, por ejemplo, en la opción de enrutamiento de la onda cinemática utilizada en los modelos HEC-1 y su secuela, HEC-HMS (6). El esquema III (y varias versiones relacionadas), aunque no convergente, también se ha visto favorecido por su característica de estabilidad incondicional (7, 10). En cualquier aplicación práctica, es probable que los números de Courant locales varíen y sean diferentes de 1. En este caso, ninguno de estos tres esquemas resolvería la ecuación de la onda cinemática, y ciertamente no el esquema III, dada su demostrada falta de convergencia. En teoría, para números de Courant cercanos a 1, en cuanto la discretización se hace extremadamente pequeña, los esquemas I y II pueden aproximarse asintóticamente a la solución analítica de la ecuación de la onda cinemática. Con las potentes computadoras de hoy, esto es ciertamente una posibilidad. Sin embargo, la preocupación subsiste si la eliminación completa de la difusión numérica es la estrategia apropiada para este tipo de problema. En resumen, el modelador hidrológico se enfrenta al siguiente dilema: si busca eliminar la difusión numérica a cualquier costo, la solución puede ser puramente cinemática y, por lo tanto, carecer de la propiedad de difusión natural inherente a los flujos físicamente realistas. Por otro lado, si el modelador usa un esquema totalmente descentrado como I, II o III, el resultado final serí una cantidad incontrolada de difusión numérica que sólo se asemejarí vagamente al proceso físico de difusión. La solución de esta dificultad es "igualar" razonablemente las difusiones física y numérica, un procedimiento que se ha utilizado con éxito en el enrutamiento del flujo en canales y otras aplicaciones (9, 14, 18). La clara ventaja de este enfoque es que hace que la solución numérica sea esencialmente independiente del tamaño de la malla. En otras palabras, la convergencia se satisface con una malla mucho más gruesa que para los esquemas I o II. Dada la variación natural en los números de Courant que probablemente están presentes en aplicaciones prácticas, un método que converje para una amplia gama de tamaños de malla es ciertamente uno a tener muy en cuenta.
3. FORMULACIÓN DE LA ONDA DIFUSIVA
La solidez del método de "igualación de difusividades" se ilustra aquí comparando los resultados de dos soluciones para la dinámica de la cuenca. La primera es una aplicación del esquema III a la ecuación de onda cinemática, Ec. 4, con el efecto de difusión numérica estando "descontrolado".
La aplicación del esquema III a la Ec. 4 en un modo lineal conduce a la siguiente ecuación de enrutamiento:
en la cual C0 = C/(1 + C); C2 = 1/(1 + C); y QL = flujo lateral promedio, C = número de Courant de la celda computacional, C = c (Δt /Δs), en la cual Δs es Δx o Δy. Para los cálculos de flujo superficial, QL es el producto de la precipitación neta por el área de la celda. Para el enrutamiento en el canal, QL es la contribución lateral promedio en el tiempo, integrada a lo largo de la longitud de una celda. Con una estimación de la celeridad media de onda para el plano y el canal, junto con la especificación adecuada de las condiciones iniciales y de contorno, la Ec. 5 permite el cálculo de la respuesta de la cuenca para una precipitación neta dada. La derivación del método de igualación de difusividades es paralela a la del método Muskingum-Cunge, con la adición de flujo lateral (3, 14, 15). Las ecuaciones de enrutamiento son las siguientes:
en la cual C0 = (-1 + C + D)/(1 + C + D); C1 = (1 + C - D)/(1 + C + D); C2 = (1 - C + D)/(1 + C + D);
en el cual q = flujo unitario (q = vd; d = profundidad de flujo); So = pendente de fondo; c = celeridad de la onda cinemática, y Δs = tamaño de la malla. Debe tomarse en cuenta que hay grandes diferencias entre las Ecs. 5 y 6 con respecto a sus requisitos de datos. La ecuación 5 requiere sólo valores de c tanto para el plano como para el canal (o alternativamente: la velocidad media v y un valor adecuado de β, ver la Ec. 3). De otro modo, la Ec. 6 requiere valores de c, q y So tanto para el plano como para el canal (o alternativamente: β, v, d, y So ). Dado que la difusividad física es v = q /(2So), se deduce que, a diferencia de la Ec. 6, la Ec. 5 no contiene ninguna información física al respecto de difusión. Sin embargo, no es sorprendente que la aplicación de la Ec. 5 muestra un comportamiento similar a la difusión. Esta última no está relacionada con el problema físico, es directamente atribuible al tamaño de la malla, y es una función de éste. 4. FORMULACIÓN DE ONDA DIFUSIVA CON COMPONENTE DINÁMICO
El análisis anterior ha demostrado las ventajas de utilizar la onda difusiva en lugar de la onda cinemática en el modelado de la respuesta de una cuenca. Aparte del supuesto de linealidad,
en la cual F = número de Froude, definido como F = v/(gd)1/2, y g = aceleración de la gravedad.
La ecuación 8 se puede generalizar para cualquier formulación de fricción y forma de sección transversal considerando que el número de Froude de estabilidad neutra es igual a 1/(β - 1).
Dada la ecuación 9, se puede formular un modelo de onda difusiva con componente dinámico en base a la Ec. 6, con la Ec. 7 modificada para tener en cuenta el número de Froude y la dependencia de β de la difusividad física, Ec. 9. En efecto, para la onda de difusión con componente dinámico, la Ec. 7 se modifica a lo siguiente:
Con el número de Reynolds de la malla definido con la Ec. 10, la Ec. 6 representa una descripción lo más completa posible de la dinámica de las ondas, dentro del contexto de una formulación difusiva lineal. Sin embargo, la utilidad de la Ec. 10 en comparación con la Ec. 7 dependerá de si los fenómenos no permanentes que se están simulando se pueden interpretar correctamente como una onda dinámica (13). La experiencia indica que para una gran clase de problemas de interés práctico en hidrología, la escala de ondas bien puede estar en el rango de la onda difusiva, o aún cinemática. 5. EJEMPLO ILUSTRATIVO Las metodologías descritas en la sección anterior se comparan aquí aplicándolas a un problema típico de dinámica de cuencas. Siguiendo un uso generalizado, el esquema de la Ec. 5 se denomina "onda cinemática", aunque se reconoce su difusión numérica apreciable e incontrolada. El método de "igualdad de difusividades", Ecs. 6 y 7, se denomina en el presente artículo "onda de difusión". La onda de difusión con componente dinámico, Ecs. 6 y 10, aunque propiamente dentro de la familia de modelos de onda difusiva, se denomina aquí "onda dinámica" (véanse las Tablas 2 y 3). El ejemplo consiste en una cuenca conceptualizada como un libro abierto con dos planos adyacentes a un canal (Fig. 1). Se asume que los planos son impermeables, con un exceso de precipitación igual a la precipitación total. El flujo de entrada a los planos es el exceso de precipitación y la escorrentía es por flujo laminar superficial en una dirección perpendicular al alineamiento del canal. El flujo de entrada al canal es por contribución lateral de los planos y el flujo de salida del canal es la respuesta de la cuenca.
Las dimensiones son las siguientes: longitud del plano (en la dirección del flujo en plano) = 120 pies (36.58 m); ancho del plano = 240 pies (73.15 m); longitud del canal = 240 pies (73.15 m).
El flujo laminar en los planos y el flujo turbulento en el canal se calculan siguiendo las prácticas establecidas en la hidráulica (2). Las condiciones de flujo promedio en los planos son: descarga por unidad de ancho qp= 0.004 pies2/s (0.00037
m2/s); velocidad media vp = 0.5 pies/s (0.15 m/s);
profundidad media de flujo dp = 0.008 pies (0.0024 m); exponente de la curva de gasto (flujo laminar en secciones hidráulicamentes anchas) βp = 3; y celeridad media de la onda cp = 1.5 pies
Estos cálculos conducen a un tiempo de concentración tc = (120 pies/1.5 pies)
+ (240 pies/4 pies) = 140 s. Por lo tanto, se elige una duración de tormenta de 3 min para asegurar el logro del equilibrio en la salida de la cuenca. El volumen total de lluvia es de 0.15 pulg. (3.81 mm), o 720 pies3
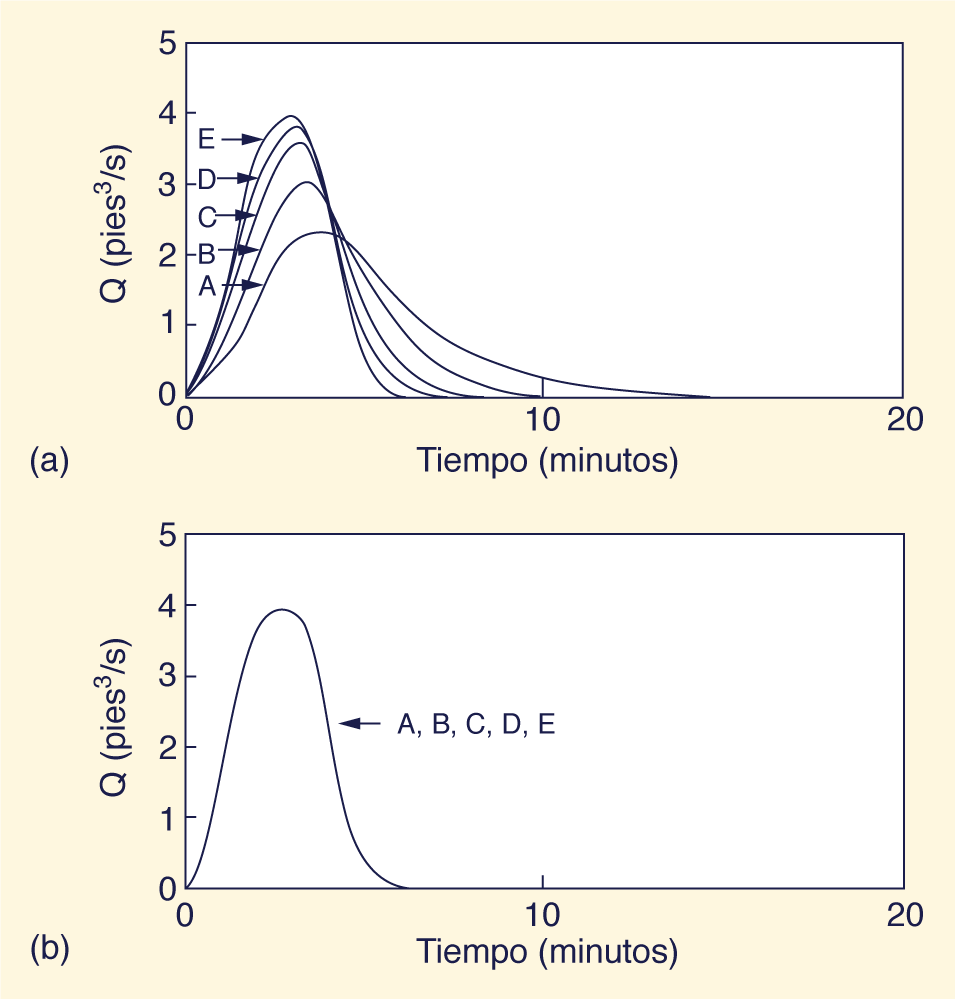
6. RESULTADOS Los tres métodos se probaron con respecto a su comportamiento con varios niveles de resolución de malla. Se eligieron cinco niveles de resolución, que varían de muy grueso a muy fino, como se muestra en la Tabla 1. Los resultados de las simulaciones se muestran en las Tablas 2 y 3, expresados en términos de: (1) flujo máximo; y (2) tiempo pico. La Figura 4 muestra los hidrogramas calculados para: (1) método cinemático (Esquema I); y (2) método difusivo (igualación de difusividades). Como era de esperar, los resultados del método cinemático variaron sustancialmente con la resolución de la malla. Con una resolución muy gruesa (A), el flujo máximo fue de 2.3507 pies3/s (0.0666 m3/s), mientras que para una resolución muy fina (E), el flujo máximo fue de 3.9641 pies3/s (0.1122 m3/s). Los resultados del método difusivo mostraron propiedades de convergencia mucho mejores que el método cinemático. Con una resolución muy gruesa (A), el flujo máximo fue de 3.9336 pies3/s (0.1113 m3/s), mientras que para una resolución muy fina (E), fue de 3.9971 pies3/s (0.1132 m3/s). Se concluye que el método difusivo proporciona independencia de malla para una amplia gama de niveles de resolución, mientras que esto no es el caso del método cinemático. La demostrada independencia de malla del método difusivo es decididamente una ventaja.
Los resultados del método dinámico no se representaron en la Fig. 4 debido a su gran parecido con los del método difusivo (ver Tablas 2 y 3). Esta semejanza subraya la falta de una contribución dinámica significativa en el ejemplo mostrado. El criterio adimensional de Ponce et. al. (13) se puede utilizar para demostrar si la onda es realmente una onda difusiva. Según este criterio, la onda es difusiva si se satisface la siguiente desigualdad:
en la cual T = escala de tiempo representativa de la onda de avenida. En este caso, se puede suponer que la escala de tiempo es igual al doble de la duración de la precipitación T = 360 s. Para el flujo del canal, con So = 0.01 y d = 0.333 pies (0.1 m), la Ec. 11 conduce a un lado izquierdo que tiene un valor de 35.4, satisfaciendo así la desigualdad. Esto explica por qué la solución de onda dinámica no es muy diferente de la solución de onda difusiva para este problema en particular. La conservación de la masa se controló mediante la integración de los hidrogramas de flujo de salida para todos los ensayos descritos en las Tablas 2 y 3. Todos los métodos y ensayos conservaron la masa (volumen) en un 100%. Además, se utilizó el método difusivo con niveles de resolución espacial que satisfacen los criterios de precisión correspondientes (17). En suma, cabe señalar que si la discretización se hubiera hecho extremadamente pequeña, los caudales máximos calculados por los métodos difusivo y dinámico (ver Tablas 2 y 3) habráan convergido al valor de flujo máximo obtenido al concentrar el flujo en la salida, es decir 4 pies3/s (0.1132 m3/s). Esto se atribuye al hecho de que la translación (es decir, la convección) es el mecanismo físico predominante para el ejemplo dado, y la difusión juega un papel relativamente mucho menor. Por lo tanto, un método difusivo (y difusivo con componente dinámico) en el que la difusión es pequeña y controlada con parámetros físicos es ciertamente preferible a un método cinemático en el que la difusión numérica podría ser excesiva y no tener relación con la física del problema.
7. RESUMEN Y CONCLUSIONES
Se formula un método de ondas difusiva para calcular la dinámica de las cuencas hidrográficas. A diferencia de los esquemas descentrados, el esquema de onda difusiva se formula igualando las difusividades física y numérica. Esto da como resultado un control efectivo de la difusión numérica y conduce a simulaciones que son esencialmente independientes del tamaño de la malla. El método de la onda difusiva se amplía al ámbito de las ondas dinámicas al incluir la dependencia del número de Froude de la difusividad física. La formulación resultante representa una descripción lo más completa posible de la dinámica de las ondas dentro del marco de la teoría de las ondas difusivas.
Los tres métodos: (1) cinemático, con difusión numérica incontrolada; (2) difusión, con difusividades físicas y numéricas iguales; y (3) dinámicos, con difusividad dependiente del número de Froude, se prueban para convergencia y precisión general. Se muestra que el método difusivo tiene propiedades de convergencia mucho mejores que el método cinemático. En particular, la demostrada independencia de la malla del método difusivo es una ventaja a tener en cuenta.
APÉNDICE I. REFERENCIAS
APÉNDICE II. NOTACIÓN En este artículo se utilizan los siguientes símbolos:
A = área de flujo; C = número de Courant, C = c Δt /Δs; c = celeridad de la onda; D = número de Reynolds de la malla, Ec. 7; d = profundidad del flujo; F = número de Froude; g = aceleración de la gravedad; j = índice de discretización espacial; n = índice de discretización temporal; Q = caudal, descarga; QL = flujo promedio de entrada lateral ; q = descarga de ancho unitario; qL = flujo de entrada lateral, por unidad de longitud del canal; Sf = pendiente de fricción; So = pendiente del lecho (o de fondo); s = variable espacial, ya sea x or y; Δs = intervalo de espacio, ya sea Δx o Δy; T = escala de tiempo representativa de los fenómenos no permanentes; t = variable de tiempo; tc = tiempo de concentración; v = velocidad media del flujo; x = variable espacial en la dirección paralela al flujo sobre los planos; Δx = intervalo de espacio en la dirección x; y = variable espacial en la dirección paralela al flujo en el canal; Δy = intervalo de espacio en la dirección y; α = coeficiente de la curva de gasto, Ec. 2; y β = exponente de la curva de gasto, Ec. 2.
Subíndices c = canal; y p = plano
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 220101 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |