1.  INTRODUCCIÓN

El rendimiento de agua de una cuenca es un problema fundamental en hidrología, refiriéndose al volumen de agua disponible en la salida durante un período de tiempo especificado. El rendimiento se expresa en términos de períodos mensuales, estacionales o anuales. Existen varios enfoques para el cálculo del rendimiento hídrico. Estos varían en complejidad, desde fórmulas empíricas simples hasta modelos complejos basados ​​en simulación continua. En tanto que las fórmulas empíricas tienen una aplicabilidad limitada (Sutcliffe y Rangeley, 1960; Woodruff y Hewlett, 1970), los modelos de simulación continua requieren grandes cantidades de datos para su funcionamiento (Crawford y Linsley, 1966). Una alternativa práctica está representada por modelos conceptuales que utilizan la ecuación del balance hídrico (o balance hidrológico) para separar la precipitación en sus diversos componentes (Hamon, 1963).

En este artículo desarrollamos un modelo conceptual de balance hídrico anual, adecuado para su aplicación a una amplia gama de condiciones climáticas. El modelo separa la precipitación anual en sus tres componentes principales: escorrentía superficial, flujo base y vaporización. Se basa en una aplicación secuencial de dos pasos de una relación proporcional que une dos variables X e Y, de manera que la diferencia Z = X - Y alcanza asintóticamente un límite superior a medida que X e Y crecen sin límites. La forma genérica de la relación proporcional tiene dos parámetros: λ, el coeficiente de abstracción inicial, y Z_p, el valor potencial de Z = X - Y. Las pruebas iniciales con los datos de L'vovich (1979) muestran que el modelo es aplicable a una amplia gama de entornos climáticos.

2.  ECUACIONES DE BALANCE HÍDRICO

Una ecuación de balance hídrico aplicable a una tormenta dada es:

P = Q + L

(1)

en la cual P = precipitación, Q = escorrentía superficial y L = pérdidas o abstracciones hidrológicas (en milímetros, centímetros o pulgadas). Las pérdidas de una tormenta dada consisten en interceptación, almacenamiento en superficie, e infiltración.

Una ecuación de balance hídrico aplicable en una base anual es:

P = R + E

(2)

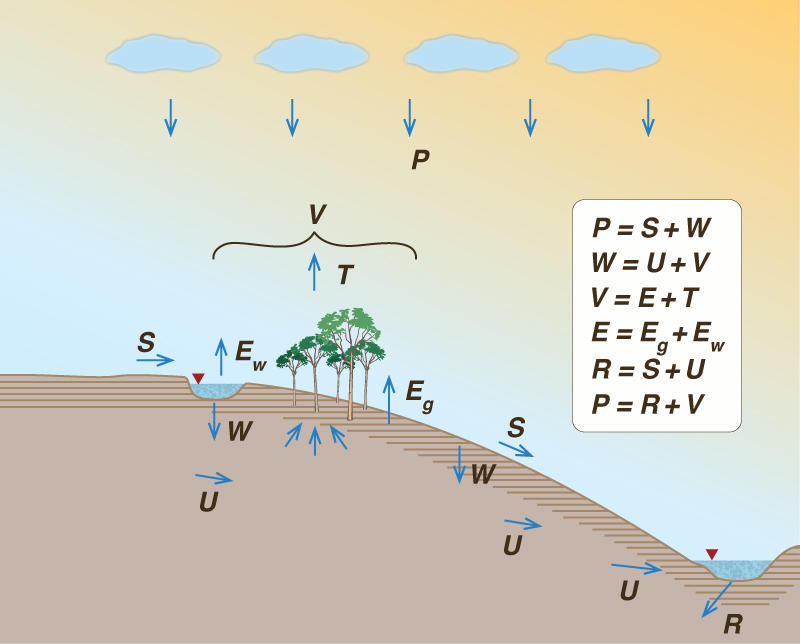
en la cual P = precipitación, R = escorrentía, incluida escorrentía superficial y subterránea, y E = evapotranspiración (en milímetros, centímetros o pulgadas). En esta ecuación, el término 'evapotranspiración' comprende los tres tipos de humedad evaporada: (1) evaporación de superficies con vegetación, es decir, evapotranspiración, (2) evaporación de superficies sin vegetación (suelo descubierto) y (3) evaporación de cuerpos de agua.

Las Ecuaciones 1 y 2 son modelos simplificados de un segmento del ciclo hidrológico. Por ejemplo, la Ec. 1 no describe la porción de almacenamiento superficial que eventualmente puede infiltrarse en el suelo. Asimismo, la Ec. 2 no describe explícitamente la humedad del suelo, que se incluye tanto en la escorrentía como en la evaporación. Siguiendo a L'vovich (1979), el balance hídrico anual de una cuenca se explica de mejor manera utilizando un conjunto de ecuaciones, como se describe a continuación.

La precipitación anual P se divide en dos componentes (Fig.1):

P = S + W

(3)

en la cual S = escorrentía superficial, es decir, la fracción de la escorrentía que se origina en la superficie, y W = humectación, es decir la fracción de precipitación que no contribuye a la escorrentía superficial. (Tengase en cuenta que la Ec. 3 es el equivalente anual de la Ec. 1).

Fig. 1  Elementos del balance hídrico.

Asimismo, la humectación consiste de dos componentes:

W = U + V

(4)

en la cual U = flujo base, es decir, la fracción de humectación que exfiltra hacia las corrientes vecinas, constituyendo el flujo en períodos no lluviosos, y V = vaporización, la fracción de humectación que regresa a la atmósfera como vapor de agua (Lee, 1970). La percolación profunda, es decir, la parte de la humectación que no contribuye al flujo base o a la vaporización, es una fracción muy pequeña de la precipitación [un promedio global de menos del 1,5%, según L'vovich (1979)], y se desestima aquí por motivos prácticos.

La vaporización, la cual comprende toda la humedad regresada a la atmósfera, tiene dos componentes:

V = E + T

(5)

en la cual E = evaporación no productiva, en lo sucesivo denominada "evaporación", y T = evaporación productiva, es decir, la resultante de la transpiración de la planta, en lo sucesivo denominada "evapotranspiración".

La evaporación tiene dos componentes: (1) E_n, evaporación de áreas no vegetadas de la superficie y cerca de la superficie, es decir, de suelo descubierto y del almacenamiento en pequeños cuerpos de agua (charcos); (2) E_w, evaporación de grandes cuerpos de agua considerables como lagos, ríos y embalses. La evapotranspiración es la evaporación de las superficies con vegetación, como las hojas y otros componentes de las plantas, lo cual es una función de la necesidad fisiológica de éstas de bombear humedad del suelo para mantener la turgencia y aprovechar los nutrientes.

De las Ecuaciones 3, 4 y 5, la escorrentía consta de dos componentes:

R = S + U

(6)

Asimismo, la precipitación P consta de dos componentes:

P = R + V

(7)

La Ec. 7 es análoga al conocido balance hídrico anual, Ec. 2. Sin embargo, la Ec. 7 se prefiere aquí, porque el término 'vaporización' identifica claramente las tres fuentes de humedad evaporada (Ec. 5).

Las Ecuaciones 3-7 constituyen un conjunto de ecuaciones de balance hídrico. La combinación de las Ecs. 6 y 7 conduce a los siguiente:

P = S + U + V

(8)

es decir, la precipitación anual se divide en sus tres componentes principales: escorrentía superficial, flujo base y vaporización. Cabe notar que la Ec. 8 asume que el cambio en el almacenamiento de humedad del suelo de un año a otro es despreciable, una suposición que es útil como primera aproximación.

Las Ecuaciones 4 y 7 permiten la definición de coeficientes de balance hídrico. El coeficiente de flujo base es (L'vovich, 1979):

U            U Ku = ____ = ________          W        U + V

(9)

y el coeficiente de escorrentía es:

R           R Kr = ____ = ________          P         R + V

(10)

Estos coeficientes varían en función del clima predominante, teóricamente dentro del rango 0-1. El clima predominante se caracteriza por la circulación atmosférica global del viento, latitud y altitud medias, aspecto, geomorfología, proximidad al océano, tipo de vegetación y uso de la tierra. En las regiones áridas y semiáridas, los coeficientes de balance hídrico son bajos, típicamente menores de 0.2, y pueden acercarse a cero en climas hiperáridos. En las regiones tropicales húmedas, los coeficientes son altos, a menudo superiores a 0.5, y el coeficiente de escorrentía K_r se acerca a 1 en algunos casos inusuales de extrema humedad (L'vovich, 1979). Sin embargo, hay excepciones, como un pantano o marisma (humedal), donde K_r es típicamente un valor bajo debido al mayor potencial de evapotranspiración.

3.  MODELO CONCEPTUAL

Una característica importante de las ecuaciones de balance hídrico (las Ecs. 3-7) es que todas tienen la misma estructura, en la que una cantidad X se expresa como la suma de dos componentes Y y Z:

X = Y + Z

(11)

L'vovich (1979) ha demostrado que la Ec. 3 se puede modelar mediante una relación proporcional tal que la humedad alcance asintóticamente un límite superior (W → W_p) a medida que la precipitación y la escorrentía superficial aumentan sin límites (P → ∞; S → ∞). Se observa que una relación similar es la base del modelo del número de la curva SCS, que resuelve la Ec. 1 (Servicio de Conservación de Suelos del Departamento de Agricultura de los Estados Unidos (USDA SCS), 1985). L'vovich (1979) también ha demostrado que la Ec. 4 puede modelarse mediante el mismo tipo de relación, es decir, una en la cual la vaporización alcanza un límite superior asintóticamente (V → V_p) a medida que la humedad y el flujo base aumentan sin límites (W → ∞; U → ∞). De esta manera, se logra la separación secuencial en dos pasos de la precipitación anual en sus tres componentes principales, escorrentía superficial, flujo base y vaporización.

La forma genérica de la relación proporcional es, según el modelo SCS (USDA SCS, 1985):

X - λ' Zp' - Y              Y _______________ = ____________           Zp'                X - λ' Zp'

(12)

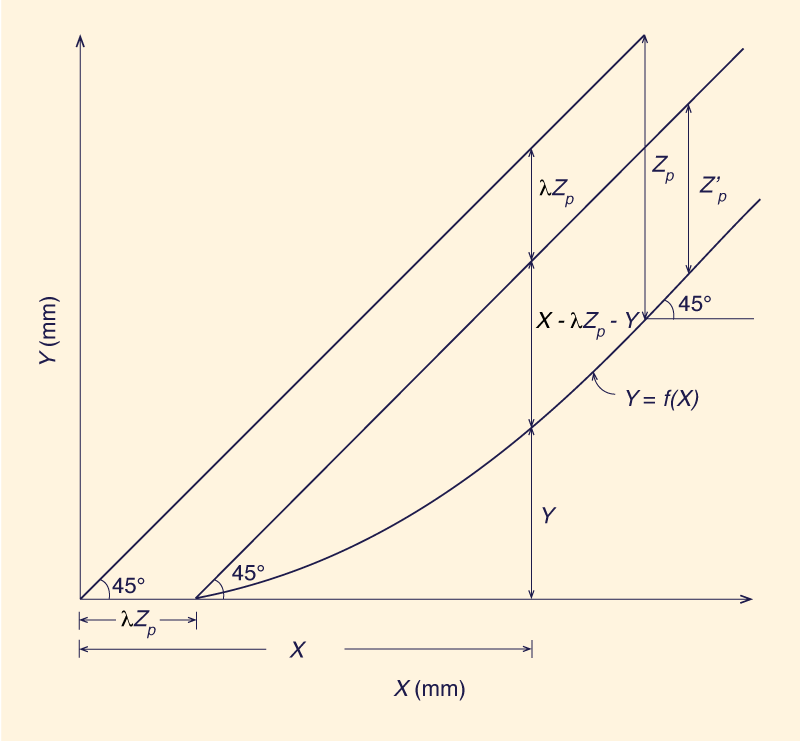
en la cual Y = f(X) y λ' es el coeficiente de abstracción inicial. La abstracción inicial es I_a = λ' Z_p', en la que Z_p' es el valor potencial de Z', es decir, un límite superior a Z' = X - λ' Z_p' - Y.

En este artículo, la abstracción inicial se define alternativamente como I_a = λ Z_p en la que Z_p es el valor potencial de Z = X - Y (Fig. 2). Esto conduce a una forma ligeramente modificada de la relación proporcional:

X - λ Zp - Y               Y _______________ = ____________       (1 - λ)Zp             X - λ Zp

(13)

Fig. 2   Esquema de definición del coeficiente de abstracción inicial λ y potencial Zp.

La Ecuación 13 tiene una ventaja significativa sobre la Ec. 12. A diferencia de λ', que no tiene límite superior teórico, λ está limitado en el rango 0 ≤ λ ≤ 1. El coeficiente de abstracción inicial λ es adimensional; las unidades de Z_p son las de X e Y (milímetros, centímetros o pulgadas).

Para el caso especial de abstracción inicial cero (λ = 0), la Ec. 13 se reduce a:

X - Y          Y _________ = ____       Zp           X

(14)

Resolviendo la Ec. 13 para Y = f(X) conduce a:

(X - λ Zp)2 Y = __________________           X + (1 - 2λ) Zp

(15)

sujeto a X > λ Z_p; Y = 0 en caso contrario.

Usando la Ec. 15, el submodelo de escorrentía superficial es:

(P - λs Wp)2 S = ____________________           P + (1 - 2λs) Wp

(16)

sujeto a P > λ_sW_p, y S = 0 en caso contrario, donde λ_s es el coeficiente de abstracción inicial de la escorrentía superficial. De la Ec. 3,

W = P - S

(17)

Asimismo, el submodelo de flujo base es:

(W - λu Vp)2 U = ____________________           W + (1 - 2λu) Vp

(18)

sujeto a W > λ_u V_p, y U = 0 en caso contrario, donde λ_u es el coeficiente de abstracción inicial del flujo base. De la Ec. 4:

V = W - U

(19)

Dada la precipitación anual y un conjunto de coeficientes iniciales de abstracción λ_s y λ_u y los potenciales W_p y V_p, las Ecs. 16-19 se utilizan para separar la precipitación anual en escorrentía superficial, flujo base y vaporización. Luego, la escorrentía se calcula mediante la Ec. 6, y los coeficientes de flujo base y escorrentía K_u y K_r se calculan utilizando las Ecs. 9 y 10, respectivamente.

4.  CALIBRACIÓN DEL MODELO

En ausencia de datos, los coeficientes de abstracción iniciales y los potenciales se estiman a partir de experiencias pasadas en entornos climáticos similares. Cuando hay datos disponibles, los parámetros del modelo pueden ser calibrados. Para λ = 0, Z_p se resuelve a partir de la Ec. 14:

X (X - Y) Zp = ___________               Y

(20)

Para λ > 0, Z_p se resuelve a partir de la Ec. 13:

X + [1/(2λ)] {(1 - 2λ) Y - [(1 - 2λ)2 Y 2 + 4λ (1 - λ) X Y]1/2} Zp = ________________________________________________________                                                   λ

(21)

Para calibrar los parámetros del modelo basados ​​en datos X-Y, se sugiere el siguiente procedimiento recursivo:

1. Establecer λ = 0 y Δλ = 0.01.

2. Utilizar la Ec. 20 o la Ec. 21 para calcular una Z_p para cada par X - Y, es decir, una matriz de Z_p.

3. Calcular la media, la desviación estándar y el coeficiente de variación de la matriz Z_p.

4. Detener el cálculo cuando el coeficiente de variación de la matriz Z_p haya alcanzado un mínimo; de lo contrario, aumentar λ un valor Δλ y volver al paso 2.

El λ calibrado es aquél para el cual el coeficiente de variación de la matriz Z_p es mínimo. El Z_p calibrado es la media de la matriz Z_p correspondiente al λ calibrado.

Este procedimiento se aplicó a los datos de L'vovich (1979), y los resultados de la calibración se muestran en las Tablas 1 y 2. Sobre la base de esta aplicación inicial, se sugiere una clasificación tentativa de rangos de parámetros: coeficiente de abstracción inicial λ (adimensional): bajo (0 < λ ≤ 0.1), promedio (0.1 < λ ≤ 0.3), alto (0.3 < λ ≤ 0.5), y muy alto (0.5 < λ ≤ 1); potencial Z_p (mm): bajo (0 ≤ Z_p ≤ 1000), promedio (1000 < Z_p ≤ 3000), alto (3000 < Z_p ≤ 5000), y muy alto (Z_p > 5000).

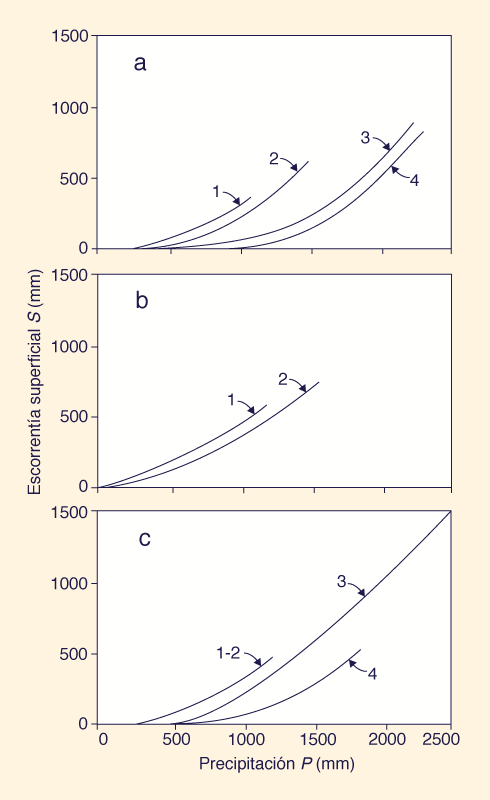
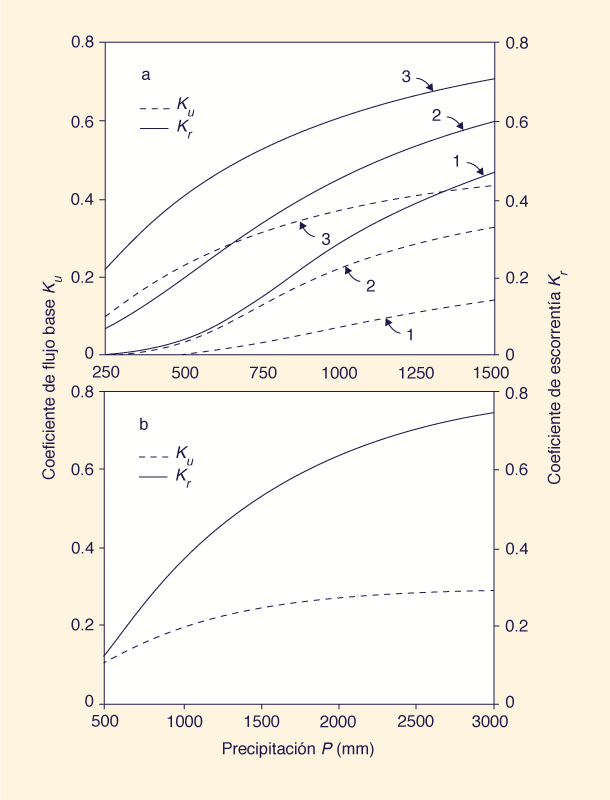
La Tabla 1 muestra los valores calibrados del coeficiente de abstracción inicial de la escorrentía superficial λ_s y potencial de humedad W_p para nueve conjuntos de datos P - S incluidos por L'vovich (1979) (Fig. 3). El análisis de la Tabla 1 conduce a las siguientes conclusiones:

1. Las llanuras árticas-subárticas y los bosques subárticos en Canadá tienen λ_s, = 0, y W_p de bajo a medio (889-1578 mm). El suelo casi congelado produce una respuesta inmediata de escorrentía superficial, en relación con la cantidad de precipitación.

2. Los bosques de coníferas de montaña en áfrica y los prados de montaña, estepas y sabanas en América del Sur tienen λ_s bajos (0.02-0.06), y W_p medios (1789-2164 mm).

3. Las sabanas en áfrica y América del Sur tienen valores medios de λ_s (0.18-0.22), y medios (bordeando los altos) de W_p (2627-2944 mm).

4. Los bosques y matorrales esclerófilos perennes en áfrica y los bosques siempre verdes húmedos en las montañas de América del Sur tienen valores medios a altos de λ_s (0.23-0.31), y valores medios de W_p (1326-1517 mm).

5. Los bosques húmedos perennifolios de áfrica tienen λ_s muy altos (0.54) y W_p medios (1970 mm). La abstracción inicial muy alta produce una respuesta de escorrentía superficial lenta.

Fig. 3  Relaciones precipitación-escorrentía superficial para regiones biogeográficas seleccionadas: (a) áfrica, (b) Canadá, y (c) América del Sur (Ver Tabla 1 para una explicación de los números de las curvas).

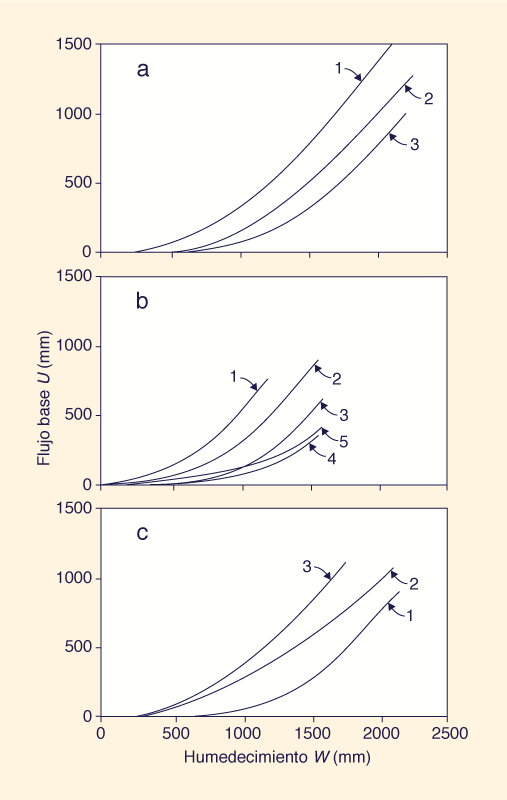
La Tabla 2 muestra los valores calibrados del coeficiente de abstracción inicial de flujo base λ_u y el potencial de vaporización V_p para 11 conjuntos de datos W - U incluidos por L'vovich (1979) (Fig. 4). El análisis de esta tabla conduce a las siguientes conclusiones:

1. Los bosques húmedos del sureste de América del Norte tienen λ_u = 0 y un V_p muy alto (6110 mm). Esto produce una respuesta de flujo base inmediata, en relación con la cantidad de humedad. Sin embargo, esto es atenuado por el valor muy alto del potencial de vaporización.

2. Los bosques subárticos y las estepas templadas de América del Norte tienen un λ_u bajo (0,09-0,10), mientras que V_p es bajo para los bosques subárticos (796 mm) y alto para las estepas templadas (4246 mm).

3. Los bosques mixtos con clima continental moderado en América del Norte y los bosques siempreverdes húmedos en las montañas de América del Sur tienen λ_u de bajo a medio (0.10-0.13) y V_p medio (1294-1856 mm).

4. Las llanuras y estepas boscosas en América del Norte y las praderas de alta montaña en América del Sur tienen un λ_u medio (0.19-0.25), mientras que V_p es bajo para las praderas de alta montaña (977 mm) y medio para las llanuras y estepas boscosas (2047 mm).

5. Los bosques de coníferas de montaña, los bosques y matorrales esclerófilos perennifolios y los paisajes montañosos en áfrica y las sabanas en América del Sur tienen un λ_u alto (0.35-0.48), con un V_p bajo a medio (903-1797 mm).

Fig. 4  Relaciones humedad-flujo base para regiones biogeográficas seleccionadas: (a) áfrica, (b) Canadá, y (c) América del Sur. (Consulte la Tabla 2 para obtener una explicación de los números de las curvas).

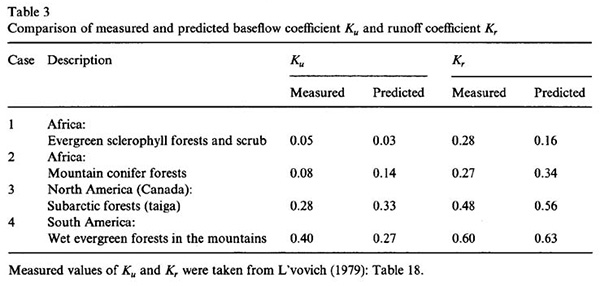
La Tabla 3 muestra una comparación de los coeficientes de flujo base y de escorrentía reportados por L'vovich (1979) y predichos por el modelo conceptual desarrollado aquí. Se ve que el modelo conceptual es razonablemente predictivo para una amplia gama de condiciones climáticas. La Figura 5 muestra los coeficientes de flujo base y de escorrentía calculados para regiones biogeográficas-climáticas seleccionadas que se muestran en la Tabla 3. Se ve que los coeficientes predichos por el modelo conceptual responden a variaciones en la entrada de precipitación.

Fig. 5  Coeficientes de caudal base y escorrentía en función de la precipitación media anual: (a) Casos 1, 2 y 3; (b) Caso 4. (Consulte la Tabla 3 para obtener una explicación de los números de las curvas).

El potencial de humedad W_p es un límite superior a la fracción de precipitación anual que puede retener una cuenca de captación determinada. Es probable que una cuenca de captación típica presente varias áreas, cada una con un potencial de humedad W_pi que cubre un área parcial A_i. Un potencial de humedad ponderado espacialmente para toda la cuenca es el siguiente:

∑ (Wpi Ai ) Wp = ___________               ∑ Ai

(22)

El potencial de vaporización V_p es un límite superior a la fracción de humedad anual que puede evaporarse de una cuenca de captación determinada. Es probable que una cuenca de captación típica tenga tres tipos distintos de superficies: (1) superficies con vegetación, con un potencial de evapotranspiración T_pv que cubre un área parcial A_v; (2) superficies sin vegetación, con un potencial de evaporación E_pn que cubre un área parcial A_n; (3) superficies de agua libre, con un potencial de evaporación E_pw que cubre un área parcial A_w. Un potencial de vaporización ponderado espacialmente para toda la cuenca es la siguiente:

Tpv Av + Epn An + Epw Aw Vp = ___________________________                      Av + An + Aw

(23)

5.  RESUMEN

Se formula un modelo conceptual del balance hídrico de una cuenca. El modelo se basa en la separación secuencial de la precipitación anual en escorrentía superficial y humedad, y la humedad en flujo base y vaporización. La separación se basa en una relación proporcional que vincula las tres variables involucradas en cada paso. La forma genérica de la relación proporcional es: (X - λZ_p - Y)/[(1 - λ) Z_p] = Y/(X - λZ_p), en la cual X es la variable independiente, Y es la variable dependiente, λ es el coeficiente de abstracción inicial, y Z_p es el valor potencial de la diferencia Z = X - Y.

Dado un conjunto de parámetros del modelo, el modelo puede separar la precipitación anual en sus tres componentes principales: escorrentía superficial, flujo base y vaporización. Además, los coeficientes de caudal base y escorrentía se caracterizan en función del clima. El modelo se puede utilizar para estimar el rendimiento anual de agua en todo el espectro climático. Una aplicación inicial del modelo a los datos de captación de L'vovich (1979) proporcionó resultados alentadores. Se necesita investigación adicional para determinar los coeficientes y potenciales de abstracción iniciales para una amplia gama de regiones biogeográficas y entornos climáticos asociados.

AGRADECIMIENTOS

El presente estudio se realizó en la primavera de 1994, durante la visita de A. V. Shetty a la Universidad Estatal de San Diego, con licencia del Centro Regional Hard Rock, Instituto Nacional de Hidrología, Belgaum, Karnataka, India. Su licencia fue financiada por el Programa de las Naciones Unidas para el Desarrollo.

BIBLIOGRAFíA

Crawford, N. H. y R. K. Linsley. 1966. Digital simulation in hydrology: the Stanford watershed model IV. Stanford Univ. Dep. Civ. Eng. Tech. Rep. 39.

Hamon, W.R. 1963. Computation of direct runoff amounts from storm rainfall. Int. Assoc. Sci. Hydrol. Publ., 63: 52-62.

Lee, R. 1970. Theoretical estimates versus forest venter yield. Water Resour. Res., 6(5): 1327-1334.

L'vovich, M. I. 1979. World water resources and their future. Original in Russian. English translation, American Geophysical Union, Washington, DC.

Sutcliffe, J. V. y W. R. Rangeley. 1960. Variability of annual river flow related to rainfall records. Int. Assoc. Sci. Hydrol. Publ., 76: 182-192.

U.S. Department of Agriculture Soil Conservation Service (USDA SCS). 1985. National Engineering Handbook, Section 4: Hydrology. SCS, Washington, DC.

Woodruff, J. F. y J. D. Hewlett. 1970. Predicting and mapping the average hydrologic response for the Eastern United States. Water Resour. Res., 6(5): 1312-1326.