Número de Froude
para la iniciación del movimiento
calculado en línea


Victor M. Ponce and Janaina Da Silva


19 Abril 2018


Resumen. El criterio clásico de Shields de la ingeniería de sedimentación se expresa en términos del número de Froude y la velocidad media asociada para iniciar el movimiento en un canal de lecho móvil. Para resolver el problema con precisión, se implementa un algoritmo iterativo en la calculadora EN LINEA SHIELDS VELOCIDAD, accesible en línea en http://ponce.sdsu.edu/enlineashieldsvelocidad.php

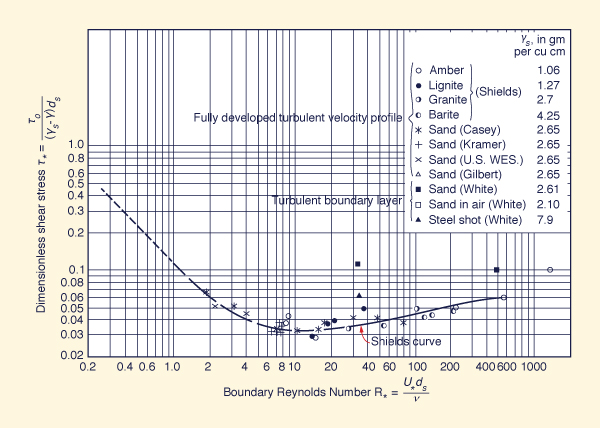
1.  INTRODUCCIÓN

Shields (Sociedad Estadounidense de Ingenieros Civiles, 1975; p. 96) fue pionero en estudiar la iniciación del movimiento en el flujo en un canal de lecho móvil. La curva de Shields es el umbral en el que las partículas del material del lecho comienzan a moverse (Fig. 1). Este umbral es importante en el diseño de canales para asegurar el movimiento de sedimentos y evitar obstrucciones. En este artículo expresamos el criterio de Shields en términos del número de Froude y la velocidad media asociada requerida para iniciar el movimiento en un canal de lecho móvil. Para completar la experiencia, desarrollamos un algoritmo iterativo para calcular estos valores en línea.

2.  EL CRITERIO DE SHIELDS

El criterio de Shields para la iniciación del movimiento relaciona el esfuerzo cortante adimensional τ* con el número de Reynolds límite R* como se muestra en la Figura 1. La curva sólida separa el movimiento por encima de la curva, de la ausencia de movimiento por debajo de la curva. El criterio de Shields es el siguiente:

               τo
τ* = ____________  ≥  τ*c
          (γs - γ) ds 		(1)

en la cual τo = esfuerzo cortante en el fondo, γs = peso específico de las partículas de sedimento, γ = peso específico del agua, ds = diámetro de las partículas, y τ*c = esfuerzo cortante crítico adimensional.

groundwater balance

Fig. 1 Curva de Shields para la iniciación del movimiento (Sociedad Estadounidense de Ingenieros Civiles, 1975).

3.  EL CRITERIO DE FROUDE

El número de Froude es:

             V
F = __________
         (g D )1/2 		(2)

en la cual g = aceleración gravitacional, y D = profundidad hidráulica.

La fórmula de fricción cuadrática en flujo en canal abierto es la siguiente (Ponce, 2014):

τo = ρ f V 2 (3)

en la cual ρ = densidad de masa, f = factor de fricción, igual a 1/8 del factor de fricción de Darcy-Weisbach fD, and V = velocidad media.

Reemplazando las Ecs. 2 y 3 en 1:

             f D F 2
___________________  ≥  τ*c
      [ (γs /γ ) - 1 ] ds 		(4)

En la mayoría de los casos de interés práctico, la relación γs /γ = 2.65. En este caso, el número de Froude para la iniciación del movimiento es el siguiente:

              1.65 τ*c (ds / D )
F  ≥  { __________________ } 1/2
                          f 		(5)

Como primera aproximación, la curva de Shields sugiere un valor constante del esfuerzo cortante adimensional crítico τ*c = 0.04, aplicable a una amplia gama de números de Reynolds de contorno (Fig. 1). Por lo tanto, la Ec. 5 se reduce a lo siguiente:

              0.066 (ds / D )
F  ≥  { ________________ } 1/2
                         f 		(6)

El factor de fricción varía normalmente en el rango 0.002 ≤ f ≤ 0.005, que corresponde a los factores de fricción de Darcy-Weisbach 0.016 ≤ fD ≤ 0.040. Para ilustrar, asumimos un valor medio f = 0.0035. Por tanto, el criterio de Froude aplicable es el siguiente:

F  ≥  4.342 (ds / D )1/2 (7)

Para un diámetro de partícula dado, en relación con la profundidad hidráulica, la Ec. 7 establece el número de Froude que debe superarse para asegurar el inicio del movimiento. Por ejemplo, para ds = 0.4 mm y profundidad hidráulica D = 1 m, es decir, (ds / D ) = 0.0004, Ec. 7 se reduce a lo siguiente:

F  ≥  0.087 (8)

Combinando las Ecs. 2 y 6, la velocidad media relacionada es:

              0.066 g ds
V  ≥  [ _____________ ] 1/2
                      f 		(9)

Por lo tanto: V = 0.27 m/s.

4.   APLICACIÓN CON EL COEFICIENTE DE MANNING

La relación entre el factor de fricción f y la n de Manning es la siguiente: (Ponce, 2014):

            g n 2
f = ___________
         k 2 R 1/3 		(10)

en la cual g = aceleración gravitacional, n = n de Manning, R = radio hidráulico y k = una constante igual a 1 en unidades SI y 1,486 en unidades habituales de EE.UU.

Para un canal hidráulicamente ancho: R ≅ D. Reemplazando la Ec. 10 en la Ec. 6, la expresión del número de Froude en unidades SI es la siguiente:

           0.082 D 1/6 (ds / D )1/2
F  ≥  _______________________
                          n 		(11)

Por ejemplo, dados D = 1 m, ds = 0.4 mm = 0.0004 m, y n = 0.019:

F  ≥  0.086 (12)

En las unidades habituales de EE.UU., la expresión del número de Froude es el siguiente:

            0.067 D 1/6 (ds / D )1/2
F  ≥  ________________________
                          n 		(13)

en el cual D y ds se expresan en pies.

Por ejemplo, dado: D = 3.28 pies, ds = 0.4 mm = 0.001312 pies, y n = 0.019:

F  ≥  0.086 (14)

5.  ALGORITMO ITERATIVO

Se puede obtener un cálculo más preciso del número de Froude y la velocidad media relacionada utilizando (en la Ecuación 5) un esfuerzo cortante crítico adimensional obtenido de la curva de Shields, en lugar del valor constante aproximado de 0,04. Este procedimiento, sin embargo, requiere una iteración, lo cual sugiere el siguiente algoritmo.

Algoritmo utilizado en EN LINEA SHIELDS VELOCIDAD

  1. Asumir R*

  2. Usar la Fig. 1 para encontrar τ*c

  3. Utilizar la Ec. 1, calcular τo

  4. Utilizar la Ec. 3 para calcular la velocidad de corte: U* = (τo /ρ)1/2

  5. Calcular el nuevo valor de R* = (U* ds / ν), en la cual ν = viscosidad cinemática, una función de la temperatura.

  6. Detenerse si el nuevo valor de R* está cerca del valor asumido en el Paso 1 (dentro de una pequeña tolerancia), y usar el último valor de τ*c (obtenido en el Paso 2) en la Ec. 5;

  7. De lo contrario, regresar al Paso 1 y usar el nuevo valor de R* (calculado en el Paso 5) como el valor asumido y proseguir con la iteración.



 Ejemplo.

Dados los siguientes datos:   Diámetro de partícula ds = 0.4 mm, profundidad hidráulica D = 1 m, factor de fricción adimensional de Darcy-Weisbach f = 0.0035, y temperatura del agua T = 20°C. Calcular el número de Froude y la velocidad media relacionada en el umbral de iniciación del movimiento usando EN LINEA SHIELDS VELOCIDAD.

calculator image 

CÁLCULO EN LÍNEA. Utilizando el algoritmo iterativo incorporado en EN LINEA SHIELDS VELOCIDAD, el número de Froude es F = 0.081 y la velocidad media V = 0.25 m/s. Notese que estos resultados son más precisos que los obtenidos en el cálculo directo utilizando las Ecs. 6 y 9.

6.  RESUMEN

El criterio clásico de Shields se expresa en términos del número de Froude y la velocidad media relacionada, requerida para iniciar el movimiento en un canal de lecho movil. Para resolver el problema con una mayor precisión, se implementa un algoritmo iterativo en la calculadora EN LINEA SHIELDS VELOCIDAD, accesible en http://ponce.sdsu.edu/enlineashieldsvelocidad.php

BIBLIOGRAFÍA

American Society of Civil Engineers. 1975. Sedimentation Engineering. ASCE Manuals and Reports on Engineering Practice No. 54.

Ponce, V. M. 2014. Fundamentos de la hidráulica de canales. texto en linea.

221124