skip to main content

RESUMEN Los perfiles de la superficie del agua en el flujo gradualmente variado se expresan en términos de la pendiente crítica Sc. De esta forma, se demuestra que el gradiente de profundidad de flujo dy/dx está estrictamente limitado a valores fuera del rango comprendido entre Sc y So, en el cual So es la pendiente de fondo. Este enfoque mejora y completa la definición de rangos de gradiente de profundidad de flujo en el análisis de perfiles de la superficie del agua. Se presentan varias calculadoras en línea para complementar la experiencia.

1.  INTRODUCCIÓN

Los cálculos del flujo gradualmente variado (FGV) son parte de la práctica común de la ingeniería hidráulica. La ecuación de FGV describe un flujo gradualmente variado en canales abiertos (Chow 1959; Henderson 1966). La ecuación convencional se expresa en términos de la pendiente de fondo S_o, la pendiente de fricción S_f, y el número de Froude F. En este artículo, la ecuación se expresa alternativamente en términos de la pendiente de fondo S_o, la pendiente crítica S_c, y el número de Froude F. El análisis de esta ecuación revela que el gradiente de profundidad de flujo dy/dx está estrictamente limitado a valores fuera del rango comprendido entre S_o y S_c. Este enfoque mejora y completa la definición de rangos de gradiente de profundidad de flujo en el análisis de perfiles de la superficie del agua.

2.  ECUACIÓN DEL FLUJO GRADUALMENTE VARIADO

La ecuación del flujo gradualmente variado es (Chow 1959, p. 220; Henderson 1966, p. 130):

dy                    So - Sf ___  =  ____________________  dx          1 - [(Q 2 T ) / (g A 3)] (1)

en la cual y = profundidad de flujo, x = distancia a lo largo del canal, dy/dx = gradiente de la profundidad de flujo, Q = caudal, T = ancho superior, A = área de flujo, y g = aceleración gravitacional. Esta ecuación es válida para pendientes de fondo pequeñas (S_o < 0.1), lo cual suele ser el caso. La pendiente de fricción en términos del coeficiente C de Chezy es (Chow 1959):

Q 2 Sf  =  __________            C 2 A 2 R (2)

en la cual R = A/P = radio hidráulico, y P = perímetro mojado.

El número de Froude en términos del caudal es (Chow 1959):

Q 2 T F 2  =  _______               g A 3 (3)

La combinación de las Ecs. 2 y 3 conduce a lo siguiente:

Sf  =  (P / T ) (g / C 2) F 2 (4)

En flujo crítico normal, F = 1, y la pendiente de fricción en el estado crítico, es decir, la pendiente crítica, es:

Sc  = (Pc / Tc ) (g / C 2) (5)

Combinando las Ecs. 1, 4 y 5:

dy          So - Sc F 2 ___  =  ___________  dx             1 - F 2 (6) lo cual es estrictamente válido para la siguiente condición:  P /T = Pc /Tc . Esta última condición generalmente se cumple en un canal hidráulicamente ancho, para el cual T es asintóticamente igual a P. Para facilitar la expresión, el gradiente de profundidad de flujo se renombra aqui como Sy = dy/dx. Resolviendo la Ecuación 6 para el número de Froude:                So - Sy F 2  =   _________                Sc - Sy (7) Dado que F 2 > 0, el gradiente de profundidad de flujo debe satisfacer las siguientes desigualdades: So ≥ Sy ≤ Sc (8) So ≤ Sy ≥ Sc (9) lo que limita efectivamente el gradiente de profundidad de flujo a valores fuera del rango comprendido entre So y Sc. Además, la Ecuación 6 se puede expresar alternativamente de la siguiente manera:  Sy          ( So / Sc ) - F 2 ___  =  ______________  Sc                1 - F 2 (10) La Ecuación 10 es la ecuación de flujo gradualmente variado en términos de la pendiente de fondo So, la pendiente crítica Sc, y el número de Froude F. La pendiente de fondo puede ser positiva (fuerte, crítica o suave), cero (horizontal) o negativa (adversa). La pendiente crítica (Ecuación 5) y el número de Froude al cuadrado (Ecuación 3) son siempre positivos. 3.  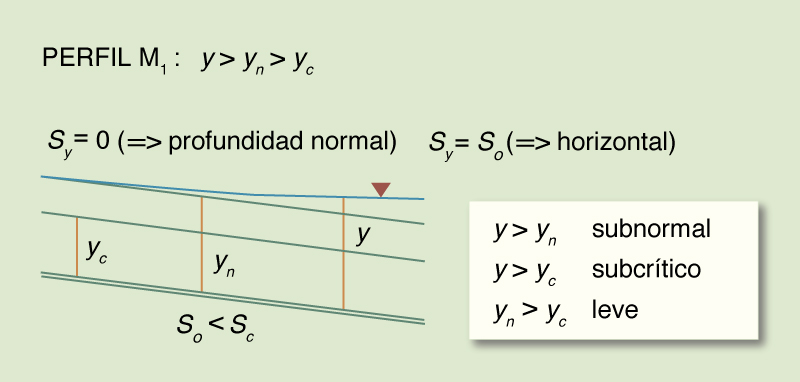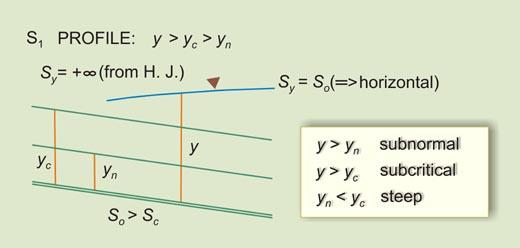CLASIFICACIÓN DE LOS PERFILES DE AGUA SUPERFICIAL La Ecuación 10 se usa para desarrollar una clasificación de los perfiles de agua superficial basada únicamente en los tres parámetros adimensionales: Sy/Sc, So/Sc, y F. Aclarando, el flujo subcrítico se define como aquél para el cual la profundidad de flujo es mayor que la profundidad crítica (F 2 < 1) (Chow 1959; Henderson 1966). Paralelamente a esta ampliamente aceptada definición, el flujo subnormal se define como aquél para el cual la profundidad de flujo es mayor que la profundidad normal [F 2 < So /Sc ]. El flujo supernormal se define como aquél para el cual la profundidad de flujo es menor que la profundidad normal [F 2 > So /Sc ] (USDA SCS 1971). La Tabla 1 muestra las cuatro (4) clases de perfiles de la superficie del agua y los doce (12) perfiles posibles. Tabla 1.  Clases y tipos posibles de perfiles de superficie del agua. CLASE 1:  SUBCRÍTICA/SUBNORMAL Fuerte:  S1 Crítica:  C1 Suave:  M1 CLASE 2A:  SUPERCRÍTICA/SUBNORMAL Fuerte:  S2 CLASE 2B:  SUBCRÍTICO/SUPERNORMAL Suave:  M2 Horizontal:  H2 Adversa:  A2 CLASE 3:  SUPERCRÍTICO/SUPERNORMAL Fuerte:  S3 Crítica:  C3 Suave:  M3 Horizontal:  H3 Adversa:  A3 En la Tabla 2 se muestra un resumen de los doce posibles perfiles de superficie del agua. La clasificación se deriva directamente de la ecuación de gobierno (Ecuación 10). Se ve que la clase general de perfil (Clase 1, 2A, 2B o 3) determina el signo de Sy/Sc (Columna 2) y, por lo tanto, la clasificación del perfil en curva de remanso, o de abatimiento (Columna 3). Asimismo, la clase general de perfil determina el rango factible de So/Sc (Columna 4) y, por tanto, la existencia de tipos de perfiles específicos (Fuerte, Crítico, Suave, Horizontal, o Adverso) dentro de cada tipo general. Téngase en cuenta que no todas las combinaciones de Sy/Sc y So/Sc son factibles. A diferencia de la descripción disponible en las referencias estándar (Chow 1959; Henderson 1966), los rangos de gradiente de profundidad de flujo (Tabla 2, Columnas 7 y 8) están ahora completos para los doce perfiles de superficie del agua. Está claro que el gradiente de profundidad de flujo Sy está fuera del rango comprendido entre Sc y So. 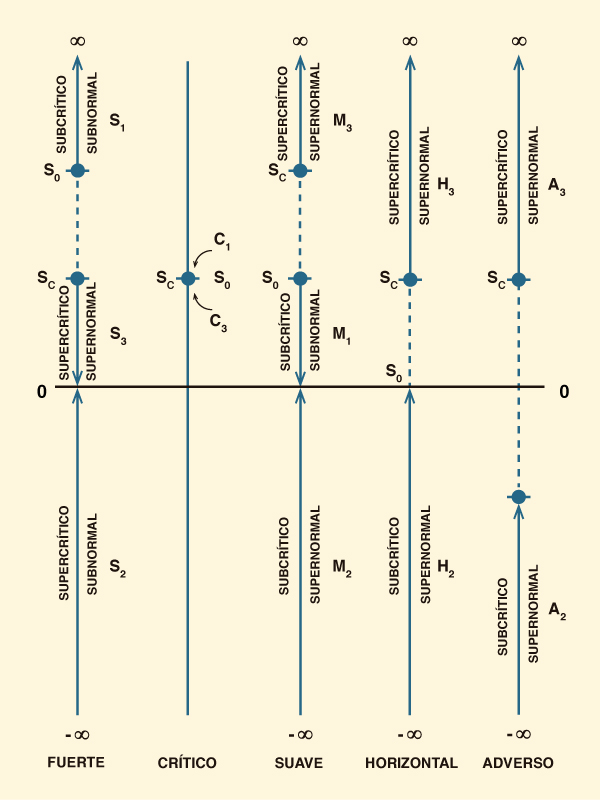La Figura 1 muestra una representación gráfica de los rangos de gradiente de profundidad del flujo en los perfiles de la superficie del agua. La flecha muestra la dirección del cálculo. Por ejemplo, el gradiente de profundidad para el perfil S3 (supercrítico/supernormal) disminuye de Sc (un valor positivo finito) a 0 (flujo asintótico al flujo normal). Asimismo, el gradiente de profundidad para los perfiles C1 (subcrítico/subnormal) y C3 (supercrítico/supernormal) es constante e igual a So = Sc. Las calculadoras en línea del perfil de la superficie del agua se muestran en la Tabla 2. Tabla 2.  Clasificación de los perfiles de agua superficial. [Haga clic en cualquier tipo de perfil en la Col. 9 para accesar la calculadora en línea.] No. (1) Sy /Sc (2) Perfil (3) So /Sc (4) Pendiente (5) Relaciones de profundidad (6) Sy varía Tipo de perfil (9) De (7) A (8) 1.  FLUJO SUBCRÍTICO/SUBNORMAL 1 :   1 > F 2 < So / Sc 1 Positivo Remanso > 1 Empinado y > yc > yn So ∞ S1 2 Positivo Remanso = 1 Crítico y > yc = yn So = Sc So = Sc C1 3 Positivo Remanso < 1; > 0 Suave y > yn = yc So 0 M1 2A.  FLUJO SUPERCRÍTICO/SUBNORMAL 2 :   1 < F 2 < So / Sc 4 Negativo Abatimiento > 1 Empinado yc > y > yn - ∞ 0 S2 2B.  FLUJO SUBCRÍTICO/SUPERNORMAL 3 :   1 > F 2 > So / Sc 5 Negativo Abatimiento < 1; > 0 Suave yn > y > yc - ∞ 0 M2 6 Negativo Abatimiento = 0 Horizontal y > yc ; yn → ∞ - ∞ So = 0 H2 7 Negativo Abatimiento < 0 Adverso y > yc ; yn → ∞ - ∞ So < 0 A2 3.  FLUJO SUPERCRÍTICO/SUPERNORMAL 4 :   1 < F 2 > So / Sc 8 Positivo Remanso > 1 Empinado yc > yn > y Sc 0 S3 9 Positivo Remanso = 1 Crítico yc = yn > y So = Sc So = Sc C3 10 Positivo Remanso < 1; > 0 Suave yn > yc > y Sc ∞ M3 11 Positivo Remanso = 0 Horizontal yc > y ; yn → ∞ Sc ∞ H3 12 Positivo Remanso < 0 Adverso yc > y ; yn → ∞ Sc ∞ A3 1 Dado que So /Sc > F 2 > 0, no son posibles perfiles horizontales o adversos en flujo subcrítico/subnormal. 2 Dado que So /Sc > 1, no son posibles perfiles críticos, leves, horizontales o adversos en flujo supercrítico/subnormal. 3 Dado que So /Sc < 1, no son posibles perfiles empinados o críticos en flujo subcrítico/supernormal. 4 Dado que So /Sc no está limitado, los cinco perfiles son posibles en flujo supercrítico/supernormal. Figura 1.   Representación gráfica de los rangos de gradiente de profundidad de flujo en los perfiles de superficie del agua. 4.  RESUMEN La ecuación de flujo gradualmente variado se expresa en términos de la pendiente crítica Sc. De esta forma, se demuestra que el gradiente de profundidad de flujo dy/dx está estrictamente limitado a valores fuera del rango comprendido entre So y Sc. Esto completa la definición de rangos de gradiente de profundidad para todos los perfiles de la superficie del agua. Por ejemplo, para el perfil S3, el gradiente de profundidad de flujo disminuye de Sc (un valor positivo finito) a 0 (asintótico a la profundidad normal). Asimismo, el gradiente de profundidad de flujo para todos los perfiles C1 y C3 es constante e igual a So = Sc. La Tanla 3 muestra un resumen de los perfiles de la superficie del agua. Se presentan calculadoras en línea para completar la experiencia. Tabla 3.  Resumen de los perfiles de la superficie del agua. [Haga clic en cualquier imagen para desplegar] Familia Caracteristicas Regla So > Sc So = Sc So < Sc So = 0 So < 0 1 Retardado (Remanso) 1 > F 2 < So / Sc S1 C1 M1 - - 2A Acelerado (Abatimiento) 1 < F 2 < So / Sc S2 - - - - 2B Acelerado (Abatimiento) 1 > F 2 > So / Sc - - M2 H2 A2 3 Retardado (Remanso) 1 < F 2 > So / Sc S3 C3 M3 H3 A3 BIBLIOGRAFÍA Chow, V. T. (1959). Open-channel hydraulics. McGraw-Hill, New York. Henderson, F. M. (1966). Open channel flow. MacMillan, New York. USDA Soil Conservation Service. (1971). Classification system for varied flow in prismatic channels. Technical Release No. 47 (TR-47), Washington, D.C.

230622