Upper Paraguay river at Porto Murtinho, Mato Grosso do Sul, Brazil, featuring a flood hydrograph lasting one year (the maximum possible), clearly the quintessential kinematic flood wave.


THE PONCE-SIMONS NUMBER


Victor M. Ponce

Professor Emeritus of Civil and Environmental Engineering

San Diego State University, San Diego, California


January 29, 2024

ABSTRACT.  The three diffusivities relevant in fluid mechanics and open-channel flow (molecular, hydraulic, and spectral), are appropriately defined and explained. This article focuses on the Ponce-Simons number, properly the ratio of hydraulic and spectral diffusivities, while being affected with the factor 2π. This dimensionless number characterizes the spatial scale and associated properties of surface disturbances in unsteady open-channel flow.

1.  INTRODUCTION

In hydraulic engineering, viscosity, or its synonym, diffusivity, is a fundamental fluid property. Diffusivity is the first moment of the flow velocity. Therefore, the units of diffusivity are (L/T)L, or its equivalent expression L2/T. The equality ν = 1 m2/sec describes the mathematical certainty that a given disturbance will diffuse at the rate of ν = 1 m2/sec. In fluid mechanics, diffusivity relates to the process of diffusion; in engineering hydrology, to flood wave attenuation, or dissipation. In hydraulic mathematical modeling, diffusivity is described by the second-order term of a differential equation (Table 1).

Table 1.  Comparison of velocities and diffusivities in open-channel flow.
Property Symbol Units Process Order
VelocityuL/T Convection, advectionFirst
Diffusivity ν L2/T Diffusion, dissipationSecond

The fluid properties listed in Table 1 describe the flow up to second order. In this article, we focus on the Ponce-Simons number, a ratio of diffusivities which characterizes the spatial scale of the wave phenomena. Increased understanding of this dimensionless number significantly enhances the comprehension of wave phenomena in unsteady open-channel flow.

2.  DIFFUSIVITIES IN OPEN-CHANNEL FLOW

Three diffusivities are recognized in open-channel flow:

  1. Molecular diffusivity,

  2. Hydraulic diffusivity, and

  3. Spectral diffusivity.

In fluid mechanics, the molecular diffusivity νm is commonly referred to as kinematic viscosity ν, a measure of the fluid's internal resistance to flow at the molecular level. In open-channel flow, the hydraulic diffusivity νh is expressed in terms of the unit-width discharge and bottom slope. In unsteady open-channel flow, the spectral diffusivity νs is defined in terms of the wavelength of the sinusoidal perturbation to the steady flow. These propositions are further explained in Box A.

Box A.  Diffusivities in open-channel flow.

  1. Newton's law of viscosity is: τ /ρ = ν (∂u/∂s), in which τ = shear stress, ρ = mass density of the fluid, ν = kinematic viscosity of the fluid (molecular diffusivity) and (∂u/∂s) = velocity gradient in the direction s perpendicular to the direction of τ. For our purpose:

    τ /ρ = νm (∂u/∂s)

    The molecular diffusivity may be expressed as νm = u (Lm /2), in which Lm = (2νm /u)  is a characteristic molecular length (Chow, 1959).

  2. The hydraulic diffusivity is defined as νh = u (Lo /2), in which Lo = (do /So) is a characteristic hydraulic length, defined as the distance measured along the channel wherein the flow drops a head (i.e., an elevation) equal to its equilibrium depth (Hayami, 1951; Ponce and Simons, 1977).

  3. The spectral diffusivity νs is defined as νs = u (L /2), in which L = characteristic wavelength of the sinusoidal surface disturbance (Ponce, 1979).

    Note that all three diffusivities (molecular, hydraulic, and spectral) are defined in terms of their respective characteristic lengths: (1) molecular length Lm, (2) hydraulic length Lo, and (3) spectral wavelength L. Pointedly, we observe that the three diffusivities share a similar algebraic structure: A product of the convective velocity times one-half of the respective characteristic length.

3.  THE PONCE-SIMONS NUMBER

The three diffusivities identified in Box A give rise to only two independent dimensionless numbers (Ponce, 2023b):

  1. The ratio of hydraulic to molecular diffusivity, clearly a type of Reynolds number; and

  2. The ratio of hydraulic to spectral diffusivity, a type of Ponce-Simons number.

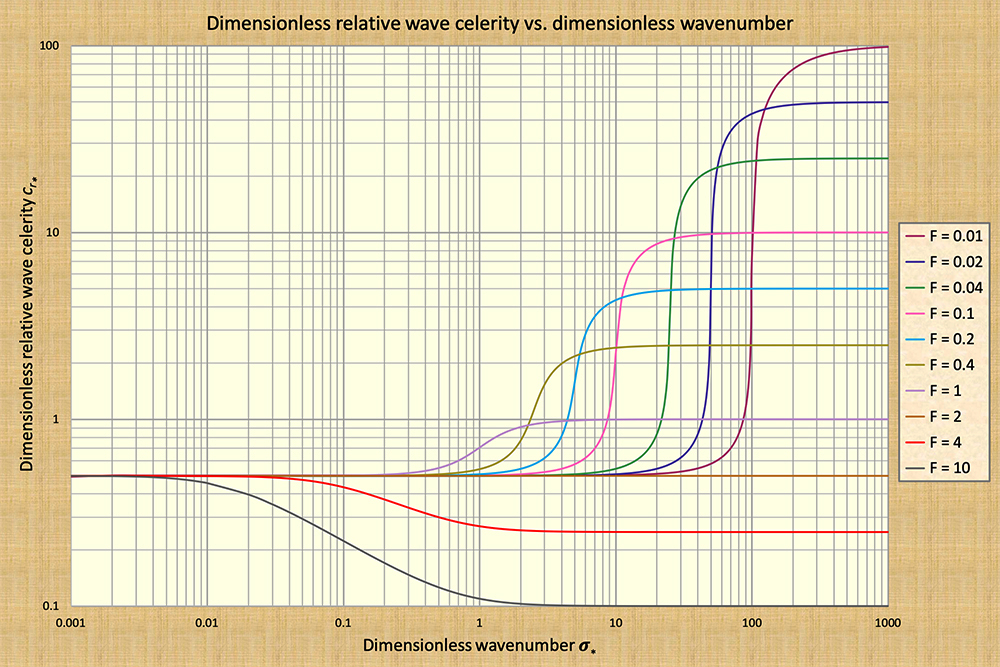
In their seminal work on shallow wave propagation, Ponce and Simons (1977) defined a dimensionless wavenumber as follows: σ* = (2π /L)Lo. It is observed that the Ponce-Simons number is indeed a surrogate for a ratio of diffusivities, since: σ* = (2π /L)Lo = 2π (νh /νs).

The Ponce-Simons dimensionless wavenumber σ* classifies the entire realm of unsteady flow disturbances into four spectral ranges (Fig. 1):

  1. Kinematic (extreme left),

  2. Diffusion (left-of-center),

  3. Mixed kinematic-dynamic (right-of-center), and

  4. Dynamic (extreme right).

The precise domains of these ranges have been examined by Ponce (2023a):

  • Kinematic flow: σ* < 0.001.

  • Diffusion flow: 0.001 ≤ σ* < 0.17.

  • Mixed kinematic-dynamic flow: 0.17 ≤ σ* < 1 to 100, depending on the Froude number (refer to Fig. 1).

  • Dynamic flow: σ* ≥ 10 to 1000, depending on the Froude number (refer to Fig. 1).

Ponce and Simons (1977)

Fig. 1   Dimensionless relative wave celerity cr* vs dimensionless wavenumber σ*.

The findings of Ponce and Simons (1977), depicted in Fig. 1, elucidate the behavior of all wave types in unsteady open-channel flow. These include both "long" waves, of a kinematic nature, towards the far left side of Fig. 1, and "short" waves, of a dynamic nature, towards the far right, both of which ostensibly feature constant celerity. Also included are the diffusion waves, in the left-of-center range and displaying properties that are shown to be quite practical, and the mixed kinematic-dynamic waves in the right-of-center range. The latter are, for the most part, impractical due to their extremely strong dissipative tendencies (Ponce, 2023a).

4.  SUMMARY

The three diffusivities relevant in fluid mechanics and open-channel flow [(1) molecular, (2) hydraulic, and (3) spectral)], are appropriately defined and explained. This article focuses on the Ponce-Simons number, properly the ratio of hydraulic and spectral diffusivities, while being affected with the factor 2π. This dimensionless number characterizes the spatial scale and associated properties of surface disturbances in unsteady open-channel flow.

REFERENCES

Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York, NY.

Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December, Extract.

Ponce, V. M. and D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering ASCE, 103(12), 1461-1476.

Ponce, V. M. 1979. On the classification of open channel flow regimes. Proceedings, Fourth National Hydrotechnical Conference, Vancouver, British Columbia, Canada.

Ponce, V. M. 2023a. When is the diffusion wave applicable? Online article.

Ponce, V. M. 2023b. Ths states of flow Online article.

240129