|
ONDAS CINEMÁTICO-DINÁMICAS MIXTAS DESBANCADAS
Profesor Emérito de Ingeniería Civil
Universidad Estatal de San Diego,
California
Introducción
En el modelamiento de ondas de inundación, a menudo la primera pregunta
que se presenta es la siguiente: ¿Qué tipo de onda debo utilizar? Al respecto, observamos
que las ondas cinemáticas y
difusivas están ya bien establecidas en la práctica. Por otro lado, reconocemos que las ondas
dinámicas de Lagrange no se prestan generalmente a aplicaciones de ondas
de inundación.
Durante los últimos cincuenta años, el enfoque que parece haber prevalecido en algunos
sectores es el siguiente: "Olvídémosnos de los distintos tipos de ondas; utilicemos la
solución completa de las ecuaciones de St. Venant en todas las aplicaciones y dejemos
que la computadora haga los cálculos". Observamos que la teoría y la práctica
han confirmado que este enfoque es generalmente fútil.
Nuestro objetivo es mostrar que el uso exclusivo de ondas mixtas es,
en el mejor de los casos, inútil, y en el peor, incorrecto, siendo muy probable
que lleve a pérdida de tiempo y recursos. En un esfuerzo por propiciar la claridad,
en la siguiente
sección enumeramos los diferentes tipos de ondas que se utilizan actualmente,
a la vez que detallamos su naturaleza y propiedades.
Tipos de ondas
En el flujo unidimensional no permanente en canales abiertos se utilizan generalmente
los siguientes tipos de ondas: (1) cinemática; (2) difusiva;
(3) mixta; y (4) dinámica. Las ondas cinemáticas excluyen los términos
de inercia y gradiente de presiones; las ondas difusivas excluyen sólo los términos
de inercia; las ondas mixtas no excluyen ningún
término, y las ondas dinámicas excluyen los términos de fricción y gravedad (Tabla 1).
Los términos excluidos no se consideran porque se asume que son demasiado pequeños
para afectar materialmente las propiedades de la onda en cuestión.
Propiedades de las ondas
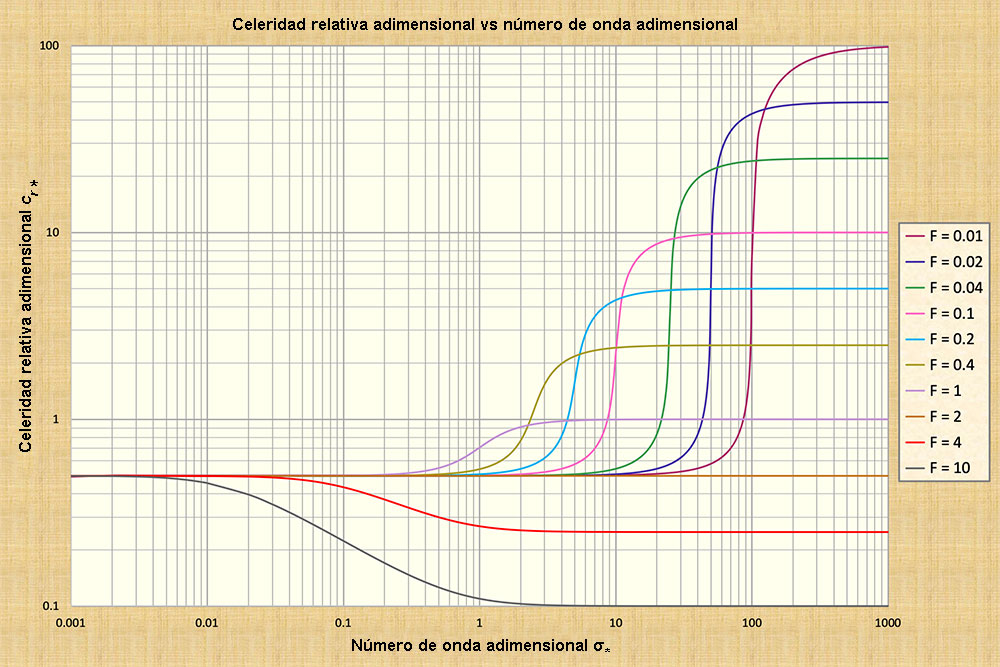
Ponce y Simons (1977) han examinado detalladamente las propiedades de los diversos tipos de ondas (Figs. 1 y 2).
Ellos utilizaron la teoría de la estabilidad lineal para determinar las funciones
de celeridad y atenuación para las siguientes ondas: (1) cinemáticas, (2) difusivas, (3) mixtas, y
Las ondas cinemáticas son las de Seddon (1900), mientras que las ondas dinámicas son las
de Lagrange (1788). Las ondas cinemático-dinámicas mixtas, a las que aquí referimos
simplemente como ondas mixtas, son aquéllas que se encuentran hacia
el centro-derecha del espectro del número de onda adimensional (Fig. 1). Estas ondas aparecieron en los modelos numéricos desarrollados a partir
de la década de 1970 para resolver las ecuaciones completas de St. Venant; véase,
por ejemplo, Fread (1985). Estos modelos han sido ampliamente denominados modelos
de "ondas dinámicas", aunque lo inapropiado del nombre
ha causado confusión con
las ondas dinámicas de Lagrange (1788), establecidas desde hace más de dos siglos.
Las ondas difusivas se encuentran a la derecha de las ondas cinemáticas y a la
izquierda de las ondas mixtas en el espectro del número de onda adimensional
(Fig. 1). A diferencia de las ondas cinemáticas, que presentan difusión cero,
las ondas difusivas tienen una cantidad de difusión pequeña pero medible.
Sin embargo, esta difusión es pequeña en comparación con la de las ondas mixtas
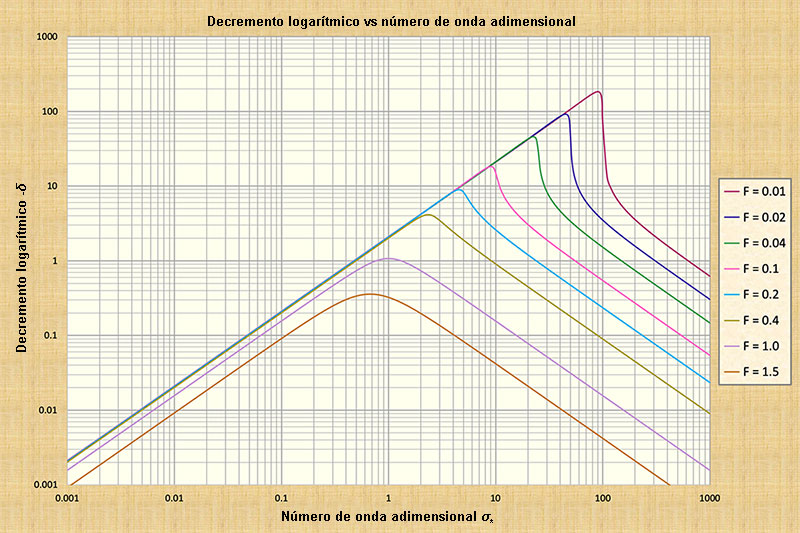
(Fig. 2). Observamos que la inclusión del término gradiente de presiones (Tabla 1)
es directamente responsable por la difusión.
La Figura 1 muestra que las ondas cinemáticas de Seddon, las cuales se encuentran hacia la izquierda
del espectro del número de onda adimensional, presentan una celeridad constante y, por
lo tanto, no son difusivas. Siguiendo el mismo razonamiento, las ondas dinámicas de Lagrange,
situadas hacia la derecha, tampoco son difusivas. Sin embargo, las ondas mixtas,
las cuales se encuentran hacia el centro-derecha y que muestran una celeridad altamente variable, son
fuertemente difusivas.
Ondas cinemáticas
De hecho, una onda cinemática puede considerarse como la onda de inundación veritas.
Ondas difusivas
A diferencia de las ondas cinemáticas, las ondas difusivas
están sujetas a una pequeña cantidad de difusión. Se encuentran
inmediatamente a la derecha de las ondas cinemáticas en el espectro
de números de onda adimensional, propiamente dentro
del rango 0,01 ≤ σ* ≤ 0,17 (Fig. 1)
Las ondas de inundación típicas se difusionan un tanto;
entonces, las ondas difusivas son un modelo apropiado
de propagación de ondas de inundación. Complementan
muy bien a las ondas cinemáticas, aunque encuentran su
mejor aplicación en los casos en que la difusión de las
ondas es apreciable, forzando la necesidad de su cálculo.
Sin embargo, surge el siguiente problema:
Los modelos numéricos de ondas cinemáticas
convencionales muestran de hecho cierta cantidad de difusión.
La cuestión de cómo manejar mejor la difusión numérica ha
sido resuelta por Cunge (1969), quien propuso una coincidencia
de la difusión numérica del esquema mismo con la difusión física
de la ecuación de la onda cinemática con difusión,
es decir, la ecuación de la onda difusiva. Este desarrollo
llevó al método Muskingum-Cunge de enrutamiento
de inundaciones, una alternativa con base física al
clásico método Muskingum (Ponce, 2014).
Ondas dinámicas
Las ondas dinámicas clásicas son las de Lagrange (1788). Más recientemente,
Fread (1985) y otros se han referido a las ondas cinemático-dinámicas mixtas como
ondas "dinámicas", mientras que aquí nos referimos a ellas simplemente como
ondas "mixtas". La confusión semántica es realmente desafortunada. En un intento
de contribuir a solucionar el problema, aquí utilizamos el adjetivo "dinámica"
para referirnos únicamente a las ondas de Lagrange.
Las ondas dinámicas presentan una celeridad de onda constante para el
número de onda adimensional σ* ≥ 100 para la mayoría de los números de Froude,
y σ* ≥ 1000 para todos los números de Froude (Fig. 1). Esto significa
de manera concluyente, como en el caso de las ondas cinemáticas, que las
ondas dinámicas de Lagrange no están sujetas a difusión.
Está claro que las ondas dinámicas de Lagrange no son las típicas ondas de inundación.
Su tamaño es demasiado pequeño para constituir un verdadero riesgo.
Su aplicación se limita a la propagación de ondas cortas en canales de
irrigación y fuerza eléctrica, en los cuales la escala de la perturbación es tal que
típicamente
la onda puede percibirse a simple vista. A diferencia de las ondas de
inundación, que son ondas de masa que presentan una sola onda que
viaja aguas abajo, las ondas dinámicas clásicas son ondas de energía,
que presentan dos ondas que viajan en direcciones opuestas en flujo
subcrítico, y en una sola dirección, aguas abajo, en flujo supercrítico.
Ondas mixtas
En esta sección tratamos el otro tipo de onda que queda:
La onda cinemática-dinámica mixta, para abreviar, la onda "mixta" del flujo
no permanente en canales abiertos. Dado que, por definición, esta onda presenta
componentes tanto cinemáticos como dinámicos en cantidades comparables, se concluye que debe ser fuertemente difusiva.
La respuesta a esta pregunta es ¡Claro que sí! De hecho, la onda cinemático-dinámica mixta
es muy fuertemente difusiva. Es más: ¡Es la más difusiva de todas las ondas
consideradas en este trabajo! Ante este hecho, la pregunta que persiste es la de si la onda
mixta puede ser interpretada como una onda de inundación o no. Para responder con
precisión, recurrimos una vez más al esclarecedor trabajo de
Ponce y Simons (1977) y a su cálculo analítico de las funciones de celeridad y atenuación
para todo tipo de ondas en aguas poco profundas. Las cantidades de atenuación de las
ondas calculadas por Ponce y Simons se representan
en la Fig. 2 y se complementan con la Tabla 2.
Aclaramos que el decremento logarítmico δ define la cantidad de atenuación de la onda
(la reducción en la amplitud A) experimentada por una perturbación
sinusoidal en el tiempo transcurrido desde el tiempo t = 0 hasta t = 1, es decir,
transcurrido un período de propagación.
Dentro del rango σ*
mostrado en la Fig. 2, para flujos subcríticos (F < 1),
para los cuales la atenuación es más fuerte
(mayores valores de δ), se ve que el decremento logarítmico
varía desde un mínimo de δ = 0.0021 para σ* = 0.001 (Tabla 2, Línea 1), hasta un máximo (un valor pico)
de δ = 180 para σ* = 90 (Tabla 2, Línea 6).
La Tabla 2, Línea 0 muestra una cantidad muy pequeña de atenuación
de onda, 0,02% o 0,0002, asociada con un valor muy bajo de decremento logarítmico δ = 0,00021
correspondiente a
La Tabla 2, Línea 3a representa intencionalmente una atenuación de onda de 0,3 (Col. 4), es decir, una caída del 30% de la amplitud de la onda, un valor umbral considerado como la división entre las ondas difusivas (menor o igual al 30% de atenuación) y las ondas mixtas (más del 30% de atenuación) (Natural Environment Research Council, 1975).
La Tabla 2, Línea 4a representa intencionalmente una atenuación de onda de 0,99 (Col. 4), es decir, una caída del 99% de la amplitud de la onda, ¡un valor de atenuación que casi borra la onda por completo! Esta cantidad de atenuación corresponde a un valor de
La Tabla 2, Línea 5a (con fondo amarillo) representa intencionalmente una
atenuación de onda de 1,0 (Col. 4), es decir, una caída del 100 % de la amplitud
de la onda, ¡un valor de atenuación que borra la onda por completo! Esta
cantidad de atenuación corresponde a un valor de
En la Tabla 2, Col. 6 se muestran los tipos de onda indicados, desde la onda
cinemática, con atenuación muy pequeña (0,0002), hasta la onda difusiva, con atenuación pequeña a media (0,0021 a 0,1894), hasta la onda mixta, con atenuación grande a muy grande (0,3 a 0,9999).
En la Tabla 2, las Líneas 5 y 5a representan una onda inexistente; la onda ha desaparecido por completo y su masa ha pasado a formar parte del flujo subyacente.
Dado que la atenuación de la onda es A = (1 - eδ) (Tabla 2, Col. 5), los resultados de la Tabla 2 conducen a los siguientes tipos de ondas y sus rangos correspondientes:
Concluimos que la mayoría, si no todas, las ondas mixtas habrían perdido efectivamente toda su fuerza en la mayoría de los casos de interés práctico. Estas ondas pierden su fuerza rápidamente debido a su naturaleza altamente difusiva, esta última debido a la competencia entre términos cinemáticos y dinámicos (léase fuerzas) comparables en tamaño. De ello se deduce que las ondas mixtas carecen de una propiedad básica de una onda de inundación, a saber, su permanencia, que se caracteriza por una atenuación (difusión) leve o muy leve. Por lo tanto, es aparente que, en general, las ondas mixtas no pueden interpretarse como ondas de inundación.
Onda de inundación por rotura de presa
Toda regla tiene una excepción. En la sección anterior,
presentamos una justificación matemática elaborada de por qué la
onda mixta no es probable que se aplique al caso de una
inundación general, es decir, una que está sujeta a muy poca
o ninguna atenuación. Sin embargo, existe una ola
de inundación en particular que puede difusionarse
apreciablemente. Éste es el caso de una onda de inundación causada por la rotura de una presa.
Normalmente, la onda de inundación producida por la ruptura de una presa
de tierra dura aproximadamente 3 horas, lo cual la hace
un candidato seguro para una fuerte difusión de la onda.
Estas ondas de inundación (Fig. 3) tienden a caer en la categoría de ondas mixtas o, como mínimo, ser una onda de difusión fuertemente difusiva, con una atenuación
A ≅ 0.3
(consulte la Tabla 2, Línea 3a). Afortunadamente, los casos de rotura de presas son raros.
Análisis y conclusiones
Hemos analizado las propiedades de celeridad y atenuación de varios tipos de ondas
de aguas poco profundas actualmente utilizadas en ingeniería hidráulica: (1) cinemáticas,
(2) difusivas, (3) mixtas, y (4) dinámicas. Las ondas cinemáticas
son masivas (léase "grandes") y de hecho no difusivas.
Hemos tratado de responder a la pregunta de si la onda mixta es generalmente demasiado difusiva
para ser considerada una onda de inundación práctica. La respuesta es ¡Sí! En la gran
mayoría de los casos, es posible que las ondas mixtas no estén ahí para que las
calculemos. Su típico tamaño mediano les obliga a atenuarse muy rápidamente, y su
masa se une eventualmente a la onda cinemática o difusiva subyacente,
la cual continúa creciendo tanto en tamaño como en permanencia a medida que se propaga aguas abajo.
Téngase en cuenta que sólo en el caso extremadamente inusual de una onda de inundación
que resulte de la rotura de una presa podríamos enfrentarnos al caso de una onda mixta.
Una onda de inundación que rompe una presa es característicamente repentina, preparada
por la Naturaleza para constituir una onda mixta, un tipo inusual de onda de
inundación [La experiencia de la falla de la presa de Teton (Fig. 3) es un
ejemplo de ello]. Los profesionales encargados de pronosticar o pronosticar retrospectivamente
una ola de inundación tras la rotura de una presa estarían interesados en
tener esto en cuenta. Para todas las demás aplicaciones de enrutamiento de
ondas de inundaciones, las ondas cinemáticas y difusivas deben hacer el trabajo de manera directa y precisa.
En particular, dado que una onda difusiva en realidad calculará la difusión, incluido el caso de
difusión cero, se deduce que la solución de una onda difusiva abarca la solución de una onda cinemática.
Por lo tanto, la onda difusiva se postula como la onda de inundación recomendada, es decir,
el tipo de onda generalmente indicada para su uso en aplicaciones prácticas de enrutamiento, y otras aplicaciones en
análisis y diseño.
En general, las ondas cinemáticas-dinámicas mixtas, aquí denominadas simplemente "ondas mixtas",
y que en otros lugares se han denominado ampliamente, postulamos aquÍ, de manera inexacta, "ondas dinámicas",
de hecho no son lo suficientemente grandes ni lo suficientemente permanentes como para constituir
verdaderas ondas de inundación. Un exhaustivo conjunto de teoría y experiencia confirma
este hecho. Por otro lado, las ondas cinemáticas y sus primas cercanas, las ondas difusivas,
suelen presentar una gran masa y son característicamente no difusivas, es decir, no se atenúan,
o se atenúan sólo una cantidad muy pequeña; por lo tanto, tienden a ser modelos
ideales de ondas de inundación. Dado que la solución numérica de una onda difusiva
generalmente comprende la de una onda cinemática, la onda difusiva puede considerarse
como la forma más apropiada de modelar ondas de inundación.
Referencias
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York, NY.
Cunge, J. A. 1969. On the
Subject of a Flood Propagation Computation Method (Muskingum Method).
Journal of Hydraulic Research, 7(2), 205-230.
Fread, D. L. 1985. "Channel Routing," en Hydrological Forecasting,
M. G. Anderson y T. P. Burt, eds., Wiley, New York.
Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute,
No. 1, Diciembre.
Lagrange, J. L. de. 1788. Mécanique analytique, Paris, part 2, section II, articulo 2, 192.
Lighthill, M. J. y G. B. Whitham. 1955.
On kinematic waves. I. Flood movement in long rivers.
Proceedings,
McCarthy, G.T. 1938. "The Unit Hydrograph and Flood Routing,"
unpublished manuscript, presented at a Conference of the North Atlantic Division,
U.S. Army Corps of Engineers, June 24.
(Citado por el texto de V. T, Chow "Open-channel Hydraulics," página 607).
Natural Environment Research Council. 1975. Flood Studies Report,
Vol. III: Flood Routing Studies, Londres, Inglaterra.
Ponce, V. M. y D. B. Simons. 1977.
Shallow wave propagation in open channel flow.
Journal of Hydraulic Engineering, ASCE, 103(12), 1461-1476.
Ponce, V. M. y D. Windingland. 1985.
Kinematic shock:
Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, 111(4), April, 600-611.
Ponce, V. M. 1995.
Hydrologic and environmental impact of the Parana-Paraguay
waterway on the Pantanal of Mato Grosso, Brazil.
https://ponce.sdsu.edu/hydrologic_and_environmental_impact_of_the_parana_paraguay_waterway.html
Ponce, V. M. 2014.
Engineering Hydrology: Principles and Practices.
Texto en línea.
Seddon, J. A. 1900. River Hydraulics. Transactions, American Society of Civil Engineers, Vol. XLIII, 179-243, Junio; Extracto: páginas 218-223.
Taher-Shamsi, A., A. V. Shetty, y V. M. Ponce. 2003.
Embankment dam breaching: Geometry and peak outflow characteristics.
Documento en línea. En Español: https://ponce.sdsu.edu/geometria_y_caracteristicas_del_caudal_pico_de_salida.html
Wylie, C. R. 1966. Advanced Engineering Mathematics, 3rd ed., McGraw-Hill Book Co., Nueva York.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||