1. INTRODUCCIÓN El cálculo de las propiedades geométricas de una sección parabólica de canal se hace aplicando integrales normales y de línea, usando los parámetros que caracterizan una parábola.
2. PROPIEDADES GEOMÉTRICAS DE UNA SECCIÓN PARABÓLICA
La ecuación de Manning es:
en la cual Q = caudal; A = área; R = radio hidráulico; So = pendiente de fondo; y n = rugosidad de Manning. Por lo tanto:
en la cual el factor de sección Fs está dado de la siguiente forma:
Por lo tanto:
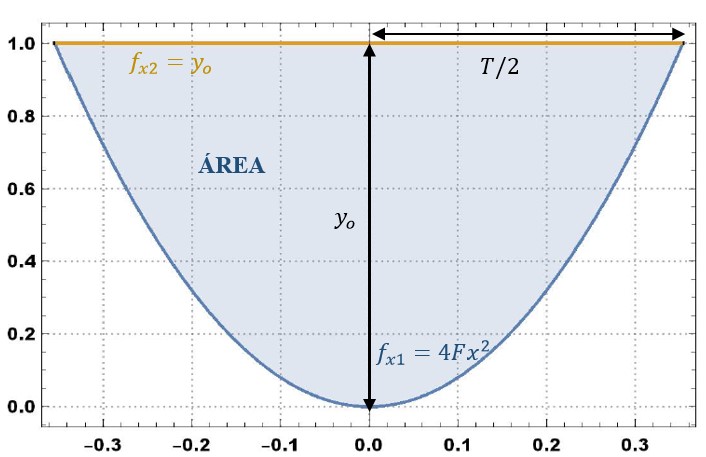
El área y el perímetro de una sección parabólica para un tirante yo y ancho de superficie libre T se muestran en la Fig. 1.
Fig. 1 Esquema de definición de una sección parabólica. Para calcular el área se hace uso de la siguiente integral:
en la cual 4F es un parámetro de la parábola definido como sigue:
Por lo tanto:
Reemplazando la Ec. 10 en la Ec. 8:
Por lo tanto:
Para el perímetro mojado, se utiliza una integral de línea:
La Ecuación 14 tiene la forma de una integral conocida: ∫ (a2+x2)1/2dx, y su solución es:
Reemplazando la Ec. 10 en la Ec. 16, se obtiene:
La Ecuación 19 se puede expresar en función de logaritmos, usando la siguiente fórmula:
Por lo tanto:
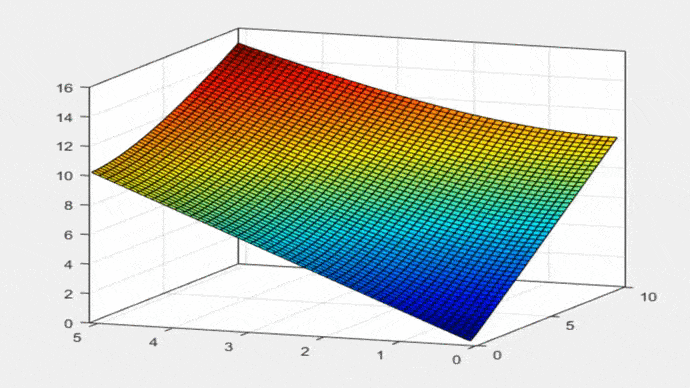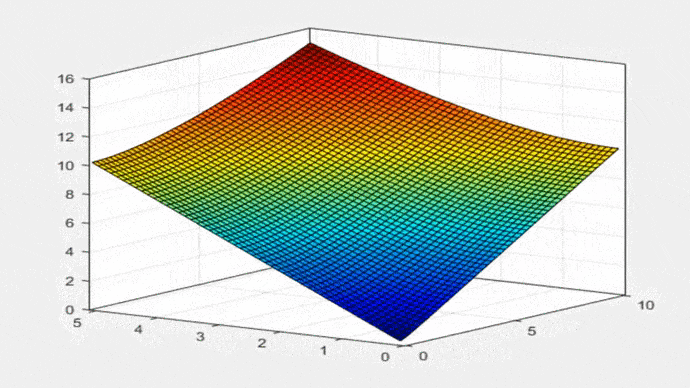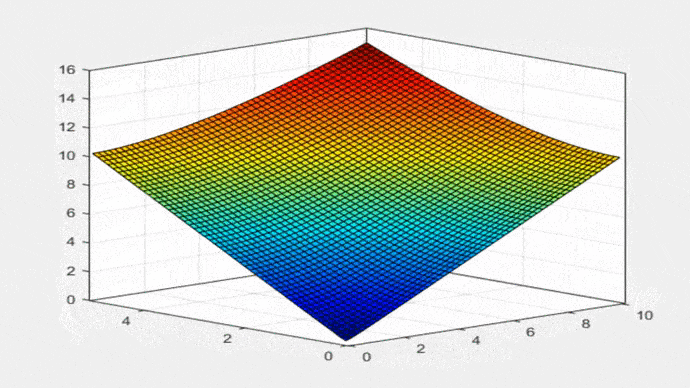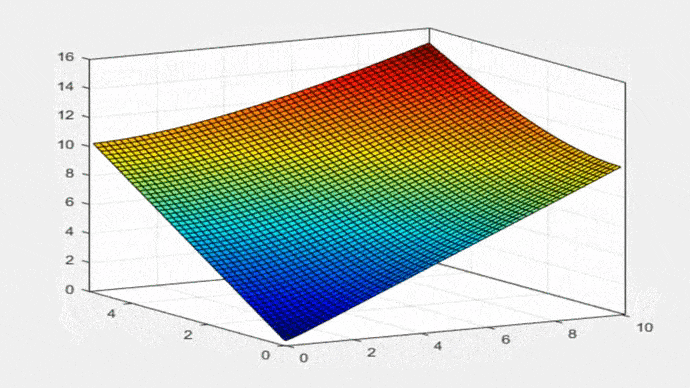
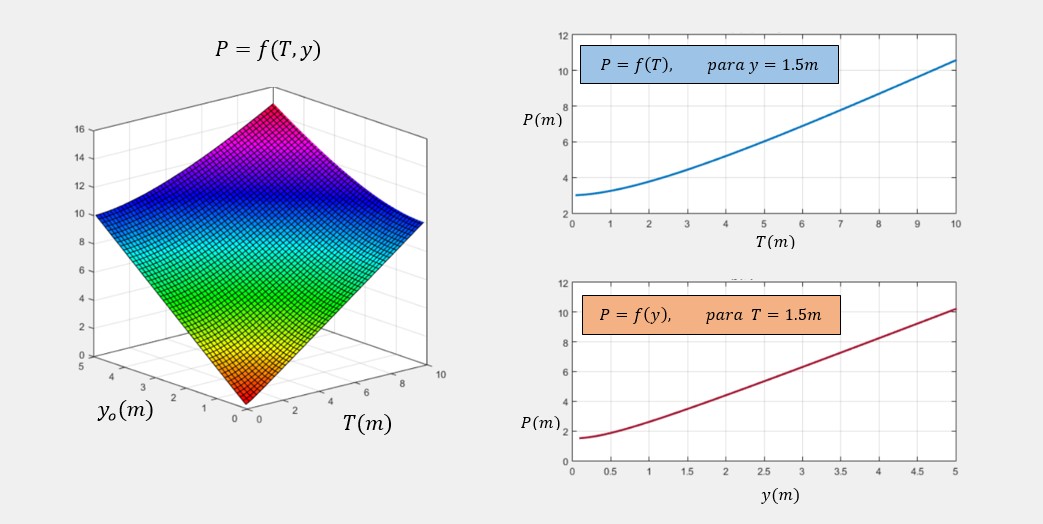
La Ecuación 21 es la misma fórmula que aparece en la Tabla 2-1 del libro de Ven Te Chow (1994): “Hidráulica de Canales Abiertos”. La Figura 2 muestra la Ecuación 19 en forma gráfica: P = f (T,yo), para 0 < T < 10; 0 < yo < 5:
Fig. 2 Perímetro mojado versus el ancho de la superficie libre y tirante de agua. A continuación, se utiliza la Ec. 19 para construir las propiedades geométricas de la parábola. El ancho de superficie libre T es:
El radio hidráulico R es:
El tirante hidráulico D es:
Por lo tanto:
La Tabla 1 resume las propiedades de una sección parabólica.
APÉNDICE I. BIBLIOGRAFÍA
Chow, V. T. 1994. Hidráulica de Canales Abiertos. McGraw-Hill Interamericana, S.A., Bogotá,
Colombia.
Leithold, L. 1998. El Cálculo, Séptima Edición, Oxford University
Press, Harla México, S.A.
APÉNDICE II. NOTACIÓN
En este documento se utilizan los siguientes símbolos:
Q = caudal;
n = coeficiente de Manning;
So = pendiente de fondo;
yo = tirante de agua;
Fs = factor de sección;
A = área de flujo;
P = perímetro mojado;
T = ancho de la superficie libre;
R = radio hidráulico; y
D = tirante hidráulico.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 210224 |
| Los documentos en Portable Document Format (PDF) requieren Adobe Acrobat Reader 5.0 o mas alto para visualizar; descargar Adobe Acrobat Reader. |