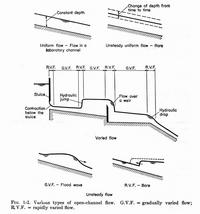
|
|
CIVE 530 - OPEN-CHANNEL HYDRAULICS
LECTURE 1: INTRODUCTION
|
|
1.1 OPEN-CHANNEL FLOW VS. PIPE FLOW
|
- Open-channel flow has free surface subject to atmospheric pressure.
- Pipe flow (closed-conduit) flow has only hydraulic pressure.
- Open-channel flow problems are more complicated than closed-conduit flow problems.
- The free surface is likely to vary in space (varied) and time (unsteady).
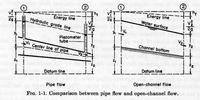
Fig. 1-1 (Chow)
|
|
- In pipes, the cross section is fixed; in channels it varies.
- In pipes, the roughness may vary from smooth brass to corroded pipes.
- In channels, roughness varies from plastic flumes (n = 0.008) to flood plains
(n ≈ 0.1-0.2).
- Furthermore, roughness may vary with the flow level.
- Recent experience suggests that values of equivalent Manning roughness applicable to the wetlands of South Florida
may be as high as n = 1.
- In channels that move their bed, there may be ripples and dunes, or plane bed. (Page 553 of Engineering Hydrology)
- Storm sewer flow looks like pipe flow, but it behaves like channel flow.
|
1.4 LAMINAR VS TURBULENT FLOW
|
- The Darcy-Weisbach friction factor equation, applicable to pipe flow, is:
- in which hf = head loss, f = Darcy-Weisbach friction factor, do = pipe diameter; L = pipe length.
- Since:
|
R = A/P = [(1/4) πdo2] /(π do) = do/4
|
- Then:
- The energy gradient, or energy slope, is:
|
S = hf / L = f U2/(8gR) = (f/8) (D/R) F2
|
- where D= hydraulic depth:
- where T = top width, and F is the Froude number:
- In a hydraulically wide channel: D ≈ R. Therefore:
- where f' = f/8.
- In laminar flow, the Darcy-Weisbach friction factor f is inversely proportional to the Reynolds number
(f is in the range 0.04-0.40):
- K depends only on channel shape: K = 24 for rectangular channels; K = 14 for triangular channels.
- In turbulent flow, K is less dependent on Re.
- The Prandtl-von Karman equation:
|
1/(f)1/2 = 2 log [Re(f)1/2] + 0.4
|
- In turbulent flow, f is in the range 0.016-0.040.
- f' is on the order 0.002-0.005.
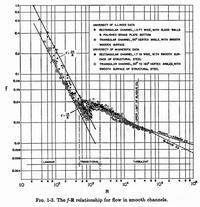
Fig. 1-3 (Chow)
|
|
- The friction equation, applicable to
hydraulically wide channels, is:
- For slope S constant, an increase/decrease in f' causes a decrease/increase in F.
- For friction f' constant, an increase/decrease in S causes an increase/decrease in F.
- For Froude F constant, an increase/decrease in f' causes an increase/decrease in S.
Go to Chapter 2.
|