CIVE 530 - OPEN-CHANNEL HYDRAULICS
LECTURE 8C: DIRECT STEP METHOD FOR WATER-SURFACE PROFILE COMPUTATION

EXAMPLE

Calculate an M₂ and S₂ profile, upstream and downstream of a change in grade, from mild to steep.

The discharge is 2000 m³/s.
The channel bottom width is 100 m.
The side slope is 2: 1 (H:V).
The upstream slope is 0.0001.
The upstream channel Manning's n is 0.025.
The downstream slope is 0.03.
The downstream channel Manning's n is 0.045.

SOLUTION.-
Use ONLINE CHANNEL 05 to determine normal depth and velocity, and critical depth and velocity, in upstream and downstream channels.
The results of ONLINE CHANNEL 05 for the upstream channel are:
1. Critical depth = 3.364 m
2. Critical velocity = 5.571 m/s
3. Normal depth = 10.098 m
4. Normal velocity = 1.648 m/s
5. Normal Froude number = 0.179

The results of ONLINE CHANNEL 05 for the downstream channel are:
1. Critical depth = 3.364 m
2. Critical velocity = 5.571 m/s
3. Normal depth = 2.669 m
4. Normal velocity = 7.113 m/s
5. Normal Froude number = 1.425

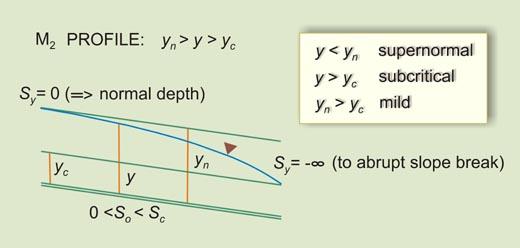
Calculation of the critical slopes:
Upstream channel:
S_c = n²V_c² / R_c^4/3
y_c= 3.364
A_c = (b + zy_c) y_c = 359.033
P_c = b + 2(1 + z²)^1/2y_c = 115.044
R_c = A_c / P_c = 3.1208
S_c = n²V_c² / R_c^4/3 = (0.025)² (5.57)² / (3.1208)^4/3 = 0.00425
Use ONLINE CHANNEL 04: S_c = 0.00425.
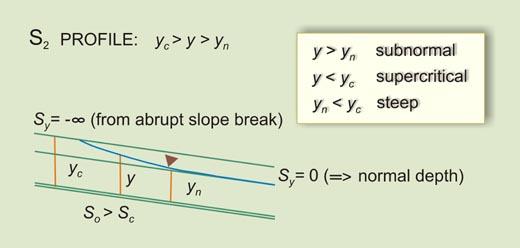
Downstream channel:
S_c = n²V_c² / R_c^4/3
y_c= 3.364
A_c = (b + zy_c) y_c = 359.033
P_c = b + 2(1 + z²)^1/2y_c = 115.044
R_c = A_c / P_c = 3.1208
S_c = n²V_c² / R_c^4/3 = (0.045)² (5.57)² / (3.1208)^4/3 = 0.0138

Use ONLINE CHANNEL 04: S_c = 0.0138.

Formulas:
Flow area:     A = (b + zy) y          (1)

Wetted perimeter:     P = b + 2(1 + z²)^1/2y          (2)

Hydraulic radius:     R = A / P          (3)

Friction slope:     S_f = n²V² / R^4/3          (4)
Average (reach) friction slope:     S_f _ave = 0.5 ( S_{f ₁} + S_{f ₂} )          (5)
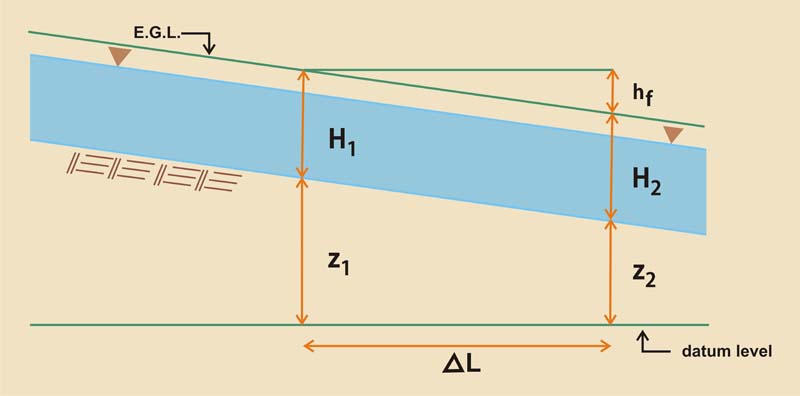
Increment along the channel ΔL:

Upstream section 1

Downstream section 2

h_f = head loss

Bernoulli equation (total head):

H₁ + z₁ = H₂ + z₂ + h_f

Fig. 1 Definition sketch for calculation of channel length increment ΔL.

S_f_ave = h_f / ΔL

H₁ + z₁ = H₂ + z₂ + S_f_ave ΔL

z₁ - z₂ = H₂ - H₁ + S_f_ave ΔL

z₁ - z₂ - S_f_ave ΔL = H₂ - H₁

S_o = (z₁ - z₂) / ΔL

S_o ΔL - S_f_ave ΔL = H₂ - H₁

(S_o - S_f_ave) ΔL = H₂ - H₁

ΔL = (H₂ - H₁) / (S_o - S_f_ave)

ΔL = (ΔH)/ (S_o - S_f _ave)          (6)

The sign is the sign of the denominator: negative u/s in M₂ profile, and positive d/s in S₂ profile.

Table 1. Calculation of backwater curve, U/S channel, M₂ curve, S_o = 0.0001.

[x] = columns; (y) = equations

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12]

y A V V²/(2g) H P R S_f S_f _ave ΔH ΔL ∑L

y (1) Q/[2] [3]²/(2g) [1] + [4] (2) (3) (4) average slope
(5) H₂ - H₁ change in L
(6) cum ΔL

3.364 359.033 5.570 1.581 4.945 115.044 3.1208 0.00425 --- --- --- 0

4.000 432.000 4.630 1.092 5.092 117.888 3.664 0.00237 0.00331 0.147 -45.794 -45.794

5.000 550.000 3.636 0.674 5.674 122.360 4.495 0.00111 0.00174 0.528 -354.878 -400.672

6.000 672.000 2.976 0.451 6.451 126.833 5.298 0.00060 0.000855 0.777 -1029.139 -1429.811

7.000 ? ? ? ? ? ? ? ? ? ? ?

8.000 ? ? ? ? ? ? ? ? ? ? ?

9.000 ? ? ? ? ? ? ? ? ? ? ?

10.000 ? ? ? ? ? ? ? ? ? ? ?

10.097 ? ? ? ? ? ? 0.0001 ? ? ? ∞

ANSWER: The flow depth is 6 m at a distance of 1429.811 m upstream from the brink.

Table 2. Calculation of backwater curve, D/S channel, S₂ curve, S_o = 0.03.
[x] = columns; (y) = equations
[1]	[2]	[3]	[4]	[5]	[6]	[7]	[8]	[9]	[10]	[11]	[12]
y	A	V	V²/(2g)	H	P	R	S_f	S_f _ave	ΔH	ΔL	∑L
y	(1)	Q/[2]	[3]²/(2g)	[1] + [4]	(2)	(3)	(4)	average slope (5)	H₂ - H₁	change in L (6)	cum ΔL
3.364	359.033	5.570	1.581	4.945	115.044	3.1208	0.0138	---	---	---	0
3.3	351.780	5.685	1.647	4.9475	114.758	3.0654	0.0147	0.01425	0.002	0.127	0.127
3.2	340.48	5.874	1.759	4.9586	114.311	2.979	0.0163	0.0155	0.0111	0.765	0.892
3.1	329.22	6.075	1.881	4.981	113.864	2.891	0.0181	0.0172	0.0224	1.750	2.642
3.0	?	?	?	?	?	?	?	?	?	?	?
2.9	?	?	?	?	?	?	?	?	?	?	?
2.8	?	?	?	?	?	?	?	?	?	?	?
2.7	?	?	?	?	?	?	?	?	?	?	?
2.669	?	?	?	?	?	?	0.03	?	?	?	∞

ANSWER: The flow depth is 3.1 m at a distance of 2.642 m downstream from the brink.

COMMENTS:

Start at critical depth, go to normal depth.
Use a reasonably small interval; accuracy depends on it (due to the averaging of friction slope).
L is positive in the downstream direction, negative upstream.
Direct step method is for prismatic (artificial) channels: direct calculation of distance from step; no iteration.

081023