OPEN CHANNELS I
CHAPTER 4 (1) - ROBERSON ET AL., WITH ADDITIONS

|
Cabana irrigation canal, Peru.
- IN A NATURAL CHANNEL, THE PROBLEM IS OF PREDICTING THE WATER SURFACE PROFILE, OR TO ESTIMATE VELOCITY AND DEPTH.
- STEADY UNIFORM FLOW: WHEN DISCHARGE, VELOCITY AND DEPTH ARE CONSTANT.
- STEADY GRADUALLY VARIED FLOW: WHEN VELOCITY AND DEPTH ARE A FUNCTION OF DISTANCE.
- UNSTEADY FLOW: WHEN DISCHARGE, VELOCITY, AND DEPTH ARE A FUNCTION OF TIME AND DISTANCE.
- ALL ASPECTS OF THE DESIGN PROBLEM MUST BE CONSIDERED, INCLUDING WATER AND SEDIMENT TRANSPORT.
- UNUSUAL HAZARDS:
-- LANDSLIDES
-- SEDIMENTATION
-- ACCIDENTAL GATE OPERATION
-- BREACH OF EMBANKMENT
- IN STEEP CHANNELS, THERE IS THE POSSIBILITY OF ROLL WAVES.

|
Roll waves in Cabana lateral canal, Peru.
- ROLL WAVES CAN BE AVOIDED WITH SEQUENTIAL DROPS.

|
Drops in steep La Joya canal, Peru.
- STEADY UNIFORM FLOW:
- ARTIFICIAL CHANNELS: THERE IS NO CHANGE IN VELOCITY AND FLOW DEPTH.
- VELOCITY HEAD IS CONSTANT.
- EGL AND W.S. WILL HAVE SAME SLOPE AS CHANNEL BOTTOM.
- PRISMATIC CHANNEL: CHANNEL OF CONSTANT CROSS SECTION.
- NORMAL DEPTH: FLOW IN UNIFORM CHANNEL.
- NET FORCE ACTING ON FLOW IS ZERO.
- ALL FORCES ARE BALANCED.
- GRAVITATIONAL FORCE EQUALS RESISTANCE
FORCE.

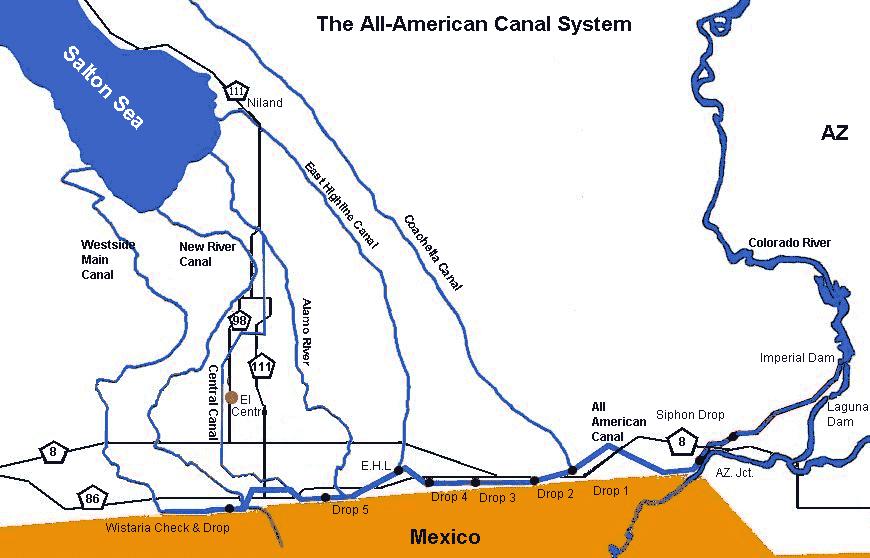
- THE FORCE BALANCE EQUATION IS:
- W sin θ = τo P Δx
- τo = SHEAR STRESS ALONG THE BOTTOM
- θ = ANGLE OF INCLINATION OF CHANNEL BOTTOM
- P = WETTED PERIMETER OF CHANNEL CROSS SECTION
|
Gravitational and resistance forces under uniform flow.
- SINCE: W = γ A Δx
- γ A Δx sin θ = τo P Δx
- τo = γ (A/P) sin θ
- BECAUSE θ IS SMALL: sin θ ≅ tan θ = So
- τo = γ (A/P) So
- τo = γ R So
- R = HYDRAULIC RADIUS
- THE SHEAR STRESS CAN ALSO BE EXPRESSED AS THE QUADRATIC LAW:
- τo = Cd ρ V2 = Cd (γ/g) V2
- Cd IS A DRAG OR FRICTION COEFFICIENT, WHICH IS DIMENSIONLESS
N/M2 = Cd [(N/M3)/(M/S2) ] (M2/S2)
- Cd ρ V2 = γ R So
- V = (g/Cd) 0.5 (R So) 0.5
- V = C (R So) 0.5
- C = CHEZY COEFFICIENT
- Cd = f/8
- IF f = 0.024, Cd = 0.003
- V = (8g/f) 0.5 (R So) 0.5
- THIS IS A FORM OF THE DARCY-WEISBACH EQUATION APPLIED TO OPEN CHANNELS
- V2= (8g/f) R So
- V2= (8g/f) R (hf/L)
- V2= (2g/f) 4R (hf/L)
- hf = f [L/(4R)] (V2/ 2g)
- THIS IS THE SAME AS DARCY-WEISBACH, BUT WITH (4R) INSTEAD OF D.
- SINCE 4R = D IN A PIPE, THE HYDRAULIC RADIUS IS AN EQUIVALENT MEASURE OF CROSS SECTION IN AN OPEN CHANNEL
- R = A/P = [πD2/4]/(πD) = D/4
- V = (8g/f)0.5 (R So)0.5
- Q = A V = (8g/f) 0.5 A (R So)0.5
- IN ROCK-BEDDED STREAMS:
- f = [1.2 + 2.3 log (R/d84) ]-2
- d84 = diameter for which 84% by weight is smaller.

|
Rock Creek near Darby, Montana.
- HYDRAULIC DEPTH IN A CHANNEL: D = A/T
- HYDRAULIC RADIUS: R = A/P
- IN A WIDE CHANNEL: T ≅ P
- THEREFORE: R ≅ D
- V = (8g/f)0.5 (D So)0.5
- V2 = (8g/f) D So
- So = (f/8) [V2/(gD)]
- So = (f/8) F2
- F IS THE FROUDE NUMBER = V /(gD)0.5
- For F = 1: So = Sc = f/8
- So = Sc F2
- EXAMPLE 4-1
- DETERMINE THE DISCHARGE IN A LONG, RECTANGULAR CONCRETE CHANNEL THAT IS 5-FT WIDE, SLOPE = 0.002, AND WITH SECTION DEPTH = 2 FT.
- ASSUME ROUGHNESS OF CONCRETE ks = 0.005 ft. (range for concrete 0.001-0.01)
- A = (2) (5) = 10
- R = A/P = 10 /( 2 + 2 + 5) = 1.11 FT.
- ks / (4R) = (0.005) /(4 X 1.11) = 0.00113
- ASSUME REYNOLDS NUMBER Re = 106
- FROM MOODY DIAGRAM: f ≅ 0.02
- FIRST TRIAL OF Q:
- Q = (8g/f) 0.5 A (R So)0.5
- Q = [(8)(32.2)/(0.02) ]0.5 10 [(1.11)(0.002)]0.5
- Q = 53.5 CFS
- V = Q/A = 5.35 FPS
- ASSUME TEMPERATURE = 60 oF
- KINEMATIC VISCOSITY ν = 1.22 X 10-5 FT2/SEC
- Re = V (4R)/ν = 5.35 (4) (1.11) / 0.0000122 = 1.95 X 106
- FROM MOODY DIAGRAM: f ≅ 0.02
- THEN: Q = 53.5 CFS.
- WHEN THE CHEZY COEFFICIENT IS NOT A CONSTANT, BUT RATHER A FUNCTION OF THE HYDRAULIC RADIUS:
- C = (1.49/n) R1/6
- CHEZY EQUATION: V = C (R So)1/2
- MANNING EQUATION: V = (1.49/n) R1/6 (R So)1/2
- MANNING EQUATION: V = (1.49/n) R 2/3 So1/2
- DISCHARGE: Q = (1.49/n) A R 2/3 So1/2
- CALCULATION OF EXAMPLE b = 5 ft; y = 2 ft; z = 0; S = 0.002. ASSUME n = 0.013
- RESULT: Q = 54.83 CFS (COMPARE WITH PREVIOUS RESULT).
- THE RESISTANCE FACTOR IN OPEN CHANNELS IS A FUNCTION OF THE CHANNEL ROUGHNESS, AMONG OTHER FACTORS.
- THE RESISTANCE FACTOR IN FLOOD PLAINS.
THE MANNING EQUATION
- HIGHWAY CULVERTS AND URBAN SEWERS ARE EXAMPLES OF CIRCULAR OPEN CHANNELS.
- THE DISCHARGE IS PROPORTIONAL TO A R2/3
- THE VELOCITY IS PROPORTIONAL TO R2/3
FLOW IN CIRCULAR CONDUITS

|
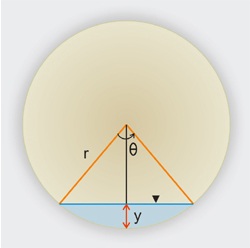
- THE RATIO Q/Qo = (A R2/3)/(Ao Ro2/3) IS INDEPENDENT OF THE ROUGHNESS OR SLOPE, WHERE Q IS DISCHARGE FOR A GIVEN DEPTH AND Qo IS THE DISCHARGE WHEN THE CONDUIT FLOW FULL (CONSTANT n ASSUMED).
- THE MAXIMUM DISCHARGE OCCURS AT A DEPTH LESS THAN FULL.
- AS THE CONDUIT GETS FULL, THE WETTED PERIMETER INCREASES MUCH FASTER THAN THE AREA, THUS DECREASING THE HYDRAULIC RADIUS.
|
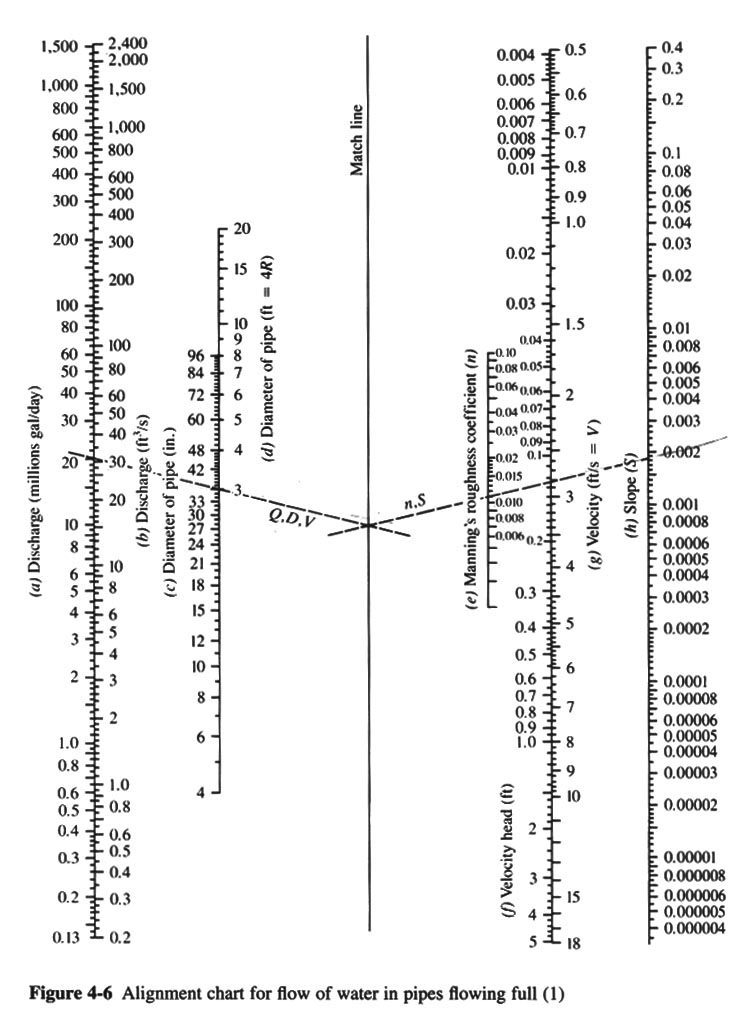
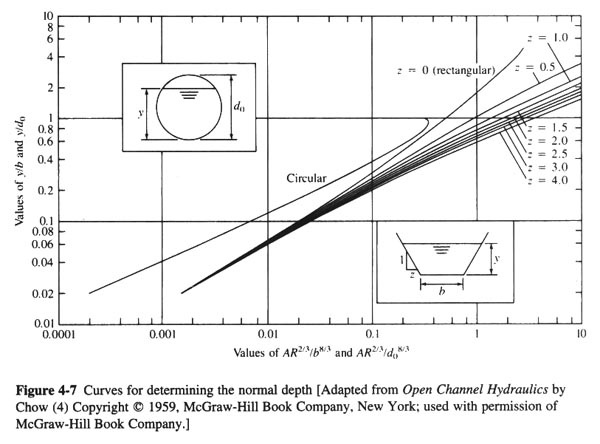
- USE FIG. 4-6, WITH n = 0.012 and S= 0.0019. FROM THIS FIGURE: Qo = 30 CFS.
EXAMPLE 4-2
DETERMINE THE DISCHARGE IN A 3-FT DIAMETER SEWER PIPE IF THE DEPTH OF FLOW IS 1 FT, SLOPE = 0.0019, n = 0.012.
|
- y/do = 0.3333
- FROM FIG. 4-5: Q/Qo = 0.2
- Q = 0.2 Qo = 0.2 (30) = 6 CFS.
- COMPARE WITH ONLINE CALCULATION.
- RESULT: Q = 7.55 CFS (THERE IS A SLIGHT DIFFERENCE).
- TO ASSIST IN SOLVING PROBLEMS INVOLVING THE FLOW IN TRAPEZOIDAL CHANNELS:
- THE DIMENSIONLESS FACTOR AR2/3/b8/3 IS
PLOTTED VS y/b (Fig. 4-7).
EXAMPLE 4-3
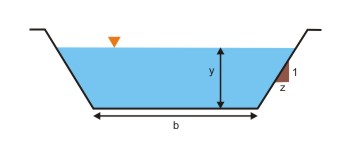
DETERMINE THE NORMAL DEPTH FOR A TRAPEZOIDAL CHANNEL WITH THE FOLLOWING CHARACTERISTICS:
- SIDE SLOPES OF 1 VERTICAL TO 2 HORIZONTAL (z = 2);
- b = 8 ft, Q = 200 cfs, So= 0.001, n = 0.012.
FLOW IN CONDUITS OF TRAPEZOIDAL CROSS
SECTION
|
- THE MANNING EQUATION (EQ. 4-7) CAN BE WRITTEN AS:
- A R2/3 = Q n / (1.49 So1/2 )
- A R 2/3/b8/3 = Q n / (1.49 So1/2b8/3)
- SINCE: Q = 200 CFS, n= 0.012; So= 0.001; b= 8 ft
- EVALUATE THE RIGHT-HAND SIDE:
- A R2/3/b8/3 = 200 (0.012) / [1.49 (0.001)1/2(8)8/3]
- A R 2/3/b8/3 = 0.199
- FROM FIG. 4-7: y/b = 0.33.
|
- THEN: y = 0.33 (8) = 2.64 FT.
- COMPARE WITH ONLINE CALCULATION.
- RESULT: y = 2.63 FT (SAME RESULT).
- THE CHANNEL WILL ERODE IF THE VELOCITY IS TOO LARGE.
- TWO METHODS:
-- PERMISSIBLE VELOCITY METHOD
-- PERMISSIBLE TRACTIVE FORCE METHOD.
- DESIGN PROCEDURE:
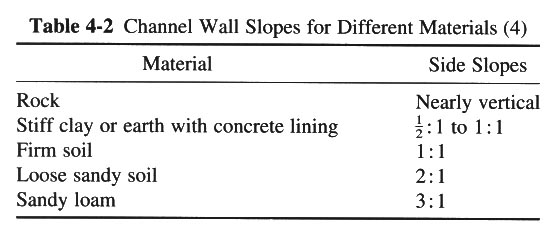
-- CHOOSE SIDE SLOPE z THAT WOULD BE STABLE (TABLE 4.2).
DESIGN OF ERODIBLE CHANNELS
|
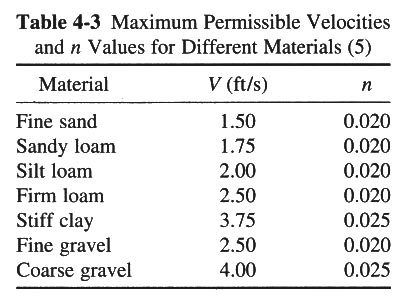
-- CHOOSE MAXIMUM PERMISSIBLE VELOCITY V (TABLE 4.3).
|
-- WITH Q, V, n, S, and z, CALCULATE b AND y.

|
All-American Canal, near Yuma, California.
- CHOOSE SIDE SLOPE z = 1.5 H : 1 V (TABLE 4-2)
- CHOOSE V= 2.5 FPS (TABLE 4-3)
- CHOOSE n= 0.020.
- CALCULATE HYDRAULIC RADIUS FROM MANNING EQUATION:
- V = (1.49/n) R2/3S 1/2
- R = [nV/(1.49S1/2)]3/2 =
- R = [(0.02)(2.50) /(1.49 X 0.00061/2)] 3/2 = 1.6
- A = Q/V = 100/2.5 = 40 sq ft.
- P = A/R = 40/1.6 = 25.
- A = y ( b + 1.5 y) = by + 1.5 y2 = 40
- P = b + 2 (y2 + 1.52y2 ) 1/2 = b + 3.61y = 25
- b = 18.1; y = 1.91; say b = 18.0 and y = 2.0
- COMPARE WITH ONLINE CALCULATION, ASSUMING B = 18 FT.
- RESULT: V = 2.5 FPS; y = 1.92 FT (SAME RESULT).
EXAMPLE 4-4
AN UNLINED IRRIGATION CANAL IS TO BE CONSTRUCTED IN A FIRM LOAM SOIL. THE SLOPE IS 0.0006, AND Q = 100 CFS. DETERMINE THE CHANNEL DIMENSIONS z, b AND y.
- WATER RESOURCES PROJECTS INCLUDES OTHER STRUCTURES IN ADDITION TO CHANNELS
- INTAKE WORKS, FLUMES, CHECKS, DROPS, AND TRANSITIONS.
PROJECT SCOPE

|
Crossing of Tinajones Feeder Canal with Chiriquipe Creek, Peru.

|
Creek crossing with Wellton-Mohawk Feeder Canal, Arizona.

|
Drops in Cabana lateral canal, Peru.
- DIVERSION DAM IS CONSTRUCTED SO AS TO MAINTAIN A WATER LEVEL HIGH ENOUGH IN THE RIVER TO BE ABLE TO ALWAYS DIVERT THE REQUIRED FLOW INTO THE MAIN IRRIGATION CANAL.
- THE INTAKE TO THE MAIN CANAL CONSISTS OF A CANAL ENTRANCE STRUCTURE, INCLUDING GATES FOR CONTROLLING THE DISCHARGE INTO THE CANAL.
- WASTEWAYS ARE OFTEN PROVIDED AT INTERVALS ALONG THE MAIN CANAL IF AN EMERGENCY DEVELOPS WHERE DOWNSTREAM WATER USE IS STOPPED.
- A FLUME IS USED TO CONVEY WATER ACROSS A DEPRESSION.

|
Dulzura flume (conduit), downstream of Barrett Dam, San Diego County
(Note that the flume was overflowing on March 8, 2005).
- AN INVERTED SIPHON COULD BE USED FOR THIS PURPOSE.

|
Inverted siphon, Cabana irrigation canal, Peru.
- TRANSITIONS ARE REQUIRED FOR SMOOTH PASSAGE OF WATER FROM CANAL TO FLUME.
- CHECK STRUCTURE CONTROLS WATER SURFACE LEVEL ON A CANAL TO MAINTAIN HIGH WATER SO THAT WATER CAN BE DIVERTED INTO SECONDARY CANAL.
- DROP STRUCTURE IS A VERY STEEP CHANNEL.

|
Tinajones Feeder canal drop, Peru.
- BAFFLED DROP STRUCTURE IS SHOWN IN FIG. 4-10.
- SECONDARY CANAL DRAWS WATER FROM THE CANAL THROUGH THEIR OWN INTAKE STRUCTURES.
- FARM LATERALS TAKE WATER FROM THE
SECONDARY CANALS.
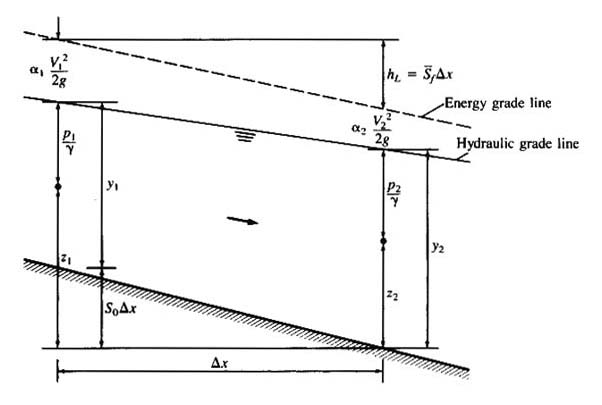
- THE ENERGY EQUATION IS:
- p1/γ + α1V12/(2g) + z1 = p2/γ + α2V22/(2g) + z2 + hL
- p1/γ = pressure head at point 1
- α1V12/(2g) = velocity head at point 1
- z1 = elevation (head) at point 1
- hL = head loss between points 1 and 2
STEADY-NONUNIFORM FLOW IN OPEN
CHANNELS
|
- p1/γ + z1 = y1 + So Δx
- p2/γ + z2 = y2
- ASSUMING α1 = α2 = 1:
- y1 + V12/(2g) + So Δx = y2 + V22/(2g) + hL
- FOR THE SPECIAL CASE WHEN CHANNEL IS HORIZONTAL (So = 0), AND THE HEAD LOSS IS ZERO (hL = 0):
- y1 + V12/(2g) = y2 + V22/(2g)
- THIS MAY BE THE CASE OF A HORIZONTAL AND SHORT CHANNEL.
- SPECIFIC ENERGY:
E = y + V2/(2g)
- THE CONTINUITY EQUATION IS:
- Q = A1V1 = A2V2
- y1 + Q2/(2gA12) = y2 + Q2/(2g A22)
- BECAUSE A = f (y), FOR A GIVEN DISCHARGE, THE SPECIFIC ENERGY IS SOLELY A FUNCTION OF FLOW DEPTH.
- FUNCTION y vs E IS SHOWN BELOW.

|

|
- FOR A GIVEN SPECIFIC ENERGY, THE DEPTH CAN BE LARGE OR SMALL.
- FOR LOW DEPTH, VELOCITY IS HIGH;
- FOR HIGH DEPTH, VELOCITY IS LOW.
- POTENTIAL ENERGY (DEPTH) AND KINETIC ENERGY (VELOCITY).
- FLOW UNDER A SLUICE GATE IS AN EXAMPLE OF FLOW WITH TWO DEPTHS.
- THE LARGE DEPTH AND LOW KINETIC ENERGY OCCURS UPSTREAM OF THE GATE.
- THE LOW DEPTH AND HIGH KINETIC ENERGY OCCURS DOWNSTREAM OF THE SLUICE GATE.
- THE TWO DEPTHS AT WHICH SAME FLOW CAN OCCUR ARE CALLED ALTERNATE DEPTHS.
- IF WE MAINTAIN SAME RATE OF FLOW, BUT SET THE GATE WITH A LARGER OPENING, THE U/S DEPTH WILL DROP AND THE D/S DEPTH WILL RISE.
- THUS, WE HAVE DIFFERENT ALTERNATE DEPTHS AND A SMALLER VALUE OF SPECIFIC ENERGY.
- A POINT IS REACHED WHEN THE SPECIFIC ENERGY IS A MINIMUM, AND ONLY A SINGLE DEPTH OCCURS.
- AT THIS POINT, THE FLOW IS TERMED CRITICAL.
| 090913 |