OPEN CHANNELS III CHAPTER 4 (3) - ROBERSON ET AL., WITH ADDITIONS GRADUALLY VARIED FLOW IN OPEN CHANNELS BASIC DIFFERENTIAL EQUATION FOR GRADUALLY VARIED FLOW: WHEN THE CHANGE IN FLOW DEPTH IS GRADUAL, IT IS POSSIBLE TO INTEGRATE THE RELEVANT DIFFERENTIAL EQUATION. NUMERICAL INTEGRATION IS APPLICABLE. y1 + V12/(2g) + So Δx = y2 + V22/(2g) + Sf Δx Sf = FRICTION SLOPE Δy = y2 - y1 V22/(2g) - V12/(2g) = {d[V2/(2g)]/dx} Δx Δy = So Δx - Sf Δx - {d[V2/(2g)]/dx} Δx FROM WHICH: dy/dx + d[V2/(2g)]/dx = So - Sf dy/dx + d[V2/(2g)]/dy (dy/dx) = So - Sf dy/dx { 1 + d[V2/(2g)]/dy}   = So - Sf dy/dx = (So - Sf ) / { 1 + d[V2/(2g)]/dy } d[V2/(2g)] /dy = d[Q2/(2gA2)] /dy d[V2/(2g)] /dy = - [2Q2/(2gA3)] dA/dy dA/dy = T d[V2/(2g)] /dy = - [Q2/(gA3)] T A/T = D d[V2/(2g)]/dy = -Q2/(gA2D) d[V2/(2g)]/dy = -V2/(gD) = - F2 dy/dx = (So - Sf) / (1 - F2) THE FRICTION SLOPE:  Sf = ScF2 dy/dx = (So - ScF2) / (1 - F2) dy/dx = Sy Sy = (So - ScF2) / (1 - F2) Sy/Sc = [(So/Sc) - F2 / (1 - F2) THIS EQUATION DESCRIBES THE VARIOUS TYPES OF SURFACE PROFILES. CLASSIFICATION OF WATER SURFACE PROFILES: THERE ARE 12 WATER SURFACE PROFILES CLASSES: MILD, STEEP, CRITICAL, HORIZONTAL, ADVERSE. CHARACTERISTICS OF FLOW PROFILES. QUANTITATIVE EVALUATION OF WATER SURFACE PROFILES IN PRACTICE, MOST SURFACE PROFILES ARE GENERATED BY NUMERICAL INTEGRATION, THAT IS, BY DIVIDING THE CHANNEL INTO SHORT REACHES AND CARRYING THE COMPUTATION FOR WATER SURFACE ELEVATION FROM ONE END OF THE REACH TO ANOTHER. METHODS: -- DIRECT STEP METHOD. -- STANDARD STEP METHOD. IN THE DIRECT STEP METHOD, THE DEPTH AND VELOCITY ARE KNOWN AT A GIVEN SECTION, AND ONE ARBITRARILY CHOOSES THE DEPTH AT THE OTHER END OF THE REACH, AND SOLVES FOR THE REACH LENGTH. y1 + V12/(2g) + So Δx = y2 + V22/(2g) + Sf Δx E1 + So Δx = E2 + Sf Δx Δx = (E1 - E2) / ( Sf - So) FIRST ASCERTAIN THE TYPE OF PROFILE (M, C, S, H, A) THEN, STARTING FROM A KNOWN DEPTH, A FINITE VALUE OF Δx IS COMPUTED FOR AN ARBITRARILY CHOSEN CHANGE IN DEPTH. WITH THE AID OF THE COMPUTER, THE Δx INCREMENT CAN BE TAKEN VERY SMALL. PROCESS IS REPEATED UNTIL A FULL LENGTH OF CHANNEL HAS BEEN COVERED. 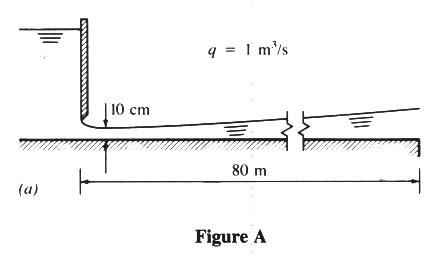THE FRICTION SLOPE IS APPROXIMATED BY THE FOLLOWING: Sf = n2V2 /(1.492 R4/3) Sf = f V2 /(8g R) IN WIDE CHANNELS: D ≅ R Sf = (f/8) V2 /(g D) = (f/8) F2 EXAMPLE 4-10 WATER DISCHARGES FROM UNDER A SLUICE GATE INTO A HORIZONTAL CHANNEL AT THE RATE OF 1 M3/SEC/M AND y = 0.1 M (10 cm). WHAT IS THE TYPE OF W.S. PROFILE? EVALUATE THE PROFILE D/S OF THE GATE AND DETERMINE WHETHER OR NOT IT WILL EXTEND TO THE ABRUPT DROP LOCATED 80 M DOWNSTREAM. THE RESISTANCE FACTOR IS f = 0.02, AND THE HYDRAULIC RADIUS R IS EQUAL TO THE DEPTH y. (WIDE RECTANGULAR CHANNEL) THE CRITICAL DEPTH IN A WIDE RECTANGULAR CHANNEL IS: yc = (q2/g)1/3 = (12/9.81)1/3 = 0.467 M SINCE y < yc, AND THE CHANNEL IS HORIZONTAL, THE PROFILE IS H3. CHOOSE A DEPTH INTERVAL OF 0.04 M DETAILS OF COMPUTATIONAL TABLE SHOWN BELOW. ONLINE CALCULATION OF H3 PROFILE: EXAMPLE OF BOOK: Q = 100; B= 100; z= 0; (assume) Manning's n = 0.013, no. intervals n = 9; no. tabular output intervals m = 9; u/s flow depth = 0.1; u/s bottom slope = 0.4. RESULT: PROFILE REACHES 0.345 M AT 70.46 M. RESULT: PROFILE REACHES 0.467 M AT 88.01 M. COMPARE WITH BOOK TABLE: PROFILE REACHES 0.34 M AT 82.8 M. PROFILE REACHES ABRUPT DROP BEFORE REACHING CRITICAL DEPTH. MORE ACCURATE SOLUTION OF EXAMPLE OF BOOK: Q = 100; B = 100; z = 0; (assume) Manning's n = 0.013, no. intervals n = 100; no. tabular output intervals m = 100; u/s flow depth = 0.1; u/s bottom slope = 0.4. RESULT: PROFILE REACHES 0.339 M AT 72.87 M. RESULT: PROFILE REACHES 0.467 M AT 91.93 M. PROFILE REACHES ABRUPT DROP (80 M) BEFORE REACHING CRITICAL DEPTH. THE DIRECT STEP METHOD IS IDEALLY SUITED TO PRISMATIC CHANNELS, BECAUSE THE CHANNEL CROSS-SECTION IS CONSTANT AND INDEPENDENT OF THE POSITION. IN NONPRISMATIC CHANNELS, CROSS SECTIONS VARY ALONG THE CHANNEL. THE SECTIONS ARE FIXED, AND COMPUTATIONS ARE MADE BETWEEN SECTIONS FOR WHICH DATA IS AVAILABLE. OBJECTIVE IS NOW TO DETERMINE y FOR A GIVEN Δx. THIS IS THE STANDARD STEP METHOD. WE USE ENERGY EQUATION: y1 + V12/(2g) + So Δx = y2 + V22/(2g) + Sf Δx + hc hc = HEAD LOSSES OTHER THAN SURFACE RESISTANCE. THE METHOD OF SOLUTION IS ITERATIVE. ALL INFORMATION IS KNOWN AT SECTION 1. ONE ASSUMES A DEPTH FOR SECTION 2. THEN CALCULATE VELOCITY, FRICTION SLOPE, AND OTHER LOSSES. IF ENERGY EQUATION IS NOT SATISFIED, A NEW VALUE OF DEPTH IS CHOSEN. COMPUTER SOLUTIONS ARE NECESSARY. HEC-RAS DOES THIS COMPUTATION. 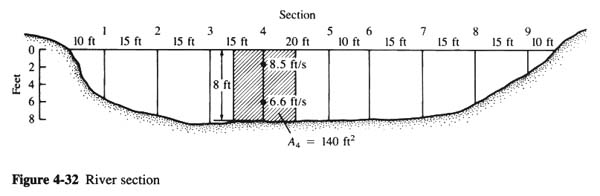MEASUREMENT OF DISCHARGE IN OPEN CHANNELS DISCHARGE Q = VA STANDARD PRACTICE IS TO MAKE VELOCITY MEASUREMENTS AT VARIOUS STATIONS ACROSS THE RIVER, AND TO APPORTION TO EACH STATION THE FLOW-SECTION AREA THAT IS CLOSEST TO THAT PARTICULAR STATION. TOTAL DISCHARGE: Q = ∑ Vi Ai MEAN VELOCITY IS APPROXIMATED BY THE VELOCITY TAKEN AT 0.2 AND 0.8 OF DEPTH BELOW THE SURFACE. FOR SHALLOW DEPTHS, A SINGLE MEASUREMENT AT 0.6 DEPTH MAY SUFFICE. THE MOST COMMON VELOCITY METER IS THE PRICE CURRENT METER. CUPS ON A WHEEL MOUNTED ON A VERTICAL AXIS CAUSE THE WHEEL TO ROTATE WHEN WATER FLOWS PAST IT. WEIRS, FLUMES, SPILLWAYS, AND GATES SHARP-CRESTED WEIRS: A SIMPLE DEVICE FOR DISCHARGE MEASUREMENT IN CANALS AND FLUMES IS THE SHARP-CRESTED WEIR. WHEN ATMOSPHERIC PRESSURE PREVAILS ABOVE AND BELOW THE NAPPE, IT IS SAID TO BE WELL VENTILATED. 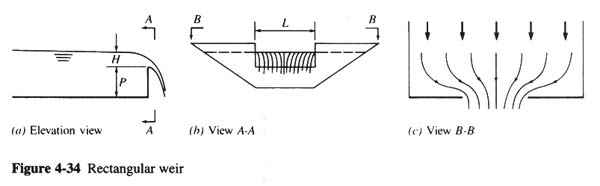THE DISCHARGE EQUATION FOR A RECTANGULAR WEIR (THAT SPANS A RECTANGULAR FLUME) IS: Q = K (2g)1/2 L H3/2 K IS THE WEIR COEFFICIENT K = 0.40 + 0.05 H/P H = head above crest P = height of wall (FIG. 4-34). THIS EQUATION IS VALID UP TO H/P ABOUT 10. OFTEN THE WEIR SECTION DOES NOT SPAN THE ENTIRE WIDTH OF THE CHANNEL. CONTRACTION OF FLOW SECTION FORCES THE EFFECTIVE LENGTH OF THE WEIR TO BE LESS THAN L. EXPERIMENTS SHOW THAT THIS EFFECTIVE REDUCTION IN LENGTH IS APPROXIMATELY EQUAL TO 0.2 H WHEN L/H > 3. FORMULA FOR CONTRACTED WEIR (ONE WITH FLOW CONTRACTION DUE TO END WALLS) IS: Q = K (2g)1/2 (L - 0.2H) H3/2 Chuntacala Creek, Peru. 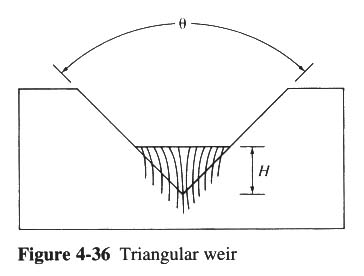WITH LOW FLOW RATES, IT IS COMMON TO USE A TRIANGULAR WEIR. THE BASIC TRIANGULAR WEIR EQUATION IS: Q = (8/15) K (2g)1/2 tan (θ/2) H5/2 K = FLOW COEFFICIENT, PRIMARILY A FUNCTION OF H. FOR θ VALUES BETWEEN 60o AND 90o, K VARIES FROM 0.60 TO 0.57 AS THE HEAD VARIES FROM 0.2 TO 2 FT. BROAD-CRESTED WEIRS: IF THE WEIR IS LONG IN THE DIRECTION OF FLOW, SO THAT THE FLOW LEAVES THE WEIR IN A HORIZONTAL DIRECTION, THE WEIR IS SAID TO BE BROAD-CRESTED. BASIC THEORETICAL EQUATION IS: Q = 0.385 (2g)1/2 L H3/2 Qtheoretical = 0.385 (2g)1/2 L H3/2 Qactual = 0.385 (2g)1/2 C' L H3/2 where C' is an empirical correction coefficient generally taken as less than 1. For instance, for the Boeraserie Conservancy (Guyana) broad-crested weir, for which 1.7 C' = 1.45: C' = 1.45/1.70 = 0.85 Equations with C': Q = 3.09 C' L H3/2     [U.S. CUSTOMARY UNITS] Q = 1.70 C' L H3/2     [SI UNITS] In general, the broad-crested weir equation is: Q = C L H3/2 where C is the discharge coefficient. 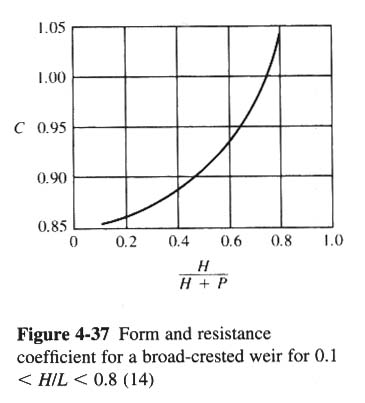(C = 1.7 C'; or C = 3.09 C') LEGACY TALE:   THE DISCHARGE COEFFICIENT. FOR LOW WEIRS, THE VELOCITY OF APPROACH CAN BE SIGNIFICANT, AND THIS EFFECT WILL TEND TO MAKE C' GREATER THAN 1. THE FRICTIONAL RESISTANCE OVER THE LENGTH OF THE WEIR WILL TEND TO MAKE C' LESS THAN 1. FIG. 4-37 SHOWS C' (shown as C in this figure) VARYING FROM 0.85 TO 1.05. THESE ARE FOR A WEIR WITH A VERTICAL U/S FACE AND A SHARP CORNER AT THE INTERSECTION OF THE U/S FACE AND THE WEIR CREST. IF THE U/S IS SLOPING AT 45o, THE C' SHOULD BE INCREASED BY 10%. ROUNDING THE UPSTREAM CORNER WILL PRODUCE AN INCREASE OF 3% IN C'. VENTURI FLUME (PARSHALL FLUME) DISADVANTAGES OF THE BROAD-CRESTED WEIR ARE THAT IT PRODUCES CONSIDERABLE HEAD LOSS, AND SEDIMENT CAN ACCUMULATE IN FRONT OF IT. TO REDUCE BOTH OF THESE DETRIMENTAL EFFECTS, THE VENTURI FLUME WAS DEVELOPED AND CALIBRATED BY PARSHALL. CRITICAL FLOW IS PRODUCED BY REDUCING THE WIDTH OF THE CHANNEL (THE VENTURI EFFECT) AND BY INCREASING THE SLOPE OF THE BOTTOM IN THE CONTRACTED SECTION. THUS, THE CONTRACTED SECTION SERVES AS A CONTROL AND A UNIQUE HEAD-DISCHARGE (STAGE-DISCHARGE) RELATIONSHIP EXISTS IF THE DEPTH DOWNSTREAM OF THE CONTRACTED SECTION IS LOW ENOUGH TO ALLOW "FREE FLOW" THROUGH THE CONTRACTED SECTION. 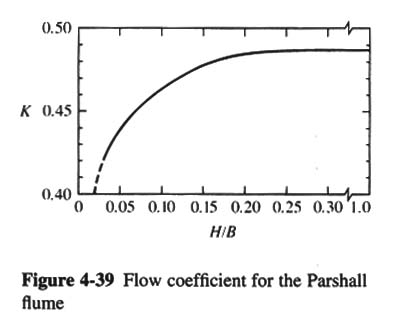FREE FLOW CRITERION BASED ON RATIO TO DOWNSTREAM HEAD TO UPSTREAM HEAD: Hd /Hu < 0.7 Q = K (2g)1/2 W Hu3/2 W = THROAT WIDTH. Hu = HEAD MEASURED AT CONTROL SECTION UPSTREAM OF FLUME K = COEFFICIENT FUNCTION OF Hu/W (FIG. 4-39:   Hu/W = H/B). Parshall flume at Cucuchucho constructed wetland, Michoacan, Mexico. SPILLWAYS THE SPILLWAY ON A DAM SERVES AS THE CONTROL SECTION. THEREFORE, IT CAN BE USED FOR DISCHARGE MEASUREMENTS. GENERAL FORM OF DISCHARGE EQUATION: Q = K (2g)1/2 L H3/2 THE HEAD H IS MEASURED FROM THE CREST OF THE SPILLWAY. THE LENGTH L IS THE LENGTH OF THE SPILLWAY, NORMAL TO THE FLOW. THE VALUE OF THE DISCHARGE COEFFICIENT DEPENDS ON THE SHAPE OF THE SPILLWAY AND THE RATIO OF HEAD TO HEIGHT OF DAM. THE DISCHARGE IS ALSO INFLUENCED BY PIERS THAT SUPORT GATES AND ROADWAY. El Capitan Dam, San Diego County. San Vicente Dam, San Diego County. Morena Dam, San Diego County. Hodges Dam, San Diego County. Turner Dam, San Diego County. Oroville Dam, California. Gallito Ciego Dam, Peru. Villa Grande Dam, Peru. Mangla Dam, Pakistan. LABYRINTH SPILLWAY SEEKS TO INCREASE Q BY INCREASING EFFECTIVE L. Ute Dam, New Mexico. Valentine Mill Pond, Nebraska.     Melaka, Malaysia. SLUICE AND TAINTER GATES SLUICE AND TAINTER GATES ARE USED EXTENSIVELY FOR CONTROLLING WATER IN CANALS, IN FLUMES, AND ON SPILLWAYS. THEY FALL IN THE CATEGORY OF UNDERFLOW GATES. Cresta Dam, North Fork Feather River, California. 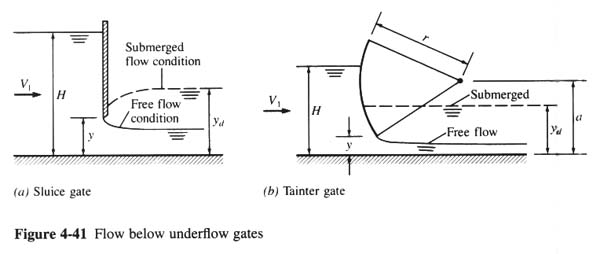THE DISCHARGE THROUGH UNDERFLOW GATES IS: Q = CcCv L y (2g)1/2 [H + V12/(2g) - Ccy]1/2 Cc = contraction coefficient, a function of the relative gate opening and the shape of the gate Cv = velocity coefficient, with a value slightly less than 1. y = gate opening. V1 = approach velocity. FOR CONVENIENCE, THIS EQUATION IS SIMPLIFIED TO: Q = K L y (2gH)1/2 K IS A FLOW COEFFICIENT THAT IS A FUNCTION OF THE SAME PARAMETERS AS Cc. 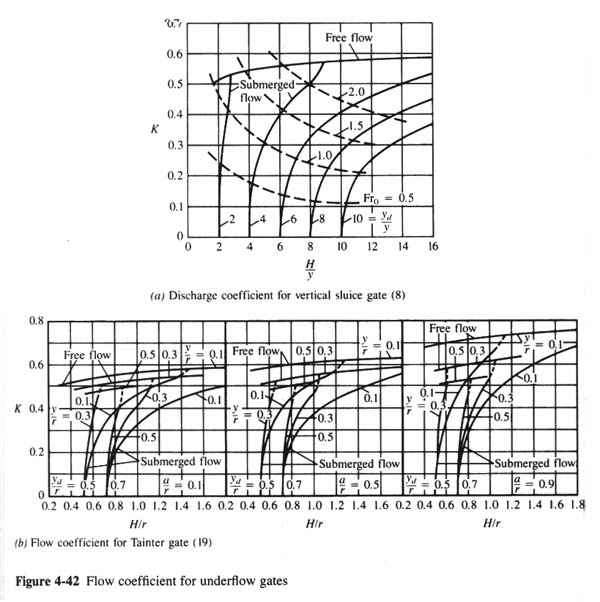IF THE DOWNSTREAM JET IS SUBMERGED, THE DISCHARGE IS ALSO A FUNCTION OF THE DOWNSTREAM DEPTH yd (FIG. 4-42). IN FIG. 4-42, Fro is the Froude number based on the gate opening (V and y). THEORETICAL VALUE OF SLUICE GATE DISCHARGE (ENERGY BALANCE): ASSUME CONSTANT SPECIFIC ENERGY (NO FRICTION LOSSES): [V12/(2g)] + y1 = [V22/(2g)] + y2 q2/[(y12(2g)] + y1 = q2/[(y22(2g)] + y2 [q 2/(2g)] [1/y12 - 1/y22] = y2 - y1 [q 2/(2g)] [1/(y12 y22)] = 1/(y1 + y2) q = (2g)1/2 y1 y2 /(y1 + y2)1/2 H = y1 y = y2 q = Q/L = (2g)1/2 (yH) / (H + y)1/2 H = y1 = 1 m. y = y2 = 0.1 m. RESULT [http://ponce.sdsu.edu/onlinechannel13.php]: q = Q/L = 0.422 m3/s/m COMPARE WITH PRACTICAL FORMULA: K = 0.575 [FOR H/y = 10, FREE FLOW, FROM FIG. 4-42] q = Q/L = 0.575 × 0.1 (2 × 9.81 × 1)1/2 = 0.255 m3/s/m Poechos Dam, Peru. Tarbela Dam, Pakistan. Oroville Dam, California. Itaipu Dam, Brazil. Tucurui Dam, Brazil. Close view of Morning Glory spillway, on the Barragem Norte cofferdam site, Itajai river, in Santa Catarina, Brazil. The spillway got plugged with vegetative debris (visible on the left side) during a flood event in December 1982, and led to the breach of the temporary structure. Morning Glory spillway, Barragem Norte, Brazil. Morning Glory spillway for Monticello Dam, California. Morning Glory spillway for Monticello Dam, California. Monticello Dam, California, showing Morning Glory spillway near right abutment. 091012