CHAPTER 5 (1) -- ROBERSON ET AL., WITH ADDITIONS
-- HEAD LOSSES (LINE AND LOCAL)
-- FORCES (CHANGES IN MOMENTUM) AND STRESSES ON THE PIPE
MATERIAL
-- DISCHARGE
PIPE FLOW

|
Orange County Sanitation District's ocean outfall pipeline,
Huntington Beach, California.
- FORCES AND STRESSES RESULT FROM FLUID PRESSURE.
- FORCES ARE CREATED BY MOMENTUM CHANGE FOR FLOW AROUND BENDS.
- CONTINUITY, ENERGY, AND MOMENTUM EQUATIONS ARE USED IN CLOSED CONDUIT FLOW.
- TO DESIGN A PIPE:
-- USE CONTINUITY AND ENERGY EQUATIONS TO DESIGN PIPE DIAMETER.
-- USE MOMENTUM EQUATION TO CALCULATE FORCES ACTING ON BENDS FOR A GIVEN DISCHARGE.
-
ENERGY EQUATION
- INITIAL DESIGN INVOLVES DETERMINING SIZE OF CONDUIT WITH THE LEAST COST FOR THE GIVEN DISCHARGE.
|
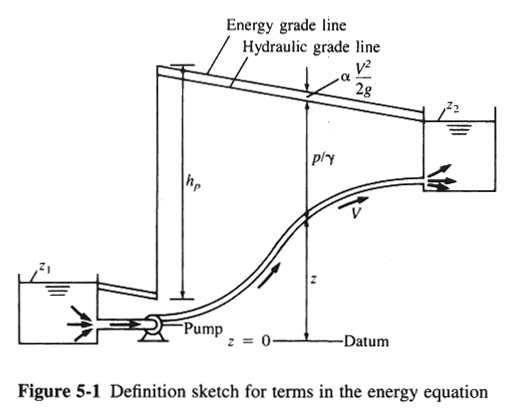
- THE ENERGY EQUATION IS:
- p1/γ + α1V12/(2g) + z1 + hp =
p2/γ + α2V22/(2g) + z2 + hL
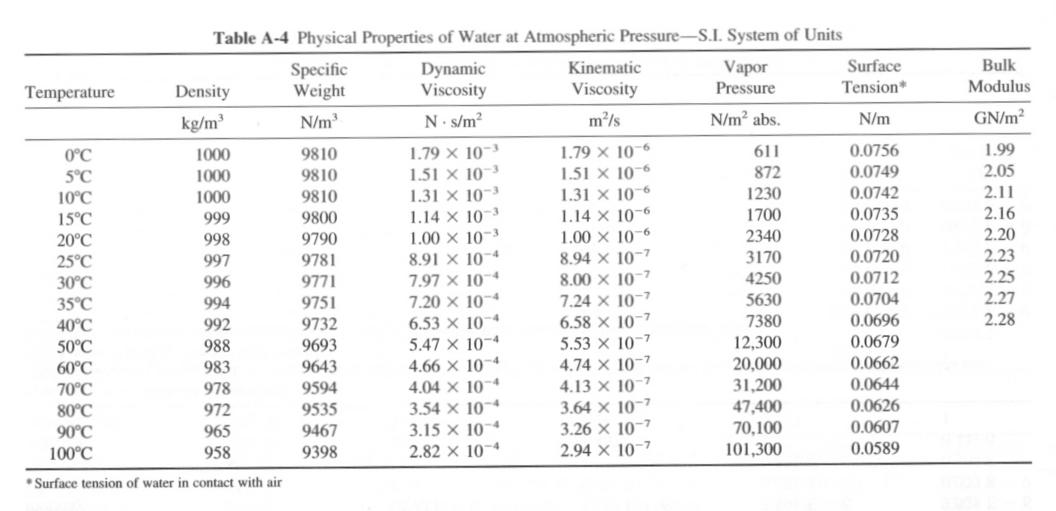
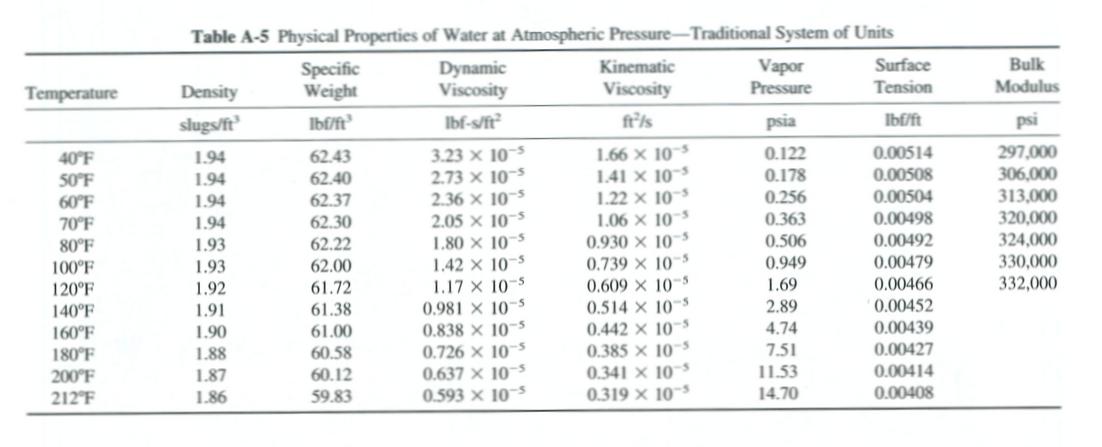
p1/γ = pressure head at point 1
αV12/(2g) = velocity head at point 1
z1 = elevation (head) at point 1
hp = head supplied by a pump
p2/γ = pressure head at point 2
αV22/(2g) = velocity head at point 2
z2 = elevation (head) at point 2
hL = head loss between points 1 and 2
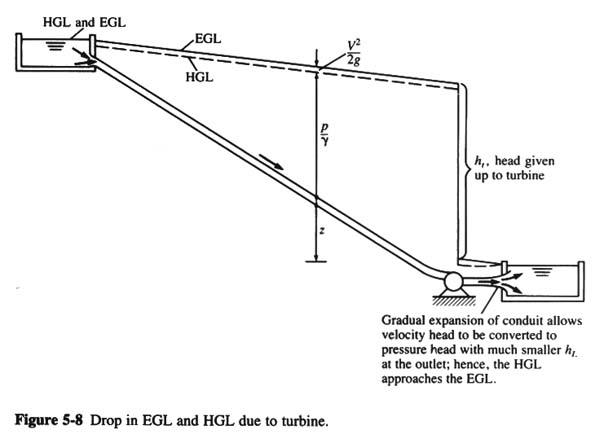
ht = head supplied to a turbine
- p1/γ + α1V12/(2g) + z1 =
p2/γ + α2V22/(2g) + z2 + ht + hL
|

|
Calleguas Brine Line under construction, Port Hueneme, California.

|
Pelton turbine.
- IT IS OBTAINED FROM Q AND A (V = Q/A), WHERE A IS THE CROSS-SECTIONAL AREA OF THE PIPE, BASED ON THE DIAMETER.
- α = 1 WHEN THE VELOCITY IS UNIFORM ACROSS THE SECTION.
- IN LAMINAR FLOW, α HAS A VALUE OF 2.
- IN TURBULENT FLOW, α HAS A VALUE CLOSE TO 1 (1.04 < α < 1.06).
- IN HYDRAULIC ENGINEERING, α IS ASSUMED TO BE 1.
VELOCITY HEAD
-
PUMP OR TURBINE HEAD
- HEAD SUPPLIED BY PUMP [OR DELIVERED TO TURBINE]
IS DIRECTLY RELATED TO THE POWER P
SUPPLIED TO [OR TAKEN FROM] THE FLOW:
P = γ Q hp
P = γ Q ht
- IN PRACTICE, NOT ALL THE POWER IS REALIZED. SYSTEM LOSSES MAKE IT NECESSARY TO INCLUDE AN EFFICIENCY FACTOR e:
- P = e γ Q ht
- POWER = ENERGY/TIME = (FORCE × LENGTH) / TIME
- P (N × M / SEC) = γ [N/M3] Q [M3/S] ht [M]
- 1 N × M = 1 JOULE
- 1 N × M / S = 1 WATT
- SI UNITS: POWER IS MEASURED IN WATTS.
- A DISCHARGE Q = 10 M3/S AND A FALL ht = 5 M WILL CREATE A POWER OF:
- P = 9810 (N/M3) × 10 (M3/S ) × 5 (M) =
- P = 490,500 W = 490.5 KW
- A DISCHARGE OF 1 M3/S AND A FALL OF 1 M WILL CREATE A POWER OF:
- P = 9810 (N/M3) × 1 (M3/S ) × 1 (M) =
- P = 9810 W = 9.81 KW
- CONSIDERING EFFICIENCY (LOSSES):
- P ≅ 8 KW
- RULE-OF-THUMB:
- P (KW) = 8 Q (M3/S) h (M)
- IN U.S. CUSTOMARY UNITS:
- P (FT ⋅ LB/S) = γ (LB/FT3) × Q (FT3/S) × ht (FT)
- U.S. UNITS: POWER IS MEASURED IN HP (HORSEPOWER).
- 1 HP = 550 FT ⋅ LB/S
- A DISCHARGE Q = 10 M3/S = 353.15 FT3/S AND A FALL ht = 5 M = 16.404 FT WILL CREATE A POWER OF:
- P = 62.4 (LB/FT3) × 353.15 (FT3/S ) × 16.404 (FT) =
- P = 361,488 FT ⋅ LB/S = 361,488 / (550) = 657.2 HP
- THEREFORE: 657.2 HP = 490.5 KW
- THUS: 1 HP = 0.746 KW
-
HEAD LOSS UNDER LAMINAR FLOW
- THE HEAD LOSS ACCOUNTS FOR THE CONVERSION OF MECHANICAL ENERGY TO INTERNAL (HEAT) ENERGY, WHICH IS LOST.
- HEAD LOSS RESULTS FROM VISCOUS RESISTANCE TO FLOW, OR FROM VISCOUS DISSIPATION OF TURBULENCE IN SEPARATED FLOW.
- IN LAMINAR FLOW, THE HEAD LOSS IS DUE TO VISCOUS RESISTANCE.
- IN THIS CASE, THE HEAD LOSS IS A FUNCTION OF THE FIRST POWER OF THE VELOCITY.
- IN TURBULENT FLOW, THE HEAD LOSS IS
RELATED TO THE DISSIPATION OF THE
KINETIC ENERGY OF TURBULENCE.
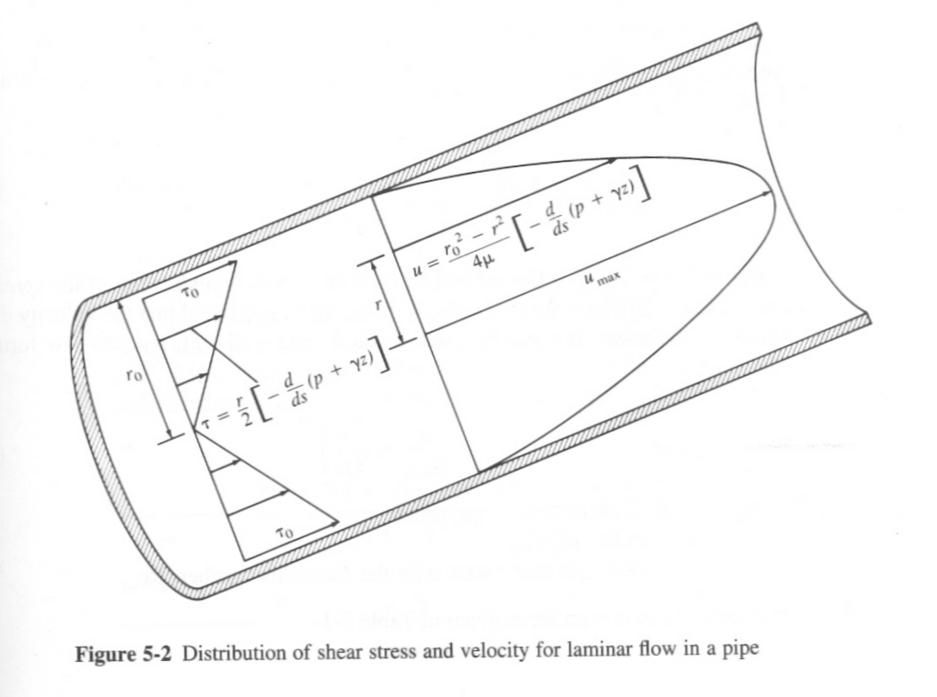
- HEAD LOSS FOR LAMINAR FLOW (INTEGRATING THE VELOCITY DISTRIBUTION ACROSS THE CROSS SECTION):
- hL= 32 μ L V / (γ D2)
- UNITS FOR HEAD LOSS: [(N*S/M2) (M) (M/S)] / [(N/M3) (M2)] = M
- ENERGY GRADELINE: hL/L = 32 μ V / (γ D2)
- μ = ρ ν
- γ = ρ g
- hL/L = 32 ν V / (g D2)
- hL/L = 32 [ν/(V D)] [V2 / (gD)]
- REYNOLDS NUMBER (BASED ON PIPE DIAMETER): Re = V D/ ν
- hL/L = (32 /Re) [V2 / (gD)]
- FROUDE NUMBER (BASED ON PIPE DIAMETER): (Fr) = V2 / (gD)
- Sf = (32 /Re) (Fr)2
- Sf = f (Fr)2
- IN LAMINAR PIPE FLOW, THE FRICTION COEFFICIENT f IS INVERSELY PROPORTIONAL TO THE REYNOLDS NUMBER.
- SINCE DISCHARGE Q = V A = V π (D2/4)
- V = 4Q / (πD2)
- hL = 128 μ L Q / (γ π D4)
- μ = ρ ν
- γ = ρ g
- hL = 128 ν L Q / (g π D4)
- LOSSES ARE SEEN TO VARY DIRECTLY WITH VISCOSITY, LENGTH, AND DISCHARGE, AND INVERSELY WITH THE FOURTH POWER OF THE DIAMETER.
- LESSER DIAMETER MEANS MORE LOSSES.
- TUBE ROUGHNESS DOES NOT ENTER INTO THE EQUATIONS FOR LAMINAR FLOW IN PIPE.
- Q = g hL π D4/(128 ν L)
- HAGEN-POISEUILLE EQUATION FOR PIPE DISCHARGE UNDER LAMINAR FLOW:
- Q = γ hL π D4/(128 μ L)
- UNITS: M3/S = (N/M3) (M) (M4) / [(N*S/M2) (M)]
-
HEAD LOSSES IN TURBULENT FLOW
- SMOOTH PIPES:
- FLOW IS TURBULENT WHEN REYNOLDS NUMBER: Re = VD/ν = VDρ/μ > 3000
- THE SHEAR STRESS IS PRIMARILY IN THE FORM OF REYNOLDS STRESSES, ARISING FROM TURBULENT VELOCITY FLUCTUATIONS.
- REYNOLDS STRESSES VARY LINEARLY FROM ZERO AT THE CENTER OF THE PIPE, OUTWARDS.
- NEAR THE WALL, IN THE VISCOUS SUBLAYER, REYNOLDS STRESSES DECREASE, AND A TRUE VISCOUS SHEAR STRESS TAKES OVER.
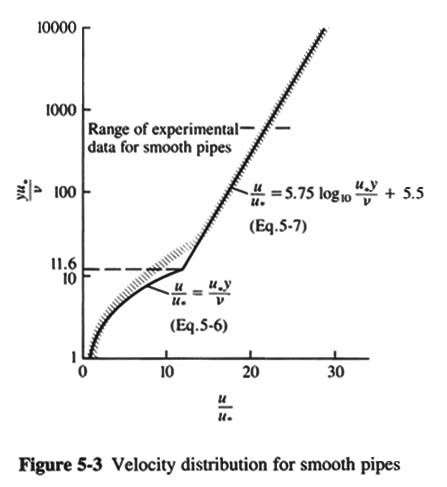
- IN THE VISCOUS SUBLAYER:
-
u / u* = u* y /ν
for: 0 < u* y /ν < 10
y = distance from pipe wall
ν = kinematic viscosity
- u* = shear velocity = (τo/ρ)1/2
UNITS: (N/M2)/(N*S2/M4) = M/S
- τo = shear stress at pipe wall
- IMMEDIATELY OUTSIDE THE VISCOUS SUBLAYER, THE VELOCITY DISTRIBUTION IS OF LOGARITHMIC FORM:
-
u / u* = 5.75 log10 (u* y /ν) + 5.5
for 20 < u* y / ν < 10000
|
- VELOCITY DISTRIBUTION FOR TURBULENT FLOW CAN BE APPROXIMATED QUITE WELL BY A POWER LAW FORMULA:
- u / umax = (y/ro) m
- umax = velocity at pipe center
- ro = radius of pipe
- m = exponent that varies with the Reynolds number (TABLE 5-1)
TABLE 5-1 EXPONENTS FOR POWER LAW EQUATION
| Re | 4 × 103 | 2.3 × 104 | 1.1 × 105 | 1.1 × 106 | 3.2 × 106
| m | 1/6 | 1/6.6 | 1/7.0 | 1/8.8 | 1/10
| | |||||
-
HEAD LOSS FOR TURBULENT FLOW IN PIPES:
DARCY-WEISBACH FORMULA
- hf = f (L/D) V2/(2g)
- UNITS: (M/M) (M/S)2 / (M/S2) = M
Derivation of Darcy-Weisbach formula
Pressure has dimensions of energy per unit volume, therefore the pressure drop between two points must be proportional to (1/2)ρV2, which has the same dimensions, as it resembles the expression for the kinetic energy per unit volume. We also know that pressure must be proportional to the length L of the pipe between the two points, as the pressure drop per unit length is a constant. To turn the relationship into a proportionality coefficient of dimensionless quantity, we can divide by the hydraulic diameter of the pipe, D, which is also constant along the pipe. Δp ∝ (1/2) ρ V2
γ Δh ∝ (1/2) ρ V2
Δh = (1/2) f (L/D) V2 / g
Δh = f (L/D) V2 / (2g)
- LAMINAR FLOW HEAD LOSS = 32 μ LV/(γD2)
- LAMINAR FLOW HEAD LOSS = 32 ν LV/(gD2)
- TURBULENT FLOW HEAD LOSS = (f/2) LV2/(gD)
- IF f IS PROPORTIONAL TO THE RECIPROCAL OF THE REYNOLDS NUMBER (LAMINAR FLOW):
- f ∝ [1/(Re)]
- f = 64/ Re = 64 / [(VD)/ν)] = 64 ν/(VD)
- REPLACING IN DARCY-WEISBACH FORMULA:
- LAMINAR FLOW HEAD LOSS = 32 ν LV/(gD2) OK!
- THEREFORE, IN LAMINAR FLOW f IS NOT A CONSTANT.
- IN TURBULENT FLOW, THE EXPONENT OF REYNOLDS NUMBER DECREASES TO ZERO.
- FULLY DEVELOPED ROUGH TURBULENT FLOW:
- DARCY-WEISBACH f IS INDEPENDENT OF THE REYNOLDS NUMBER.
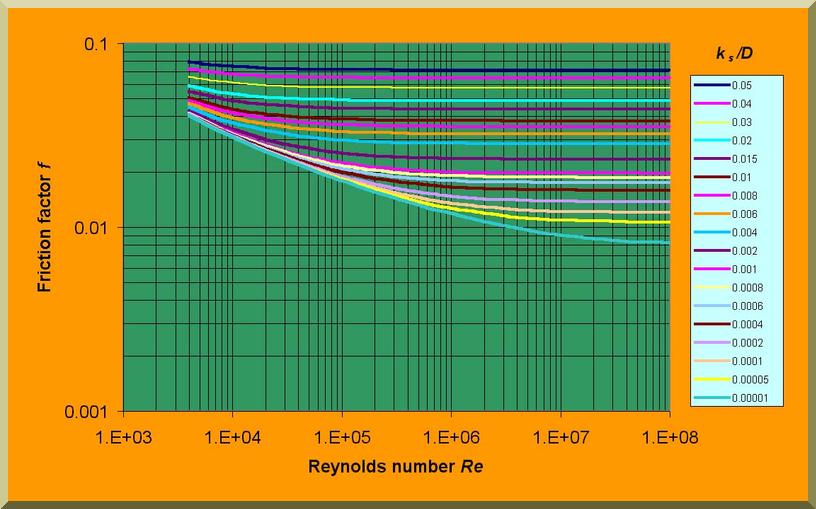
- NIKURADSE DATA JUSTIFIES FORMULA FOR TURBULENT FLOW IN ROUGH PIPES:
- u / u* = 5.75 log10 (y /ks) + 8.5
- y = distance from the geometric mean of the wall surface
- ks = size of sand grains
- THE UNIFORM CHARACTER OF SANDS GRAINS USED BY NIKURADSE PRODUCES A DIP IN THE f vs Re RELATION, BEFORE REACHING A CONSTANT VALUE OF f.
- TESTS IN COMMERCIAL PIPES BY MOODY REVEAL NO SUCH DIP.
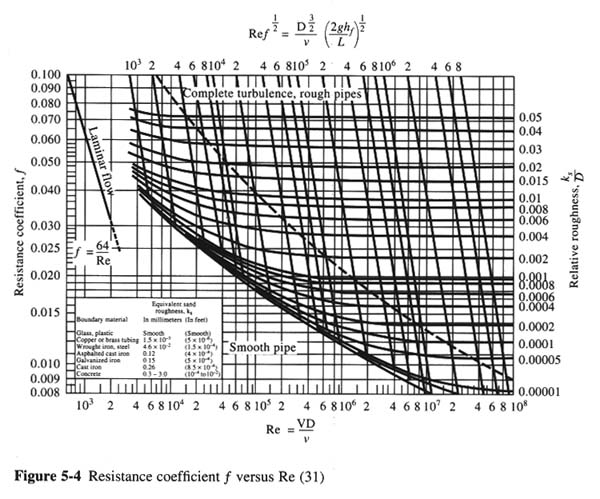
- IN MOODY DIAGRAM ks = equivalent sand roughness; D = pipe diameter
|
Moody diagram for fully developed turbulent flow in pipes.
- FOR CERTAIN PROBLEMS, THE DARCY-WEISBACH EQUATION IS EXPRESSED AS FOLLOWS:
- hf = f (L/D) V2/(2g)
- f = (2 g hf /L) (D/V2)
- f1/2 = (2 g hf D/L)1/2 (1/V)
- f 1/2 Re = (2 g hf D/L)1/2 (1/V) (VD/ν)
- f 1/2 Re = (D3/2/ ν) (2 g hf /L) 1/2
- UNITS: [(M3/2/ (M2/S)] [(M/S2) (M/M)]1/2 DIMENSIONLESS
- DARCY-WEISBACH FORMULA IS APPLICABLE TO ANY FLUID AND ANY SYSTEM OF UNITS.
-
PROBLEMS
1. GIVEN KIND AND SIZE OF PIPE, AND FLOW RATE, DETERMINE THE HEAD LOSS.
2. GIVEN HEAD, KIND AND SIZE OF PIPE, DETERMINE THE FLOW RATE.
3. GIVEN FLOW RATE, KIND OF PIPE, AND HEAD, DETERMINE THE SIZE OF PIPE.
| Type of pipe problem | Q | hf | D | ks
| | X | |
| X | | |
| | | X |
| |
|
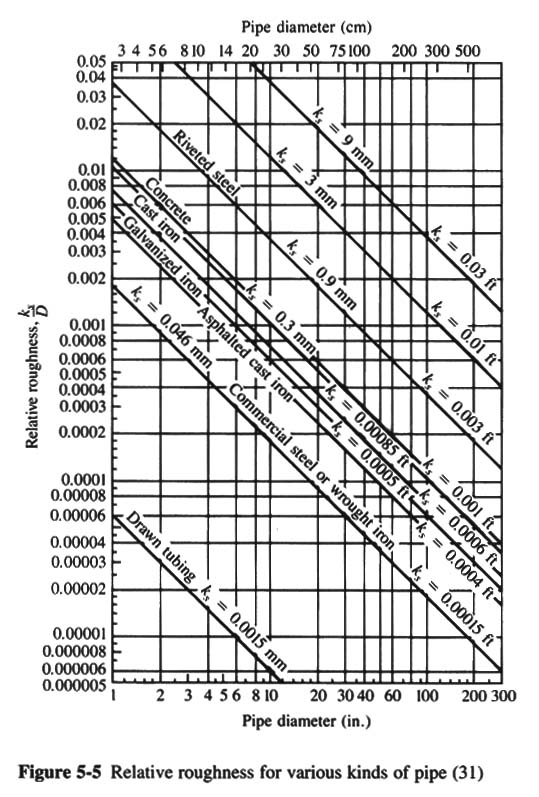
- Q = 0.05 M3/S; T = 20oC; D = 0.2 M, ASPHALTED CAST-IRON PIPE; FIND hf/L (M/KM)
- SOLUTION:
- L = 1000 M
- VELOCITY: V = Q /[(π/4) D2] = 1.59 M/S
- ν = 1.0 X 10-6 M2/S
- Re = VD/ν = 318,000
- FROM FIG. 5-5: ks / D = 0.00065
- FROM FIG. 5-4: f = 0.018
- THEN: hf = f (1000/D) V2/(2g) = 11.6 M
|
|
PROBLEM 1 EXAMPLE
|
-
PROBLEM 2 EXAMPLE
- hf/L = 0.0116; T = 20oC; D = 0.2 M; ASPHALTED CAST-IRON PIPE; FIND Q (M3/S):
SOLUTION:
- ν = 1.0 X 10-6 M2/S
- FROM FIG. 5-5: ks / D = 0.00065
- f 1/2 Re = (D3/2/ν) (2ghf /L)1/2 = [0.23/2 /(1.0 X 10-6) ] [(2) (9.81) (0.0116)]1/2 = 42,670
- FROM FIG. 5-4: f = 0.019
- V = [ (hf/L) 2gD / f ]1/2 = [(0.0116) (2) (9.81) (0.2) / 0.019]1/2 = 1.55 M/S
- Q = VA = V (π/4) D2 = 1.55 (3.1416/4) (0.2)2 = 0.049 ≅ 0.05 M3/S.
- MANY TYPE 2 PROBLEMS CANNOT BE SOLVED DIRECTLY.
- FOR EXAMPLE, WATER FLOWING FROM A RESERVOIR INTO A PIPE AND INTO THE ATMOSPHERE.
- PART OF THE AVAILABLE ENERGY REMAINS IN KINETIC ENERGY AS THE FLOW LEAVES THE PIPE.
- TO GET A SOLUTION, ONE MUST ITERATE ON f.
- CONVERGENCE IS BECAUSE f CHANGES MORE SLOWLY THAN Re.
-
PROBLEM 3 EXAMPLE
- Q = 0.05 M3/S; T = 20o; ASPHALTED CAST-IRON PIPE; hf/L = 0.0116; FIND D.
- SOLUTION:
- ν = 1.0 X 10-6 M2/S
- FIRST ASSUME f = 0.015
- hf = f (L/D) V2/(2g)
- hf = f (L/D) (Q/A)2/(2g)
- hf = f (L/D) [Q/(πD2/4)]2/(2g)
- D5 = f Q2/[(π/4)2(2g) (hf/L)] =
- D5 = 0.015 (0.05)2 / [(0.6169)(2)(9.81)(0.0116)] = 0.015 × 0.0178 = 0.000267
- D = 0.193 M
- NOW COMPUTE A MORE ACCURATE f :
- ks / D = 0.00065
- V = Q/A = 0.05 /[(3.1416/4) (0.193)2] = 1.709 M/S
- Re = VD/ν = 1.709 (0.193) /(1.0 × 10-6 ) = 329,837
- FROM FIG. 5-4: f = 0.0185
- NOW, RECOMPUTE DIAMETER:
- Dnew5 / fnew = Dold5 / fold
- Dnew = [(0.193)5 (0.0185/0.015) ] 1/5 = 0.201 ≅ 0.2 M. OK!
-
HAZEN-WILLIAMS FORMULA
- HAZEN-WILLIAMS FORMULA: EMPIRICAL EQUATION IN U.S. UNITS USED BY WATERWORKS ENGINEERS
- V = 1.318 Ch R 0.63 S 0.54
- V = mean velocity (fps)
- Ch = Hazen-Williams friction coefficient (depends on pipe roughness).
- R = hydraulic radius (ft)
- S = slope of energy gradeline (ft/ft)

|

|
- CHEZY EQUATION:
- V = C R 0.5 S 0.5
- MANNING EQUATION:
- V = (1/n) R 0.67 S 0.5
- THE HAZEN-WILLIAMS FORMULA IS ACCURATE WITHIN A CERTAIN RANGE OF DIAMETERS AND FRICTION SLOPES.
- IT IS USED INDISCRIMINATELY IN PIPE DESIGN.
- IT MAY BE INACCURATE FOR FLUIDS OTHER THAN WATER AND FOR PIPE DIAMETERS SMALLER THAN 2 IN AND LARGER THAN 6 FT.
- TO SOLVE FOR HEAD LOSS WITH HAZEN- WILLIAMS: (R = D/4)
- V = 1.318 Ch R 0.63 (hf/L) 0.54
- (hf/L) 0.54 = (V/Ch) (D/4)-0.63 (1.318)-1
- hf = L [(V/Ch) (D/4)-0.63 (1.318)-1] 1.852
- hf = L (V/Ch ) 1.852 [(D/4)-0.63 (1.318)-1] 1.852
- hf = L D -1.167 (V/Ch ) 1.852 [(1/4) -0.63 (1.318) -1] 1.852
- hf = 3.022 L D -1.167 (V/Ch ) 1.852
- TO SOLVE FOR DISCHARGE WITH HAZEN-WILLIAMS:
- V= Q/A
- A = (π/4)D2
- R = D/4
- V = Q/A = 1.318 Ch (D/4) 0.63 S 0.54
- Q = 1.318 Ch (D/4) 0.63 S 0.54 (π/4) D2
- Q = 1.318 Ch D 2.63 S 0.54 (π/4)(1/4) 0.63
- Q = 0.432 Ch D 2.63 S 0.54
- ONLINE HAZEN-WILLIAMS
- D = 1 ft, S = 0.001.
- Assume C = 130 (AS FOR FIG. 5-6):
- Q = 1.347 CFS.

|
Orange County Sanitation District's ocean outfall pipeline,
Huntington Beach, California.
-
HEAD LOSS IN NONCIRCULAR CONDUITS
- IN DARCY-WEISBACH FORMULA:
- hf = f (L/D) V2/(2g)
- HYDRAULIC RADIUS R = A/P
- IN CIRCULAR PIPE FLOWING FULL:
- R = [(π/4)]D2/ (πD) = D/4
- THEREFORE, THE DARCY-WEISBACH FORMULA IN TERMS OF HYDRAULIC RADIUS IS:
- hf = f/4 (L/R) V2/(2g)
- USE THIS FORMULA FOR NONCIRCULAR PIPES:
- WITH RELATIVE ROUGHNESS ks/(4R) and
- Re = V (4R)/ν
- ALSO, NOTE THAT
- hf/L = [f/(8g)] (1/R) V2
- V = (8g/f) 0.5 R 0.5 (hf/L) 0.5
- V = (8g/f) 0.5 R 0.5 Sf 0.5
- THIS LOOKS LIKE THE CHEZY EQUATION!
- DARCY-WEISBACH EQUATION IS A DIMENSIONLESS CHEZY EQUATION.
- C = (8g/f) 0.5
- C2 = 8g/f
- f/8 = g/C2
- DARCY-WEISBACH: f = 8g/C2
|
-
EXAMPLE 5-3
- A CONCRETE-LINED TUNNEL DESIGNED FOR A DISCHARGE OF 4,300 CFS HAS A CROSS- SECTION DESCRIBED AS FOLLOWS. THE TOP PART IS A 20-FT DIAMETER SEMICIRCLE; THE BOTTOM PART IS RECTANGULAR, 20 FT WIDE BY 10 FT HIGH. ESTIMATE THE HEAD LOSS IN FT/MI. ASSUME ROUGH CONCRETE LINING ks = 0.01 FT.

|
- A = [(π102/2) + (20) (10) ] = 357
- P = [20 + (10)(2) + π 10] = 71.4
- V = Q / A = 4,300 / 357 = 12.05 FT/SEC
- THE HYDRAULIC RADIUS IS: R = A/P = = 357/71.4 = 5 FT.
- TEMP= 60oF
- THE REYNOLDS NUMBER IS:
- Re= V (4R) /ν = (12) (4) (5) / (1.22 × 10 -5)
- Re = 19,672,131
- ROUGHNESS ks = 0.01 ft (rough concrete lining)
- RELATIVE ROUGHNESS ks / (4R) = 0.0005
- FROM MOODY DIAGRAM, WITH Re and ks/(4R), WE OBTAIN:
- f = 0.017
- THE HEAD LOSS PER MILE IS:
- hf = f (L/4R) V2/(2g)
- hf = 0.017 (5280 FT/MI / 20) 12.052/[(2) (32.17)] = 10.12 FT/MI
SOLUTION:
-
HEAD LOSS DUE TO TRANSITIONS AND FITTINGS
- OTHER LOSSES ARE CAUSED BY THE INLET, OUTLET, BENDS, ETC., THAT ALTER THE UNIFORM FLOW REGIME.
- ADDITIONAL TURBULENCE IS CREATED BY THE FITTINGS.
- ENERGY CREATED BY THE TURBULENCE IS DISSIPATED INTO HEAT.
- HEAD LOSS IS EXPRESSED AS:
- hL= K V2/(2g)
- K IS THE LOSS COEFFICIENT FOR THE FITTING.
-
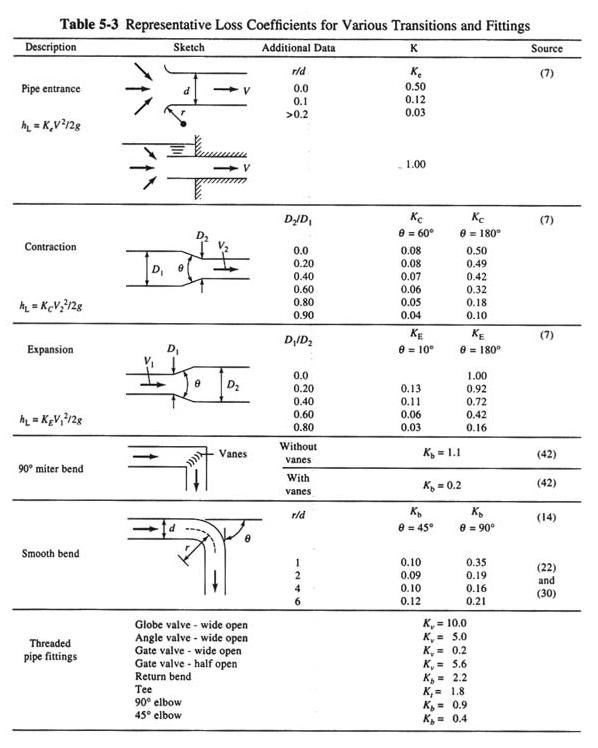
EXAMPLE 5-4
- THE MEAN VELOCITY IS V = 12.05 FPS.
- ASSUME HEAD LOSS FOR GATE VALVE IS NEGLIGIBLE.
- SOLUTION:
- WRITE THE ENERGY EQUATION BETWEEN RESERVOIRS 1 AND 2:
- THE ENERGY DIFFERENCE GOES TO TOTAL HEAD LOSSES PLUS HEAD DELIVERED TO TURBINE.
- THE LINE LOSSES ARE: 10.12 FT/MI X 5 MI = 50.6 FT.
- hL = 50.6 + [V2/(2g)] [ 2Kb + Ke + KE + Kt]
- hL = 50.6 + [12.052/(64.34)] [ 2(0.1) + 0.12 + 0.15 + 0.2]
- KE IS ESTIMATED ASSUMING θ = 10o
- BEND (b), ENTRANCE (e) AND EXIT (E) LOSS COEFFICIENTS FROM TABLE 5-3.
THE CONDUIT OF THE PREVIOUS EXAMPLE IS USED TO CONVEY WATER FROM A RESERVOIR AT ELEVATION 5000 FT, THROUGH TURBINES, AND THEN TO ANOTHER RESERVOIR AT ELEVATION 3000 FT.
THE TUNNEL IS 5 MI LONG AND HAS TWO LONG-RADIUS 45 DEGREE BENDS, with KB = 0.1, PLUS TWO WIDE-OPEN GATE VALVES, AND LOSS COEFFICIENTS FOR INLET Ke = 0.12, AND OUTLET KE = 0.15.
WHAT MAXIMUM POWER (KW) CAN BE DELIVERED TO THE TURBINES, ASSUMING THE FLOW PASSAGE ASSOCIATED WITH THE TURBINES RESULTS IN A LOSS COEFFICIENT OF 0.2 OF VELOCITY HEAD?
|
- hL = 50.6 + 1.5 = 52.1 FT
- THE HEAD DELIVERED TO TURBINES IS THEN:
- ht = 5000 - 3000 - 52.1 = 1947.9 FT.
- THE MAXIMUM POWER THAT COULD BE DELIVERED TO THE TURBINES IS:
- P (FT ⋅ LB/S) = γ (LB/FT3) Q (FT3/S) ht (FT)
- 1 HP = 550 FT ⋅ LB/SEC
- P (HP) = 62.4 (LB/FT3) 4300 (FT3/S) 1947.9 (FT) / 550
- P (HP) = 950,292 HP
- 1 HP = 0.746 KW
- P (KW) = 708,918 KW
- P (MW) = 708.9 MW
| 160304 17:30 |