HYDRAULIC MACHINERY CHAPTER 8 - ROBERSON ET AL., WITH ADDITIONS DIMENSIONLESS PARAMETERS FOR TURBO MACHINES n = speed of rotation D = diameter of pump impeller ρ = mass density of fluid being pumped g = gravitational acceleration P = Power supplied to pump ΔH = change in head (head increase) produced by pump HEAD COEFFICIENT CH = ΔH / (D2n2 / g) UNITS:   L/[L2T-2/(L/T2)] POWER COEFFICIENT CP= P / (ρD5n3) UNITS:   (LF/T)/[(FT2/L4)L5T-3] DISCHARGE COEFFICIENT CQ = Q / (nD3) UNITS:   (L3/T)/[T-1L3] CH AND CP ARE FUNCTIONS OF CQ FOR A GIVEN TYPE OF PUMP. AXIAL FLOW PUMPS FIG. 8-5 IS A SET OF CURVES OF CH, CP, n, VS. CQ. FIG. 8-6 SHOWS HEAD, POWER, AND EFFICIENCY VS DISCHARGE. 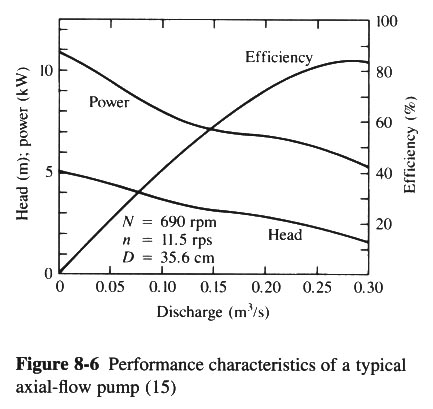THESE ARE CHARACTERISTIC OR PERFORMANCE CURVES. EXAMPLE 8-1 FOR THE PUMP REPRESENTED BY FIGS. 8-5 AND 8-6, WHAT DISCHARGE WILL OCCUR WHEN THE PUMP IS OPERATING AGAINST A 2 m HEAD AT A SPEED OF 600 RPM? WHAT POWER IN KW IS REQUIRED FOR THESE CONDITIONS? SOLUTION: FROM FIG. 8-6:   D = 35.6 cm = 0.356 m n = 600 rpm = 10 rps CH = ΔH / (D2n2 / g) = CH = 2 (9.81) / [(0.3562)(102)] = 1.55 FROM FIG. 8-5, FOR CH = 1.55:  CQ = 0.38 CQ = Q / (nD3) 0.38 = Q / [(10)(0.3563)] Q = 0.171 m3/s FROM FIG 8-5, FOR CQ = 0.38:   CP = 0.80 CP = P / (ρD5n3) P = CP ρD5n3 P = 0.80 (1 KNs2/m4) (0.3565 m5) (103 s-3) P = 4.57 KN m/s P = 4.57 KW EXAMPLE 8-2 IF A 30 cm AXIAL-FLOW PUMP HAVING THE CHARACTERISTICS SHOWN IN FIG. 8-5 IS OPERATED AT A SPEED OF 800 RPM. WHAT HEAD ΔH WILL BE DEVELOPED WHEN THE WATER PUMPING RATE IS 0.127 m3/s? WHAT POWER IS REQUIRED FOR THIS OPERATION? D = 30 cm = 0.30 m. n = 800 rpm / (60 s/m) = 13.33 rps FIRST COMPUTE CQ = Q / (nD3) CQ = 0.127 m3/s / [13.33 rps × 0.303 m3] CQ = 0.353 NOW ENTER FIG. 8-5 WITH CQ = 0.353, AND READ OFF CH = 1.60 AND CP = 0.80 THEN, FROM CH = ΔH / (D2n2 / g) ΔH = CH D2n2 / g ΔH = 1.6 (0.3)2 (13.33)2 / 9.81 ΔH = 2.61 m FROM CP = P / (ρD5n3) THEN: P = CP ρD5n3 P = 0.8 (1.0 KNs2/m4) (0.305 m5) (13.333 s-3) P = 4.6 KN m/s P = 4.6 KW RADIAL AND MIXED-FLOW PUMPS AXIAL FLOW PUMPS ARE BEST SUITED FOR RELATIVELY LOW HEADS AND HIGH RATES OF FLOW. PUMPS USE FOR DEWATERING LOWLANDS, SUCH AS THOSE BEHIND DIKES, ARE ALMOST ALWAYS OF THE AXIAL-FLOW TYPE. FOR LARGER HEADS, RADIAL OR MIXED-FLOW MACHINES ARE MORE EFFICIENT. RADIAL FLOW PUMPS (CENTRIFUGAL PUMPS) LIQUID FROM THE INLET PIPE ENTERS THROUGH THE EYE OF THE IMPELER, THEN TRAVELS OUT WARDS BETWEEN THE VANES OF THE IMPELER TO THE EDGE OF THE IMPELER, WHEN THE FLUID ENTERS THE CASING OF THE PUMP AND IS THEN CONDUCTED TO THE DISCHARGE PIPE. THE CHANGE IN PRESSURE RESULTS LARGELY FROM ROTARY ACTION (PRESSURE INCREASING OUTWARD LIKE THAT OF A ROTATING TANK OF WATER). Ocean Outfall Booster Pump Station, Orange County Sanitation District, Huntington Beach, California. SAME SIMILARITY PARAMETERS APPLY FOR BOTH AXIAL AND RADIAL FLOW PUMPS. THE MAJOR DIFFERENCE IS IN THE PERFORMANCE CHARACTERISTICS OF THE TWO PUMPS. FIG 8-8 SHOWS DIMENSIONAL PERFORMANCE CURVES FOR A TYPICAL RADIAL FLOW PUMP OPERATING AT A CONSTANT SPEED OF ROTATION. 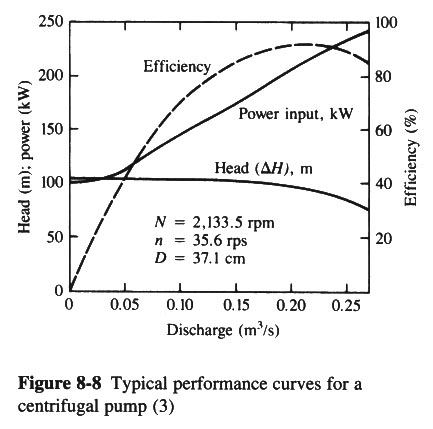FIG 8-9 SHOWS DIMENSIONLESS PERFORMANCE CURVES FOR A TYPICAL RADIAL FLOW PUMP OPERATING AT A CONSTANT SPEED OF ROTATION. 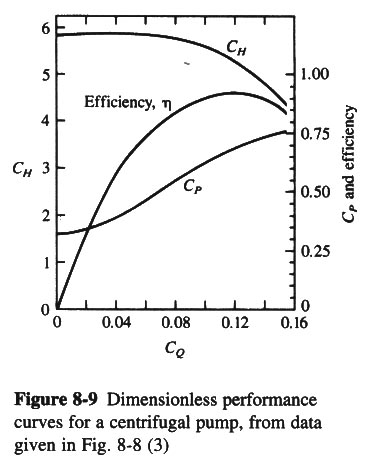NOTE THAT AT SHUTOFF FLOW, THE POWER REQUIRED IS LESS THAN THE POWER FOR FLOW AT MAXIMUM EFFICIENCY. NORMALLY THE MOTOR TO DRIVE THE PUMP WILL BE CHOSEN FOR CONDITIONS OF MAXIMUM PUMP EFFICIENCY. THEN THE FLOW CAN BE THROTTLED BETWEEN THE LIMITS OF SHUTOFF AND NORMAL OPERATING WITHOUT ANY CHANCE OF OVERLOADING THE PUMP MOTOR. THIS IS NOT THE CASE WITH THE AXIAL FLOW PUMP. RADIAL FLOW PUMP OFFERS A DISTINCT ADVANTAGE. RADIAL FLOW PUMPS ARE MANUFACTURED IN SIZES FROM 1 HP OR LESS AND HEADS OF 50 OR 60 FT TO THOUSANDS OF HP AND HEADS OF SEVERAL HUNDRED FEET. EXAMPLE 8-3 THE PUMP HAVING THE CHARACTERISTICS GIVEN IN FIG 8-8, OPERATES AT MAXIMUM EFFICIENCY AT 2133.5 RPM. AT WHAT SPEED N SHOULD THE PUMP BE OPERATED UNDER A HEAD OF 76 M AT MAXIMUM EFFICIENCY? WHAT WILL BE THE DISCHARGE UNDER THESE CONDITIONS? BOTH OPERATING SPEED CONDITIONS (2133.5 AND N) CORRESPOND TO THE POINT OF MAXIMUM EFFICIENCY. THEN: (CH) N = (CH) 2133.5 FROM FIG. 8-8, AT MAXIMUM EFFICIENCY: ΔH = 90 m, AND Q = 0.225 m3/s AT 2133.5 RPM [ΔH / (D2n2 / g)]N = [ΔH / (D2n2 / g)] 2133.5 [ΔH / N2]N = [ΔH / 2133.52] 76 / N2 = 90 / 2133.52 N = 2133.5 (76/90)1/2 = 1960 RPM THEN: (CQ) 1960 = (CQ) 2133.5 CQ = Q / (nD3) [Q / (nD3)] 1960 = [Q / (nD3)] 2133.5 Q1960 / Q2133.5 = 1960 / 2133.5 Q1960 / Q2133.5 = 0.919 Q1960 = 0.919  × Q2133.5 Q1960 = 0.919 (0.225) Q1960 = 0.207 m3/s THE DISCHARGE WHEN THE PUMP IS OPERATED AT MAXIMUM EFFICIENCY AT 1960 RPM IS 0.207 M3/S. EXAMPLE 8-4 THE PUMP SHOWN IN FIG. 8-8 AND 8-9 IS A MODEL OF A PUMP IN THE COLORADO RIVER AQUEDUCT. FOR A PROTOTYPE THAT IS 5.33 LARGER AND OPERATES AT A SPEED OF 400 RPM, WHAT HEAD, DISCHARGE, AND POWER COULD BE EXPECTED AT MAXIMUM EFFICIENCY? FROM FIG. 8-8:   D = 37.1 cm = 0.371 m. FROM FIG 8-9, FOR MAXIMUM EFFICIENCY CONDITIONS:   CQ = 0.115; CH = 5.35; CP = 0.69 n = (400 / 60) = 6.67 rps NEW D = 0.371 m × 5.33 = 1.98 m HEAD COEFFICIENT CH = ΔH / (D2n2 / g) POWER COEFFICIENT CP = P / (ρD5n3) DISCHARGE COEFFICIENT CQ = Q / (nD3) ΔH = CH (D2n2 / g) = 5.35 × 1.982 × 6.672 / 9.81 =  95 m P = CP (ρD5n3) = 0.69 × 1 × 1.985 × 6.673 =  6231 KW Q = CQ (nD3) = 0.115 × 6.67 × 1.983 =  5.95 m3/s PUMPS OPERATING IN A PIPE SYSTEM HEAD AND DISCHARGE ARE INVERSELY RELATED IN A GIVEN PUMP. WHAT HEAD AND DISCHARGE WILL PREVAIL WHEN A GIVEN PUMP IS OPERATED IN A GIVEN PIPE SYSTEM? SOLUTION: SOLVE PIPE SYSTEM EQUATION TOGETHER WITH PUMP EQUATION (PUMP CURVE) THE POINT WHERE THE TWO CURVES INTERSECT WILL YIELD THE OPERATING CONDITION FOR THE SYSTEM. CONSIDER THE FLOW OF WATER OF FIG. 8-19. 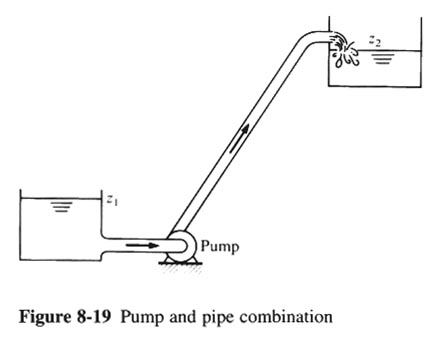p1/γ + V12/(2g) + z1 + hP = p2/γ + V22/(2g) + z2 + ∑ KLV2/(2g) + f (L/D)V2/(2g) p1 = p2 = 0 V1 = V2 = 0 EXIT LOSS KE IS EQUAL TO ONE VELOCITY HEAD. KL = Ke + Σ Kb hp = (z2 - z1) + [V2/(2g)] [1 + ΣKL +  f (L/D)] HENCE, FOR ANY DISCHARGE, A CERTAIN HEAD hp MUST BE SUPPLIED TO MAINTAIN THAT FLOW. THUS, WE CAN CONSTRUCT A HEAD VS DISCHARGE CURVE CALLED THE SYSTEM CURVE (FIG. 8-20). IN ANY PIPE SYSTEM, AS THE DISCHARGE INCREASES, THE HEAD REQUIRED FOR FLOW ALSO INCREASES. WE ALSO PLOT THE HEAD VS DISCHARGE CURVE FOR THE PUMP (FIG. 8-20). 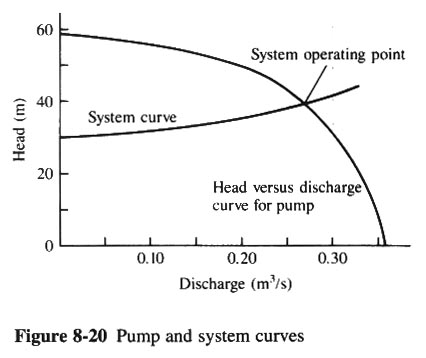FOR ANY PUMP, AS THE DISCHARGE INCREASES, THE HEAD PERFORMED DECREASES. INTERSECTION POINT IS WHERE THE HEAD PRODUCED BY THE PUMP IS JUST THE AMOUNT NEEDED TO OVERCOME THE HEAD LOSS IN THE PIPE AND THE ELEVATION CHANGE. 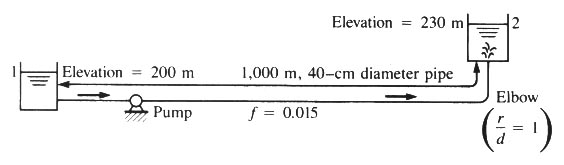EXAMPLE 8-7 WHAT WILL BE THE DISCHARGE IN THE WATER SYSTEM SHOWN BELOW IF THE PUMP HAS THE CHARACTERISTICS SHOWN IN FIG. 8-20? ASSUME SHARP ENTRANCE AND EXIT LOSSES. SOLUTION: hp = (z2 - z1) + [V2/(2g)] [Ke + Kb + KE + f(L/D) ] hp = (230 - 200) + {Q2/(2gA2) }   [0.5 + 0.35 + 1 + 0.015 (1000/0.40)] hp = 30 + {Q2/[2g(π D2/4)2] }   [1.85 + 37.5] hp = 30 + {Q2/[2g(π 0.42/4)2] }   (39.35) hp = 30 + 127 Q2 CALCULATE THE PIPE SYSTEM CURVE Q vs hp. Q (m3/s) hp (m) 0 30 0.1 31.3 0.2 35.1 0.3 41.4 PLOT PIPE SYSTEM CURVE TOGETHER WITH THE HEAD-DISCHARGE CURVE FOR PUMP (FROM FIG. 8-20) TO DETERMINE PIPE/PUMP SYSTEM OPERATING POINT AT Q = 0.27 m3/s. 160224