|
|
CIVE 445 - ENGINEERING HYDROLOGY
CHAPTER 9B: STREAM CHANNEL ROUTING, KINEMATIC WAVES
|
- Three types of unsteady open channel flow waves are common in engineering hydrology:
- kinematic,
- diffusion,
- dynamic
- Kinematic waves are the simplest type of wave.
- Dynamic waves are the most complex.
- Diffusion waves lie somewhere in between kinematic and dynamic waves.
Kinematic wave equation
- The derivation of the kinematic wave equation is based on the principle of mass conservation within a control volume.
- The difference between outflow and inflow within one time interval is balanced by a corresponding change in volume.
- In terms of finite intervals, it is:
|
(Q2 - Q1) Δt + (A2 - A1) Δx = 0
|
- The differential form can be written as:
- The equation of conservation of momentum (Eq. 4-22) contains local inertia,
convective inertia, pressure gradient, friction, gravity, and a momentum source term.
- The kinematic wave uses a statement of steady uniform flow in lieu of conservation of momentum.
- This simplification limits the applicability of kinematic waves.
- The Manning equation of steady uniform flow is:
- The Chezy equation of steady uniform flow is:
- The hydraulic radius R = A/P. Substituting this into the Manning equation leads to:
|
Q = (1/n) (Sf1/2/P2/3) A5/3
|
- Assume that n, Sf and P are constants, for simplicity.
- This is the case of a wide channel with little bed movement.
- This equation can be written as:
in which α and β are parameters of the discharge-area rating.
- Differentiating the discharge-area rating leads to the kinematic wave celerity:
|
dQ/dA = αβAβ-1 = β(Q/A) = βV
|
in which V = mean flow velocity.
- Multiplying the continuity equation with the kinematic wave celerity equation (chain rule), leads to:
|
∂Q/∂t + (dQ/dA) ∂Q/∂x = 0
|
or, alternatively:
- These two equations describe flood wave movement (unsteady flow) under the kinematic wave assumption.
- Kinematic waves travel with celerity βV.
- The kinematic wave equation is a first-order partial differential equation.
- Therefore, it cannot describe diffusion or attenuation.
- Diffusion is a second-order process.
- Since dQ/dA is the celerity, it can be replaced by dx/dt. Therefore:
|
∂Q/∂t + (dx/dt) ∂Q/∂x = 0
|
- This is equal to the total derivative dQ/dt.
|
dQ = (∂Q/∂t) dt + (∂Q/∂x) dx = 0
|
- Since RHS = 0, it follows that Q remains constant in time for waves traveling with celerity dQ/dA.
Discretization of kinematic wave equation
- The kinematic wave equation is nonlinear and of first-order.
- It is nonlinear because the wave celerity varies with discharge.
- The nonlinearity is usually mild, and for some applications, the equation can be considered to be linear.
- The solution can be obtained by analytical or numerical means.
- The simplest kinematic wave solution is a linear numerical solution.
- It is necessary to select a numerical scheme and its properties.
Order of accuracy of numerical schemes
- The order of accuracy of a numerical scheme measures the ability of the numerical scheme to reproduce the terms of the
differential equation being solved.
- In general, the higher the order, the better the reproduction of the differential equation.
- Forward and backward finite-difference schemes have first-order accuracy.
- Central schemes have second-order accuracy.
- First-order schemes create numerical diffusion and dispersion.
- Second-order schemes create only numerical dispersion.
- A third-order scheme of the kinematic wave equation creates neither numerical diffusion or dispersion.
- A third-order scheme reproduces exactly the terms of the differential equation.
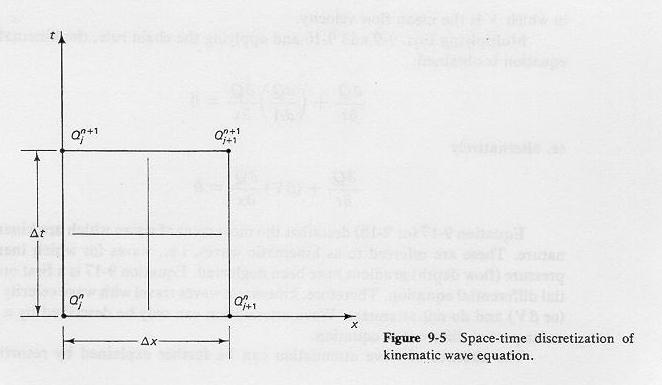
Fig. 9-5
|
- Second-order accurate numerical scheme, central differences in time and space: Example 9-3.
- Second-order accurate numerical scheme: Example 9-3 (continued)
- The Courant number is defined as the ratio of wave celerity βV to the "grid" celerity Δx/Δt:
|
C = βV / (Δx / Δt) = βV (Δt / Δx)
|
- This example illustrates the properties of kinematic waves:
- For C =1, there is no numerical diffusion or dispersion; the solution is a kinematic wave, translated by not diffused.
- For C= 1.5, there is numerical diffusion and dispersion. The diffusion results in slight attenuation; the dispersion causes negative outflows in the tail of the calculated hydrograph.
- The second-order accurate method is impractical because it may lead to negative outflows.
- First-order accurate numerical scheme, backward in time, backward in space: Example 9-4.
- Example 9-4 (continued)
- It is observed that offcentering the derivatives has caused a significant amount of numerical diffusion,
with peak outflow 120.93 m3/sec.
- Different schemes will lead to different answers, depending on the Courant number.
Convex method
- The convex method of channel routing belongs to the family of linear kinematic wave methods.
- Until 1982, it was part of the NRCS (ex SCS) TR-20 hydrologic model.
- The routing equation for the convex method is obtained by discretizing the kinematic wave equation in a linear mode with
forward differences in time and backward differences in space.
- Convex method, forward in time, backward in space: Convex method.
- Convex method (continued)
- Example 9-5 (continued)
- The convex method is relatively simple, but the answer is dependent on the routing parameter C.
- This can be interpreted as a Courant number.
- However, for values of C other than 1, the amount of numerical diffusion is unrelated to the physical diffusion.
- The convex method is a crude approach to stream channel routing.
Kinematic wave celerity
- The kinematic wave celerity is dQ/dA or βV.
- A value β= 5/3 is applicable to a wide channel with Manning friction.
- In 1900, Seddon concluded that the celerity of long disturbances (read kinematic and diffusion waves)
was equal to dQ/dA.
- Since dA= T dy, where T is the channel top width, the Seddon law is expressed in practice as:
- with c = kinematic wave celerity.
- The kinematic wave celerity is a function of the slope of the discharge-stage rating and the channel top width.
- Since both dQ/dy and T vary with stage, c varies with the stage.
- If c = βV is a function of Q, then the kinematic wave equation is nonlinear.
- Nonlinear solutions account for the variation of c with stage and flow level.
- Linear solutions assume a constant value of c.
- Note that there is a striking similarity between linear kinematic wave solutions and the Muskingum method.
- Theoretical β values other than 5/3 can be obtained for other friction formulations and cross-sectional shapes.
- For laminar flow, β = 3.
- For a wide channel with Chezy friction, β = 3/2.
- Calculation of β as a function of frictional type and cross-sectional shape:
Example 9-6
- Example 9-6 (continued)
Kinematic waves with lateral inflow
- Practical application of stream channel routing often require the specification of lateral inflows.
- The lateral inflow could be concentrated (tributary flow), or distributed along the channel (groundwater exfiltration or infiltration).
- A mass balance leads to:
- Multiplying this equation by dQ/dA (or βV) leads to:
|
(∂Q/∂t) + (βV) (∂Q/∂x) = (βV) qL
|
Applicability of kinematic waves
- The kinematic wave is a fundamental streamflow property.
- Flood waves which approximate kinematic waves travel with celerity βV and are subject to negligible attenuation (diffusion).
- In practice, flood waves are kinematic if they are of long duration or travel on a channel of steep slope.
- Usually, slopes greater than 1% are kinematic.
- Criteria for the applicability of kinematic waves to overland flow
(Chapter 4, page 145) and stream channel flow has been developed.
- The stream channel criterion is:
- where tr= time-of-rise of the inflow hydrograph; So = bottom slope,
Vo = average velocity, and do = average flow depth.
- For 95 percent accuracy in one period of translation, a value of N = 85 is recommended.
- Example 9-7
Go to
Chapter 9C.
|
