|
|
CIVE 445 - ENGINEERING HYDROLOGY
CHAPTER 9A: STREAM CHANNEL ROUTING, MUSKINGUM METHOD
|
- Stream channel routing uses mathematical relations to calculate outflow from
a stream channel, once inflow, lateral contributions, and channel characteristics are known.
- Stream channel routing implies open-channel flow conditions.
- Channel reach is a specific length of stream channel possessing certain translation and storage properties.
- The terms stream channel routing and flood routing
are used interchangeably.
- This is because most channel routing applications are in flood hydrology.
- Two general approaches to stream channel routing are recognized:
- Hydrologic, and
- Hydraulic.
- Hydrologic channel routing is based on the storage concept (Chapter 4).
- Hydraulic channel routing is based on the principles of mass and momentum conservation.
- Hydraulic channel routing techniques are of three types:
- Kinematic,
- Diffusion,
- Dynamic.
- The dynamic wave is the most complete model of unsteady flow.
- Kinematic and diffusion waves are useful approximations to the dynamic wave.
- In recent years, a new approach has emerged.
- This approach is similar to hydrologic routing but contains enough physical information
to compare favorably with the hydraulic routing methods.
- This is the basis of the Muskingum-Cunge method.
- A typical model consists of:
- There are three types of problems:
- Prediction: system and input are known; output is sought.
- Calibration: input and output are known; system characterization is sought.
- Inversion: system and output are known; input is sought.
- Prediction is the most typical application.
- The Muskingum method of flood routing was developed by McCarthy in the 1930's in connection
with the design of flood protection schemes in the Muskingum river basin, Ohio.
- It is the most widely used method of hydrologic stream channel routing.
- The Muskingum method is based in the differential equation of storage:
- In an ideal channel, storage is a function of inflow and outflow.
- This should be contrasted with reservoirs, where storage is only a function of outflow.
- In the Muskingum method, storage is a linear function of inflow and outflow:
|
S = K [ X I + (1 - X) O ]
|
- in which K and X are routing parameters.
- K is a time constant, or travel time through the reach.
- X is a weighting factor.
- The Muskingum storage equation is a generalization of the linear reservoir equation.
- For X = 0, it reduces to a linear reservoir.
- The discretization of the differential equation of storage on the x-t plane leads to:
|
(I1 + I2) / 2 - (O1 + O2) / 2 = (S2 - S1) / Δt
|
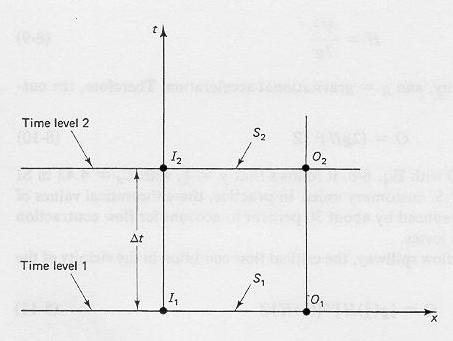
Fig. 8-2
|
- At time level 1:
|
S1 = K [ X I1 + (1 - X) O1 ]
|
- At time level 2:
|
S2 = K [ X I2 + (1 - X) O2 ]
|
- Substituting these equations into the discretized differential equation of storage:
- in which the routing coefficients are defined as follows:
|
C0 = [(Δt/K) - 2X] / [2(1-X) + (Δt/K)]
|
|
C1 = [(Δt/K) + 2X] / [2(1-X) + (Δt/K)]
|
|
C2 = [2(1-X) - (Δt/K)] / [2(1-X) + (Δt/K)]
|
- Since C0 + C1 + C2 = 1, the routing coefficients are interpreted as
weighting coefficients.
- These coefficients are a function of Δt/K and X.
- Given and inflow hydrograph, an initial condition, a time interval Δt and parameters K and X,
the routing proceeds to calculate the outflow hydrograph.
- The parameters K and X are related to flow and channel characteristics.
- K is interpreted as the travel time through the reach (translation).
- K is a function of reach length and flood wave speed.
- X accounts for the storage or diffusion portion of the routing.
- The effect of storage is to reduce the peak flow and spread the hydrograph in time.
- X is a function of the flow and channel characteristics that cause runoff diffusion.
- In the Muskingum method, X is interpreted as a weighting factor restricted in the range 0.0-0.5.
- Values of X greater than 0.5 produce unrealistic hydrograph amplification and should be avoided.
- For K = Δt and X = 0.5, the hydrograph is translated downstream without diffusion (kinematic wave).
- In practice, parameters K and X are determined by calibration using streamflow records (inflow and outflow).
- This is a trial-and-error procedure, which can be readily computerized.
- The procedure lacks predictive capability.
- Values of K and X determined in this way are valid only for the reach and flood event used in the calibration.
- Extrapolation to other reaches or other flood events (within the same reach) is usually unwarranted.
- When sufficient data is available, a calibration can be performed for several flood levels.
- In this way, the variation of K as a function of flood level can be ascertained.
- X is sensitive to time-of-rise of the inflow hydrograph.
-
Example 9-1 and Figure 9-2, showing sketch of the variation of K with stage.
-
Example 9-1 (continuation).
-
Unlike reservoir routing: - stream channel routing exhibits a definite lag between the start of inflow and the start
of outflow
- maximum outflow does not occur at the time that inflow and outflow coincide.
- The calibration problem is shown in
Example 9-2 .
Example 9-2 (continuation 1).
Example 9-2 (continuation 2).
- The parameters K and X tend to vary with flow rate and time-of-rise (nonlinear effect).
- In the Muskingum-Cunge method, the parameters are related to flow and channel characteristics.
- This eliminates the need for trial-and-error calibration.
- Parameter K is related to reach length and flood wave velocity (celerity).
- Parameter X is related to the diffusivity characteristics of the flow and channel.
Go to Chapter 9B.
|