|
|
CIVE 445 - ENGINEERING HYDROLOGY
CHAPTER 9C: STREAM CHANNEL ROUTING, DIFFUSION WAVES
|
- The Muskingum method and a numerical solution of the linear kinematic wave equation show striking similarities.
- Both methods have the same type of routing equation.
- The Muskingum method can calculate hydrograph diffusion.
- The linear kinematic method can calculate hydrograph diffusion only by the introduction of numerical diffusion.
- The latter is dependent on the grid size and type of scheme.
- Kinematic wave theory can be enhanced by allowing a small amount of physical diffusion in its formulation.
- This leads to an improved type of kinematic-with-diffusion wave, for short, a diffusion wave.
- Some diffusion is usually present in natural stream channel situations.
Diffusion wave equation
- The kinematic wave equation was derived using a statement of steady uniform flow in lieu of momentum conservation.
- In the diffusion wave equation, we use a statement of steady nonuniform flow.
- This leads to a slightly modified form of the Manning equation:
|
Q = (1/n) A R2/3 [So - (dy/dx)]1/2
|
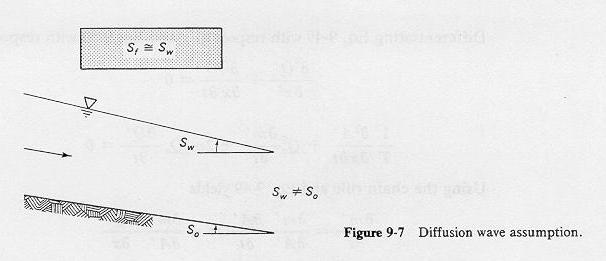
Fig. 9-7
|
- Derivation of the diffusion wave equation:
Diffusion wave equation
- Diffusion wave equation (continued)
- The diffusion wave equation is:
|
∂Q/∂t + (∂Q/∂A) (∂Q/∂x) = [Qo/(2TSo)] (∂2Q/∂2x)
|
- The coefficient of the second-order term (RHS) is the hydraulic or channel diffusivity.
- The hydraulic diffusivity is:
|
νh = Qo /(2TSo)] = qo /(2So)]
|
- The hydraulic diffusivity νh is directly related to unit-width discharge and inversely related to channel slope.
- The diffusion wave equation is a second-order parabolic differential equation.
- It can be solved analytically, leading to Hayami's diffusion-analogy solution for flood waves.
- It can be solved numerically with a Crank-Nicolson scheme.
- Another approach: to match the hydraulic diffusivity with the numerical diffusion coefficient of the Muskingum scheme (kinematic wave
equation).
- This approach is the basis of the Muskingum-Cunge method (Section 9.4).
Applicability of diffusion waves
- Most flood waves have a small amount of physical diffusion.
- Therefore, they are better approximated by the diffusion wave than the kinematic wave.
- Diffusion waves apply to a much wider range of problems than kinematic waves.
- Where the diffusion wave fails, only the dynamic wave can properly describe the translation and diffusion of flood waves.
- The dynamic wave is very strongly diffusive, especially for flows well in the subcritical regime.
- To determine is a wave is a diffusion wave, it should satisfy the following inequality:
- where tr= time-of-rise of the inflow hydrograph; So = bottom slope,
g= gravitational acceleration, and do = average flow depth.
- For 95 percent accuracy in one period of translation, a value of M = 15 is recommended.
- Example 9-8.
Go to
Chapter 9D.
|
