|
| |
|
|
Retratos de amplitud y fase
en el enrutamiento
Muskingum-Cunge
con cálculo en línea
Victor M. Ponce and Bavya Vuppalapati
6 julio 2023
|
|
|
RESUMEN
Se realiza una revisión exhaustiva de los retratos de amplitud y fase del método Muskingum-Cunge de enrutamiento de inundaciones. Las expresiones para las relaciones de convergencia de amplitud y fase R1 y R2, respectivamente, se desarrollan en función de: (a) resolución espacial L/Δx; (b) Número Courant C; y (c) factor de ponderación X.
Se concluye que el modelo de enrutamiento Muskingum-Cunge es una buena representación del prototipo físico, siempre que: (1) la resolución espacial sea suficientemente alta, (2) el número de Courant sea cercano a 1, y (3) el factor de ponderación sea lo suficientemente alto, preferible si está en el rango 0.3 ≤ X ≤ 0.5.
Se desarrollan y prueban dos calculadoras en linea de las relaciones de convergencia, una teórica, basada en parámetros adimensionales, y la otra práctica, basada en variables hidráulicas/hidrológicas reales.
|
1. INTRODUCCIÓN
El concepto de retratos de amplitud y fase en hidráulica computacional se debe a Leendertse (1967). El retrato de amplitud es un gráfico de la relación de amplitud de ondas numérica y analítica, es decir, una relación de convergencia con respecto a la amplitud de onda, en función de variables como la resolución espacial ó la resolución temporal, y el número de Courant. Del mismo modo, el retrato de fase es un gráfico de la relación entre la celeridad de ondas numérica y analítica (una relación de convergencia con respecto a la fase de onda) en función de parámetros numéricos aplicables. Los retratos de amplitud y fase para el método Muskingum-Cunge de enrutamiento de inundaciones fueron desarrollados originalmente por Cunge (1969), y luego ampliados para el problema de convección generalizada (advección) por Ponce et al. (1979a).
El objetivo de los retratos de amplitud y fase es evaluar las propiedades de estabilidad y convergencia de un esquema numérico dado. Esto ayuda a determinar el rango de parámetros discretos (resoluciones espacial y temporal, y su relación correspondiente) para los cuales se puede demostrar que el esquema es estable y convergente. Siguiendo a O'Brien et al. (1950), la estabilidad está relacionada con errores de redondeo, mientras que la convergencia está relacionada con errores de truncamiento es decir, discretización.
En este estudio, revisamos los retratos de amplitud y fase del método Muskingum-Cunge, aclaramos su desarrollo matemático, y explicamos en forma detallada el cálculo, con el objetivo de desarrollar una calculadora en línea.
2. MÉTODO MUSKINGUM-CUNGE
En un artículo seminal, Cunge (1969) elucidó la base de la onda cinemática del método de enrutamiento de inundaciones de Muskingum (Chow, 1959), que condujo al método Muskingum-Cunge (Consejo de Investigación del Medio Ambiente Natural, 1975; Koussis, 1978; Ponce y Yevjevich, 1978). El procedimiento de Cunge permitió el cálculo del factor de ponderación X en términos de parámetros físicos y numéricos, en lugar de confiar únicamente en el caudal, como proponía el método original de Muskingum (McCarthy, 1938). Este concepto revolucionario, basado en la combinación de la difusividad física de Hayami (1951) y la difusividad numérica de Cunge (1969), permite que el hidrograma de avenidas calculado por el método Muskingum-Cunge permanezca independiente de la malla a través de una amplia gama de parámetros (resolución espacial, número de Courant y factor de ponderación). Conviene señalar que esta propiedad fundamental del método Muskingum-Cunge no es compartida por ninguno de los otros métodos de enrutamiento de inundaciones basados en la onda cinemática (Ponce, 1986).
En su artículo original (op. cit.), Cunge expresó los retratos de amplitud y fase en términos de la resolución temporal y un tipo de número de Courant.
Ponce et al. (1979b) amplió el enfoque de Cunge a todo el conjunto de esquemas numéricos que pueden construirse para resolver la ecuación general de convección (advección). Ponce et al. (op. cit.) optaron por presentar sus hallazgos para las relaciones de convergencia de amplitud y fase en términos de resolución espacial (L/Δx) y el número de Courant C, definido éste ultimo como la relación de la celeridad física c (es decir, la celeridad de la onda cinemática) a la celeridad numérica (la relación de malla Δx/Δt).
En este artículo, revisamos los hallazgos de Ponce et al. (op. cit.) y los aplicamos específicamente al método Muskingum-Cunge.
3. DERIVACIÓN DE ECUACIONES
La ecuación de la onda cinemática es la siguiente (Cunge, 1969; Ponce, 2014a):
∂Q ∂Q
____ + c ____ = 0
∂t ∂x
| (1) |
en la cual Q = caudal, c = celeridad de la onda cinemática, y x y t son variables de espacio y tiempo, respectivamente.
La discretización de la Ec. 1 en el plano x-t (Fig. 1), asumiendo linealidad (c = constante) conduce a lo siguiente (Ponce, 2014b):
X (Q j n+1 - Q j n ) + (1 - X) (Q j+1n+1 - Q j+1 n ) (Q j+1 n - Q j n ) + (Q j+1n+1 - Q
j n+1 )
________________________________________________ + c _______________________________________ = 0
Δt 2 Δx
| (2) |
Fig. 1 Discretización espacial y temporal de la ecuación de la onda cinemática
siguiendo el método Muskingum-Cunge.
Simplificando la Ec. 2:
|
X (Q j n+1 - Q j n ) + (1 - X) (Q j+1n+1 - Q j+1 n ) + 0.5 C [ (Q j+1 n - Q j n ) + (Q j+1n+1 - Q
j n+1 ) ] = 0
| (3) |
en la cual C = número de Courant, definido de la siguiente manera:
La solución de la Ec. 3 se postula en la siguiente forma exponencial (O'Brien et al., 1950; Cunge, 1969):
|
Q = Q* e i (σx - βt )
| (5) |
en la cual σ = (2π/L) es el número de onda, L es la longitud de onda y β = (2π/T)
es el período de onda (Ponce y Simons, 1977).
Reemplazando la Ec. 5 en los diversos componentes de la Ec. 3:
|
Q j n = Q* e i [σj Δx - βn Δt ]
| (6) |
|
Q j+1n = Q* e i [σ (j + 1) Δx - βn Δt ]
| (7) |
|
Q j n+1 = Q* e i [σj Δx - β(n + 1) Δt ]
| (8) |
|
Q j+1n+1 = Q* e i [σj Δx - βn Δt ]
| (9) |
Las Ecuaciones 6 a 9 se pueden expresar respectivamente de la siguiente manera:
e i σj Δx
Qj n = Q* ___________
e i βn Δt
| (10) |
e i σj Δx e i σΔx
Qj+1n = Q* _________________
e i βn Δt
| (11) |
e i σj Δx
Qj n+1 = Q* _________________
e i βn Δt e i βΔt
| (12) |
e i σj Δx e i σ Δx
Qj+1n+1 = Q* ___________________
e i βn Δt e i βΔt
| (13) |
El primer término de la Ecuación 3 es:
e iσj Δx e iσj Δx
X (Q j n+1 - Q j n ) = Q* X [ _________________ - ___________ ]
e iβn Δt e iβΔt e iβnΔt
| (14a) |
e iσj Δx - e iσj Δx e iβΔt
X (Q j n+1 - Q j n ) = Q* X [ __________________________ ]
e iβn Δt e iβΔt
| (14b) |
El segundo término de la Ecuación 3 es:
e iσj Δx e iσΔx e iσj Δx e iσΔx
(1-X ) (Q j+1 n+1 - Q j+1 n ) = Q* (1 - X) [ __________________ - _________________ ]
e iβn Δt e iβΔt e iβnΔt
| (15a) |
e iσj Δx e iσΔx - e iβΔt e iσj Δx e iσΔx
(1-X ) (Q j+1 n+1 - Q j+1 n ) = Q* (1 - X) [ ________________________________________ ]
e iβn Δt e iβΔt
| (15b) |
El tercer término de la Ec. 3 es:
|
(C / 2 ) (Q j+1n+1 - Q j n+1 + Q j+1n - Qj n ) =
| |
C Q* e iσj Δx e iσΔx - e iσjΔx + e iβΔt e iσj Δx e iσΔx - e iβΔt e iσj Δx
________ [ _______________________________________________________________ ]
2 e iβn Δt e iβΔt
| (16) |
Sustituyendo las Ecuaciones. 14b, 15b y 16 en la Ec. 3, dividiendo por Q* e iσj Δx, y eliminando el común denominador, se obtiene:
|
2X (1- e iβΔt ) + 2(1- X )(e iσΔx - e iσΔx e iβΔt ) + C (e iσΔx - 1 + e iβΔt e iσΔx - e iβΔt ) = 0
| (17a) |
|
e iβΔt [ -2X - 2(1-X ) e iσΔx + C e iσΔx - C ] + 2X + 2(1-X ) e iσΔx + C e iσΔx - C = 0
| (17b) |
|
e iβΔt [ 2X + 2(1-X )e iσΔx - C e iσΔx + C ] = 2X + 2(1-X ) e iσΔx + C e iσΔx - C
| (17c) |
2[X + (1-X ) e iσΔx] + C [e iσΔx - 1]
e iβΔt = ____________________________________
2[X + (1-X ) e iσΔx] - C [e iσΔx - 1]
| (17d) |
Reordenando la Ec. 17d y tomando el valor recíproco del lado izquierdo:
2[(1-X) e iσΔx + X] - C [e iσΔx - 1]
e -iβΔt = ____________________________________
2[(1-X) e iσΔx + X] + C [e iσΔx - 1]
| (18) |
Una identidad trigonométrica es (Spiegel, 1971):
en la cual p = cos(σΔx) y q = sin(σΔx).
La resolución espacial es L /Δx.
La cantidad σΔx = (2π/L) Δx = 2π/(L/Δx)
es el número de puntos de cuadrícula por longitud de onda. Sustituyendo la Ecuación 19 en la Ec. 18:
2[(1-X)(p + iq) + X] - C [p + iq - 1]
e -iβΔt = _____________________________________
2[(1-X)(p + iq) + X] + C [p + iq - 1]
| (20a) |
{p [(1-X) - C/2] + X + C/2} + iq [(1-X) - C/2]
e -iβΔt = ______________________________________________
{p [(1-X) + C/2] + X - C/2} + iq [(1-X) + C/2]
| (20b) |
Definiendo por motivos de simplicidad:
|
S = R - C = X - (C/2)
| (22) |
Sustituyendo las Ecuaciones 21 y 22 en la Ec. 20b:
[p (1 - R) + R ] + iq (1 - R )
e -iβΔt = ______________________________
[p (1 - S) + S ] + iq (1 - S )
| (23) |
Multiplicando el lado derecho de la Ec. 23 por el conjugado del denominador:
[p (1 - R) + R ] + iq (1 - R ) [p (1 - S) + S ] - iq (1 - S )
e -iβΔt = ______________________________ • ______________________________
[p (1 - S) + S ] + iq (1 - S ) [p (1 - S) + S ] - iq (1 - S )
| (24) |
{[p(1-R) + R ] [p(1-S) + S ] + q 2(1-R) (1-S)} + iq {(1-R) [p(1-S) + S ] - (1-S) [p(1-R) + R ]}
e -iβΔt = ____________________________________________________________________________________________
[ p (1-S )
+ S ] 2 + [ q (1-S )] 2
| (25) |
Ahora examinamos los componentes de la Ecuación 25. Primero considere la parte real [PRN] del numerador del lado derecho de la Ec. 25:
|
[PRN] = [p (1-R) + R ] [p (1-S) + S ] + q 2(1-R ) (1-S )
| (26) |
Operando en la Ec. 26, y después de alguna manipulación algebraica:
|
[PRN] = 1 - (1-p) [R + S - 2RS]
| (27) |
Dado que S = R - C, esto lleva a
R = S + C. Así, en la Ec. 27:
|
[PRN] = 1 - [ 2(1 - p)(1 - S)S ] - [ (1-p)(1 - 2S)C ]
| (28) |
Considerando la parte imaginaria [PIN] del numerador de la Ec. 25:
|
[PIN] = q {(1-R ) [p (1-S ) + S ] - (1-S )[p (1-R ) + R ]}
| (29) |
Operando en la Ec. 29, y después de alguna manipulación algebraica:
Reemplazando R = S + C de la Ecuación 22 resulta en:
Considerando el denominador [DN] de la Ecuación 25:
|
[DN] = [p (1-S ) + S ]2 + [q(1-S )]2
| (32) |
Después de algunas manipulaciones algebraicas:
|
[DN] = 1 - 2 (1 - p)(1 - S) S
| (33) |
Definiendo por motivo de simplicidad:
|
P = 1 - 2 (1 - p)(1 - S) S
| (34) |
Por lo tanto, la Ecuación 25 se puede escribir de la siguiente manera:
P - M - iN
e -iβΔt = ______________
P
| (37a) |
la cual se puede expresar de la siguiente manera:
P - M N
e -iβΔt = _________ - i ______
P P
| (37b) |
En el lado izquierdo de la Ec. 37b, separando β en sus partes real e imaginaria:
|
e -iβΔt = e -i (βR + i βI) Δt = e -i βR Δt e βI Δt
| (38a) |
|
e -iβΔt = e βI Δt e -i βR Δt = a eiφ
| (38b) |
en la cual a = e βI Δt, y eiφ = e i (-βR Δt)
En el lado derecho de la Ec. 38a, tomando el logaritmo natural:
|
ln (e -i βR Δt e βI Δt) = ln e βI Δt - i βR Δt
| (39) |
La Ecuación 37b se puede expresar de la forma z = x + iy, en la cual:
P - M
x = ________
P
| (41) |
La solución de la Ec. 40 es (Spiegel, 1971):
|
ln(a eiφ) = ln (x2 + y2)1/2 + i tan-1(y / x)
| (43) |
Sustituyendo las Ecuaciones. 38b, 41 y 42 en la Ec. 43:
{(P - M)2 + N 2}1/2 N
ln e βI Δt - i βR Δt = ln [ ____________________ ] - i tan-1( _________ )
P P - M
| (44) |
Separando la Ecuación 44 en sus componentes real e imaginario:
[(P - M)2 + N 2]1/2
e βI Δt = ____________________
P
| (45) |
N
tan (βR Δt) = __________
P - M
| (46) |
Dado que la Ecuación 1 no permite el amortiguamiento de onda (eδ = 1, en la cual δ = decremento logarítmico
(Ponce y Simons, 1977), se concluye que la Ec. 45 es una medida del amortiguamiento numérico (signo - ) o amplificación numérica (signo + ) de la solución de la Ec. 3 después de un incremento de tiempo Δt.
4. RELACIONES DE CONVERGENCIA
Siguiendo Ponce et al. (1979c), una relación de convergencia con respecto a la amplitud de onda es:
en la cual:
[(P - M)2 + N 2]1/2
R1 = ____________________
P
| (48) |
La celeridad de la solución numérica es:
Usando las Ecuaciones 46 y 49, una relación de convergencia con respecto a la fase de onda se define como sigue:
cn 1 N
R2 = _____ = ________ tan-1 ( _________ )
c σ c Δt P - M
| (50) |
en la cual cn es la celeridad de onda de la solución numérica, c es la celeridad de onda cinemática (en la Ec. 1), y σ es el número de onda.
De la Ecuación 4: C Δx = c Δ t. Por lo tanto:
1 N
R2 = _________ tan-1 ( ________ )
C σΔx P - M
| (51) |
En resumen, dado sólo: -
Factor de ponderación X,
- Resolución espacial L/Δx, de la cual: σΔx
= (2π /L) Δx = 2 π / (L /Δx),
y
- Número de Courant C,
las Ecuaciones 48 y 51 permiten el cálculo de las relaciones de convergencia de amplitud y fase del método Muskingum-Cunge, respectivamente.
El cálculo de las relaciones de convergencia se realiza utilizando la calculadora
Retrato de convergencia Muskingum-Cunge en línea.
5. RETRATOS DE AMPLITUD Y FASE
El trazado de las relaciones de convergencia R1 and
R2 en función del número de Courant C y la resolución espacial L/Δx
conduce a un conjunto de retratos de amplitud y fase, un par para cada valor del factor de ponderación X.
Las Figuras 2 a 8 muestran los retratos de amplitud y fase del método Muskingum-Cunge (Ec. 3), para números de Courant que varían en el rango 0.1 ≤ C ≤ 4.0, resolución espacial 20 ≤ L/Δx ≤ 100, a intervalos de L/Δx = 20, y factor de ponderación 0.0 ≤ X ≤ 0.6, a intervalos de X = 0.1 (7 × 2 = 14 gráficos).
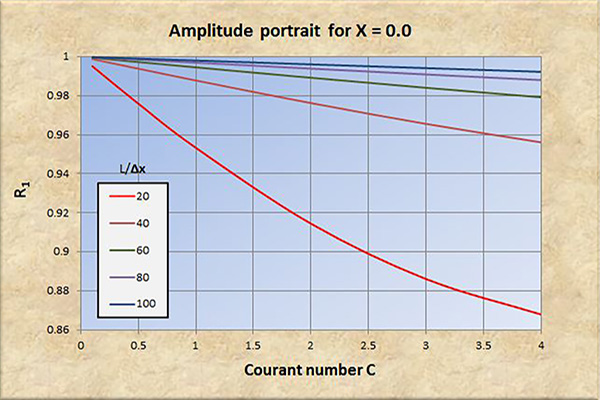
Fig. 2 (a) Retrato de amplitud para X = 0.
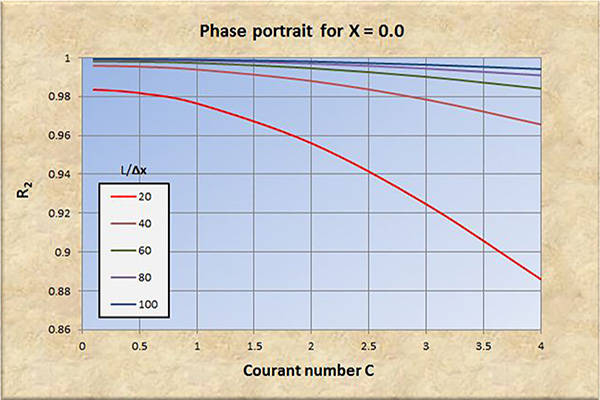
Fig. 2 (b) Retrato de fase para X = 0.
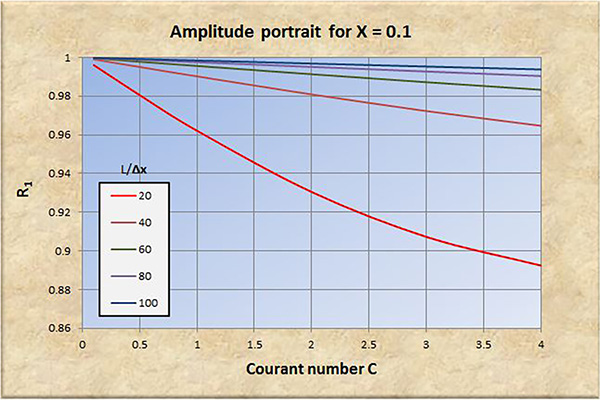
Fig. 3 (a) Retrato de amplitud para X = 0.1.
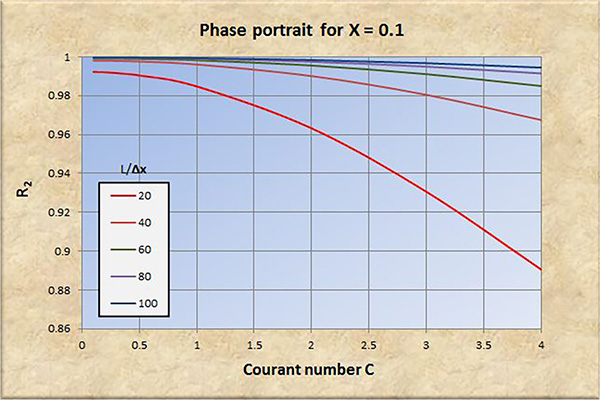
Fig. 3 (b) Retrato de fase para X = 0.1.
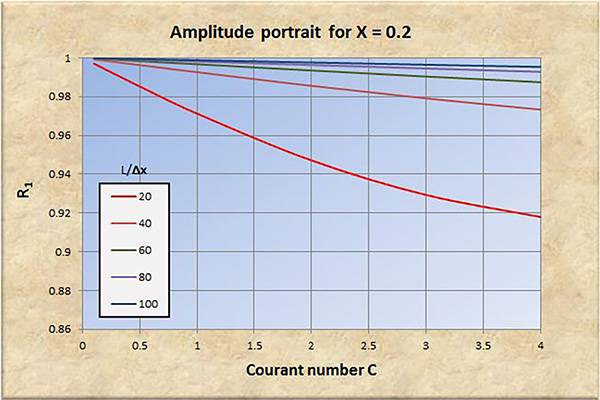
Fig. 4 (a) Retrato de amplitud para X = 0.2.
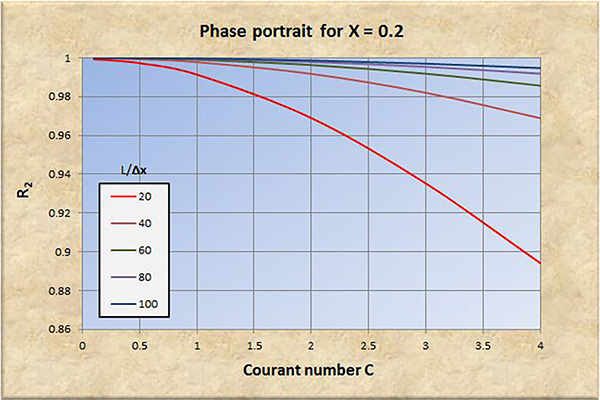
Fig. 4 (b) Retrato de fase para X = 0.2.
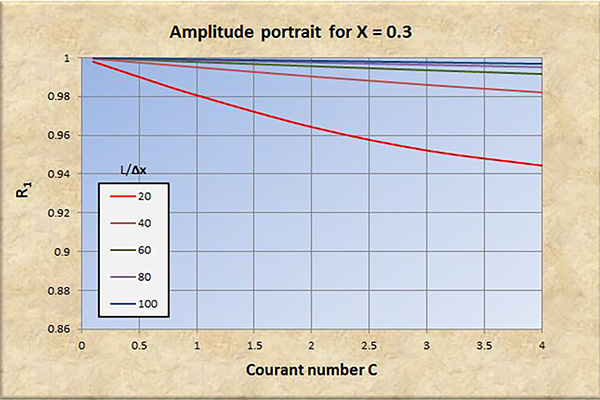
Fig. 5 (a) Retrato de amplitud para X = 0.3.
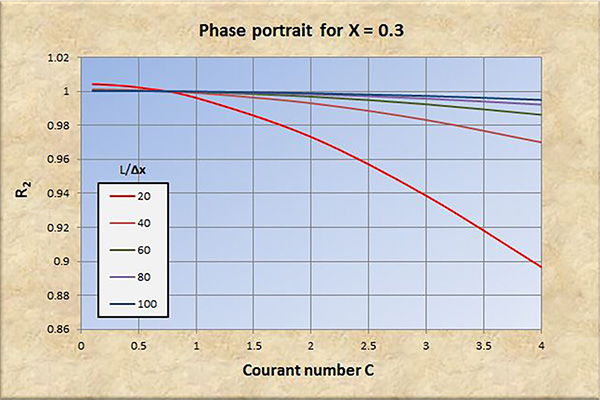
Fig. 5 (b) Retrato de fase para X = 0.3.
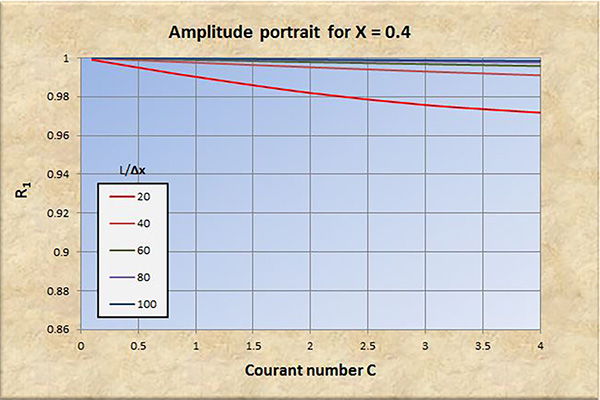
Fig. 6 (a) Retrato de amplitud para X = 0.4.
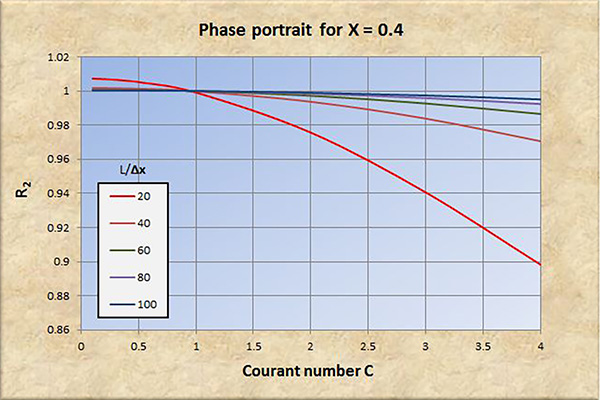
Fig. 6 (b) Retrato de fase para X = 0.4.
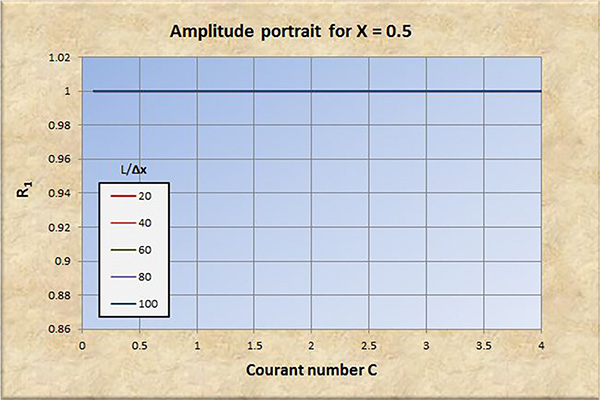
Fig. 7 (a) Retrato de amplitud para X = 0.5.
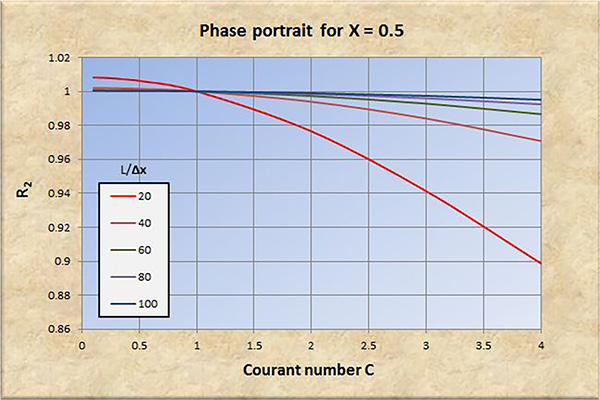
Fig. 7 (b) Retrato de fase para X = 0.5.
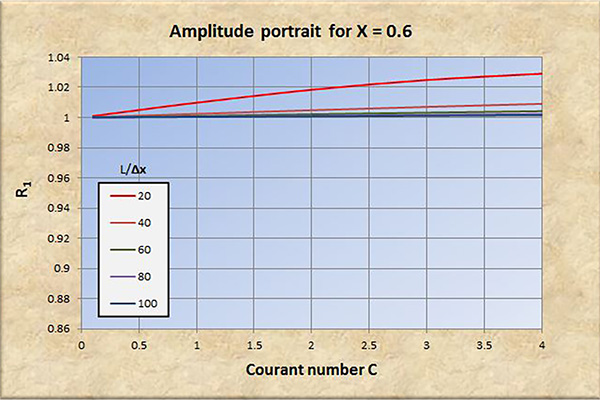
Fig. 8 (a) Retrato de amplitud para X = 0.6.
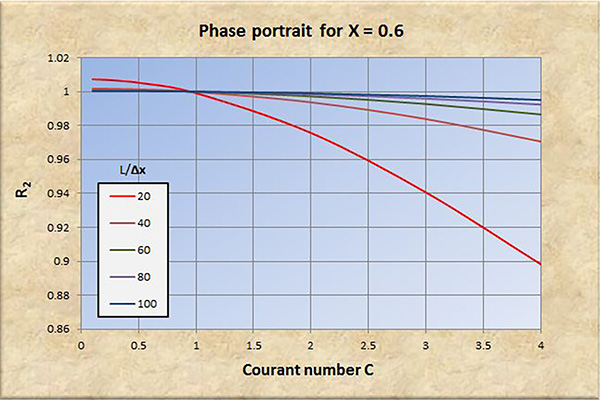
Fig. 8 (b) Retrato de fase para X = 0.6.
6. ANÁLISIS
El examen de las Figs. 2 a 8 conduce a las siguientes conclusiones:
La convergencia perfecta se logra para X = 0.5 y número de Courant C = 1.
La convergencia, tanto en amplitud como en fase, mejora con un aumento en la resolución espacial (L/Δx).
La convergencia, tanto en amplitud como en fase, se degrada con un aumento en el número de Courant C, particularmente para C > 1.
La convergencia en amplitud mejora con un aumento de X en el rango 0 ≤ X ≤ 0.5.
La convergencia en fase mejora ligeramente con un aumento de X en el rango 0 ≤ X ≤ 0.5.
A resoluciones espaciales bajas [consultar las curvas rojas en las Figs. 2 (b) a 8 (b)], la convergencia de fase se degrada significativamente con números de Courant en el rango C < 1, lo que lleva eventualmente a la inestabilidad.
Para X > 0.5, la relación de convergencia de amplitud R1 se vuelve positiva (amplificación), y la convergencia y la estabilidad se degradan a consecuencia de esto.
Concluimos que el modelo Muskingum-Cunge es una buena representación del prototipo físico, siempre que:
La resolución espacial sea suficientemente alta.
El número de Courant esté cerca de 1.
El factor de ponderación sea lo suficientemente alto, en el rango 0.0 ≤ X ≤ 0.5.
Con base en el análisis realizado en este artículo, los valores de los parámetros recomendados para una convergencia adecuada son: (a) resolución espacial L/Δx ≥ 100; (b) número de Courant C ≅ 1; y (c) factor de ponderación 0.3 ≤ X ≤ 0.5.
7. APLICACIONES PRÁCTICAS
En aplicaciones prácticas, la convergencia del método Muskingum-Cunge depende de los valores de los números de Courant y de Reynolds de la malla, los que a su vez dependen de la hidráulica del flujo y del tamaño de la malla (Δx y Δt) (Ponce, 2014c). Se puede calcular un conjunto de relaciones de convergencia de amplitud y fase en términos de variables hidráulicas e hidrológicas.
Con este fin, definimos el tiempo de subida tr de la onda de avenida como el tiempo que tarda ésta en alcanzar el caudal máximo. Suponiendo una perturbación sinusoidal como primera aproximación, la base de tiempo o período de onda T es:
La celeridad de onda c es:
en la cual u = velocidad media del flujo.
En flujo turbulento en canales, el valor de β varía desde β = 5/3 para un canal hidráulicamente ancho, hasta β = 1 para un canal inherentemente estable (Ponce y Porras, 1995;
Ponce, 2014d).
La longitud de onda L de la perturbación es:
El caudal de ancho unitario q es:
en la cual d = profundidad media del flujo. La resolución espacial es L/Δx.
El número de Courant (Ec. 4), repetido aquí con un nuevo número de ecuación, es:
El número de Reynolds de la malla se define de la siguiente manera (Ponce, 2014e):
q
D = ___________
So c Δx
| (57) |
Por definición, el factor de ponderación X de Muskingum-Cunge es:
1
X = ____ (1 - D)
2
| (58) |
Para un caso dado, las Ecs. 52 a 58, junto con las Ecs. 48 y 51, permiten el cálculo de las relaciones prácticas de convergencia del método Muskingum-Cunge, en base a datos reales, es decir, a la hidráulica del flujo.
El cálculo práctico de los coeficientes de convergencia de Muskingum-Cunge se puede realizar utilizando la calculadora
en línea Muskingum-Cunge Convergence Ratios prácticos.
Por ejemplo, suponga los siguientes datos: (1) velocidad media u = 1.75 m/s; (2) profundidad media d = 2.3 m;
(3) pendiente media S = 0.0013; exponente de la curva de gasto β = 1.6, (5) tiempo de subida de la onda de avenida tr = 24 hr;
(6) longitud del tramo Δx = 4,800 m, y (7) intervalo de tiempo Δt = 0.5 hr. La aplicación
práctica de las relaciones de convergencia de Muskingum-Cunge en línea conduce a: R1 = 0.99953; R2 = 0.999915.
En este caso, la resolución espacial es L/Δx = 100.8; el número de Courant es C = 1.05; y el factor de ponderación es X =
0.385. Los tres parámetros se encuentran dentro de los rangos recomendados para una convergencia adecuada.
8. CONCLUSIONES
Se realiza una revisión exhaustiva de los retratos de amplitud y fase del método Muskingum-Cunge. Las expresiones para la relación de convergencia de amplitud R1 y la relación de convergencia de fase R2 se desarrollan en función de: (a) resolución espacial L/Δx; (b) número de Courant C; y (c) factor de ponderación X.
La calculadora
Relaciones de Convergencia Muskingum-Cunge en línea se desarrolla y prueba utilizando un conjunto de datos hipotéticos.
En aplicaciones prácticas, las relaciones de convergencia pueden expresarse alternativamente en términos de variables hidráulicas (velocidad media, profundidad de flujo, pendiente del canal, exponente de la curva de gasto, y tiempo de subida de la onda de avenida). Para este caso, también se desarrolla y prueba una calculadora en línea
Relaciones prácticas de Convergencia Muskingum-Cunge en línea.
BIBLIOGRAFÍA
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York.
Cunge, J. A.. 1969.
On the subject of a flood propagation computation method (Muskingum method). Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.
Hayami, S. 1951. On the propagation of flood waves. Bulletin No. 1, Disaster Prevention Research Institute,
Kyoto University, Kyoto, Japan, December.
Koussis, A. 1978. Theoretical estimation of flood routing parameters. Journal of the Hydraulics Division, ASCE,
Vol. 104, No. HY1, Proc. Paper 13456, January, 109-115.
Leendertse, J. J. 1967. Aspects of a computational model for long-period water wave propagation. Report RM-5294-PR, The Rand Corporation,
Santa Monica, California, May.
McCarthy, G. T. 1938. The unit hydrograph and flood routing. Unpublished manuscript, presented at a conference of the North Atlantic Division,
U.S. Army Corps of Engineers, June 24, 1938.
Natural Environment Research Council. 1975. Flood Studies Report, Vol. III: Flood Routing Studies, London, England.
O'Brien, G. G., M. A. Hyman, and S. Kaplan. 1950. A study of the numerical solution of partial differential equations.
Journal of Mathematics
and Physics, Vol. 29, No. 4, 223-251.
Ponce, V. M., and D. B. Simons. 1977. Shallow wave propagation in open channel flow.
Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, December, 1461-1476.
Ponce, V. M., and V. Yevjevich. 1978.
Muskingum-Cunge method with variable parameters.
Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY12, December, 1663-1667.
Ponce, V. M., Y. H. Chen, and D. B. Simons. 1979. Unconditional stability in convection computations. Journal of the Hydraulics Division, ASCE, Vol. 105, No. HY9, September, 1079-1086.
Ponce, V. M. 1986. Diffusion wave modeling of catchment dynamics.
Journal of Hydraulic Engineering, ASCE, Vol. 112, No. 8, August, 716-727.
Ponce, V. M., and P. J. Porras. 1995. Effect of cross-sectional shape on free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4,
April, 376-380.
Ponce, V. M. 2014. Fundamentals of open-channel hydraulics.
Online text.
Spiegel, M. R. 1971. Advanced mathematics for engineers and scientists. Schaum's Outline Series, McGraw-Hill Inc., New York.
|