1.  INTRODUCCIÓN

El método Muskingum-Cunge de enrutamiento de inundaciones está bien establecido en la literatura de la ingeniería hidrológica (Cunge, 1969; Ponce y Yevjevich, 1978; US Army Corps of Engineers, 1990). Es un método conveniente porque los parámetros de enrutamiento son función de las propiedades del canal y el tamaño de la malla, lo que conduce a resultados que son independientes del tamaño de la malla. El método tiene modos lineales y no lineales. En el modo lineal, los valores promedio de flujo se utilizan para calcular los parámetros de enrutamiento al inicio del cálculo, manteniéndose constantes a lo largo del cálculo en el tiempo. En el modo no lineal, los parámetros de enrutamiento se recalculan para cada célula en función de los valores de flujo locales.

Ambos modos de cálculo tienen sus ventajas y desventajas. El modo lineal conserva la masa, pero requiere una estimación a priori de un flujo de referencia en el cual basar el cálculo de los parámetros de enrutamiento. Además, los caudales enrutados carecen del empinamiento que presentan las ondas de inundación que viajan dentro del canal principal. Por el contrario, el modo no lineal no requiere la especificación de un flujo de referencia y puede simular el empinamiento de la onda. Sin embargo, el modo no lineal produce una pequeña pero perceptible pérdida de masa.

Dadas las diferencias entre los modos de cálculo, parece seguro que ambos modos continuarán utilizándose en el futuro. El modo lineal se utiliza cuando se desee simplicidad, a pesar de la falta de empinamiento de las ondas. El modo no lineal se utilizará cuando se considere importante la simulación del empinamiento/atenuación de las ondas, aunque a costa de una pequeña pérdida de masa. Perumal (1992) ha desarrollado recientemente un método multilineal, el cual representa un compromiso entre métodos lineales y no lineales.

El método Muskingum-Cunge es una alternativa viable al clásico de Muskingum, particularmente para los casos en los que los datos hidrológicos (es decir, datos de caudal) no están disponibles, pero donde los datos hidráulicos (secciones transversales y pendientes de los canales) se pueden obtener fácilmente. En muchos casos, el método Muskingum-Cunge también es una alternativa a los modelos de ondas dinámicas más complejos, los cuales carecen de robustez y requieren gran cantidad de datos. Las características no lineales del método Muskingum-Gunge con parámetros variables lo hacen un buen método para el enrutamiento hidrológico de inundaciones.

Este artículo revisa el método Muskingum-Cunge con parámetros variables de Ponce y Yevjevich (1978). La pequeña pero perceptible pérdida de masa se confirma a lo largo de una amplia gama de descargas pico unitarias, de 200 a 1000 pies cúbicos por segundo por pie (18.58-92.9 m^-2s^-1). Además, se logra una ligera mejora en la conservación de la masa utilizando una forma alternativa de calcular los parámetros variables.

2.  TEORÍA

El método Muskingum-Cunge es una variante del método Muskingum (Chow, 1959) desarrollado por Cunge (1969) y documentado en el Flood Studies Report (Natural Environment Research Council, 1975). Ponce y Yevjevich (1978) expresaron los parámetros de enrutamiento del método en términos de los números de Courant y de Reynolds de la célula, dos parámetros que tienen sentido físico y numérico. Además, desarrollaron un modo no lineal de calcular los parámetros, mejorando así la aplicabilidad del método a los problemas de enrutamiento del mundo real. Se sugirió un método directo de tres puntos y un método iterativo de cuatro puntos como una forma de variar los parámetros en función de los valores de flujo locales. El método ha sido adoptado por la versión más reciente (Versión 4.0) del modelo HEC-1 del Cuerpo de Ingenieros de EE. UU. (1990).

La ecuación de enrutamiento del método Muskingum-Cunge, definido en la configuración típica de la malla de cuatro puntos es la siguiente:

n + 1                 n + 1            n             n            Q j + 1     =   C0Qj       +  C1Qj   +   C2Qj + 1

(1)

en la cual j es un índice espacial, n es un índice temporal, y:

C0 = (-1 + C + D) / (1 + C + D)

(2)

C1 = (1 + C - D) / (1 + C + D)

(3)

C2 = (1 - C + D) / (1 + C + D)

(4)

son los coeficientes de enrutamiento, en las cuales C = número de Courant, definido de la siguiente manera:

C = c (Δt / Δx)

(5)

en la cual c = celeridad de la onda, Δt es el intervalo de tiempo, Δx = intervalo de espacio, y D = número de Reynolds de la célula, definido de la siguiente manera:

D = q /(So c Δx)

(6)

en la cual q = descarga por unidad de ancho y S_o = pendiente de fondo del canal o río.

La celeridad de onda se define de la siguiente manera:

c = β (Q /A) = β (q / d )

(7)

en la cual β = exponente de la curva de gasto, A = área de flujo, y d = profundidad de flujo.

El método Muskingum-Cunge iguala la difusión numérica del modelo discreto con la difusión física del modelo continuo. La ventaja es que los resultados del enrutamiento son independientes de la especificación de la malla, siempre que se minimice la dispersión numérica. La dispersión numérica se puede minimizar manteniendo el número de Courant igual o ligeramente mayor a uno (Cunge, 1969; Ponce y Theurer, 1982; Ferrick et. al., 1983).

3.  EXPERIMENTOS NUMÉRICOS

En este artículo, se eligió el problema clásico de Thomas (1934) para probar el método Muskingum-Cunge en una amplia gama de condiciones de flujo. El problema de Thomas se eligió aquí para permitir la comparación con resultados anteriores (Ponce y Yevjevich, 1978). El problema original consideraba el enrutamiento una una onda de inundación sinusoidal con un período de 96 hr a través de un canal prismático de 500 millas de largo. Se especificó un canal de ancho unitario de flujo base q_b = 50 pies cúbicos por segundo por pie (4.64 m² s^-1) y un flujo máximo de entrada de q_pi = 200 pies cúbicos por segundo por pie (18.58 m² s^-1). La pendiente de fondo se fijó en 1 pie por milla^-1, y la curva de gasto-profundidad esta dada por la siguiente fórmula:

q = 0.688 d 5/3

(8)

Esto equivale a un coeficiente de Manning de n = 0.0297. Puede demostrar que ésta onda de inundación sinusoidal de 96 hr satisface el criterio de aplicabilidad de la onda de difusión (Ponce et. al., 1978).

Aquí consideramos los siguientes métodos:

1. El método de parámetros constantes (MCPC), en el que los parámetros de enrutamiento C y D son los mismos para todas las células. Se basan en una descarga promedio de ancho unitario q_a calculada como sigue:

   qa = (qb + qpi) / 2

   (9)

   
   

   La celeridad media c_a se calcula con la Ec. 7, utilizando la descarga calculada con la Ec. 9.

2. El método de parámetros variables de tres puntos (MCPV3) (Ponce y Yevjevich, 1978), en el cual los parámetros de enrutamiento C y D para cada célula se basan en la descarga promedio por unidad de ancho y la celeridad en los tres puntos conocidos de la malla:

   n         n                n + 1                       qa =  (qj  +   q j + 1   +    q j     ) / 3

   (10)

   
   

   n         n              n + 1                       ca =  ( c j   +  c j + 1  +   c j      ) / 3

   (11)

   
   

3. El método iterativo de cuatro puntos (MCPV4) de parámetros variables (Ponce y Yevjevich, 1978), en el que los parámetros de enrutamiento C y D para cada célula se basan en la descarga promedio por unidad de ancho y la celeridad en los cuatro puntos de la malla:

   n         n               n + 1        n + 1                qa =  (q j   +  q j + 1   +   q j      +   q j + 1    ) / 4

   (12)

   
   

   n         n               n + 1        n + 1                ca =  (c j   +  c j + 1   +   c j      +   c j + 1    ) / 4

   (13)

   
   

   Para mejorar la convergencia del procedimiento iterativo, la descarga q_{j + 1}^{n + 1} se utiliza como primera estimación de la iteración. La celeridad c_{j + 1}^{n + 1} se calcula con la Ec. 7, basado en q_{j + 1}^{n + 1}. La iteración converge a una tolerancia especificada después de algunas iteraciones.

4. Un método modificado de parámetros variables de tres puntos (MCPVM3), en el que los parámetros de enrutamiento C y D para cada célula se basan en la descarga promedio por unidad de ancho en los tres puntos conocidos de la malla:

   n          n               n + 1                       qa =  (q j   +   q j   +  1  +  q j      ) / 3

   (14)

   
   

   A diferencia del MCVP3, la celeridad media c _a se calcula con la Ec. 7, basada en la descarga calculada con la Ec. 14.

5. Un método iterativo modificado de parámetros variables de cuatro puntos (MCPVM4), en el cual los parámetros de enrutamiento C y D para cada célula se basan en la descarga promedio por unidad de ancho en los cuatro puntos de la malla:

   n        n                 n + 1      n + 1                qa =  ( q j   +  q j + 1   +    q j    +   q j + 1    ) / 4

   (15)

   
   

   A diferencia del MCVP4, la celeridad media c _a se calcula con la Ec. 7, basada en la descarga q_a calculada con la Ec. 15. Para mejorar la convergencia del procedimiento iterativo, la descarga q_{j + 1}^{n + 1} obtenida con el método de tres puntos (MCPVM3) se utiliza como primera estimación de la iteración. La iteración converge a una tolerancia especificada después de algunas iteraciones.

Se eligen dos niveles de resolución espacial y temporal:

1. Nivel de resolución I, La especificación de malla utilizada por Thomas (1934): Δx = 25 millas (40.22 km), y Δt = 6 hr; y

2. Nivel de resolución II, una especificación de malla más fina utilizada en este artículo: Δx = 12.5 millas (20.11 km), y Δt = 3 hr.

Se utilizaron tres relaciones de flujo pico de entrada y flujo base q_pi /q_b:

1. q_pi /q_b = 4, usada por Thomas (1934), Dooge (1973), y Ponce y Yevjevich (1978);

2. q_pi /q_b = 10; y

3. q_pi /q_b = 20.

Estas relaciones del flujo de entrada pico y el flujo base abarcan una amplia gama de valores usados en la práctica. Con q_pi = 50 pies cúbicos por segundo por pie (4.64 m²s^-1), el rango de flujo de entrada pico probado fue de 200 - 1000 pies cúbicos por segundo por pie (18.58 - 92.9 m²s^-1).

---

4.  RESULTADOS

Las propiedades de conservación de la masa se evaluaron integrando hidrogramas de entrada y salida para el tramo de 500 millas. La Tabla 1 muestra el flujo pico de salida q_ps, la relación entre el flujo pico de salida y el flujo pico de entrada q_ps / q_pe, en el tiempo pico t_p, y la conservación de la masa M para:

1. Dos niveles de resolución: I y II;

2. Tres relaciones de flujo pico de entrada y flujo base q_pe / q_b: 4, 10 y 20; y

3. Cinco métodos: (a) MCPC; (b) MCPV3; (c) MCPV4; (d) MCPVM3; y (e) MCPVM4.

TABLA 1.  Resumen de los resultados de enrutamiento.
Nivel de resolución (1)	qpe /qb (2)	Método (3)	qps (pie3/s/ pie) (4)	qps /qpe (5)	tp (h) (6)	M (%) (7)
I	4	MCPC	176.231	0.881	126	100.000
		MCPV3	175.097	0.875	120	99.213
		MCPV4	175.860	0.879	120	99.464
		MCPVM3	175.437	0.877	120	99.334
		MCPVM4	176.084	0.880	120	99.559
I	10	MCPC	437.448	0.875	108	100.000
		MCPV3	435.592	0.871	102	97.180
		MCPV4	436.968	0.874	102	98.309
		MCPVM3	435.784	0.872	102	97.904
		MCPVM4	436.939	0.874	102	98.875
I	20	MCPC	876.675	0.877	96	100.000
		MCPV3	876.628	0.877	90	95.370
		MCPV4	878.236	0.878	90	97.444
		MCPVM3	876.160	0.876	90	96.700
		MCPVM4	877.786	0.878	90	98.441
II	4	MCPC	176.561	0.883	129	100.000
		MC3PV	174.146	0.871	123	99.330
		MCPV4	174.370	0.872	123	99.468
		MCPVM3	174.189	0.871	123	99.368
		MCPVM4	174.430	0.872	120	99.498
II	10	MCPC	438.666	0.877	105	100.000
		MCPV3	428.704	0.875	102	97.582
		MCPV4	429.937	0.860	99	98.224
		MCPVM3	429.094	0.858	102	97.847
		MCPVM4	430.580	0.861	99	98.429
II	20	MCPC	884.788	0.885	93	100.000
		MCPV3	866.356	0.866	87	95.943
		MCPV4	870.975	0.871	87	97.163
		MCPVM3	868.557	0.869	87	96.477
		MCPVM4	872.360	0.872	87	97.574
Nota:  Los flujos pico de salida que se muestran en la columna 4 son los correspondientes a las ubicaciones de la malla y no son necesariamente los flujos pico de salida reales, que pueden estar en el intermedio.

La Tabla 1 lleva a las siguientes conclusiones:

1. Los cinco métodos dan aproximadamente el mismo flujo pico de salida q_ps y el tiempo hasta el pico t_p.

2. La relación de flujo pico de salida a flujo pico de entrada (q_ps /q_pe) es aproximadamente la misma para las tres relaciones de flujo pico de entrada a flujo base. Esto sugiere que la difusión de ondas es independiente de la relación q_pe /q_b.

3. El método de parámetros constantes (MCPC) conserva exactamente la masa. Por el contrario, los métodos de parámetros variables están sujetos a una pequeña pero perceptible pérdida de masa. La pérdida de masa es acumulativa y se puede evaluar cuantitativamente mediante el enrutamiento a través de un tramo muy largo. En este caso, el enrutamiento de un hidrograma sinusoidal a través de un tramo de 500 millas produjo pérdidas de masa que van desde menos del 2.5% para MCPVM4 a menos del 5% para MCPV3.

4. La pérdida de masa es mayor para los métodos de tres puntos (MCPV3 y MCPVM3) que para los métodos de cuatro puntos (MCPV4 y MCPVM4).

5. La pérdida de masa es mayor para los métodos convencionales (MCPV3 y MCPV4) que para los métodos modificados (MCPVM3 y MCPVM4).

6. La pérdida de masa aumenta con la relación q_pe /q_b, y no parece estar fuertemente relacionada con el nivel de resolución.

Cabe señalar que los porcentajes de conservación de masa mostrados en la Columna 7 son valores acumulativos para el tramo de 500 millas del problema de Thomas. Una aplicación típica de enrutamiento de inundaciones normalmente no consideraría un tramo tan largo sin la intervención de flujos laterales que tenderían a enmascarar la precisión del cálculo. Por lo tanto, los porcentajes mostrados deben interpretarse como un escenario extremo.

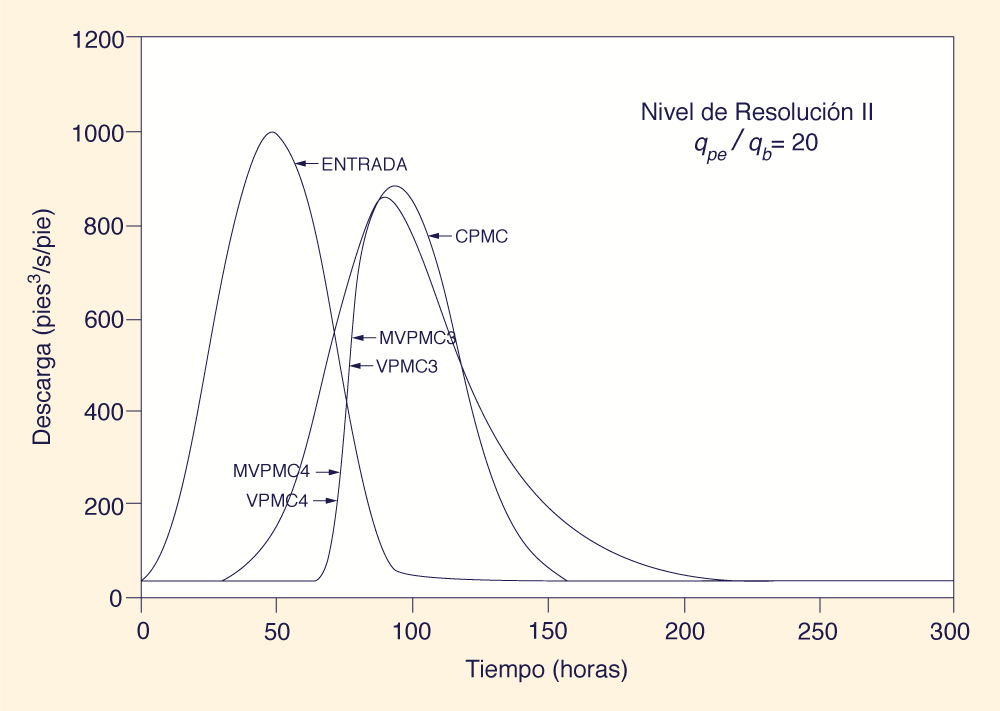
La Figura 1 muestra un conjunto de hidrogramas de inundación para el nivel de resolución II y la relación de flujo pico de entrada al flujo base q_pi /q_b = 20. Se ve que el método de parámetros constantes (MCPC) carece de la tendencia no lineal al empinamiento de la rama ascendente. (Es necesario señalar que los flujos desbordados tienen la tendencia opuesta, es decir, a la atenuación de la rama ascendente). Por otro lado, los cuatro métodos de parámetros variables muestran un empinamiento de la rama ascendente, junto con una atenuación correspondiente de la rama descendente.

Fig. 1.  Hidrogramas de flujo de salida para el nivel de resolución I y la relación de flujo de entrada pico a flujo base qpi /qb = 20.

---

5.  CONCLUSIONES

Los métodos modificados de parámetros variables MCPVM3 y MCPVM4 presentados en este artículo dan como resultado una mejora definitiva en la conservación de la masa, en comparación con los métodos convencionales MCPV3 y MCPV4 (Ponce y Yevjevich, 1978). La mejora puede ser más marcada cuando se utiliza una amplia gama de descargas reales. De otra manera, la pequeña pérdida de masa no parece ser importante. Es el costo del modelado de las características no lineales de una onda de inundación en el marco del método Muskingum-Cunge.

---

BIBLIOGRAFÍA

Chow, V. T. 1959. Open-Channel Hydraulics. McGraw-Hill, New York.

Cunge, J. A. 1969. On the subject of a flood propagation computation method (Muskingum method). J. Hydraul. Res., 7(2) 205-230.

Dooge, J. C. I. 1973. Linear theory of hydrologic systems. U.S. Dep. Agric. Tech. Bull., 1468, 327 pp.

Ferrick, M. G., J. Bilmes, y S. E. Long. 1983. Modeling rapidly varied flow in tailwaters. Water Resour. Res., 20(2): 271-289.

Natural Environment Research Council. 1975. Flood Studies Report, Vol. III. Natural Environment Research Council, London.

Perumal, M. 1992. Multilinear Muskingum flood routing method. J. Hydrol., 133: 259-272.

Ponce, V. M. y F. D. Theurer. 1982. Accuracy criteria in diffusion routing. J. Hydraul. Div., ASCE., 108 (HY6): 747-757.

Ponce, V. M. y V. Yevjevich. 1978. Muskingum-Cunge method with variable parameters. J. Hydraul. Div. ASCE, 104(HY12): 1663-1667.

Ponce, V. M., R. M. Li, y D. B. Simons. 1978. Applicability of knematic and diffusion models. J. Hydraul. Div. ASCE, 104(HY3): 353-360.

Thomas, H. A. 1934. The hydraulics of flood movement in rivers. Eng. Bull., Carnegie Inst. of Technology, Pittsburgh, PA.

US Army Corps of Engineers. 1990. HEC-1, flood hydrograph package: User's manual, version 4, US Army Corps of Engineers, Hydrologic Engineering Center, Davis, CA.

---