|
"Verificación analítica del enrutamiento Muskingum-Cunge".
El método Muskingum-Cunge se ha aplicado con éxito durante muchos años en el enrutamiento, modelado y predicción de inundaciones (Consejo de Investigación del Medio Ambiente Natural 1975; Ponce y Yevjevich, 1978). Cunge (1969) dedujo teóricamente los parámetros de enrutamiento de Muskingum basándose en el error de aproximación obtenido por una expansión de la función de malla en una serie de Taylor. Aunque se ha demostrado que los parámetros así derivados funcionan razonablemente bien en una variedad de aplicaciones prácticas (Centro de Ingeniería Hidrológica, Cuerpo de Ingenieros del Ejército de los EE.UU. ,1990), su vínculo con las expresiones analíticas para la celeridad de las ondas (Seddon, 1900) y la difusividad hidráulica (Hayami, 1951) aún no se ha demostrado.
Este artículo prueba la veracidad del modelo Muskingum-Cunge comparando la celeridad y la atenuación del pico de la onda de avenida, obtenidas analíticamente, con aquéllas obtenidas utilizando una aplicación numérica. La notable concordancia entre los resultados analíticos y numéricos es una indicación de la efectividad del modelo.
El modelo Muskingum-Cunge de enrutamiento de inundaciones (Cunge, 1969; Natural Environment Research Council, 1975) representa una mejora del modelo clásico de Muskingum (Chow, 1959), en el que los parámetros de enrutamiento se basan en datos hidráulicos fácilmente medibles, como la curva de gasto, la pendiente de fondo, el ancho del canal y la longitud del tramo, en lugar de basarse en datos históricos de caudales. Esto permite un extenso enrutamiento en flujos no aforados con una expectativa razonable de precisión, que de otro modo sólo sería posible si los flujos hubieran sido aforados. Dado que no es práctico medir más de unas pocas corrientes, un método que sea preciso y que no dependa de la medición de corrientes es muy prometedor.
Ponce y Yevjevich (1978) mejoraron el modelo de Muskingum-Cunge al expresar los parámetros de enrutamiento como los números adimensionales de Courant y de Reynolds de la célula, en la cual el primero es la relación entre las celeridades física y numérica (Seddon, 1900; O'Brien et al., 1950) y el segundo es la relación de difusividades física y numérica (Hayami, 1951; Cunge, 1969):
en la cual C = número de Courant, D = número de Reynolds de la célula, c = celeridad de la onda de avenida, Δx = intervalo de espacio, Δt = intervalo de tiempo, qo = caudal unitario, y Con los parámetros de enrutamiento de Muskingum definidos de esta manera, los coeficientes de enrutamiento son los siguientes (Ponce y Yevejevich, 1978):
y la ecuación de enrutamiento es la siguiente:
en la cual j = índice espacial y n = índice temporal. La formulación de Cunge (Cunge, 1969) se basa en la teoría de la onda difusiva, cuya aplicabilidad fue confirmada por Ponce et al. (1978). El trabajo analítico pionero sobre la onda de difusión se debe a Hayami (1951), quien razonó que la mezcla longitudinal a gran escala causada por las irregularidades del flujo podría modelarse efectivamente como un proceso de difusión. Ponce y Simons (1977) utilizaron la teoría de la estabilidad lineal para derivar funciones de celeridad y atenuación para perturbaciones sinusoidales del flujo uniforme. En este artículo usamos los hallazgos de Ponce y Simons (1977) para calcular el caudal máximo y el tiempo de traslación analíticos para una serie de hidrogramas sinusoidales, y comparar estos resultados con los obtenidos usando el modelo Muskingum-Cunge (Ecs. 1-6) .
La celeridad de la onda de difusión analítica puede aproximarse como la velocidad o celeridad de Seddon (Ponce y Simons, 1977):
en la cual c = celeridad de la onda de avenida, u = velocidad media, y β = exponente en la curva de gasto:
o, alternativamente, para un canal de ancho unitario:
en la cual Q = descarga, A = área de flujo, q = caudal unitario, y d = profundidad de flujo. La atenuación de la onda sigue una función de decaimiento exponencial de la siguiente forma:
en el cual qpo = caudal pico de salida, qpi = caudal pico de entrada, qo = flujo de equilibrio, El factor de propagación de amplitud es el siguiente (Ponce y Simons, 1977):
en el cual σ* = número de onda adimensional, definido de la siguiente manera:
en el cual L = longitud de onda sinusoidal, y Lo =
longitud del canal de referencia, definida como Desde que L = cT, en la cual T = periodo de onda, tomado como la base de tiempo Tb de un hidrograma sinusoidal, y t* = t (uo /Lo), resulta que:
en la cual ν = qo / (2So) es la difusividad hidráulica (Hayami, 1951).
Este artículo utiliza una extensión del problema clásico de enrutamiento de avenidas de Thomas (1934) para probar la concordancia entre el flujo de salida máximo derivado analítica y numéricamente, y el tiempo de traslación de la onda. El problema de Thomas enruta un hidrograma de inundación sinusoidal de base de tiempo (es decir, período de onda) Tb = 96 h, flujo de entrada máximo qpi = 200 pies cúbicos por segundo, por pie, y caudal base qb = 50 pies cúbicos por segundo, por pie, a través de un canal de longitud Lr = 200 millas, pendiente So = 1 pie/mi y curva de gasto:
a partir del cual se calcula el coeficiente de Manning n = 0.0297.
Se desarrolló una serie de casos de prueba basados en el problema de Thomas, utilizando:
Para Tb = 48 h, el espacio y los intervalos de tiempo elegidos son: Δx = 6.25 mi, y Δt = 1.5 h, respectivamente; para Tb = 96 h, los intervalos son: Δx = 12.5 mi, y Δt = 3 horas. Los períodos de onda elegidos (48 y 96 h) satisfacen los criterios de aplicabilidad de ondas difusivas (Ponce et al., 1978):
en la cual g = aceleración gravitacional. En efecto, para el caso menos favorable (Tb = 48 hr, y
lo cual garantiza que las ondas enrutadas permanezcan dentro del ámbito de las ondas difusivas.
La Tabla 1 resume la comparación del flujo de salida máximo analítico y numérico qpo, y el tiempo de traslación Tt para una serie seleccionada de hidrogramas sinusoidales. El objetivo es comparar los resultados analíticos de las columnas etiquetadas (1) con los resultados numéricos de las columnas etiquetadas (2).
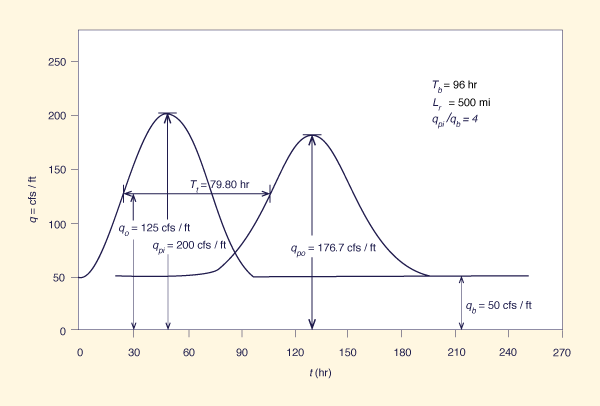
La Figura 1 muestra los hidrogramas de entrada y salida para un caso típico (Tb = 96 hr,
Sobre la base del análisis presentado, se concluye que el enrutamiento Muskingum-Cunge simula con precisión la propagación de ondas de inundación. En doce (12) pruebas que abarcan una amplia gama de condiciones prácticas, la relación de flujos de salida máximos numéricos a analíticos varió dentro del rango 0.991-1.003, y la relación de tiempos de traslación numéricos a analíticos varió dentro del rango 0.987-1.021. La aproximada coincidencia es realmente sorprendente, aún considerando que se utilizó un flujo de referencia constante en el cálculo de los valores analíticos. Estos hallazgos demuestran la utilidad del método Muskingum-Cunge de enrutamiento de inundaciones para su uso en aplicaciones prácticas. BIBLIOGRAFÍA
Chow, V. T., 1950. Open-channel Hydraulics. McGraw-Hill, New York.
Cunge, J. A., 1969. On the subject of a flood propagation computation method (Muskingum method). J. Hydraul. Res., 7(2): 205-230.
Hayami, S., 1951.On the Propagation of flood waves. Disaster Prey. Res. Inst, Kyoto Univ. Bull., 1: 1-16.
Hydrologic Engineering Center, US Army Corps of Engineers, HEC-1, Flood Hydrograph Package. User's Manual. Version 4.0, September, Davis, CA.
Natural Environment Research Council. 1975. Flood Studies Report, Vol. 5: Flood Routing Studies. NERC, London.
O'Brien, G. G., Hyman, M. A. y Kaplan, S., 1950. A study of the numerical solution of partial differential equations. J. Math. Phys., 29(4): 231-251.
Ponce, V. M., 1989. Engineering Hydrology, Principles and Practices. Prentice-Hall, Englewood Cliffs, NJ.
Ponce, V. M. y Simons, D. B, 1977. Shallow wave propagation in open channel flow. J. Hydraul. Div. ASCE. 103(.12): 1461-1476.
Ponce, V. M. y Yevjevich, V., 1978. Muskingum -Cunge method with variable parameter. J. Hydraul. Div. ASCE, 104(HY312): 1663-360.
Ponce, V. M., Li, R. M. y Simons, D., 1978. Applicability of kinematic and diffusion models. J. Hidraul. Div. ASCE, 104(HY3)353-360.
Seddon, J. 1900. River hydraulics. Trans. Am. Soc. Civ. Eng., 431, 179-229.
Thomas, H. A., 1934. The hydraulics of flood movement in rivers. Engineering Bulletin. Carnegie Institute of Technology. Pittsburgh, PA.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 221130 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |