1. INTRODUCTION Roll waves can occur in an unstable free-surface flow regime, i.e., when the Vedernikov number exceeds 1. The flow condition can be either laminar or turbulent. In the laminar regime, an example of roll waves is the pulsating flow often observed in steep urban catchments following intense rainfall. In the turbulent flow regime, roll waves may require a specific type of boundary condition for their inception. The Vedernikov number V > 1 (Vedernikov 1945, 1946) is the necessary condition for roll-wave formation. The existence of this criterion was confirmed by Craya (1952) and lwasa (1954). Using the theory of linear stability, Ponce and Simons (1977) confirmed the Vedernikov criterion for turbulent Chezy friction in hydraulically wide channels. In addition, Ponce and Simons identified the scale of the disturbances under which roll waves are most likely to develop. Brock (1967) experimentally studied roll-wave propagation using a laboratory flume. Brock measured crest depths and wave periods under a wide range of flow conditions for turbulent Chezy friction in hydraulically wide channels. The objective of this note is to use Brock's (1967) laboratory data to test the validity of Ponce and Simons' (1977) theory. Experimental wavenumbers, calculated from wave periods measured by Brock, are compared with wavenumbers predicted by the theory. An approximate match of wavenumbers confirms the validity of the theory. In a practical setting, this knowledge can be used to promote or inhibit the development of roll waves. 2. VEDERNIKOV NUMBER The Vedernikov number is defined as (Chow 1959)
in which x = exponent of hydraulic radius R in the mean velocity functional relation
in which b = exponent of Reynolds number R in the frictional power law f = α(R)-b, in which f = Darcy-Weisbach friction factor. Parameter b varies in the range 0-1, with b = 0 for turbulent Chezy friction; and b = 1 applicable to laminar flow. The shape factor γ is defined as:
in which P = wetted perimeter; and A = cross-sectional flow area. The shape factor γ varies in the range 0-1, with γ = 0 applicable to a channel of constant hydraulic radius R, an inherently stable channel (Liggett 1975; Ponce 1991), and γ = 1 for the case of a hypothetical channel of constant wetted perimeter P, a hydraulically wide channel. 3. THEORY OF ROLL WAVE FORMATION The linear stability analysis of Ponce and Simons (1971) expresses the propagation characteristics of shallow water waves in terms of: (1) the Froude number F of the steady uniform flow; and (2) a dimensionless wavenumber characterizing the unsteady component of the motion. The Froude number is defined as F = u0 / (gd0)1/2; in which u0 = steady uniform mean flow velocity; d0 = steady uniform flow depth; and g = gravitational acceleration. The dimensionless wavenumber is defined as σ = (2π/L)L0; in which L = wavelength of the disturbance; and L0 = reference channel length, defined as the channel length in which the steady uniform flow drops a head equal to its depth.
The propagation characteristics of shallow water waves are: (1) the dimensionless relative wave celerity cr; and (2) the logarithmic decrement δ. The dimensionless relative wave celerity The theoretical expressions for dimensionless wave celerity and logarithmic decrement (Ponce and Simons 1977) are included here for completeness. The dimensionless relative wave celerity is:
in which
and
The logarithmic decrement of the downstream-propagating shallow wave is:
4. RESULTS
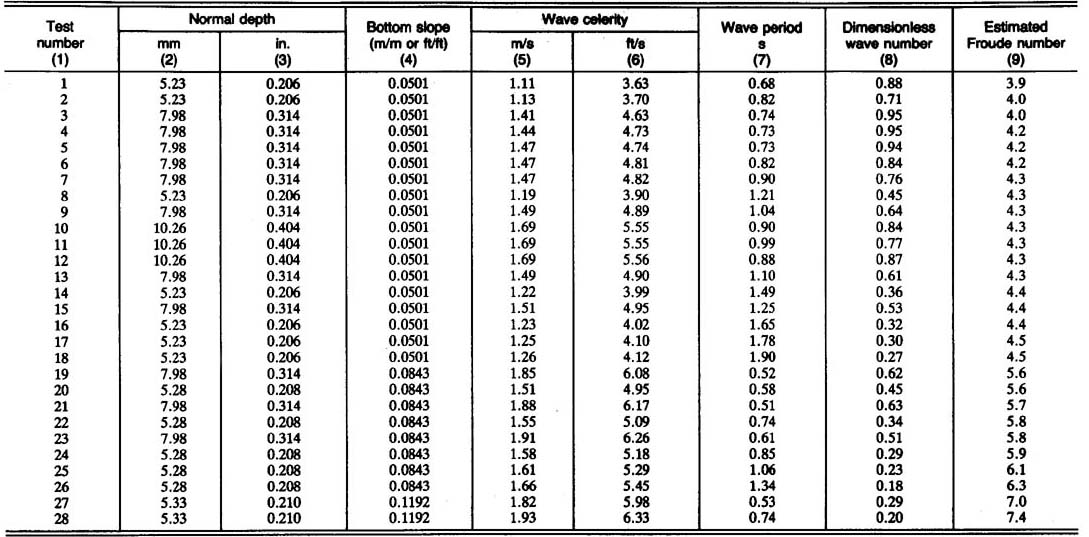
The Brock (1967) data were assembled as shown in Table 1, which
shows the following:
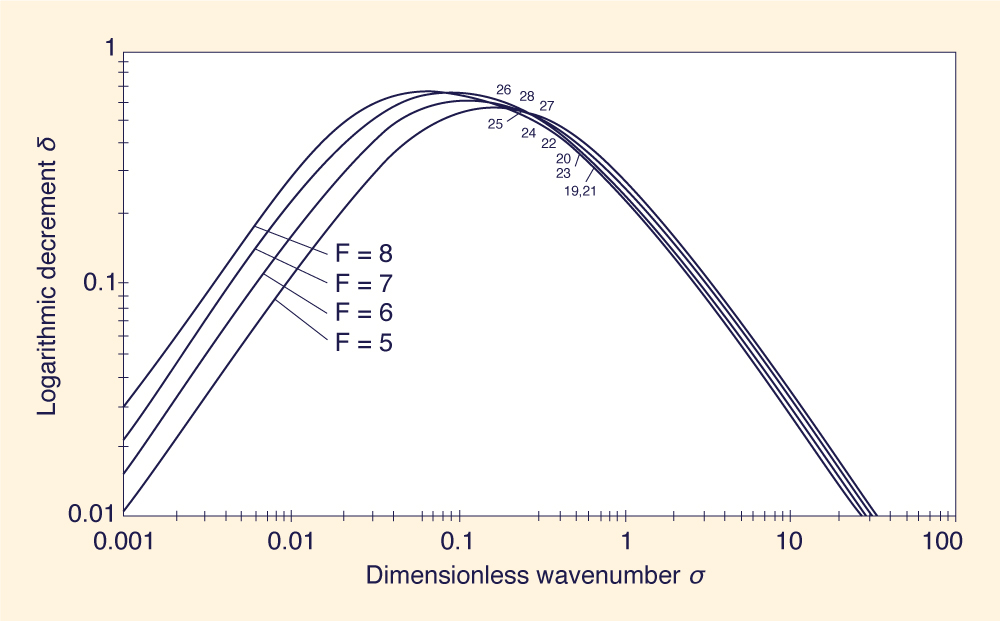
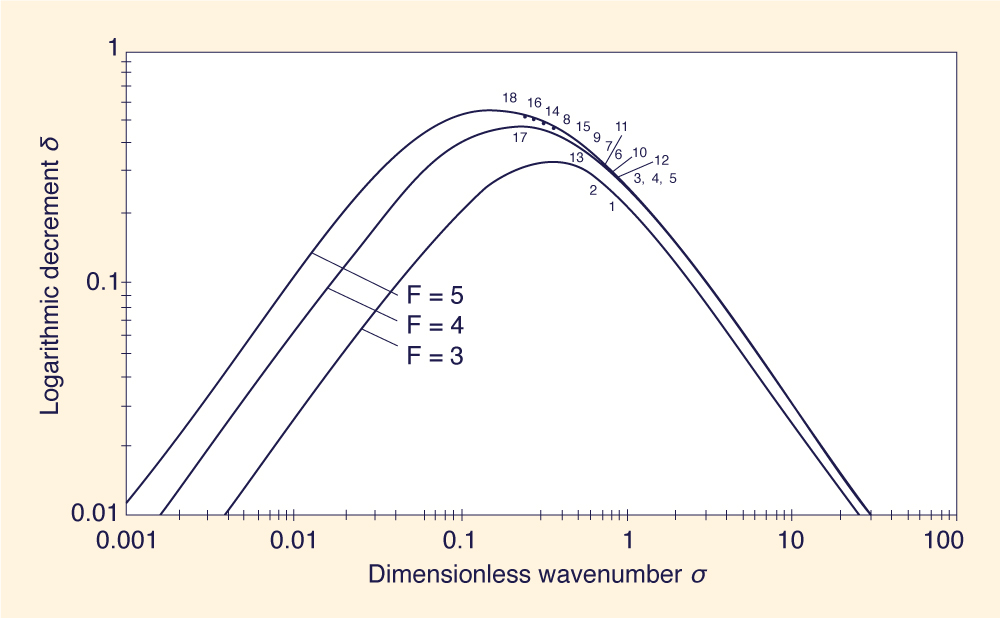
The solid curves of Figs. 1 and 2 show logarithmic decrement δ versus dimensionless wavenumber σ, (7), for the range of Froude numbers suited to this study. A total of 18 σ - F data points (3 < F < 5) obtained from the Brock data are shown in Fig. 1,
Ten (10) additional data points (5 < F < 8) are shown in Fig. 2. The agreement between theory and experiments is very good, considering the five order-of-magnitude range of possible dimensionless wavenumbers. This agreement is evidence that roll waves are likely to form within a narrow band of dimensionless wavenumbers, at or near the peak of the functional relation δ = f (σ), i.e, for values of the logarithmic decrement δ > 0.2.
5. SUMMARY
Using Brock's (1967) laboratory flume data, an experimental verification of a theory of roll-wave formation (Ponce and Simons 1977) was presented. Results show that dimensionless wavenumbers corresponding to the roll waves documented by Brock's study plot near the peak of the theoretical functional relation of logarithmic decrement δ versus dimensionless wavenumber σ.
APPENDIX |. REFERENCES
Brock, R. R. 1967. "Development of roll waves in open channels." Rep. No. KH. R-16, W. M. Keck Laboratory of Hydraulics and Water Resources, California institute of Technology, Pasadena. Calif.
Chow, V. T. 1959. Open-channel hydraulics, McGraw-Hill, New York, N.Y.
Craya, A. 1952. "The criterion of the possibility of roll wave formation." Gravity Waves, National Bureau of Standards Circular No. 521, National Bureau of Standards, Washington, D.C., 141-151.
lwasa, Y. 1954. "The criterion for the instability of steady uniform flows in open channels." Memoirs of the Faculty of Engineering, Kyoto University, Kyolo,Japan, 16(6),264-275.
Liggett, J. A. 1975. "Stability -Chapter 6," Unsteady flow in open channels, Vol. 1, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Fort Collins, Colo., 259-281.
Mayer, P. G. W. 1957. "A study of roll waves and slug flows in inclined open channels," PhD dissertation, Cornell University, Ithaca, N.Y.
Ponce, V. M., and D. B. Simons. 1977. "Shallow wave propagation in open channel flow." J. Hydr. Div., ASCE, 103(12), 1461-1476.
Ponce, V. M. 1991. "New perspective on the Vedernikov number," Water Resour. Res., 27(7), 1777-1779.
Vedernikov, V. V. 1945. "Conditions at the front of a translation wave disturbing a steady motion of a real fluid," U.S.S.R. Academy of Sciences Comptes Rendus (Doklady), 48(4), 239-242.
Vedernikov, V. V. 1946. "Characteristics features of a liquid flow in an open channel." U.S.S.R. Academy of Sciences Comptes Rendus (Doklady), 52(3), 207-210.
|
| 220610 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |