USING ONLINE CALCULATION
Rosa D. Aguilar
ACKNOWLEDGEMENTS
The completion of this thesis was possible through perseverance. The first time
I heard the word perseverance was in the 9th grade by a college counselor. What that meant for me was
that I was to overcome the statistics and stereotypes placed on kids coming out of inner city
schools. I got through every obstacle and discouragement experienced in high school, college, and
life after college simply with the hope for a better future.
Therefore, I thank Jesus Christ the Lord for his abundant love, patience, and grace. For the strength that I have to
persevere is given by Him through the Holy Spirit. I am thankful for His Word, for I know that in
it I can find the truth.
I thank my parents for the faith they were able to instill in me, for their unconditional love,
encouragement, and prayers. I thank my siblings for their love, support, and their constant willingness to make
me laugh. I would also like to express my gratitude to the Smith family for their love, support,
and cheerfulness.
Moreover, I would like to express my deepest gratitude to Dr. Victor M. Ponce, who placed in me his trust,
patience, and support throughout the development of this thesis, while helping me grow academically
and professionally. I have learned more than I could have ever dreamt of, and for that I am thankful.
My gratitude goes to Dr. Subrata Bhattacharjee and Dr. Luis Parra for their support in being part of my thesis
committee. Lastly, I would like to thank Dr. Levent Kavvas, Dr. Carlos Puente, and other mentors I have
had along the way, for their words of wisdom and encouragement to pursue my dreams.
1. INTRODUCTION
1.1 Background Mathematical models for the analysis of overland flow have been developed since the 1960s. The essential problem to be solved is to determine the flow off the plane at the downstream end, for given geometric, hydraulic, and hydrologic conditions (Dooge 1973). A commonly used method is the solution of the kinematic wave equations together with a simplified version of a catchment (Ponce 1986). The catchment is represented by an open-book configuration, in which two planes are adjacent to a channel. The concept of the kinematic wave is well established among the existing methods to solve unsteady, one-dimensional, gradually varied open-channel flow problems (Ponce 1991a). The kinematic wave assumes steady uniform flow and as such, the method lacks wave attenuation. While this simplification has been generally accepted, the diffusion wave model presents a method that better describes the physical characteristics of the catchment. The diffusion wave method for the analysis of overland flow assumes steady nonuniform flow, in which the flow depth gradient is a critical component of the solution. [The term "diffusion" is used in this thesis to refer to the diffusion of momentum, as oppose to that of mass or energy]. To a large extent, the flow depth gradient explains the naturally occurring diffusion in unsteady free surface flows (Ponce 1989). The diffusion wave uses physical properties to define physical diffusion, while the kinematic wave does not. The diffusion wave method can be applied to a wider range of problems because most flood waves in nature are subject to a small amount of attenuation. The diffusion wave method may be extended into the realm of dynamic waves by incorporating the Froude number dependence of the hydraulic diffusivity. The Froude number's relationship to the Vedernikov number is through the rating exponent β; thus, making the hydraulic diffusivity also a function of the Vedernikov number. The Vedernikov number makes possible the modeling of catchment dynamics using diffusion waves and including inertial effects, under a wide range of boundary friction and cross-sectional shape specifications (Ponce 1991b, Ponce and Huston 1994b).
The diffusion wave method is not only grid independent but also capable of minimizing numerical
dispersion. The diffusion wave model is based on the Muskingum-Cunge method with
lateral inflow (Cunge 1969; Ponce 1978, 1986), and capable of calculating the same results regardless of
the grid specification (Ponce 1979a). Grid independence, based on the Muskingum-Cunge
method, is
attained by matching the numerical diffusion of the discrete model with the
physical diffusion of the analytical model (Ponce and Chaganti 1994a). The diffusion wave
model sets the Courant number
1.2 Objectives The objective of this thesis is to develop an online diffusion wave model of catchment dynamics using an open-book configuration. The model is grid independent, capable of conserving volume, minimizes numerical dispersion, and extends into the realm of dynamic waves by incorporating the Vedernikov number into the hydraulic diffusivity. A significant aspect of a model is grid independence, allowing it to calculate the same results regardless of the grid size. The modeler should be able to run the model without the concern of choosing the correct grid size. The diffusion wave model is reliable and predictable, for it is capable of calculating the same peak flow regardless of the chosen time interval (within reason). An overland flow model that is capable of conserving volume is required for acceptable accuracy. The total effective rainfall volume, after all abstractions are taken into account, ought to be the same as the outflow hydrograph volume for a particular flood event. The volume cannot be lost or added, but rather it may be spread over the area or simply translated, such as the kinematic wave model. The diffusion wave model conserves the total effective rainfall volume. Minimizing numerical dispersion is a unique aspect of the diffusion wave model. The model reduces numerical dispersion by keeping the Courant number close to 1; thus, making the model results more accurate (Ponce 1979, 1986). The diffusion wave model extends into the realm of dynamic waves by including the Vedernikov number into the hydraulic diffusivity. Including the Vedernikov number makes the model capable of computing flood waves for a wider range of open-channel flow conditions. 1.3 Scope The development of the online diffusion wave model (ONLINE OVERLAND) is with the open source general-purpose scripting language Hypertext Processor (PHP), which is especially suited for web development, while embedded into HyperText Markup Language (HTML). The online calculation is accomplished with PHP while the input and output is designed using HTML. PHP carries out the computation while HTML displays the input and output online. Grid independence is tested by using different grid size resolutions (a) Δt = 3.75 min, (b) Δt = 7.5 min, and (c) Δt = 15 min. Grid independence for the diffusion wave model is compared to the kinematic wave model similar to the one proposed by Li et al. (1975). The model is tested for volume conservation by varying the following parameters:
Moreover, numerical dispersion is minimized by adjusting
the grid size ratio such that the Courant number
2. THEORETICAL BACKGROUND
2.1 Historical Perspective Over the years, many attempts have been made to develop models for the analysis of overland flow. This challenge has been undertaken by many engineers, mathematicians and scientists, who have contributed to the solution of overland flow. The essential problem to be solved is to determine the flow off the plane at the downstream end for given physical conditions and a given pattern of lateral inflow along the plane (Dooge 1973). Accumulation of excess rainfall allows for water to flow out of the plane; however, equilibrium conditions can be attained if rainfall excess continues and water begins to pond on the plane such that inflow is equal to outflow. Once rainfall excess ceases, equilibrium conditions are lost, water continues to flow out of the plane, and stored volume begins to deplete back to zero (Ponce 1989). The St. Venant equations (Ponce 1989) describe the motion of water in overland flow. These are the equation of continuity (Eq. 2.1) and the equation of motion (Eq. 2.2):
in which q = flow rate per unit width, y = depth of flow, i = lateral inflow (excess rainfall), u = velocity, g = acceleration due to gravity, So = bottom slope, Sf = friction slope. These are partial differential equations; however, the nonlinearity of the equation of motion has defied the search for a solution. The equation of motion is a function of inertia, pressure gradient, friction, gravity and momentum-source term. Overland flow modeling has been attempted by Horton (1938), Izzard (1944), Lighthill and Whitham (1955), Schaake (1965), Wooding (1965), Woolhiser and Liggett (1967), Dooge (1973), and Ponce (1986). These authors have simplified the equation of motion to determine an approximation of the behavior of overland flow. The kinematic wave and diffusion waves have been used to obtain a simplified solution to the overland flow problem. Surface runoff is studied in reference to soil erosion by Horton (1938). In his paper, he explains that in order for surface runoff to occur, there must be a rainfall excess or the difference between rainfall and infiltration. Moreover, that all existing depressions must be filled to overflow levels. This suggests that there is a relationship between runoff intensity and depth of surface detention. This relationship, as expressed by Horton, is simply a power function (Eq. 2.3):
In which qs = runoff intensity, Ks = constant dependent on the characteristics of the area, δ = depth of surface detention along the stream margin, and M = an exponent on the type of overland flow. Equation 3 is a storage equation which relates net supply, surface detention and surface runoff. Izzard (1944) applied the equation of motion (Eq. 2.2) to experimental data of paved surfaces under equilibrium conditions, that is, the data does not include flow from the rising or falling limbs of the hydrograph. From the studies, Izzard concluded that the upper end of the surface profile is independent of the overland flow length; thus, it is appropriate to use detention data for various lengths to develop a relationship between detention and discharge. Lighthill and Whitham (1955) introduced the kinematic wave concept, where the solution arises on the equation of continuity (Eq. 2.1). The kinematic wave describes the convection of a quantity. Since the convection equation is of first order, the kinematic wave has only one wave velocity. This wave velocity is described by Seddon's law (Eq. 2.4):
in which B = the local breadth or width of the river. Schaake (1965) presented a method for synthesizing the hydrograph for paved surfaces in a watershed. The rainfall-runoff process consists of infiltration, depression storage and surface runoff. Schaake explains that the synthetic unit hydrograph must be obtained from knowledge of the physical features of the area. To describe the mechanics of surface runoff, the equations of gradually varied unsteady flow in open channels (Eq. 2.1 and 2.2) were used. The drainage area was divided into small component parts where the equations of motion were applied to describe each component. The solution to the equations was obtained using the finite-difference method. Outflow from one component becomes inflow for the next, which ultimately represents the overland flow of the entire area. Schaake's results agreed with those of Izzard. Wooding (1965) presented an analytical solution for the hydraulic model by the method of characteristics. The rainfall and infiltration are uniformly distributed over the entire catchment. The catchment is presented as two rectangular planes joined together to form a V-shape at which a stream flows and the main characteristics of a catchment are to be preserved (slope, roughness and flow regime). Wooding's solution is presented as the kinematic wave approximation to the equations of motion: the continuity equation (Eq. 2.1) and the momentum equation is reduced to a depth-discharge relationship similar to that of Horton's storage equation (Eq. 2.3). Woolhiser and Liggett (1967) used a dimensionless approach to developing a solution to equations (2.1) and (2.2). They integrated the governing equations using the finite-difference method. Comparison with previously performed calculations led to the discovery that there is no particular rising hydrograph for overland flow, and that the kinematic wave solution was, for the most part, an accurate solution to the overland flow problem. Woolhiser and Liggett found that a dimensionless parameter k (Eq. 2.5) was a suitable criterion for the choice between the complete equations or the kinematic wave approximation in which the effects of the length and slope of the plane (channel) can be related.
in which So = bottom slope, Lo = length of the plane (channel), Ho = normal depth and Fo = Froude number for normal depth. The objective of the studies presented by Woolhiser and Liggett was to determine the effects of the dimensionless parameters k and Fo on the hydrographs. The solutions were compared to that of the kinematic wave solution and the 1946 experimental results of Izzard. When compared to the kinematic wave solutions, the results showed that for values greater than 10 for parameter k, the kinematic wave solution was a good approximation (Woolhiser and Liggett 1967). Dooge (1973) compiled several solutions to overland flow, including that of Horton-Izzard, kinematic wave, and Woolhiser and Liggett. The Horton-Izzard approach to the solution of overland flow modeling is accomplished by replacing the equation of motion by an outflow-storage relationship. This solution was first applied to natural catchments by Horton and later applied to paved surfaces by Izzard. The assumption of this method is that the solution to the whole system is lumped together and treated as a single nonlinear reservoir. The kinematic wave solution, on the other hand, is not a lumped solution but rather is distributed at each point in which a relationship between the flow depth and discharge can be made. The assumption of the kinematic wave technique to solve the overland flow problem is that all components of the momentum equation are negligible compared to the bottom slope and friction slope (Dooge 1973). Ponce (1986) presented a solution to the equations of motion for modeling of catchment dynamics which has better convergence properties than the kinematic wave models. Ponce's solution is the diffusion wave method which matches physical and numerical diffusivities. This allows for full control of the numerical diffusion while featuring grid independence. The model is stable and convergent for values of Courant number (Eq. 2.6) close to 1. The Courant number is defined as follows:
In which c = physical celerity, and Δs/Δt = grid celerity. The diffusion wave method presented here is independent of grid size; that is, that a coarser grid size resolution (within reason) can be used and the solution will still converge. Orlandini and Rosso (1996) presented a solution to overland flow using the diffusion wave model, following the model of Ponce (1986). The Muskingum-Cunge method of variable parameters was used to describe the flow dynamics and a digital elevation model (DEM) was used to capture the topography and river network structure on storm-flow. The results obtained through this method provided 98% mass conservation. Moreover, it was shown that the model was accurate for a wide range of slopes and roughness characteristics, space and time intervals, and rainfall excess forcing rates. 2.2 Wave Models The solution to the equations of motion (Eq. 2.1 and 2.2) can be obtained from the full dynamic wave method, which is the most accurate representation of free-surface flow. The full dynamic wave solution to overland flow modeling includes all the terms of the momentum equation: inertia, pressure gradient, friction, gravity and momentum-source term. The full dynamic wave solution does not require linearization; however, it is complex and failure-prone. An alternative is to resort to various simplifications of the full equations, in the interest of practicality and/or mathematical tractability (Ponce 1989). Simplifying the equations, linearizing, and combining into one equation gives rise to three different methods: (1) kinematic wave, (2) diffusion wave, and (3) diffusion wave with dynamic component, herein referred to as dynamic wave. Kinematic waves are the most simplified type of wave; dynamic waves are the most complete. Diffusion waves lie somewhere in between kinematic and dynamic waves (Ponce 1989). 2.3 Kinematic Wave Modeling The kinematic wave is obtained from the equation of continuity and the assumption of uniform flow; thus, the momentum equation reduces to a balance of only gravitational and frictional forces. The assumption of uniform flow reduces the applicability of the kinematic wave. The equation of continuity states that the quantity in a small element of length changes in time at a rate equal to the difference between inflow and outflow (Lighthill and Whitham 1955). Uniform flow in open channels is described by the Manning equation:
in which n = Manning's roughness coefficient, A = flow area, R = hydraulic radius, and Sf = friction slope. The kinematic wave equation is obtained by multiplying the equation of continuity times the wave celerity (Ponce 1989):
in which βV = wave celerity. In general, wave celerity varies with discharge, making Eq. 2.8 nonlinear (quasilinear). In practice, a constant wave celerity may be assumed and the equation can be solved by analytical and numerical means. A numerical solution for Eq. 2.8 can be derived using a first-order-accurate numerical scheme, in which backward differences is used for both spatial and temporal derivatives. Using this scheme, the following routing equation is obtained (Ponce 1989):
in which
This first-order numerical scheme is stable for all Courant numbers, but generates a substantial amount of numerical diffusion. An alternative is another solution to Eq. 2.8 obtained by applying two first-order schemes, which are stable for Courant numbers C ≥ 1 and C ≤ 1, alternatively. The first scheme (Scheme I) is a forward-in-time, backward-in-space solution, stable for Courant numbers C ≤ 1. The second scheme (Scheme II) is a forward-in-space, backward-in-time solution, stable for Courant numbers C ≥ 1 (Ponce 1989). The routing equation for Scheme I is defined as:
in which
The routing equation for Scheme II is:
in which
The accuracy of these two schemes is contingent upon the Courant number being equal to or close to 1. In this case, the schemes simulate the kinematic wave equation. If the Courant number differs substantially from 1, these two numerical schemes introduce sizable amounts of numerical diffusion. The latter is physically unconfirmed, and at odds with the true physical diffusion (if any) of the physical problem. Thus, for catchments experiencing small amounts of physical diffusion, the flow is likely to be better modeled with the diffusion wave.
2.4 Diffusion Wave Modeling Diffusion wave modeling is an improvement to kinematic wave modeling due to the addition of the flow depth gradient of the equation of motion. To a large extent, the flow depth gradient explains the naturally occurring diffusion in unsteady free surface flows (Ponce 1989). The derivation of the diffusion wave equation is obtained from the assumption of steady nonuniform flow (friction slope is equal to water surface slope). Unsteady flow using the diffusion wave method is defined by:
in which So - (dy/dx) is the water surface slope and dy/dx represents the flow-depth gradient. From the continuity equation and the assumption of steady nonuniform flow, the diffusion wave equation is derived (Ponce 1989):
in which the left-hand side of Eq. 2.19 is the kinematic wave equation, while the partial derivative term of the right-hand side is the second-order term which describes physical diffusion. The coefficient of the second-order term accounts for the channel diffusivity:
in which
and D is a type of cell Reynolds number, defined as a ratio of physical diffusivity to numerical diffusivity:
The diffusion wave uses physical properties to define physical diffusion, while the kinematic wave does not. The diffusion wave method can be applied to a wider range of problems because most floods waves in nature are subject to a small amount of attenuation. 2.5 Dynamic Wave Modeling The diffusion wave model can be further improved to include the dynamics of the wave phenomena (Ponce 1986). The diffusion with dynamic component incorporates the Froude number dependence of the hydraulic diffusivity (Eq. 2.20). Dooge (1973) introduced this concept for hydraulically wide channels under Chezy conditions (β = 3/2), and further expanded by Ponce (1986). The modified hydraulic diffusivity is expressed as:
Likewise, the cell Reynolds number (Eq. 2.26) can be modified to account for the Froude number dependence of the physical diffusivity (Ponce 1986):
Moreover, since the Vedernikov number is (Ponce 1991b):
The hydraulic diffusivity reduces to:
and the cell Reynolds number to:
With the hydraulic diffusivity and cell Reynolds number thus defined, the wave dynamics can be effectively incorporated into an overland flow solution. The Vedernikov number is shown to characterize unsteady free-surface flows for a wide range of boundary friction and cross-sectional shape conditions (Ponce 1991b, Ponce and Huston 1994b). Therefore, Eqs. 30 and 31 are particularly useful for flow conditions in which the Vedernikov number is substantially different than zero (Ponce 1986, 1991b).
3. MODEL DESCRIPTION
3.1 Model Features The online diffusion wave model uses a simplified spatial representation of a catchment in which two rectangular planes are adjacent to a channel in the form of an open-book (Wooding 1965; Ponce 1986). The diffusion wave model is shown to have better convergence properties than alternative kinematic wave models. A significant feature of the diffusion wave model is its grid independence, allowing it to calculate essentially the same results, regardless of the grid specification. The only grid input is the time interval Δt. Upon execution, the program adjusts the value of the space interval Δx in planes and channel to assure grid independence and preserve modeling accuracy. This correct numerical behavior is due to the fact that the diffusion wave model matches the physical diffusivity with the numerical diffusivity (Ponce et al. 1979b). In addition, the model minimizes numerical dispersion by adjusting the grid ratio such that the Courant number C = 1. This leads to a simulation that is as numerically and physically accurate as it is possible under the open-book schematization. The specification of the dynamic hydraulic diffusivity, replacing the kinematic hydraulic diffusivity, extends the diffusion wave model to the realm of dynamic waves (Ponce 1991b). This assures the physical accuracy of the overland flow model through a wide range of Vedernikov numbers. 3.2 Model Components ONLINE OVERLAND is a physically based model of overland flow, which simulates catchment dynamics using the diffusion wave. The model requires the input of physical parameters and flow characteristics of both the planes and the channel. ONLINE OVERLAND is capable of running SI (metric) or U.S. Customary units, selected at the beginning of data input. The model has the following components:
3.3 Hydrologic Abstraction ONLINE OVERLAND uses the USDA NRCS runoff curve number method for hydrologic abstraction. The effective runoff depth is a function of total rainfall depth and curve number CN, which is the abstraction parameter. The chosen curve number is a function of: (1) soil type, (2) land use and treatment, (3) ground surface condition, and (4) antecedent moisture condition. The effective rainfall depth Q is calculated by subtracting the hydrologic abstraction from the total rainfall depth P (Ponce 1989). The method is based on the following proportionality between retention and runoff:
Equation 33 is improved by subtracting the total rainfall depth by an initial abstraction Ia. Solving for the effective rainfall depth Q leads to the following equation:
in which Eq. 3.3 is physically restricted to the condition P ≥ Ia. The standard initial abstraction Ia is:
With Eq. 3.4, Eq. 3.3 reduces to:
in which Eq. 3.5 is restricted to P ≥ 0.2S, and S is the maximum potential retention (in inches):
The effective rainfall depth Q is expressed in terms of CN :
in which Eq. 3.7 is restricted to values of P ≥ (200/CN - 2), and P and Q are given in inches. In SI units, the equation is:
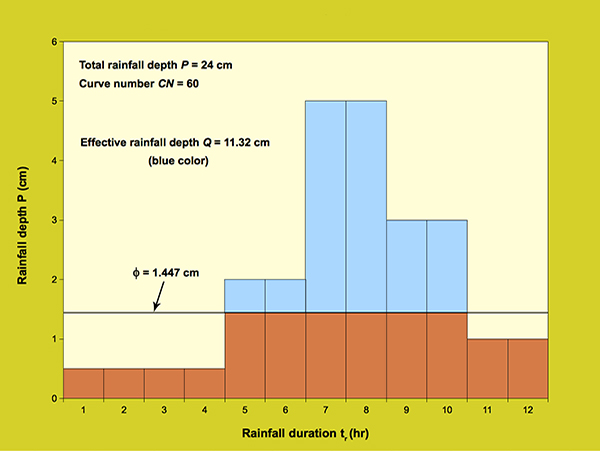
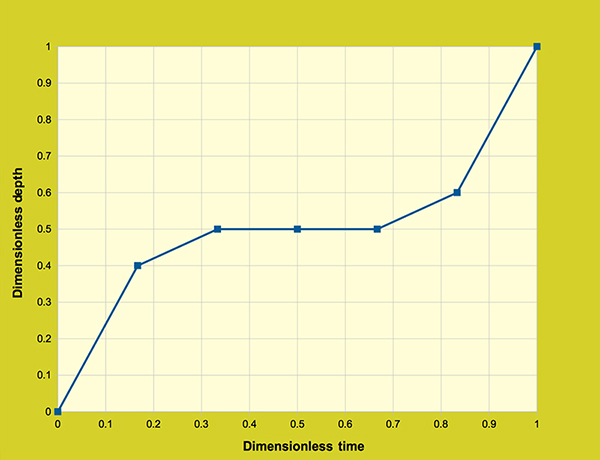
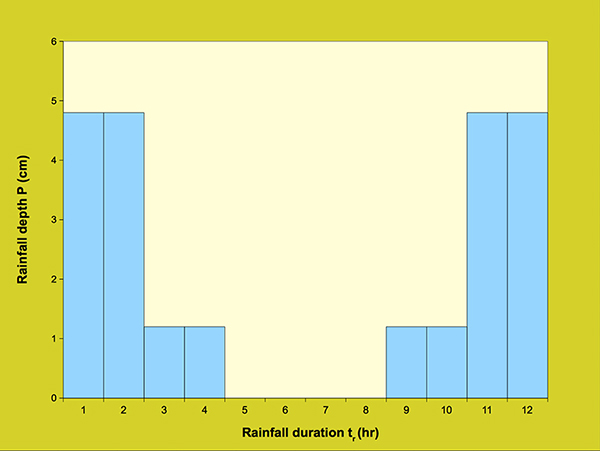
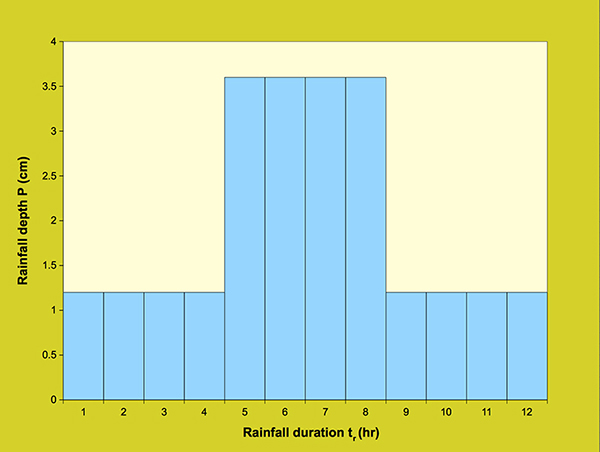
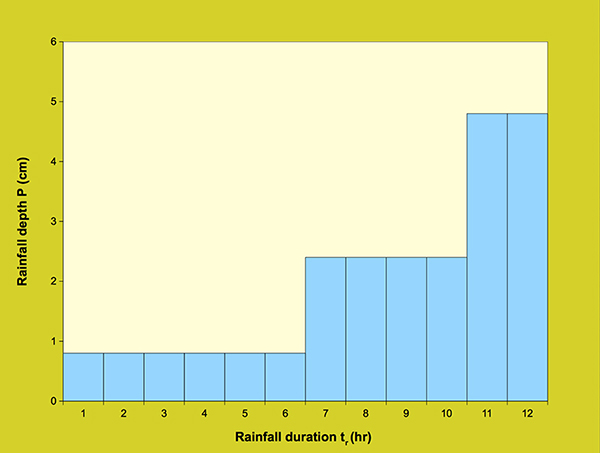
in which Eq. 3.8 is restricted to values of P ≥ R [(200/CN) - 2]. With R = 2.54 in Eq. 3.8, P and Q are given in centimeters. For a uniform rainfall distribution, the calculation of effective rainfall by using the runoff curve number method is straightforward. With P and CN, a value of Q can be calculated from Eq. 3.7 or 3.8. For a nonuniform rainfall distribution, the calculation of effective rainfall is performed by using the concept of the φ-index. The φ-index is defined as the constant infiltration rate to be subtracted from the prevailing rainfall rate in order to obtain the runoff volume that actually occurred. In ONLINE OVERLAND, the calculation of φ-index is performed by trial-and-error. For example, for a 24 cm rainfall depth with a curve number CN = 60, the calculated effective rainfall depth is 11.32 cm (Eq. 3.7). With a total rainfall duration of 12 hours, and the rainfall distribution shown in Table 3.3.1 and Figure 3.3.1, the φ-index value, calculated by trial-and-error, is: φ = 1.447 cm. The effective rainfall hyetograph is shown in light blue color in Figure 3.3.2.
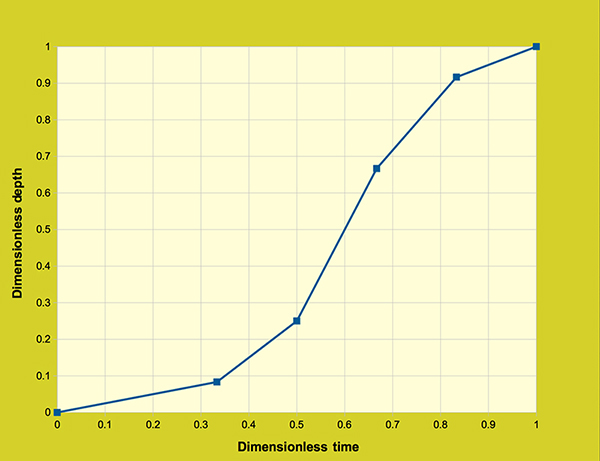
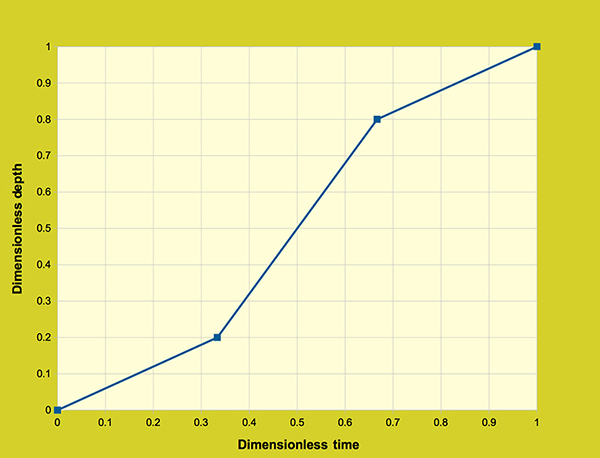
Figure 3.3.1. Dimensionless cumulative rainfall distribution.
Figure 3.3.2. Calculation of effective rainfall hyetograph by the φ-index method.
3.4 Input Description The following input values are described here in detail.
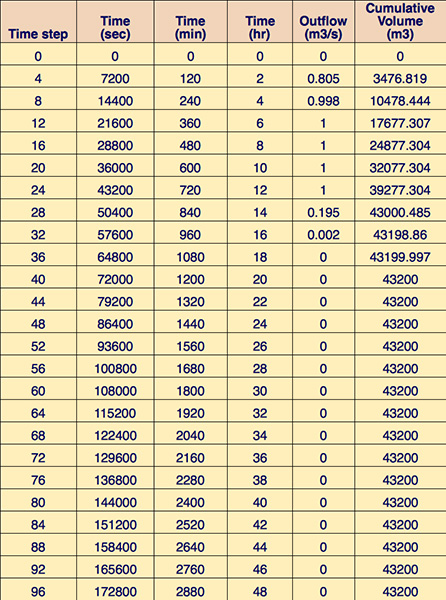
3.5 Output Description ONLINE OVERLAND uses the input values described in Section 3.4 to calculate the outflow and cumulative volume for each time step, shown in a table format. The output table prints the Time step, Time in seconds (sec), minutes (min), and hours (hr), Outflow in m3/s for SI units and cfs for U.S. Customary units, and the Cumulative Volume in m3 for SI units and ft3 for U.S. Customary units. Figure 3.5.1 is an example of an output table produced by ONLINE OVERLAND in SI units, using a number of time intervals for printing NΔt = 4.
Figure 3.5.1. Diffusion wave overland flow model output table.
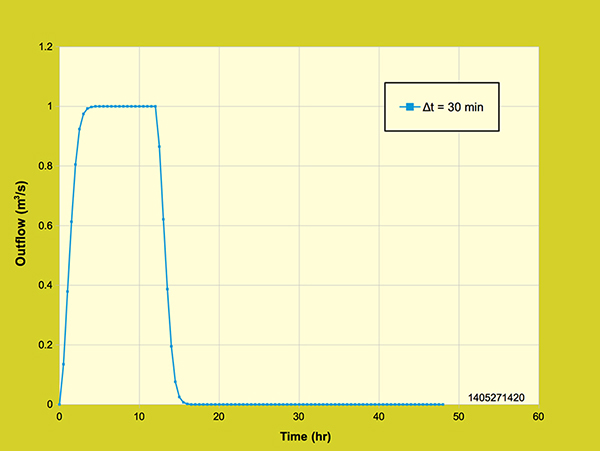
The outflow hydrograph can then be produced using a spreadsheet by plotting Time (hr) vs
Outflow (m3/s), using
Figure 3.5.2. Diffusion wave overland flow model outflow hydrograph.
4. ONLINE DEVELOPMENT
4.1 Rationale The simulation of catchment dynamics using a physically based overland flow model is well established in hydraulic and hydrologic engineering practice (Ponce 1986). The kinematic wave model is widely used in well established modeling software; however, it lacks grid independence. The diffusion wave model, on the contrary, is an improvement over the kinematic wave model because it is grid independent. Moreover, unlike the kinematic wave model, the diffusion wave model is capable of generating an outflow hydrograph that does not vary with the choice of grid size. Grid independence is due to the fact that the diffusion wave model matches the physical diffusivity of Hayami with the numerical diffusivity of Cunge (Ponce et al. 1979b). In addition to matching diffusivities, ONLINE OVERLAND minimizes numerical dispersion by specifying the grid ratio such that the Courant number is equal to 1. This leads to a simulation that is as numerically and physically accurate as it is possible under the open-book schematization. The diffusion wave model is further improved by showing that the hydraulic diffusivity is a function of the Froude number, therefore, the Vedernikov number (Ponce and Huston 1994b). The kinematic wave hydraulic diffusivity is thus replaced, and the diffusion wave model is extended to the realm of dynamic waves (Ponce 1991b). This assures the physical accuracy of the overland flow model through a wide range of Vedernikov numbers.
ONLINE OVERLAND uses the diffusion wave model
to calculate overland flow in an open-book schematization, using one book.
The appropriate specification of Courant number and
dynamic hydraulic diffusivity assures
a simulation that is as physically and numerically accurate as it is
possible in deterministic catchment modeling. 4.2 Language ONLINE OVERLAND was developed with the open source general-purpose scripting language Hypertext Processor (PHP), which is especially suited for web development, while embedded into HyperText Markup Language (HTML).
PHP was developed in 1994 by Rasmus Lerdorf, and it was originally written in the C programming language. PHP
has since developed into a scripting language based on C, Java, and Perl. The scripts can be used with server-side
scripting, requiring a PHP parser, a web server, and a web browser. The PHP code is analyzed using the PHP parser,
and the server makes the output viewable on the web page in the web browser. Scripts can also be used with command
line scripting, in which a server and web browser are not required to execute the code, but simply the PHP parser.
Lastly, another main usage of PHP scripts is to write desktop applications. While PHP is not the ideal language
to create desktop applications with a graphical user interface, advanced knowledge of PHP with GNU Image
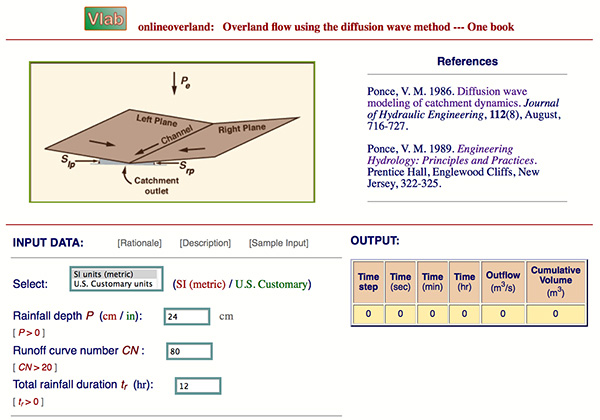
Manipulation Program (GIMP) Toolkit (PHP-GTK) would make the writing of these programs possible PHP files are capable of interpreting both PHP and HTML code; thus, allowing the files to swap between languages. Once the PHP code is executed on the server, an HTML file is then generated to be viewed by the user while concealing the code. In addition to the mentioned output, PHP can also output images, PDF files and Flash movies, all generated on the fly (Achour 2014). The input cells in ONLINE OVERLAND were developed using HTML as shown partially in Figure 4.2.1. PHP interprets the input values and runs the code to compute the Outflow and Cumulative Volume. The output table displayed was also developed using HTML, in which it is capable of interpreting the PHP calculated output and making it easy to view in a table format, also shown in Figure 4.2.1.
Figure 4.2.1. ONLINE OVERLAND data input and output table.
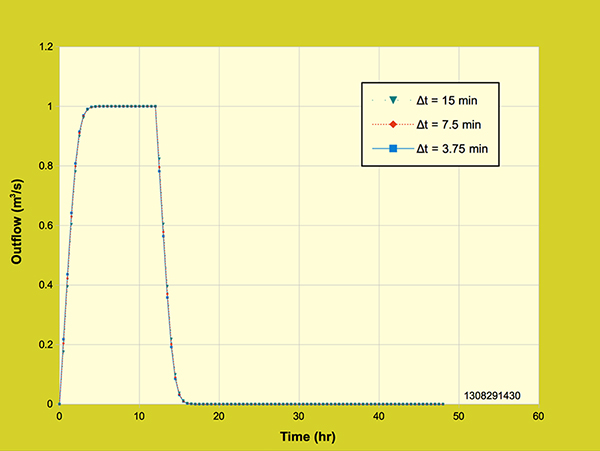
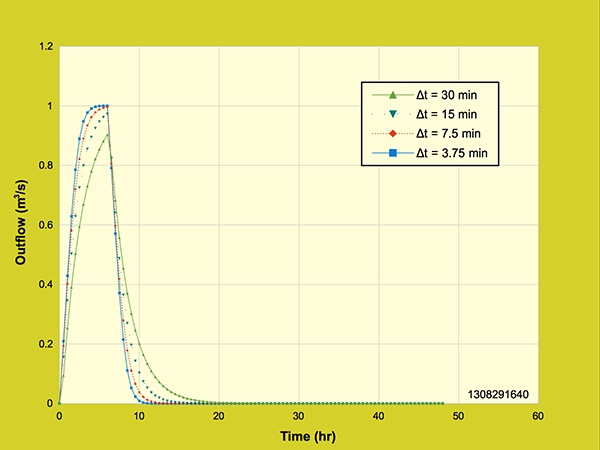
4.3 Grid Independence Grid independence is described as the ability of a numerical model to provide the same results, regardless of grid size. A model that is grid independent through a wide range of grid sizes is considered to be a good model, i.e., one that minimizes numerical diffusion and dispersion. In this section, the performance of the diffusion wave model is compared with that of the backward-in-time/backward-in-space kinematic wave model due to Li et al. (1975). Figure 4.3.1. shows three outflow hydrographs generated with the diffusion wave model using three different grid configurations.
Figure 4.3.1. Diffusion wave model: Effect of grid resolution on the outflow hydrograph,
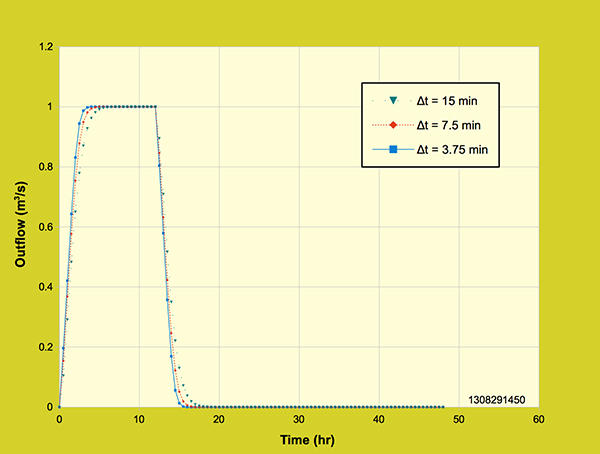
A significant feature of the diffusion wave model is that it sets the space interval in such a way that the Courant number is always equal to 1, optimizing numerical diffusion while minimizing numerical dispersion. This figure shows the effect of grid size on the outflow hydrograph. For this example, the effective rainfall depth is specified as Pe = 24 cm; the rainfall duration is tr = 12-hr; therefore, the effective rainfall intensity ie = 2 cm/hr. The drainage area is A = 18-ha. For these conditions, the peak flow is: Qp = ie A = 1 m3/s. The three calculated outflow hydrographs correspond to the time intervals Δt = 15, 7.5, and 3.75 min, respectively. The hydrographs are shown to be essentially the same, confirming the grid independence of the diffusion wave model. For purposes of comparison, Figure 4.3.2. shows three outflow hydrographs generated with a kinematic wave model that uses backward-in-space/backward-in-time differences, while keeping the Courant number equal to 1.
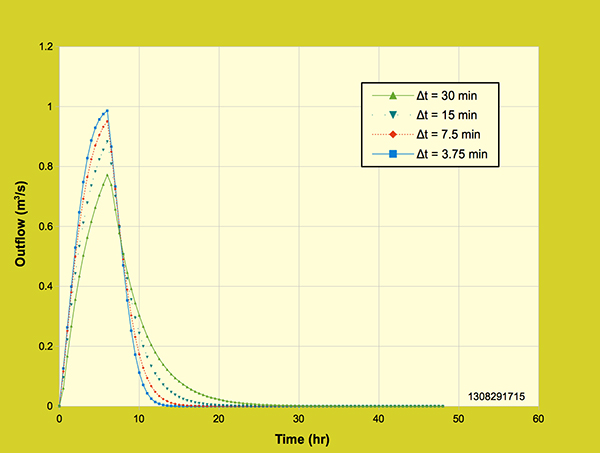
Figure 4.3.2. Li et al Model: Effect of grid resolution on the outflow hydrograph,
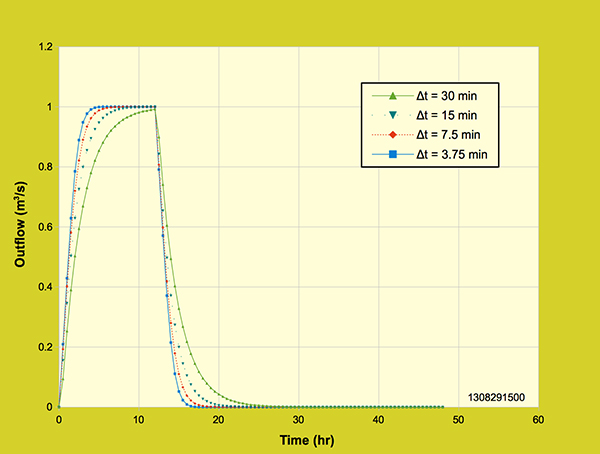
The general formulation of this model is described by Ponce (1989), following Li et al. (1975). Unlike the diffusion wave model, Figure 4.3.2. shows that the Li et al. model is slightly sensitive to the grid size. Figure 4.3.3 shows four outflow hydrographs generated with a backward-in-space/backward-in-time model that specifies both time interval Δt and space interval Δx as input, which effectively renders the Courant numbers on planes and channel different than 1.
Figure 4.3.3. Li Two Model: Effect of grid resolution on the outflow hydrograph,
Unlike the previous two models that were based on Courant numbers being equal to 1, Figure 4.3.3 shows that this third model is markedly sensitive to the grid size, defying grid independence. The lack of grid independence is made more apparent when the rainfall depth is reduced from 24 cm to 12 cm, and the rainfall duration is reduced from 12-hr to 6-hr, while keeping the same effective rainfall intensity of 2 cm/hr, as shown in Figure 4.3.4.
Figure 4.3.4. Li Two Model: Effect of grid resolution on the outflow hydrograph,
The effect of watershed size on the grid independence of the diffusion wave and Li et al models was tested by cutting in half the rainfall intensity while doubling the overland flow area. The effective rainfall depth was specified as 6 cm and the rainfall duration as 6-hr, i.e., an effective rainfall intensity of 1 cm/hr. The overland flow area was increased to 36-ha, thus maintaining a peak flow of 1 m3/s. Figure 4.3.5 shows four outflow hydrographs generated with the Li et al model, showing substantial grid dependence.
Figure 4.3.5. Li Two Model: Effect of grid resolution on the outflow hydrograph,
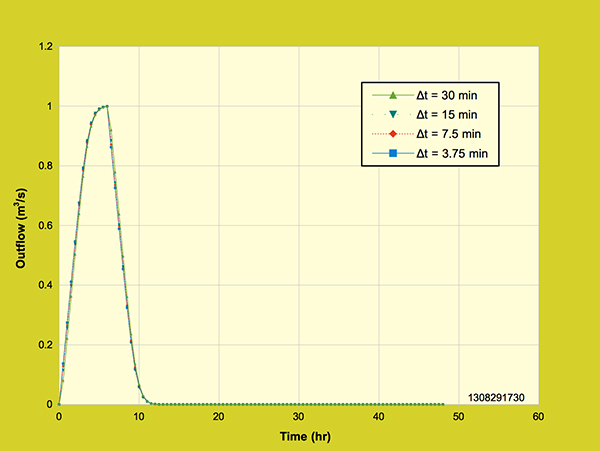
On the other hand, Figure 4.3.6 shows three outflow hydrographs generated with the diffusion wave model, showing essentially the same results, regardless of grid size.
Figure 4.3.6. Diffusion wave model: Effect of grid resolution on the outflow hydrograph,
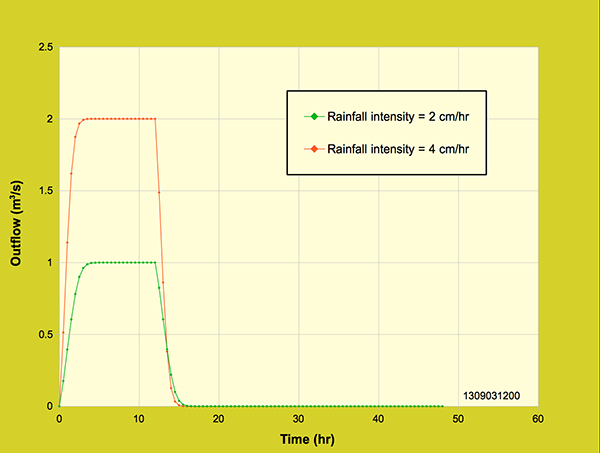
Thus, it is concluded that the diffusion wave model features grid independence through a wide range of grid sizes, unlike the backward-in-space/backward-in-time kinematic wave model, which does not. This is due to the proper specification of physical and numerical parameters in the diffusion wave model. Effectively, the diffusion wave model is physically responsive to the input bottom slopes, while in fact the kinematic wave model does not include bottom slope as input. 4.4 Script Testing Testing of the diffusion wave model was accomplished by varying several parameters, to examine the behavior and sensitivity of the model to these parameters. The parameters were: (1) rainfall intensity, (2) rainfall duration, (3) overland flow area, (4) fraction of area on the left plane, (5) reference discharge fraction, (6) rating exponent β, (7) bottom slope, (8) curve number, and (9) cumulative rainfall distribution. The effect of rainfall intensity was tested by running the model for two different rainfall intensities while maintaining the rest of the parameters constant. Figure 4.4.1 compares two hydrographs with rainfall intensities of 2 cm/hr and 4 cm/hr, for a 12-hr duration and a watershed area of 18-ha. As expected, the peak outflow for the rainfall intensity of 4 cm/hr is twice as large as that corresponding to 2 cm/hr. Likewise, the hydrograph volume for the rainfall intensity of 4 cm/hr is twice as large as that of the 2 cm/hr.
Figure 4.4.1. Diffusion wave model: Effect of rainfall intensity on the outflow hydrograph,
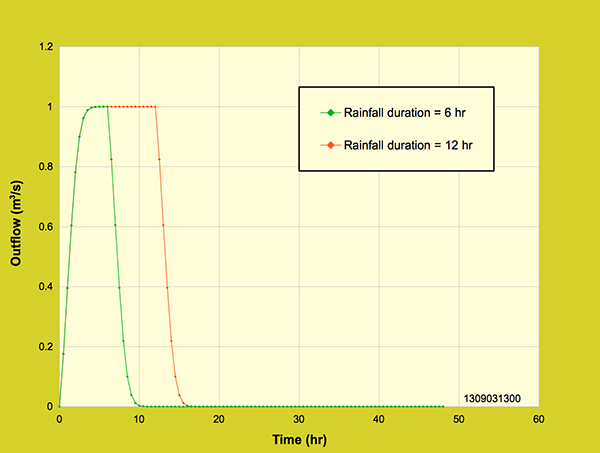
Figure 4.4.2 shows the outflow hydrographs for two rainfall durations, having the same intensity of 2 cm/hr and a watershed area of 18-ha. The rainfall durations are 6-hr and 12-hr. The peak outflow is the same, while the hydrograph volume for the 12-hr duration is twice as large as that of the 6-hr duration.
Figure 4.4.2. Diffusion wave model: Effect of rainfall duration on the outflow hydrograph,
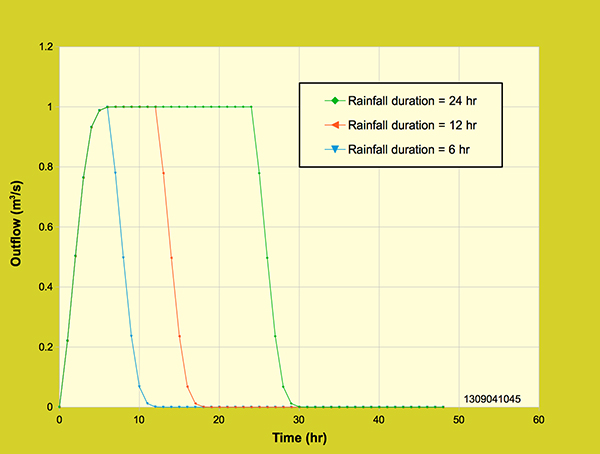
Figure 4.4.3 shows the outflow hydrographs for three rainfall durations, having the same intensity of 1 cm/hr and a watershed area of 36-ha. The rainfall durations are 6-hr, 12-hr, and 24-hr. The peak outflow is the same, while the hydrograph volume for the 12-hr duration is twice as large as that of the 6-hr duration, and the hydrograph volume for the 24-hr duration is twice as large as that of the 12-hr duration.
Figure 4.4.3. Diffusion wave model: Effect of rainfall duration on the outflow hydrograph,
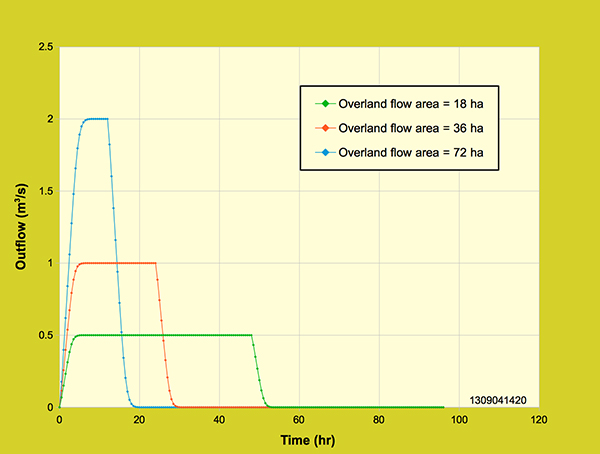
The effect of overland flow area was tested by running the model for three watershed areas while maintaining a constant rainfall intensity and rainfall volume. The watershed areas are 18-ha, 36-ha and 72-ha, with a rainfall intensity of 1 cm/hr and a rainfall volume of 86,400 m3. Figure 4.4.4 shows three outflow hydrographs for the three watershed areas. It is observed that the volume remains constant for all three hydrographs. The volume was preserved by reducing the rainfall depth and duration as the watershed area increased correspondingly. For the 36-ha area, a constant rainfall intensity (1 cm/hr) and volume (86,400 m3/s) results in a peak outflow which is twice as large as that of the 18-ha area. Likewise, the peak outflow for the 72-ha area is twice as large as that of the 36-ha area.
Figure 4.4.4. Diffusion wave model: Effect of overland flow area on the outflow hydrograph,
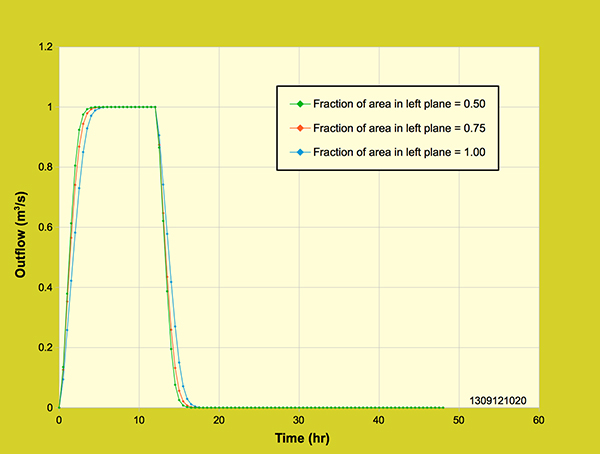
Figure 4.4.5 shows the effect of the fraction of area in the left plane on the outflow hydrograph. Three fractions are considered: 0.5, 0.75 and 1.00. The rainfall depth (24 cm) and effective rainfall duration (12-hr) were kept constant. It is seen that the hydrographs have the same peak outflow of 1 m3/s and the same volume of 43,200 m3, regardless of the contribution from the left plane. However, the timing of the hydrograph response varies with the contribution from the left plane. As expected, the response from the 0.5 fraction is faster than that of the 0.75 fraction, and the response of the 0.75 fraction is faster than that of the 1.00 fraction.
Figure 4.4.5. Diffusion wave model: Effect of fraction of area on the outflow hydrograph,
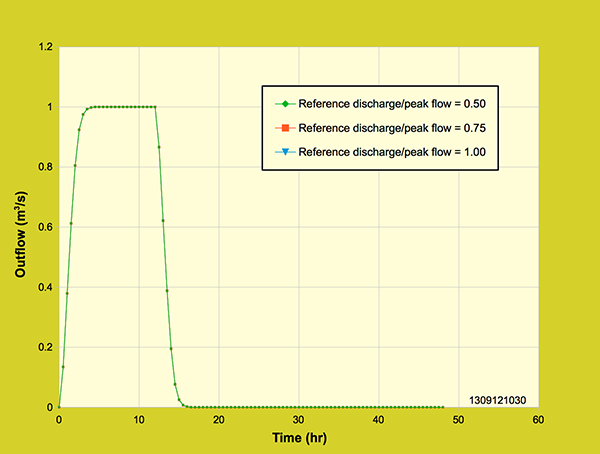
The model was tested on the fraction of peak flow used to estimate reference discharge. The fractions used are 0.5, 0.75 and 1.00, while the rainfall intensity (2 cm/hr) remained constant by keeping the rainfall depth and rainfall duration constant. Figure 4.4.6 shows that the three outflow hydrographs are essentially the same, having the same peak outflow (1 m3/s) and the same volume (43,200 m3). This test confirms that the results do not vary with the choice of reference discharge fraction, at least for this example of a relatively small watershed (18-ha).
Figure 4.4.6. Diffusion wave model: Effect of reference discharge fraction on the outflow hydrograph,
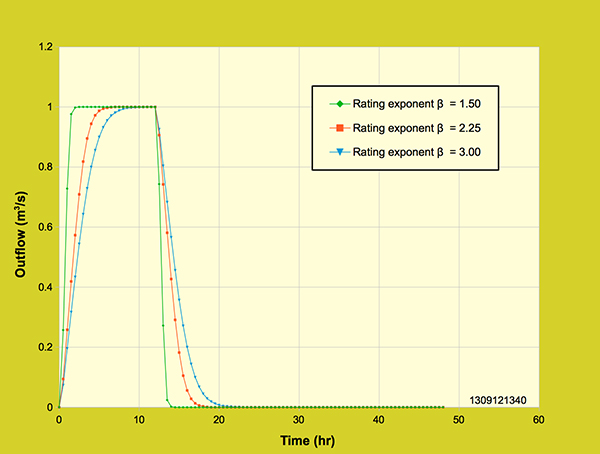
The effect of the rating exponent, β, was tested by running the model for three different values of β while maintaining a constant rainfall intensity and rainfall volume. Figure 4.4.7 shows three outflow hydrographs for the following three values of β: β:= 1.50 for turbulent flow, β = 2.25 for transitional flow and β = 3.00 for laminar flow. The hydrographs have the same peak outflow (1 m3/s) and volume (43,200 m3) regardless of the value of β. The timing of the hydrograph response varies with β. As expected, the response of the turbulent flow case (β = 1.50) is faster than that of the transitional flow (β = 2.25); likewise, the response of the transitional flow is faster than that of the laminar flow (β = 3.00).
Figure 4.4.7. Diffusion wave model: Effect of rating exponent β on the outflow hydrograph,
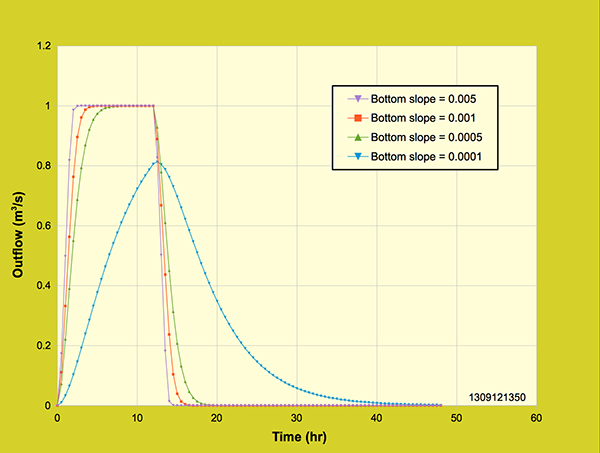
Figure 4.4.8 shows the effect of bottom slope on the outflow hydrograph. For these runs, the slopes used were 0.005, 0.001, 0.0005 and 0.0001 on planes and channel, while the rainfall intensity (2 cm/hr) and watershed area (18-ha) remained constant, corresponding to a maximum peak outflow of 1 m3/s. All four outflow hydrographs conserved volume (43,200 m3). The outflow hydrographs for the first three slopes (0.005, 0.001 and 0.0005) reached the maximum peak outflow. However, the fourth outflow hydrograph (0.0001) did not reach the maximum peak outflow at the end of rainfall (12-hr). As expected, all four outflow hydrographs show clearly the effect of bottom slope, that is, the hydrograph response slows down with a decrease in slope.
Figure 4.4.8. Diffusion wave model: Effect of bottom slope on the outflow hydrograph,
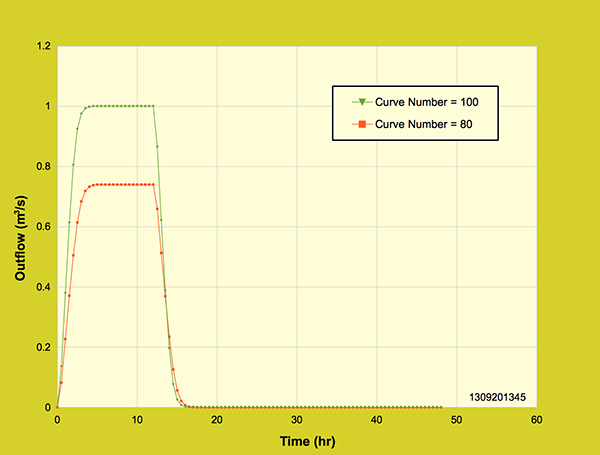
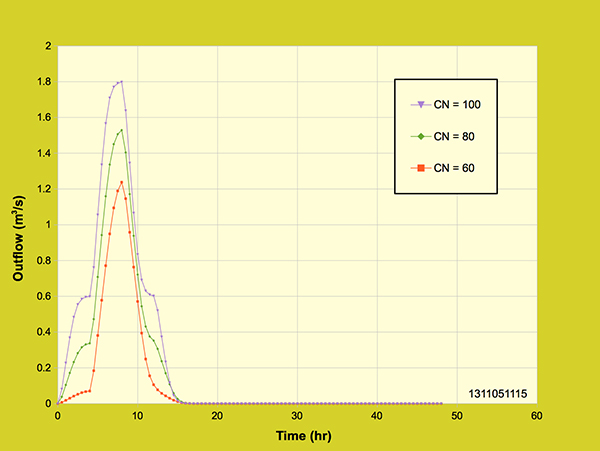
Figure 4.4.9 shows the effect of curve number on the outflow hydrograph. The curve numbers used for this run were 100 and 80. The rainfall depth (24 cm) and effective rainfall duration (12-hr) were kept constant. The outflow hydrograph for curve number 100 reached a peak outflow of 1 m3/s corresponding to a volume of 43,200 m3. For curve number 80 the outflow hydrograph reached a peak outflow of 0.74 m3/s corresponding to a volume of 31,979.891 m3. The results show that the ratio of the peak outflows (1 m3/s and 0.74 m3/s) is 0.74. Moreover, this relationship is also true for the total volumes (43,200 m3 and 31,979.891 m3) corresponding to the two peak outflows.
Figure 4.4.9. Diffusion wave model: Effect of runoff curve number on the outflow hydrograph,
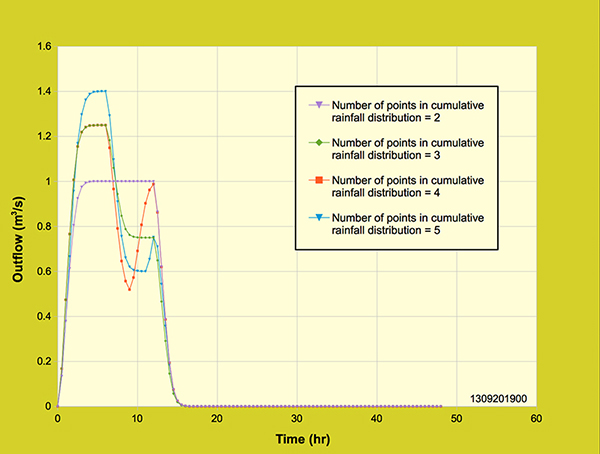
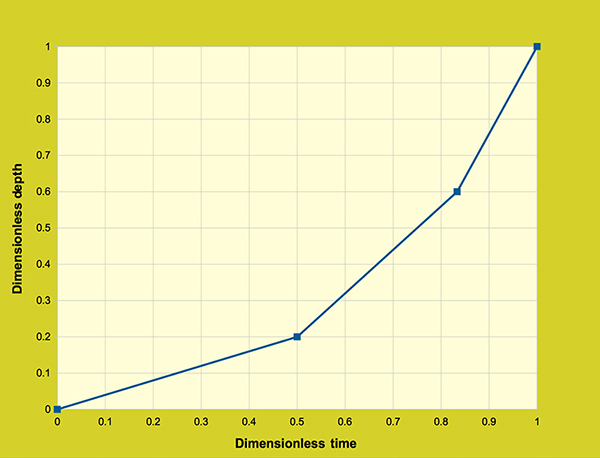
The model was also tested on the effect of cumulative rainfall distribution on the outflow hydrograph. The cumulative rainfall was distributed over 2, 3, 4 and 5 points. The average rainfall intensity (2 cm/hr) remained constant by keeping the rainfall depth (24 cm) and rainfall duration (12-hr) constant. The dimensionless cumulative time (T*) and dimensionless cumulative depth (D*) distribution are shown in Table 4.4.1 for 2, 3, 4, and 5 points.
Figure 4.4.10 shows the effect of cumulative rainfall distribution on the outflow hydrograph.
Figure 4.4.10. Diffusion wave model: Effect of shape of cumulative rainfall distribution
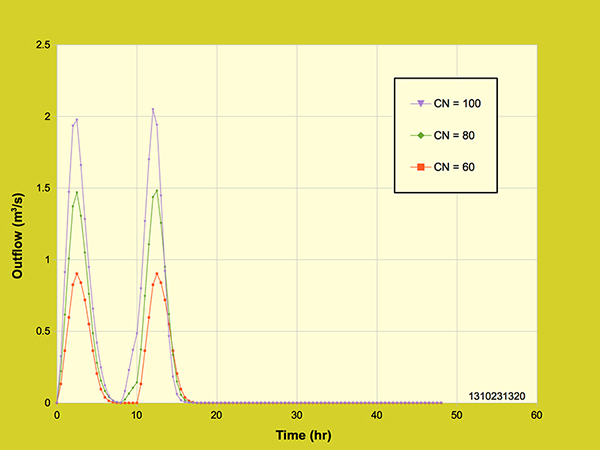
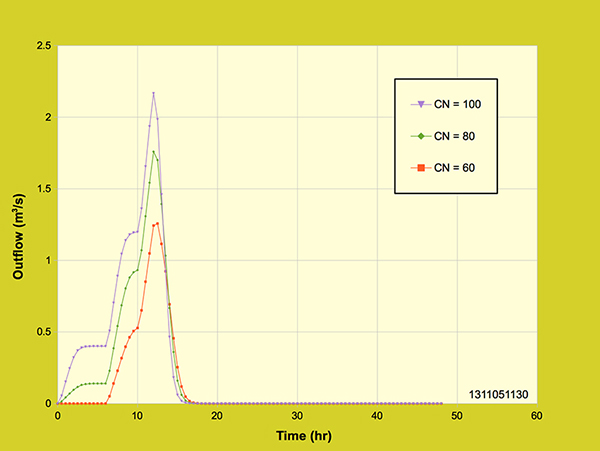
The outflow hydrograph for the 2 point distribution reached a maximum peak outflow of 1 m3/s. For the 3 point distribution, the outflow hydrograph reached a maximum peak outflow of 1.25 m3/s with an initial rainfall intensity of 2.5 cm/hr and then reducing to the second peak of 0.75 m3/s with a rainfall intensity of 1.5 cm/hr. Likewise, the outflow hydrographs for the 4 and 5 point rainfall distribution behave similarly, having more than one peak representative of the rainfall intensity distribution. As expected, the four hydrographs conserved volume (43,200 m3) regardless of the local rainfall intensity. The effect of rainfall distribution and curve number was tested by running the model for three different rainfall intensity distributions and three curve numbers. The rainfall distributions used are shown in Tables 4.4.2, 4.4.3 and 4.4.4 and the curve numbers used for the runs were 100, 80 and 60. Table 4.4.2 and Figure 4.4.11 shows the dimensionless cumulative rainfall distribution for test number 1. The rainfall intensity started at 4.8 cm/hr for the first two hours, followed by a decrease to 1.2 cm/hr for two hours, then it ceases for the next four hours, and again the rainfall intensity increases to 1.2 cm/hr and 4.8 cm/hr at two hour intervals.
Figure 4.4.11. Diffusion wave model: Dimensionless rainfall distribution - test 1.
The total hyetograph is shown in Figure 4.4.12, followed by the outflow hydrographs for the three curve numbers tested (100, 80 and 60) in Figure 4.4.13.
Figure 4.4.12. Diffusion wave model: Total hyetograph - test 1.
Figure 4.4.13. Diffusion wave model: Effect of rainfall distribution and curve number - test 1.
As shown in Figure 4.4.13, this rainfall distribution created two peaks in the outflow hydrograph and, as expected, the volume for curve number 100 is 43,200 m3, for curve number 80 is 31,979.891 m3 and for curve number 60 is 20,370.307 m3. Table 4.4.3 and Figure 4.4.14 shows the dimensionless cumulative rainfall distribution for test number 2.
Figure 4.4.14. Diffusion wave model: Dimensionless rainfall distribution - test 2.
The rainfall intensity for the first four hours was 1.2 cm/hr, followed by an increase to 3.6 cm/hr for four hours, and again the rainfall intensity decreases to 1.2 cm/hr for the last four hours. The total hyetograph is shown in Figure 4.4.15, followed by the outflow hydrographs for the three curve numbers tested (100, 80 and 60) in Figure 4.4.16.
Figure 4.4.15. Diffusion wave model: Total hyetograph - test 2.
Figure 4.4.16. Diffusion wave model: Effect of rainfall distribution and curve number - test 2.
The volume for the outflow hydrographs remain the same as in test number 1. Table 4.4.4 and Figure 4.4.17 is the corresponding the dimensionless cumulative rainfall distribution for test number 3.
Figure 4.4.17 Diffusion wave model: Dimensionless rainfall distribution - test 3.
The rainfall intensity for the first six hours was 0.8 cm/hr, followed by an increase to 2.4 cm/hr for four hours, and an increase to 4.8 cm/hr for the last two hours. The total hyetograph is shown in Figure 4.4.18, followed by the outflow hydrographs for the three curve numbers tested (100, 80 and 60) in Figure 4.4.19.
Figure 4.4.18. Diffusion wave model: Total hyetograph - test 3.
Figure 4.4.19. Diffusion wave model: Effect of rainfall distribution and curve number - test 3.
The volume for the outflow hydrographs remained the same for all three tests regardless of how the rainfall intensity was distributed. 4.5 Conclusions The preceding model results show that the diffusion wave overland flow model is numerically stable, consistent, accurate, and properly responsive to variations in rainfall distribution and hydrologic abstractions, as represented by the NRCS runoff curve number. The calculated outflow hydrographs depict the hyetograph variability and the hydrologic abstractions in an accurate and predictable manner.
5. MODEL APPLICATION
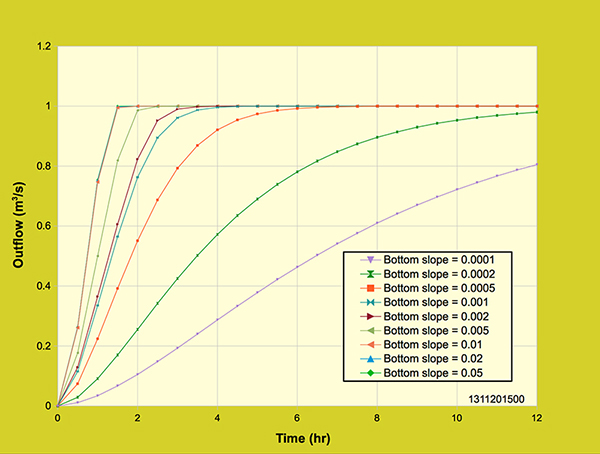
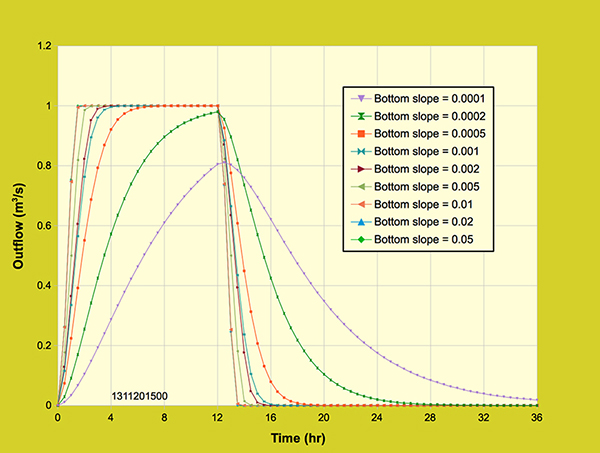
5.1 Effect of Bottom Slope The catchment response to bedslope is examined by varying the bed slope on the planes and the channel simultaneously. The bed slope on the planes and the channel was varied by running the model with nine (9) different slopes from mild to steep: (1) 0.0001 (2) 0.0002 (3) 0.0005 (4) 0.001 (5) 0.002 (6) 0.005 (7) 0.01 (8) 0.02 (9) 0.05. Figures 5.1.1, 5.1.2 and 5.1.3 show the outflow hydrographs for the nine (9) slopes tested. Figure 5.1.1 shows the detailed rising of the outflow hydrograph for the first 12-hr period.
Figure 5.1.1. Diffusion wave model: Effect of bottom slope on the outflow hydrograph.
Figure 5.1.2 is a 24-hr plot showing the peaks reached by all the hydrographs.
Figure 5.1.2. Diffusion wave model: Effect of bottom slope on the outflow hydrograph.
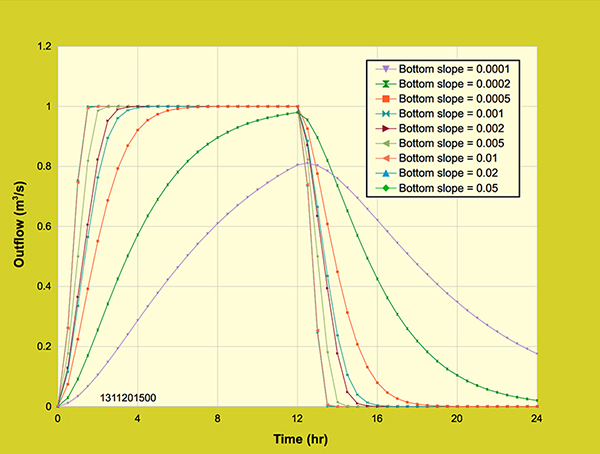
Figure 5.1.3 shows the complete outflow hydrographs, including the receding limbs.
Figure 5.1.3 Diffusion wave model: Effect of bottom slope on the outflow hydrograph.
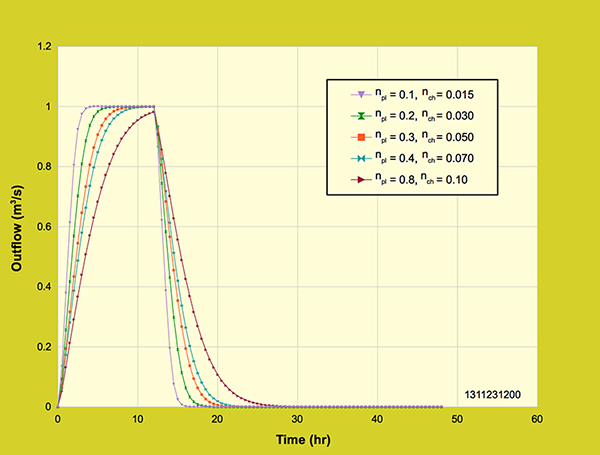
The outflow hydrograph rises in an asymptotic behavior as the slopes increase. For the very mild slopes (0.0005 and 0.002), the outflow hydrographs did not attain equilibrium outflow (1 m3/s), because of the slow rise of the hydrograph and the longer time of concentration. On the other side of the spectrum, the very steep slopes (0.01, 0.02, and 0.05) attained equilibrium outflow with a fast rise of the hydrograph and a shorter time of concentration, representing the asymptotic behavior of the kinematic wave. 5.2 Effect of Manning's n The outflow hydrograph response to the effect of Manning's n on the planes and the channel is examined. Five Manning's n for the planes and the channel were used to observe the response of the outflow hydrograph: (1) npl = 0.1, nch = 0.015, (2) npl = 0.2, nch = 0.030, (3) npl = 0.3, nch = 0.050, (4) npl = 0.4, nch = 0.070, and (5) npl = 0.8, nch = 0.10. Figure 5.2.1 shows five outflow hydrographs corresponding to the Manning's n values selected.
Figure 5.2.1. Diffusion wave model: Effect of Manning coefficient n on the outflow hydrograph.
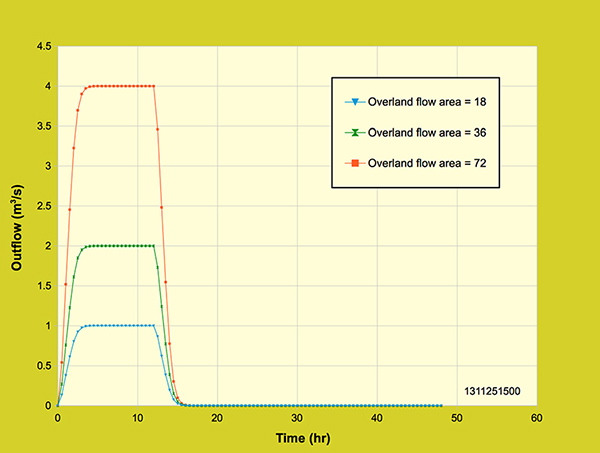
For low Manning's n values, the outflow hydrographs have a faster rising limb, attaining equilibrium outflow (1 m3/s) with a shorter time of concentration. On the other hand, for high Manning's n values, the outflow hydrographs have a longer time of concentration and attain equilibrium outflow at a later time. Moreover, for very high Manning coefficients in the plane and the channel, the outflow hydrograph did not attain equilibrium outflow. As expected, all five outflow hydrographs show the effect of Manning's n, such that the hydrograph response is delayed with an increase in Manning's n. 5.3 Effect of overland flow area and channel length Figure 5.3.1 shows three outflow hydrographs for three different overland flow areas and a constant rainfall intensity (2 cm/hr). The overland flow areas used were 18-ha, 36-ha, and 72-ha. The plane width was kept constant while the length of the channel was increased relative to the area (400 m, 800 m, and 1600 m).
Figure 5.3.1. Diffusion wave model: Effect of overland flow area and channel length
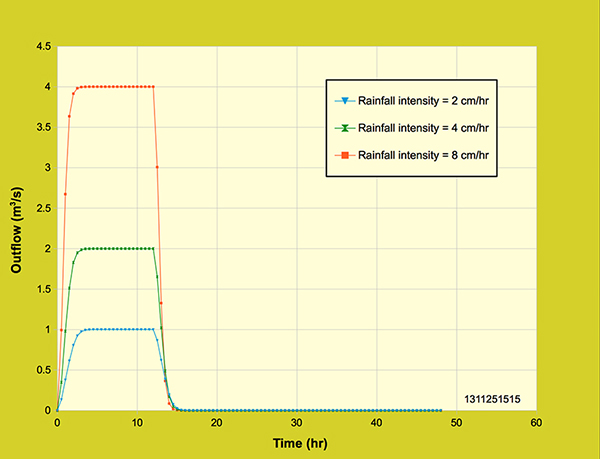
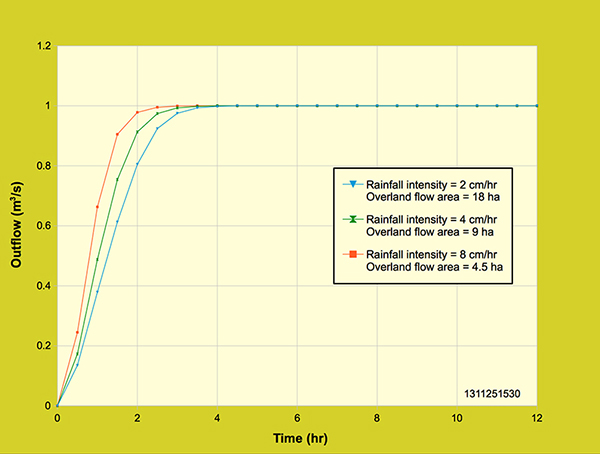
From Figure 5.3.1 it can be seen that the outflow hydrographs attained equilibrium outflow after 5 hours for the two larger areas (36-ha and 72-ha), while the overland flow through the 18-ha area reached equilibrium conditions 30 minutes before, at 4.5 hours. The 18-ha area attained an outflow of 1 m3/s; the 36-ha area attained an outflow twice as that of the 18-ha area (2 m3/s); and the 72-ha area attained an outflow twice as that of the 32 ha area (4 m3/s). Moreover, the outflow volume increased relative to the areas, which can also be observed through the outflow hydrographs. As expected, the outflow hydrographs describe well the response to an increase of overland flow area. 5.4 Effect of rainfall intensity The outflow hydrograph response to rainfall intensity is tested by varying the rainfall intensity while keeping all variables constant. The rainfall intensities used were 2 cm/hr, 4 cm/hr and 8 cm/hr. Figure 5.4.1 shows the response outflow hydrographs for the three different rainfall intensities tested on a constant overland flow area (18-ha).
Figure 5.4.1. Diffusion wave model: Effect of rainfall intensity on the outflow hydrograph.
All three outflow hydrographs attained equilibrium conditions: 1 m3/s for the 2 cm/hr rainfall intensity, 2 m3/s for the 4 cm/hr rainfall intensity and 4 m3/s for the 8 cm/hr rainfall intensity. The outflow hydrograph response for all three intensities is very similar to the outflow hydrographs generated by varying the overland flow area (Figure 5.3.1). Equilibrium conditions were attained at about the same time: 4.5 hours for the two lower intensities (2 cm/hr and 4 cm/hr), while the 8 cm/hr intensity produced an outflow hydrograph which reached equilibrium conditions 30 minutes after, at 5 hours. The outflow volumes also increase as the rainfall intensity increases over the 18-ha overland flow area. The outflow hydrograph response to varying the rainfall intensity accurately shows what is expected. 5.5 Effect of rainfall intensity and overland flow area The rainfall intensity and overland flow areas are varied to examine the response of the outflow hydrographs. The rainfall intensities and overland flow areas used were 2 cm/hr and 18-ha, 4 cm/hr and 9-ha, 8 cm/hr and 4.5-ha. Figure 5.5.1 shows a plot of the rising outflow hydrographs (12-hr) for the series of three rainfall intensities and overland flow areas tested.
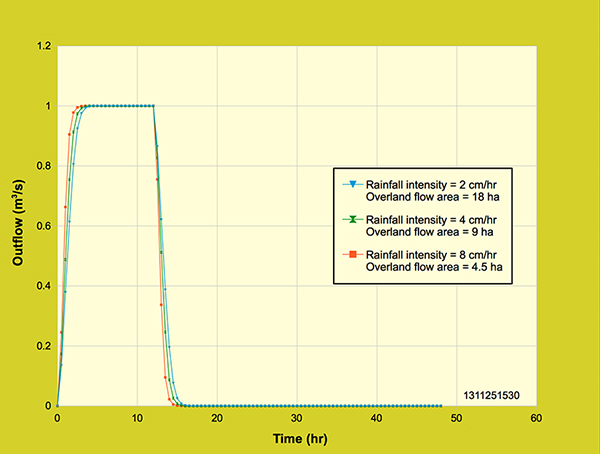
Figure 5.5.1. Diffusion wave model: Effect of overland flow area/ channel length and
Figure 5.5.2 shows the complete outflow hydrographs, including the receding limb.
Figure 5.5.2. Diffusion wave model: Effect of overland flow area/ channel length and
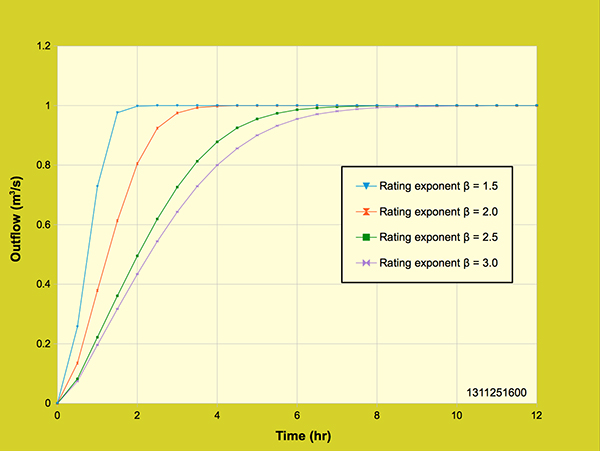
It can be seen that the outflow hydrographs for all three rainfall intensities and overland flow areas attained equilibrium outflow of 1 m3/s, while conserving the outflow volume of 43,200 m3. The peak of the outflow hydrograph was kept constant by reducing the overland flow area while increasing the rainfall intensity, to keep their product the same. Moreover, the outflow hydrograph for the 8 cm/hr rainfall intensity had a faster response than that of the 4 cm/hr. Likewise, the 4 cm/hr rainfall intensity outflow hydrograph had a faster response than that of the 2 cm/hr rainfall intensity outflow hydrograph. 5.6 Effect of rating exponent β The outflow hydrograph response to the rating exponent, β, is shown in detail in Figure 5.6.1 for the first 12 hours. Four different values for β were used to obtain the outflow hydrograph response shown in Figure 5.6.1: β = 1.5 for turbulent flow, β = 2.0 and β = 2.5 for mixed laminar-turbulent flow and β = 3.0 for laminar flow.
Figure 5.6.1. Diffusion wave model: Effect of rating exponent β
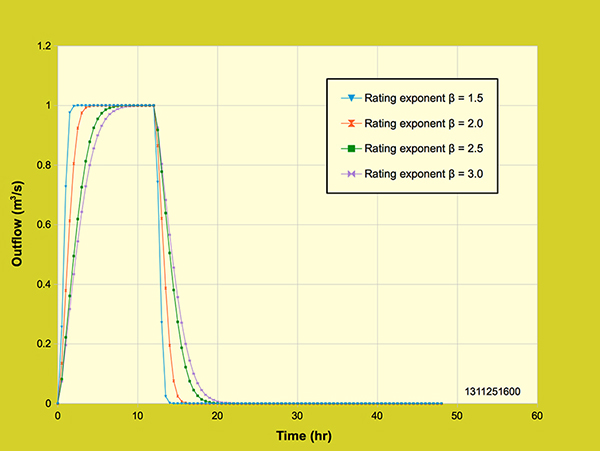
Figure 5.6.2 shows the complete outflow hydrographs, including the receding limb.
Figure 5.6.2. Diffusion wave model: Effect of rating exponent β
All four outflow hydrographs attained maximum peak outflow of 1 m3/s while conserving the outflow volume of 43,200 m3. It can be observed that for laminar conditions (β = 3) the outflow hydrograph response was slower, attaining maximum peak outflow at 11 hours, compared to that of turbulent flow (β = 1.5) which achieved the maximum peak outflow much faster at 2.5 hours. Likewise, for the mixed laminar-turbulent flows (β = 2.0 and β = 2.5), the outflow hydrograph response was in between those of laminar flow (β = 3.0) and turbulent flow (β = 1.5). 5.7 Conclusions The model applications examined here confirm the overall soundness of the diffusion wave overland flow model. The calculated outflow hydrographs clearly depict the expected results, obtained by running the model with typical variations in the following parameters: (1) bottom slope, (2) Manning's coefficient n, (3) overland flow area, (4) rainfall intensity, (5) rainfall intensity and overland flow area, keeping their product constant, and (6) rating exponent β. Its is shown that the model is responsive to the parametric variation and predictable in the results obtained.
6. ANALYSIS
6.1 Time of Concentration ONLINE OVERLAND was tested by varying the physical parameters described in Section 5. The results show that a slower rising hydrograph and, therefore, a longer time of concentration is calculated for the following cases:
6.2 Model Sensitivity to Physical Parameters ONLINE OVERLAND was tested on its sensitivity to physical parameters, as shown in Section 5. The following physical parameters were selected for testing the model: (1) bottom slope, (2) Manning's coefficient n, (3) overland flow area, (4) rainfall intensity, (5) rainfall intensity and overland flow area, and (6) rating exponent β. The bottom slope for the plane and the channel was tested by varying the slopes from mild to steep. The results clearly show the effect of the bottom slope on the outflow hydrograph. For very mild slopes, the outflow hydrographs rise very slowly, such that they do not attain equilibrium outflow. In contrast, for very steep slopes, the outflow hydrographs attained equilibrium outflow with a fast rise of the hydrograph, representing the asymptotic behavior of the kinematic wave. The effect of Manning's n was tested on the planes and the channel by varying the values from low to high. The outflow hydrographs for low values of Manning's n show a faster rising limb, attaining equilibrium outflow. In contrast, for larger values of Manning's n, the hydrograph response is delayed, thus, not attaining equilibrium outflow. The model was tested for variations of the overland flow area and channel length. The channel length increased as the overland flow area increased, keeping the width constant. The outflow hydrographs showed that the smaller area reached equilibrium conditions faster than the larger areas. As expected, the total outflow volume increased in proportion to the area. The results of this test assures the accuracy of the diffusion wave model. The sensitivity of rainfall intensity was tested by increasing the value while keeping all other variables constant. The results obtained were very similar to that of the overland flow area. The total outflow volume increased in proportion of the rainfall intensity. Accuracy of the diffusion wave model is verified by the consistency of the results. Furthermore, the rainfall intensity and overland flow area was tested to determine the response of the outflow hydrograph. The results show that volume is conserved and that equilibrium conditions are attained faster for larger rainfall intensities. Lastly, the model was tested on the rating exponent β for different flow regimes: turbulent, mixed laminar-turbulent, and laminar flow. The outflow hydrographs showed that the model conserved volume for all three flow regimes. Moreover, the outflow hydrograph for the laminar flow attained equilibrium flow at a slower rate than that of the turbulent or mixed turbulent-laminar. The results show the consistency and accuracy of the diffusion wave model.
7. SUMMARY AND CONCLUSIONS
7.1 Summary The program ONLINE OVERLAND was developed using the scripting language PHP embedded into HTML. ONLINE OVERLAND uses a simplified spatial representation of a catchment in which two rectangular planes are adjacent to a channel in the form of an open-book (Wooding 1965; Ponce 1986). The model features grid independence, in which the same results are essentially calculated regardless of the selected time interval Δt (Ponce 1979a). This distinctive feature sets the diffusion wave model apart from the kinematic wave model, which is not grid independent. The spatial interval Δx for the plane and the channel is adjusted according to the input number of time intervals NΔt, thus, assuring grid independence, model consistency and accuracy. This correct numerical behavior is due to the fact that the diffusion wave model matches the physical diffusivity with the numerical diffusivity (Ponce and Chaganti 1994a). Numerical and physical accuracy is achieved by setting the Courant number C = 1, enabling the model to minimize numerical dispersion (Ponce et al. 1979b). Extending the diffusion wave model to the realm of dynamic waves, assures the physical accuracy of the overland flow model through a wide range of boundary friction and cross-sectional shape specifications. The model uses the USDA NRCS curve number method for hydrologic abstractions. The effective runoff depth is a function of total rainfall depth and curve number CN, which is the abstraction parameter. The φ-index method is used to calculate the effective rainfall for nonuniform rainfall distributions. The φ-index method calculates a constant infiltration rate to be subtracted from the prevailing rainfall rate in order to obtain the effective runoff volume. ONLINE OVERLAND was tested for grid independence by varying the grid size and comparing it with the conventional kinematic wave model. The model sensitivity was tested by varying several parameters: (1) rainfall intensity, (2) rainfall duration, (3) overland flow area, (4) fraction of area on the left plane, (5) reference discharge fraction, (6) rating exponent β, (7) bottom slope, (8) curve number, and (9) cumulative rainfall distribution. Moreover, the diffusion wave overland flow model was tested for variations to physical parameters: (1) bottom slope, (2) Manning's coefficient n, (3) overland flow area, (4) rainfall intensity, (5) rainfall intensity and overland flow area, and (6) rating exponent β. For all the cases, the model proved to be grid independent, numerically stable, and accurate. 7.2 Conclusions An online diffusion wave model of catchment dynamics is developed using the Muskingum-Cunge method together with the scripting language PHP. The model is shown to be: (a) grid independent, (b) numerically stable, and (c) mass conservative. Model testing shows that the diffusion wave overland flow model is well behaved and properly responsive to normal variations of physical parameters. Accuracy of the model is attained by its grid independence and its ability to conserve volume. The total effective rainfall volume, after the hydrologic abstractions are taken into account, is the same as the outflow hydrograph volume for a given flood event. It is shown that the model is capable of calculating the same hydrograph regardless of the grid size, that is, the model is shown to be grid independent. The developed diffusion wave model will calculate the same peak flow and outflow hydrograph, regardless of the chosen grid size; thus, making the model consistent, reliable and predictable. Moreover, the addition of the dynamic components of the hydraulic diffusivity ensures that the model is able to simulate flood waves for a wide range of Froude and Vedernikov number conditions.
7.3 Recommendations ONLINE OVERLAND was developed to calculate the outflow hydrograph from an open-book configuration, consisting of two planes adjacent to a channel in the middle. It is recommended that the model be further extended to handle several planes, arranged both in series and in parallel.
REFERENCES
Achour, Mehdi, Friedhelm Betz, Antony Dovgal, Nuno Lopes, Hannes Magnusson, Georg Richter, Damien Seguy, and Jakub Vrana, 2014. "PHP Manual." Edited by Philip Olson. Last modified May 16. http://www.php.net/manual/en/
Cunge, J. A., 1969. "On the Subject of Flood Propagation Computation Method (Muskingum Method)." Journal of the Hydraulics Research 7:205-230.
Dooge, J. C., 1973. "Linear Theory of Hydrologic Systems. Lecture 9: Mathematical Simulation of Surface Flow." USDA Technical Bulletin No. 1468.
Horton, R. E., 1938. "The Interpretation and Application of Runoff Experiments with Reference to Soil Erosion." Proceedings of the Soil Science Society of America 3:340-349.
Izzard, C. F., 1944. "The Surface-Profile of Overland Flow." Transactions, American Geophysical Union 25:959-968.
Izzard, C. F., 1946. "Hydraulics of Runoff from Developed Surfaces." Highway Research Board, Proceedings 26:129-110.
Li, R. M., Simons, D. B. and M. A. Stevens, 1975. "Nonlinear Kinematic Wave Approximation for Water Routing." Water Resources Research 11:245-252.
Lighthill, M. J, and G. B. Whitham, 1955. "On Kinematic Waves I. Flood Movement in Long Rivers." Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 229:281-316.
Orlandini, S., and R. Rosso, 1996. "Diffusion Wave Modeling of Distributed Catchment Dynamics." Journal of Hydrologic Engineering 1:103-113.
Ponce, V. M., and V. Yevjevich, 1978. "Muskingum-Cunge Method with Variable Parameters." Journal of the Hydraulics Division 104:1663-1667.
Ponce, V. M., 1979a. "Simplified Muskingum Routing Equation." Journal of the Hydraulics Division 105:85-91.
Ponce, V. M., Chen, Y. H., and D.B. Simons, 1979b. "Unconditional Stability in Convection Computations." Journal of the Hydraulics Division 105:1079-1086.
Ponce, V. M., 1986. "Diffusion Wave Modeling of Catchment Dynamics." Journal of Hydraulic Engineering 112:716-727.
Ponce, V. M., 1989. Engineering Hydrology: Principles and practices. Prentice Hall, Englewood Cliffs, New Jersey.
Ponce, V. M., 1991a. "The Kinematic Wave Controversy." Journal of Hydraulic Engineering 117:511-525.
Ponce, V. M., 1991b. "New Perspective on the Vedernikov Number." Water Resources Research 27:1777-1779.
Ponce, V. M., and P. V. Chaganti, 1994a. "Variable-parameter Muskingum-Cunge method revisited." Journal of Hydrology 162:433-439.
Ponce, V. M., and P. T. Huston, 1994b. "New Perspective on the Convective-Diffusion-Dispersion Equation." Water Resources Research 30:1619-1620.
Schaake, J. C., 1965. "Synthesis of the Inlet Hydrograph." PhD diss., Johns Hopkins University.
Wooding, R. A., 1965. "A Hydraulic Model for the Catchment-Stream Problem." Journal of Hydrology 3:254-267.
Woolhiser, D. A. and J. A. Liggett, 1967. "Unsteady, One-Dimensional Flow over a Plane - the Rising Hydrograph." Water Resources Research 23:753-771.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||