COMPARACIÓN ENTRE

DIFUSIVIDADES HIDRÁULICAS CINEMÁTICAS Y DINÁMICAS

USANDO ONLINEOVERLAND


Victor M. Ponce y Andrea C. Scott


Universidad Estatal de San Diego, San Diego, California


220708

RESUMEN

Se evalúan y comparan dos formulaciones existentes para el coeficiente de difusividad hidráulica en el modelado de ondas de difusión de la dinámica de cuencas. Mientras que la difusividad hidráulica cinemática es independiente del número de Vedernikov, la difusividad hidráulica dinámica depende del número de Vedernikov. Usamos ONLINEOVERLAND, una herramienta analítica capaz de considerar los enfoques cinemático o dinámico para modelar la difusividad hidráulica.

Las pruebas del modelo, las cuales varían el área de drenaje, las pendientes de los planos, el exponente de la curva de gasto, y la pendiente del canal muestran la consistencia del modelo en la simulación de la respuesta de la cuenca bajo una variedad de condiciones de flujo. Los hidrogramas de salida calculados muestran correctamente el tipo de respuesta de la cuenca.

Se confirma que el problema de prueba de referencia representa una onda cinemática, que efectivamente tiene difusión nula. Por lo tanto, las diferencias en el hidrograma de salida entre las dos difusividades hidráulicas (cinemática y dinámica) resultan insignificantes. Para el problema general, que incluye todos los tipos de ondas, es decir, cinemáticas, difusivas y mixtas cinemático-dinámicas, se recomienda el uso de la difusividad hidráulica dinámica.

1.  INTRODUCCIÓN

En el modelado de ondas difusivas de la dinámica de cuencas, la difusividad hidráulica puede expresarse de dos maneras: (1) Cinemática; o (2) dinámica. La difusividad hidráulica cinemática se debe a Hayami (1951), quien fue pionero en el enfoque de ondas difusivas para el análisis de flujo superficial. Posteriormente se desarrolló una extensión del concepto de difusividad hidráulica al dominio de las ondas dinámicas, notablemente primero por Dooge y sus colaboradores (Dooge, 1973; Dooge et al., 1982), y luego por Ponce (1991a; 1991b).

La difusividad cinemática hidráulica es (Hayami, 1951):

              qo   
νk  =   _______
             2 So 		(1)

en la cual qo = descarga unitaria de referencia, y So = pendiente de fondo.

Dooge (1973) extendió el concepto de difusividad hidráulica al ámbito de las ondas dinámicas al incorporar la dependencia de esta difusividad en el número de Froude F, de la siguiente manera:

              qo                  F2
νd  =   _______ ( 1 - _______ )
             2 So                4 		(2)

en la cual νd  = difusividad hidráulica dinámica.

Posteriormente, Dooge et al. (1982) expresó la difusividad hidráulica dinámica en términos del exponente β de la curva de gasto, en la cual Q = α Aβ. La formulación mejorada es la siguiente:

              qo                  
νd  =   _______ [ 1 - (β - 1)2 F2 ]
             2 So                 		(3)

Finalmente, Ponce (1991a; 1991b) expresó la difusividad hidráulica dinámica en términos del número de Vedernikov:

              qo   
νd  =   _______  (1 - V 2)
             2 So 		(4)

en la cual el número de Vedernikov se define como sigue:


V = (β - 1) F
(5)

Mientras que la difusividad hidráulica cinemática (Ec. 1) es independiente de los números de Froude y/o Vedernikov, la difusividad hidráulica dinámica (Ec. 4) tiene un umbral claramente definido para V = 1, siendo positivo para V < 1, lo que lleva a la atenuación de la onda, y negativo para V > 1, lo que lleva a la amplificación.

Este artículo aclara el rol del número de Vedernikov en la dinámica de cuencas. La pregunta específica es la siguiente: ¿Qué tan importante es la difusividad hidráulica dinámica (Ec. 4) en la respuesta de la cuenca, bajo una amplia gama de condiciones de flujo? Exploramos esta cuestión utilizando ONLINEOVERLAND, una herramienta analítica capaz de considerar tanto la difusividad cinemática (Ec. 1) como la dinámica (Ec. 4) para modelar la difusividad. Las conclusiones pueden resultar de interés para los ingenieros y científicos que se dedican a la modelación de la dinámica de cuencas usando ondas de difusión.

2.  MODELADO DE FLUJO SUPERFICIAL

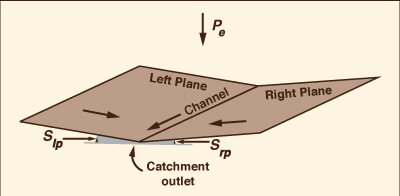
El flujo superficial es la escorrentía que fluye a través de la tierra inmediatamente después de un evento de precipitación. En la modelación de flujo superficial, la cuenca suele representarse mediante una configuración de "libro abierto", con dos planos y un canal (Wooding, 1965). La escorrentía superficial de los planos drena lateralmente hacia el canal ubicado en el centro, antes de fluir por el punto emisor de la cuenca (Fig. 1). En este artículo, usamos ONLINEOVERLAND, el cual simula la dinámica de la cuenca con el modelo de onda difusiva, utilizando una configuración de libro abierto (Ponce, 1986; Aguilar, 2014).

Fig. 1  Esquema del modelo de libro abierto ONLINEOVERLAND.

El modelo de onda difusiva representa una mejora sobre el modelo de onda cinemática convencional porque aquél es independiente de la malla. Esta propiedad refleja la capacidad del modelo para proporcionar esencialmente el mismo resultado, independientemente del tamaño de la malla. Esta importante característica, que distingue al modelo de onda difusiva de los modelos convencionales de flujo superficial, se obtiene igualando las difusividades físicas y numéricas (Cunge, 1969; Ponce, 1986). Además de las difusividades coincidentes, ONLINEOVERLAND minimiza efectivamente la dispersión numérica, es decir, el error de discretización de tercer orden, al definir la relación de malla de manera que el número de Courant, en planos y canales, sea lo más cercano posible a 1. Los retratos de amplitud y fase del modelo de onda difusiva de Muskingum-Cunge han sido documentados por Ponce y Vuppalapati (2016).

3.  PROBLEMA DE PRUEBA

Se eligió un problema de prueba de referencia para usar con ONLINEOVERLAND. Para un problema de modelación de flujo superficial dado, el programa requiere la entrada de veinticuatro (24) parámetros que describen las características geométricas y físicas del problema.

La Tabla 1 muestra los veinticuatro (24) parámetros de entrada, con los valores correspondientes adoptados en el problema de prueba. Tómese en cuenta que este último es el mismo que el conjunto de datos Entrada de muestra considerado como ejemplo en el programa. Para mayor claridad, en la Columna 3 (Valor), las siguientes filas están etiquetadas con un asterisco rojo (*):

  • Fila 11 (área de flujo A),
  • Fila 13 (pendiente del plano izquierdo Slp).
  • Fila 15 (exponente de la curva de gasto para el plano izquierdo βlp), y
  • Fila 20 (pendiente del canal Sch).

Estos parámetros se seleccionan para realizar análisis de sensibilidad. El objetivo es determinar la diferencia en la respuesta de la cuenca (es decir, el hidrograma de salida), entre los dos tipos de difusividades hidráulicas consideradas aquí: (1) Cinemática (Ec. 1); y (2) dinámica (Ec. 4). Los resultados del análisis de sensibilidad se presentan en las Secciones 4 a 7.

Tabla 1.  Datos de entrada para el problema de prueba.
(1) (2) (3)
Nº. Parámetro Valor
1 Profundidad de precipitación P 24 cm
2 Número de curva de escorrentía CN 100
3 Duración total de la precipitacióntr 12 hr
4 Número de puntos en la distribución de precipitación Np 2
5 Tiempo acumulado adimensional para la distribución de la precipitación T* 0, 1
6 Profundidad acumulada adimensional para la distribución de la precipitación D* 0, 1
7 Tiempo total de simulación Tt 48 hr
8 Número de intervalos de tiempo NΔt 96
9 Número de intervalos de tiempo para la salida Npr 1
10 Fracción utilizada para estimar el caudal de referencia Fr [Default]
11 Área de la cuenca A 18 ha *
12 Fracción del área de la cuenca en el plano izquierdo Flp 0.5
13 Pendiente del plano izquierdo Slp 0.001 *
14 Coeficiente de Manning para el plano izquierdo nlp 0.1
15 Exponente de la curva de gasto para el plano izquierdo βlp -1 *
16 Pendiente del plano derecho Srp [blank]
17 Coeficiente de Manning para el plano derecho nrp [blank]
18 Exponente de la curva de gasto para el plano derecho βrp [blank]
19 Longitud del canal Lch 400 m
20 Pendiente del canal Sch 0.01 *
21 Coeficiente de Manning del canal nch 0.015
22 Ancho de fondo del canal Bch 2 m
23 Profundidad de diseño del canal ych 0.6 m
24 Pendiente lateral del canal z [z H :1 V] 3

4.  EFECTO DEL ÁREA DE DRENAJE

En esta sección se describe la respuesta del modelo de onda difusiva a la variación del área de drenaje, es decir, el área de flujo terrestre A (Tabla 1, fila 11). Nótese que la respuesta del problema de prueba de referencia (Sección 3) es un hidrograma de flujo de captación superconcentrado, donde la duración de la precipitación (12 horas) excede el tiempo de concentración (Ponce, 2014a; 2014b). La intensidad de precipitación efectiva, correspondiente a un número de curva CN = 100 (Tabla 1, fila 2), es:

ie = P/tr = 24 cm / 12 hr = 2 cm/hr.

Por lo tanto, el flujo máximo es:

Qp = ie A = 2 cm/hr × 18 ha = 1 m3/s.

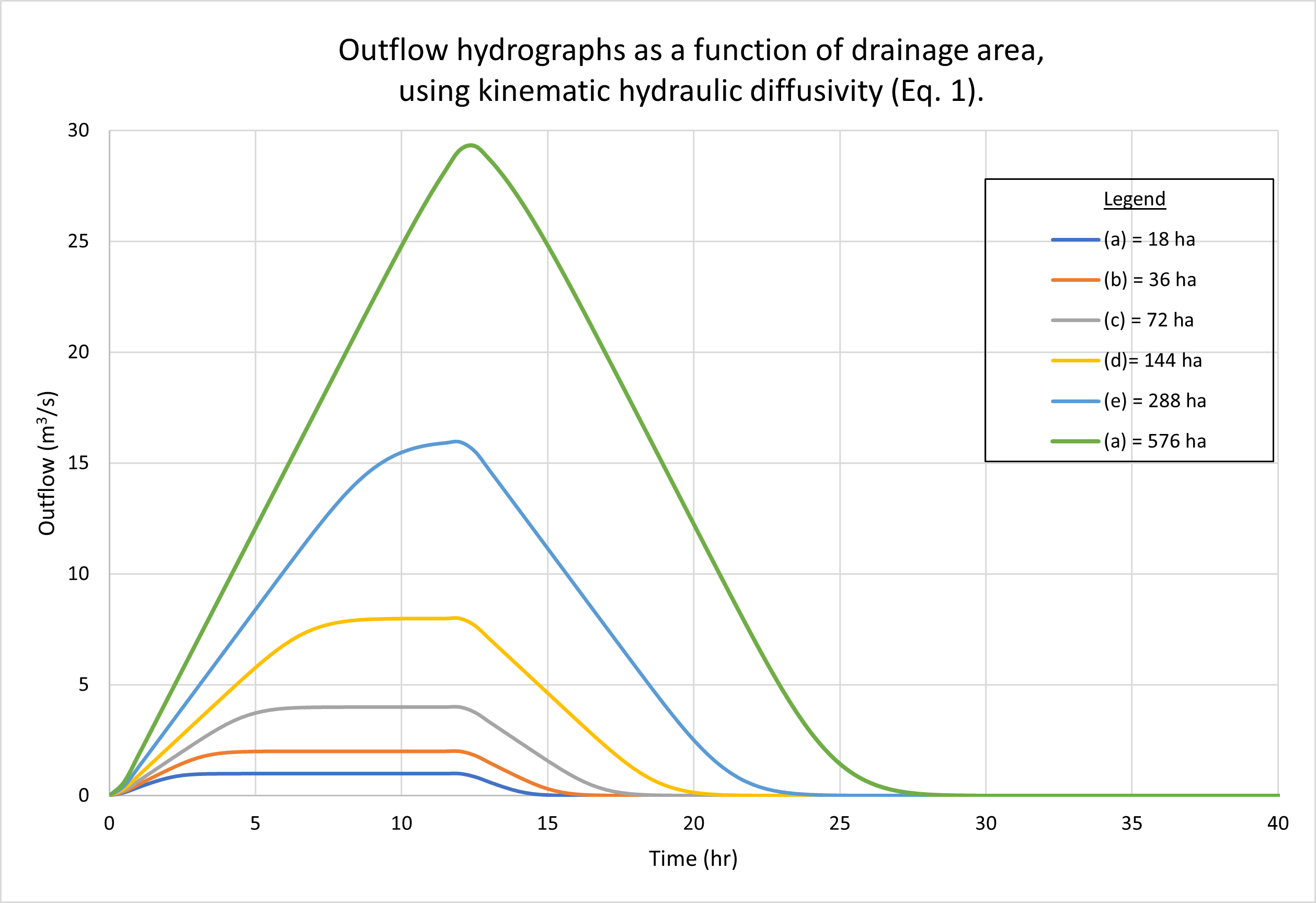
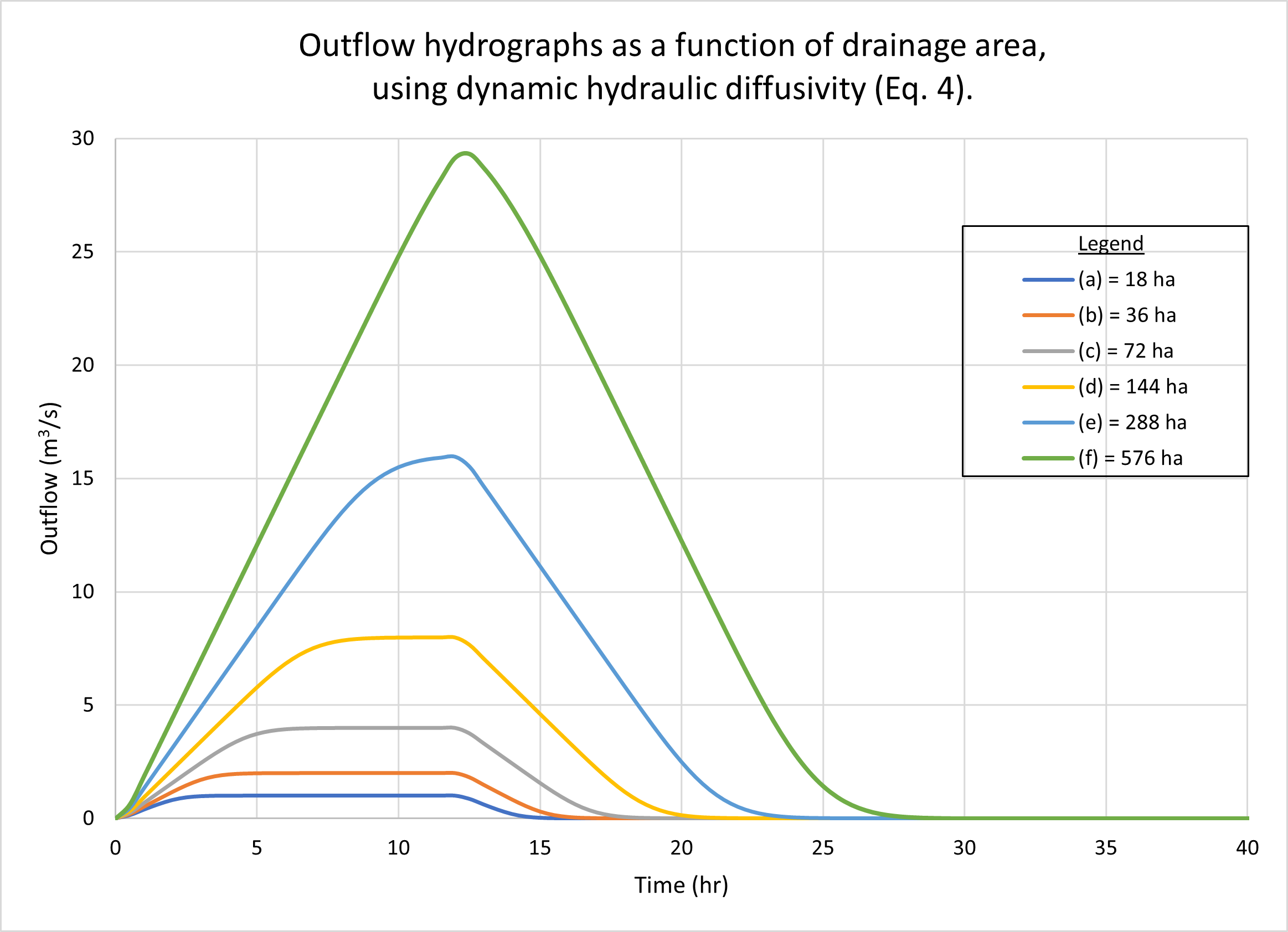
La Figura 2 muestra los hidrogramas calculados por ONLINEOVERLAND para una serie de áreas de drenaje, cada una determinada por la duplicación del valor anterior, comenzando con el problema de prueba de referencia de 18 ha, como sigue: (a) 18 ha; (b) 36 hectáreas; (c) 72 hectáreas; (d) 144 hectáreas; (e) 288 ha, y (f) 576 ha. La Figura 2 (a) muestra los resultados usando la difusividad hidráulica cinemática (Ec. 1). La Figura 2 (b) muestra los resultados utilizando la difusividad hidráulica dinámica (Ec. 4). No se puede observar una diferencia apreciable en la respuesta de la cuenca con la variación en el área de drenaje.

Observamos que mientras que los hidrogramas a, b, c y d están superconcentrados, presentando una parte superior plana típica, el hidrograma e está concentrado, con un pico distinto en el máximo posible (16 m3/s), mientras que el hidrograma f está subconcentrado, con su pico, cercano a los 29 m3/s, sin llegar a alcanzar el máximo posible de 32 m3/s.

Fig. 2 (a)  Hidrogramas de salida en función del área de drenaje,
usando difusividad hidráulica cinemática (Ec. 1).

Fig. 2 (b)  Hidrogramas de salida en función del área de drenaje,
usando difusividad hidráulica dinámica (Ec. 4).

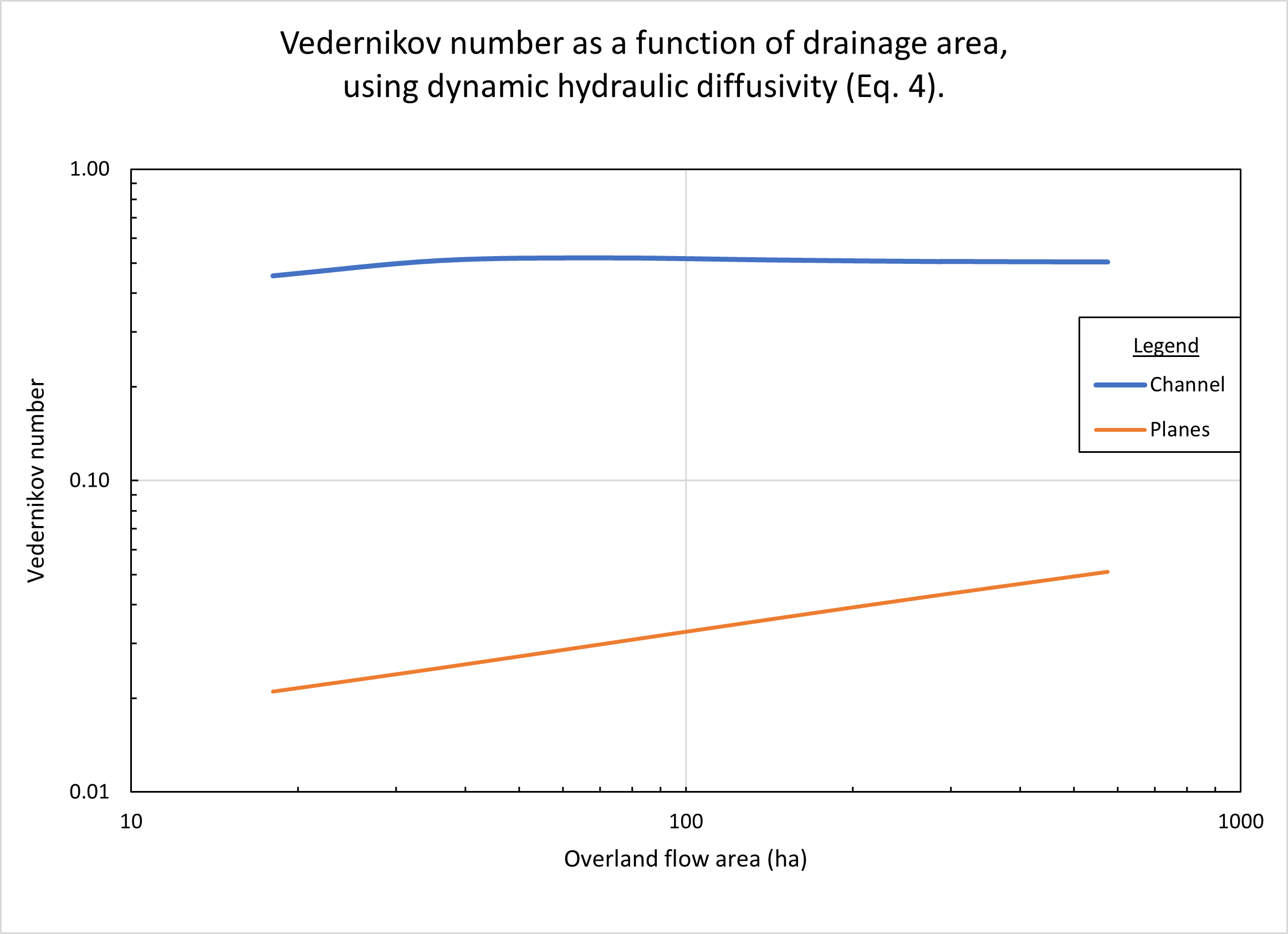
La Figura 3 muestra el número de Vedernikov calculado en función del área de drenaje, usando la difusividad hidráulica dinámica (Ec. 4). Para acomodar el flujo de salida para las áreas de drenaje más grandes, la profundidad del canal de diseño en el problema de prueba de referencia (Tabla 1, línea 23) se incrementó a 1.2 m. En los planos, los números de Vedernikov son bastante bajos, aumentando con el aumento del área de drenaje A, desde V = 0.012 para A = 18 ha , a V = 0.05 para A = 576 ha. Como era de esperar, en el canal el número de Vedernikov es relativamente alto, alrededor de V = 0.5, y permanece aproximadamente constante para todas las áreas de drenaje probadas, que varían de 18 a 576 ha.

Fig. 3  Número de Vedernikov en planos y canal, en función de la pendiente del plano.

5.  EFECTO DE LA PENDIENTE DEL PLANO

En esta sección describimos la respuesta del modelo de onda de difusión de la dinámica de la cuenca a la variación de las pendientes planas, es decir, la pendiente del plano izquierdo Slp (Tabla 1, fila 13) y la pendiente del plano derecho Srp (Tabla 1, fila 16). En todos los casos, se asume que Srp = Slp (problema de prueba de referencia).

Al igual que con la Sección 4, la respuesta del problema de prueba de referencia es un hidrograma de flujo de captación superconcentrado, en el que la duración de la precipitación (12 horas) excede el tiempo de concentración (Ponce, 2014). La intensidad de precipitación efectiva, correspondiente a un número de curva CN = 100 (Cuadro 1, fila 2), es:

ie = P/tr = 24 cm / 12 hr = 2 cm/hr.

Por lo tanto, el flujo máximo es:

Qp = ie A = 2 cm/hr × 18 ha = 1 m3/s.

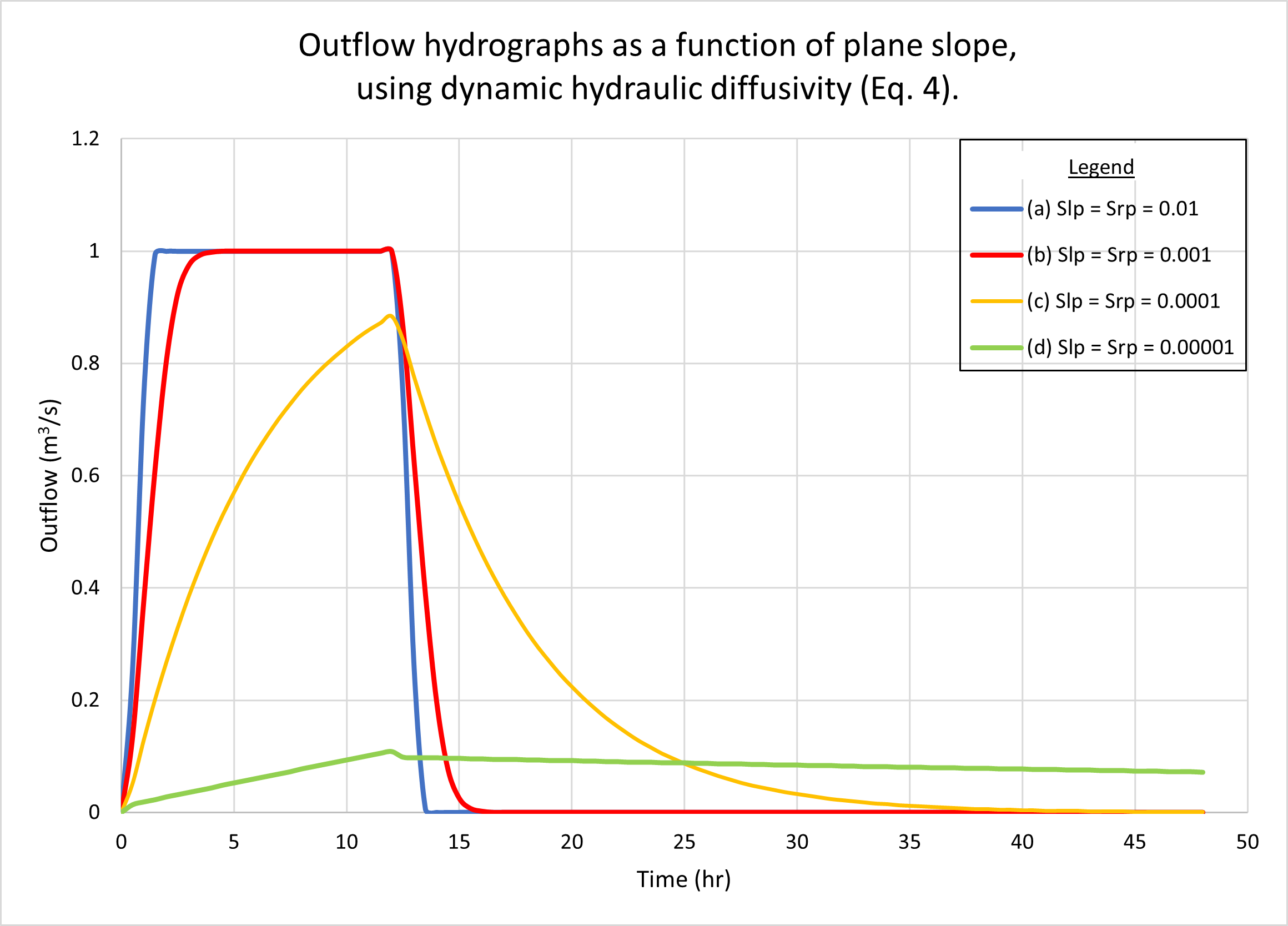
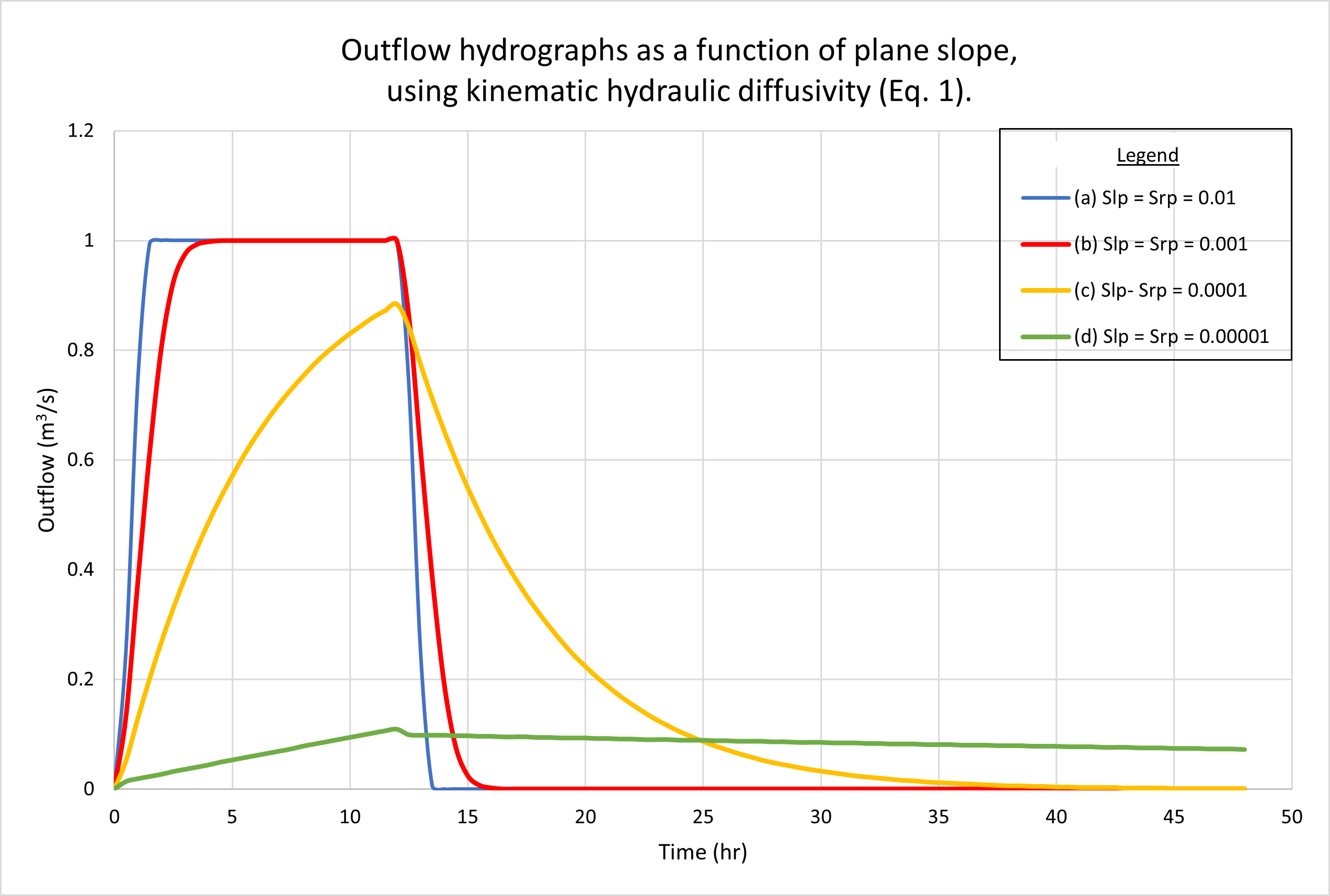
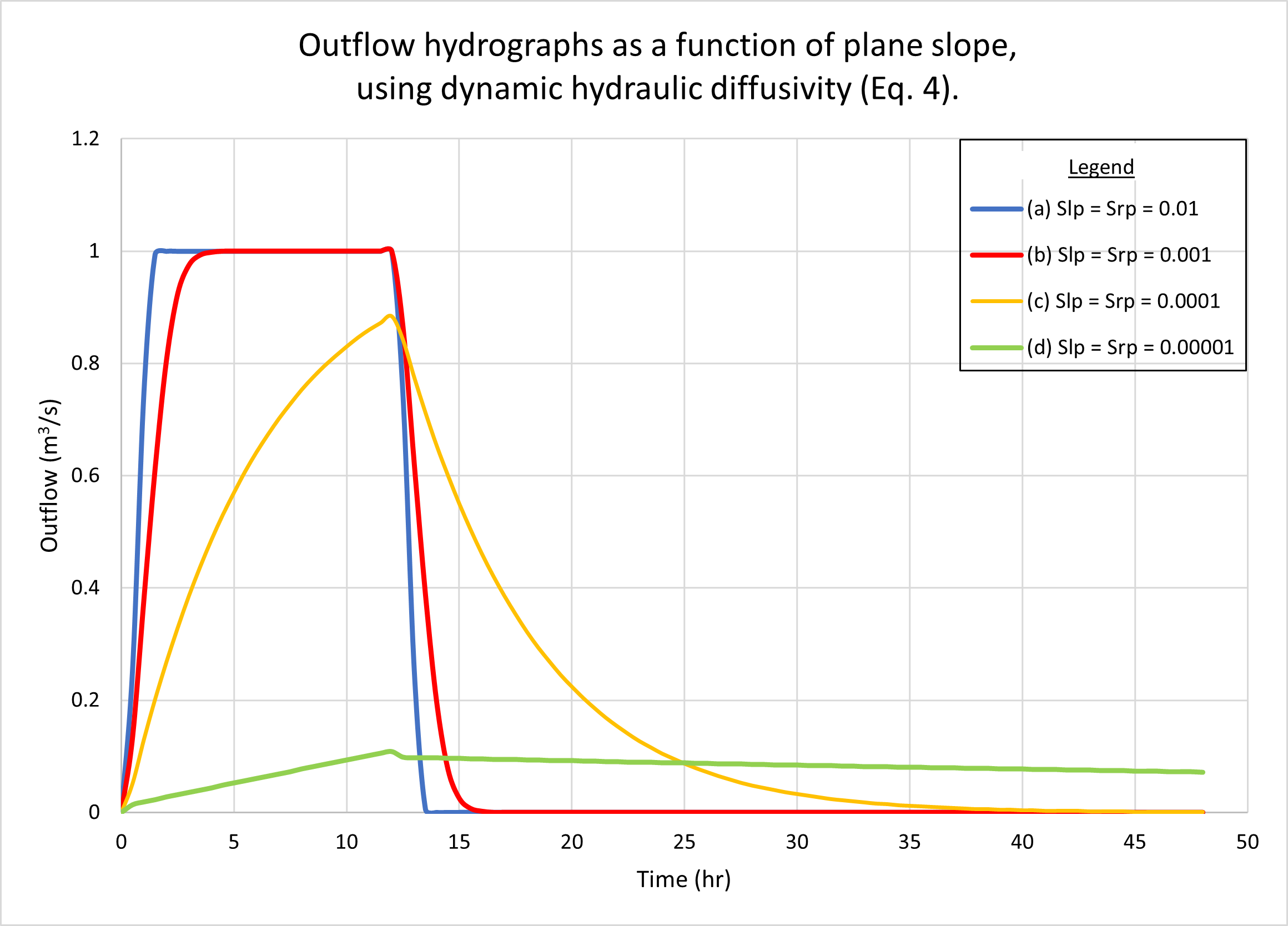
La Figura 4 muestra los hidrogramas calculados por ONLINEOVERLAND para cuatro (4) pendientes planas, como sigue: (a) 0.01; (b) 0.001; (c) 0.0001, y (d) 0.00001. La Figura 4 (a) muestra los resultados usando la difusividad hidráulica cinemática (Ec. 1). La Fig. 4 (b) muestra los resultados utilizando la difusividad hidráulica dinámica (Ec. 4). No se puede observar una diferencia apreciable en la respuesta de la cuenca entre las dos figuras.

Como era de esperarse, los hidrogramas a y b están superconcentrados, presentando la parte superior plana característica a 1 m3/s. Sin embargo, el hidrograma c está subconcentrado, con un pico definido en aproximadamente 0.88 m3/s, claramente por debajo del valor máximo posible de 1 m3 /s. El hidrograma d también está subconcentrado, con un pico de aproximadamente 0.1 m3/s. Consideramos que a medida que las pendientes del plano disminuyen, el tiempo de concentración aumenta, y finalmente supera la duración efectiva de la precipitación (12 h), lo que da como resultado un flujo de captación subconcentrado.

Fig. 4 (a)  Hidrogramas de salida en función de las pendientes planas,
utilizando la difusividad hidráulica cinemática (Ec. 1).

Fig. 4 (b)  Hidrogramas de salida en función de pendientes planas,
usando difusividad hidráulica dinámica (Ec. 4).

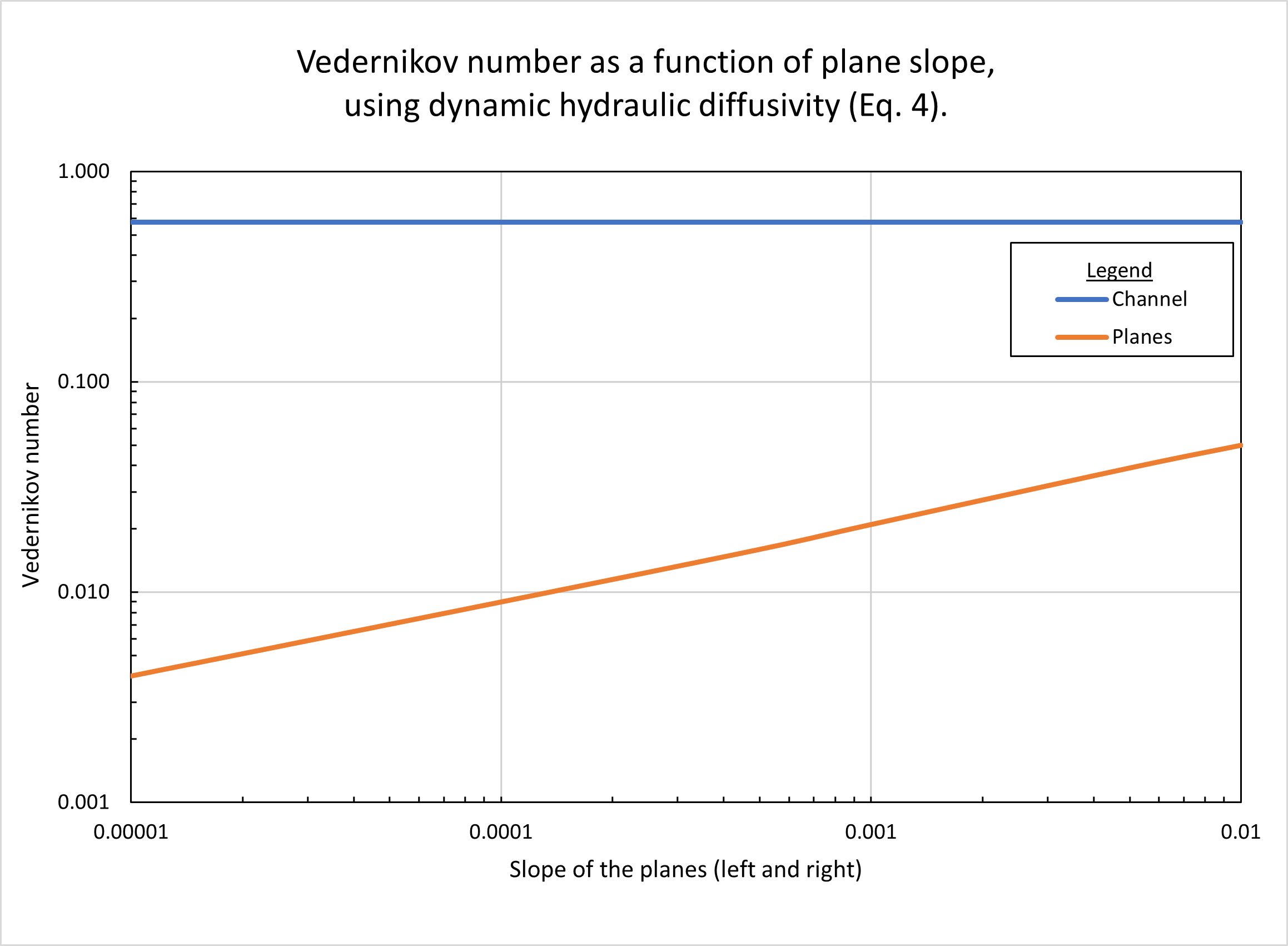
La Figura 5 muestra el número de Vedernikov calculado, en función de la pendiente del plano, usando la difusividad hidráulica dinámica (Ec. 4). En los planos, los números de Vedernikov son bastante bajos, aumentando con el aumento de la pendiente, desde V = 0.004 para una pendiente Sp = 0.00001, a V = 0.05 para una pendiente Sp = 0.01. En el canal, el número de Vedernikov es alto (V = 0.58) y permanece constante (con la variación de la pendiente del plano), ya que la pendiente relativamente alta del canal (Sch = 0.01) es constante y corresponde al problema de prueba de referencia (Tabla 1, fila 20).

Fig. 5  Vedernikov number in planes and channel, as a function of plane slope.

6.  EFECTO DEL EXPONENTE DE LA CURVA DE GASTO

En esta sección describimos la respuesta del modelo de onda difusiva de la dinámica de la cuenca a la variación en el exponente de la curva de gasto β. En el flujo de superficie libre, este último varía con el tipo de fricción y la forma de la sección transversal (Ponce, 2014c). Seleccionamos tres valores de β, los tres correspondientes a un canal hidráulicamente ancho, variando el tipo de fricción del fondo de la siguiente manera: (1) Manning turbulento, β = 5 /3; (2) mixto 50% laminar - 50% turbulento Manning, β = 7/3; y (3) laminar, β = 9/3, es decir, β = 3.

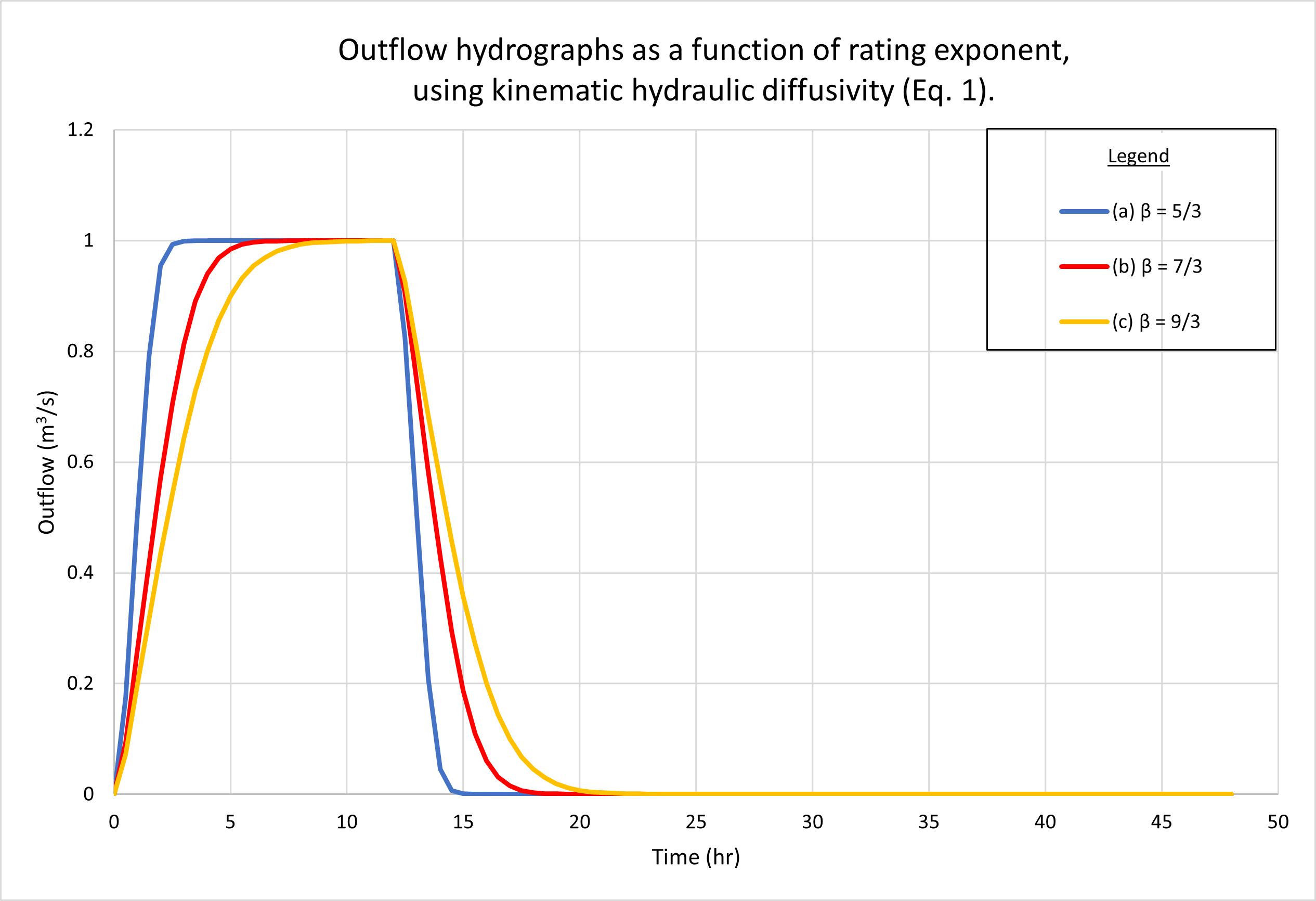
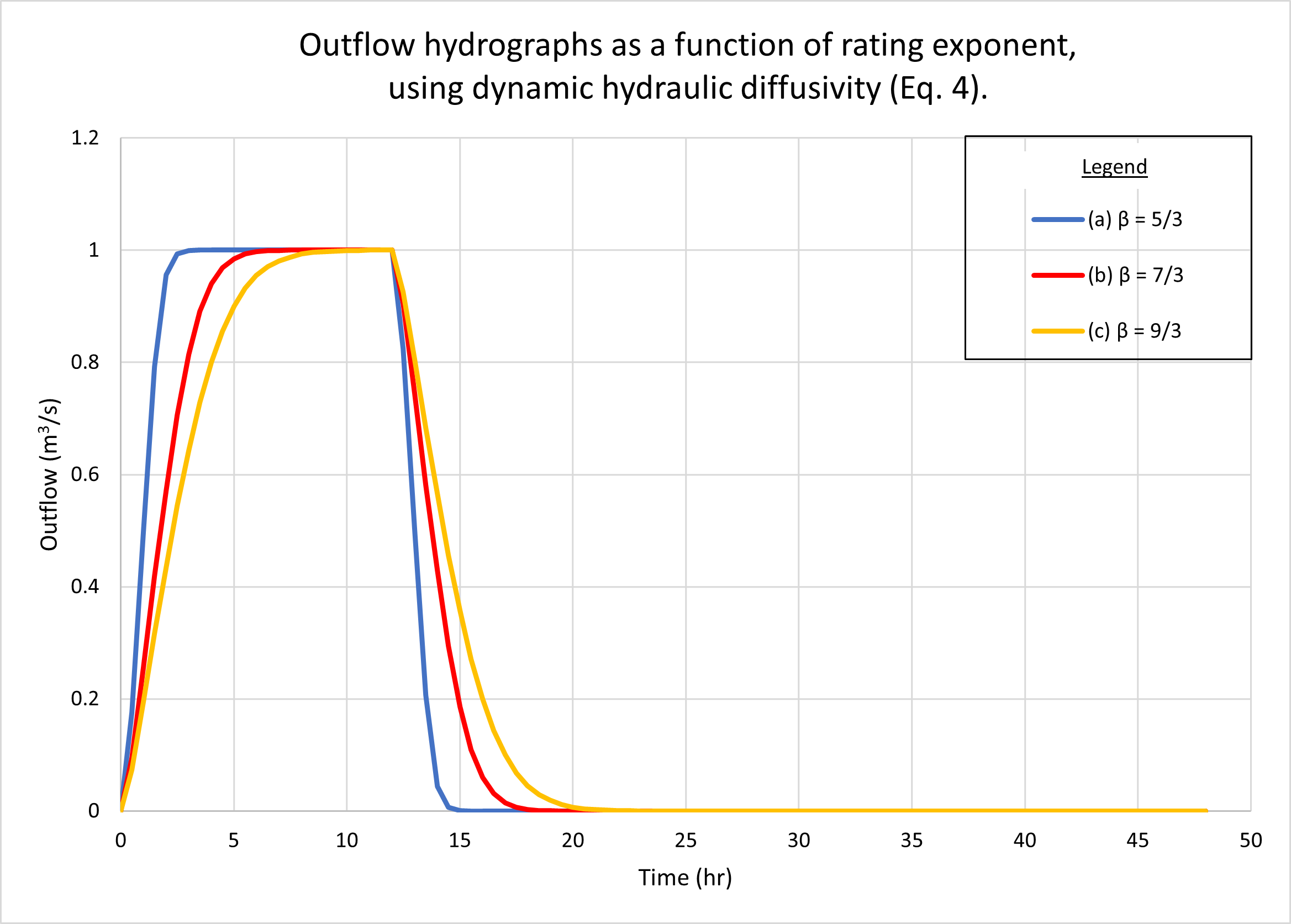
Figure 6 muestra los hidrogramas calculados por ONLINEOVERLAND. La Figura 6 (a) muestra los resultados usando la difusividad hidráulica cinemática (Ec. 1). La Fig. 6 (b) muestra los resultados utilizando la difusividad hidráulica dinámica (Ec. 4). No se puede observar una diferencia apreciable en la respuesta de la cuenca entre las dos figuras.

Tómese en cuenta que los tres hidrogramas, a, b y c, están superconcentrados, presentando la parte superior plana característica a 1 m3/s. Sin embargo, la cantidad de difusión del hidrograma (en este caso, un aumento en la base de tiempo del hidrograma) aumenta con el valor de β (de β = 5/3, Manning turbulento, a β = 9/3, laminar). Estos resultados se asemejan a los de Aguilar (2014).

Fig. 6 (a)  Hidrogramas de salida en función del exponente de la curva de gasto,
utilizando la difusividad hidráulica cinemática (Ec. 1).

Fig. 7 (b)  Hidrogramas de flujo de salida en función del exponente de la curva de gasto,
usando difusividad hidráulica dinámica (Ec. 4).

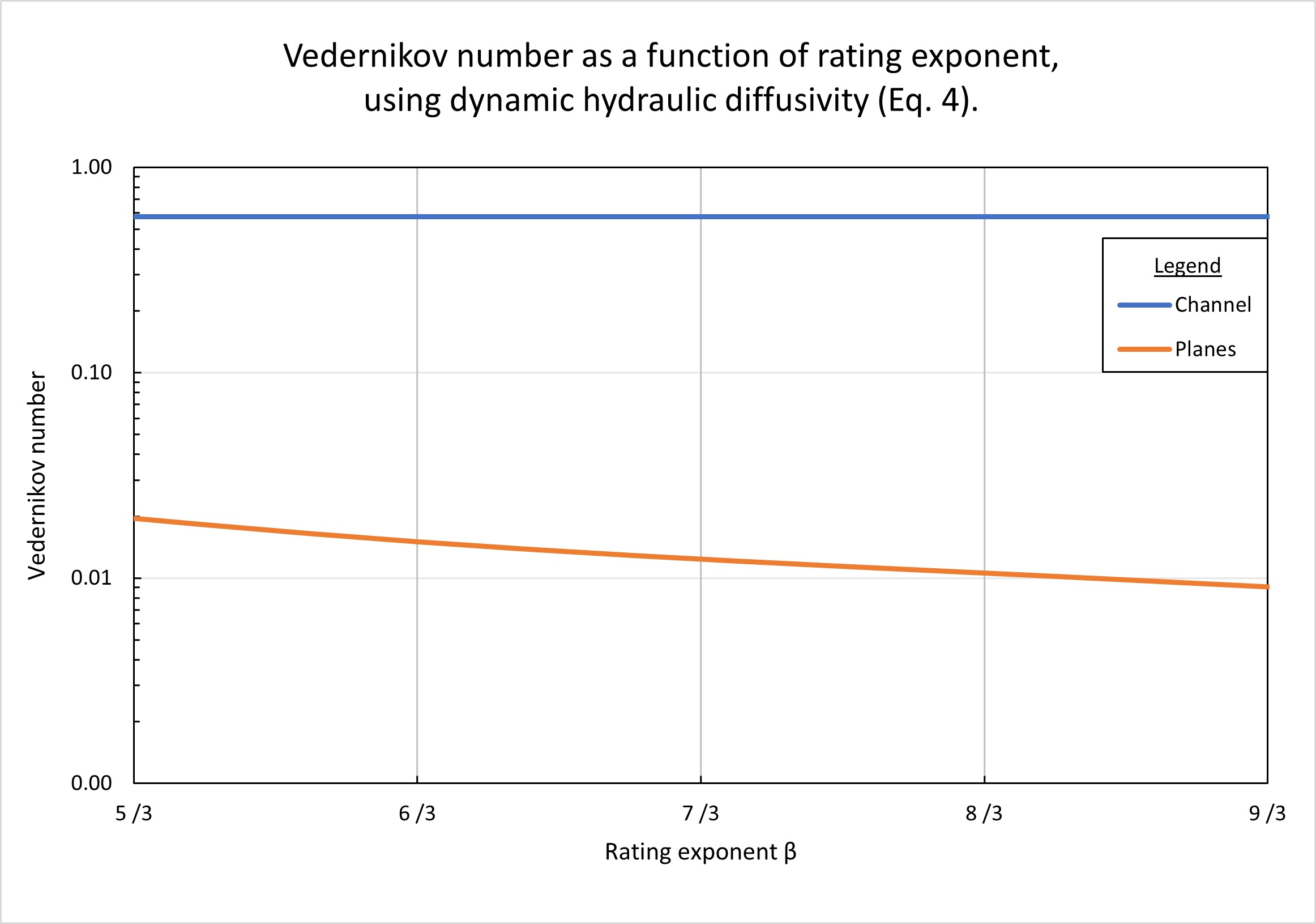
La Figura 7 muestra el número de Vedernikov calculado en función del exponente de la curva de gasto β, usando la difusividad hidráulica dinámica (Ec. 4). En los planos, los números de Vedernikov son bastante bajos, disminuyendo con un aumento en β, desde V = 0.02 para β = 5/3 (Manning turbulento), a V = 0.0085 para β = 9/3 (flujo laminar). En el canal, el número de Vedernikov es alto (V = 0.58) y permanece constante (con la variación del exponente de la curva de gasto en los planos), ya que la pendiente del canal relativamente alta (S ch = 0.01) es constante y corresponde al problema de prueba de referencia (Tabla 1, fila 20).

Fig. 7  Número de Vedernikov en función del exponente de la curva de gasto.

7.  EFECTO DE LA PENDIENTE DEL CANAL

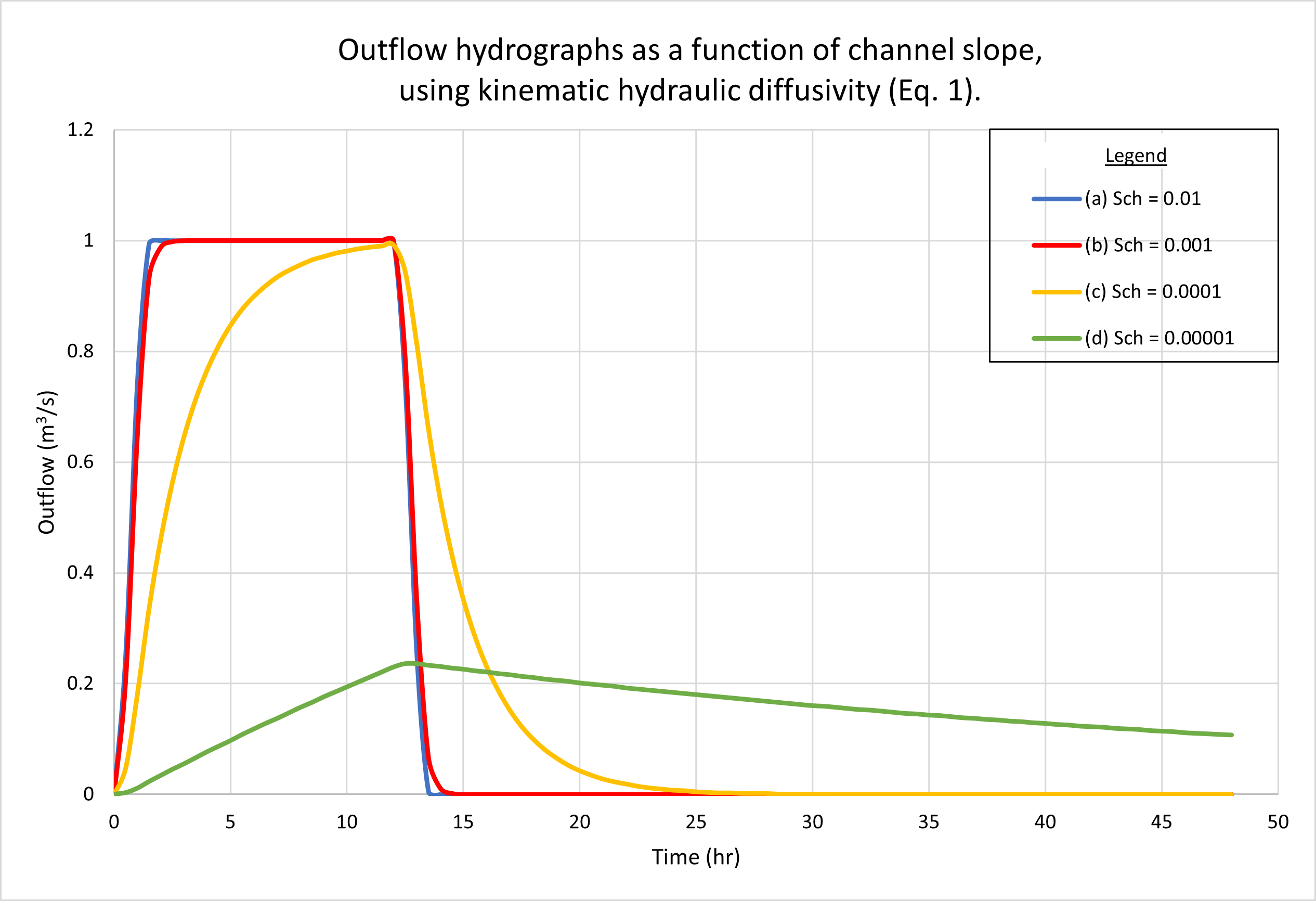
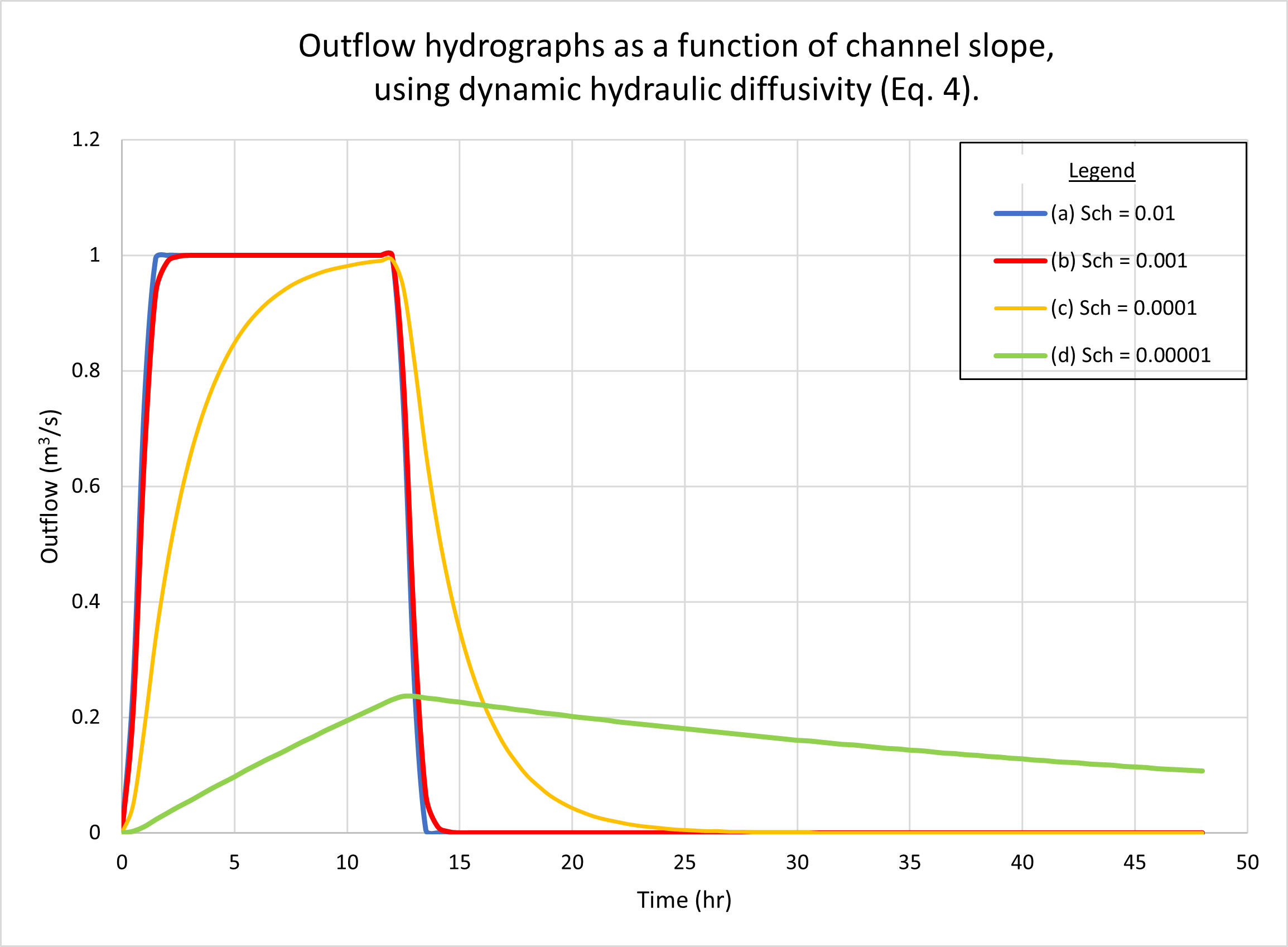
La Figura 8 muestra los hidrogramas calculados por ONLINEOVERLAND para cuatro (4) pendientes de canal, como sigue: (a) 0.01; (b) 0.001; (c) 0.0001, y (d) 0.00001. La Figura 8 (a) muestra los resultados usando la difusividad hidráulica cinemática (Ec. 1). La Fig. 8 (b) muestra los resultados utilizando la difusividad hidráulica dinámica (Ec. 4). No se puede observar una diferencia apreciable en la respuesta de la cuenca entre las dos figuras.

Como era de esperarse, los hidrogramas a y b están superconcentrados, presentando la parte superior plana característica a 1 m3/s. El hidrograma c está débilmente superconcentrado, con un pico estrecho distintivo cercano a 1 m3/s, el hidrograma d está fuertemente subconcentrado, con su pico en unos 0.24 m3/s. Consideramos que a medida que las pendientes del plano disminuyen, el tiempo de concentración aumenta, y finalmente supera la duración efectiva de la lluvia (12 h), lo que da como resultado un flujo subconcentrado.

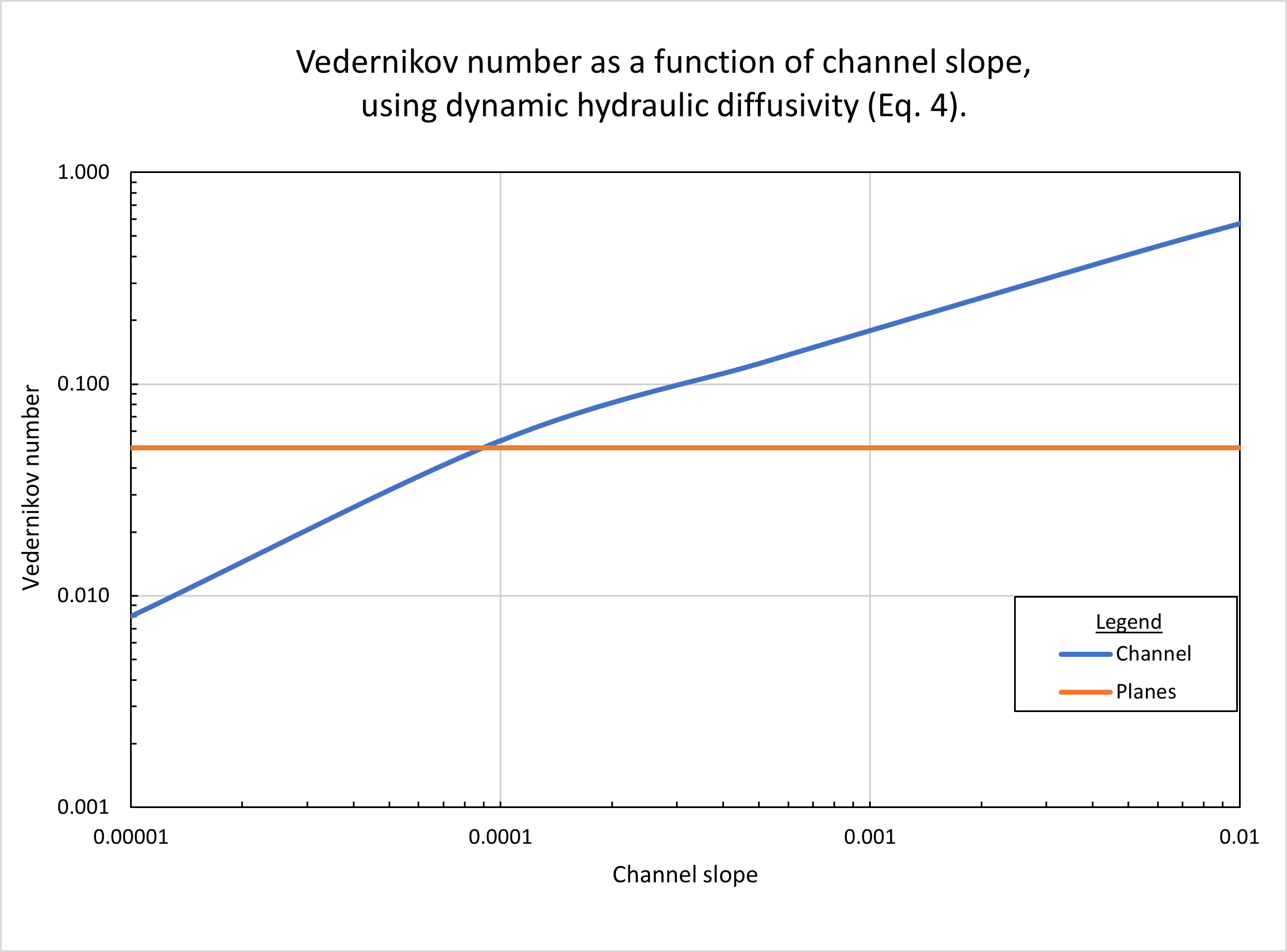
Fig. 8 (a)  Hidrogramas de salida para varias pendientes de fondo.

Fig. 8 (b)  Hidrogramas de salida para varias pendientes de fondo.

La Figura 9 muestra el número de Vedernikov calculado en función de la pendiente de fondo, utilizando la difusividad hidráulica dinámica (Ec. 4). En los planos, los números de Vedernikov se mantienen constantes e iguales a V = 0.05, ya que los pendientes del plano no han cambiado: Slp = Srp = 0.001, correspondiente al problema de prueba de referencia (Tabla 1, filas 13 y 16, respectivamente). Como era de esperarse, en el canal los números de Vedernikov aumentar con gran dureza, desde V = 0.008 para una pendiente de fondo muy suave (Sch = 0.00001), a V = 0.55 (caudal casi crítico) para una pendiente relativamente empinada (Sch = 0.01 ).

Fig. 9  Número de Vedernikov en función de la pendiente de fondo.

8.  ANÁLISIS

Los resultados de las Secciones 4 a 7 han demostrado claramente que la diferencia en los hidrogramas de salida entre las dos formulaciones para la difusividad hidráulica (cinemática, Ec. 1; y dinámica, Ec. 4) es insignificante para las condiciones de flujo probadas enumeradas en la Tabla 1. La razón de este comportamiento se debe a las características de propagación de ondas superficiales (Ponce, 2019). Las ondas cinemáticas no se difusionan; por lo tanto, para las ondas cinemáticas, cualquier diferencia en la forma en que se calcula la difusión (es decir, la Ec. 1 frente a la Ec. 4) es insignificante. Adicionalmente, para las ondas difusivas, cualquier diferencia en la forma en que se calcula la difusión sería pequeña. Para ondas cinemático-dinámicas mixtas, cualquier diferencia en la forma en que se calcula la difusión sería considerable.

La onda probada en el problema de prueba de referencia (Tabla 1) es una onda típica que se encuentra en la práctica hidrológica; por lo tanto, es muy probable que sea cinemática. Para probar esta afirmación, usamos el criterio de aplicabilidad de la onda cinemática desarrollado por Ponce et al. (1978), que viene dada por la siguiente desigualdad: T So (uo /do) ≥ 171. Para el problema de prueba de referencia, la duración del hidrograma es T = 12 h, y la pendiente del canal es So = 0.01. Los valores aplicables de velocidad media uo y profundidad de flujo do, en función de las dimensiones del canal (Tabla 1 , filas 22 y 24) son los siguientes: uo = 2 m/s, y do = 0.2 m. Esto conduce a: T So (uo /do ) = 4320 ≥ 171, lo que confirma que la onda ensayada es decididamente cinemática.

Consideramos que es más probable que las ondas de difusión y mixtas cinemático-dinámicas estén presentes en situaciones inusuales, aparentando ser la excepción y no la regla (Lighthill and Whitham, 1955). Sin embargo, reconocemos que la Ec. 4 es más completa que la Ec. 1 en la descripción de la dinámica de los fenómenos de flujo, y que resuelve correctamente, sin complejidad adicional, todos los tipos de ondas, incluidas las cinemáticas, las de difusión y las mixtas cinemático-dinámicas. Por lo tanto, la Ec. 4 debería ser la forma preferida de calcular el coeficiente de difusividad hidráulica en el modelado de cuencas.

9.  RESUMEN

Se evalúan y comparan dos formulaciones existentes para el coeficiente de difusividad hidráulica en el modelado de ondas difusivas de la dinámica de cuencas (Ecuaciones 1 y 4). Mientras que la difusividad hidráulica cinemática (Ec. 1) es independiente del número de Vedernikov, la difusividad hidráulica dinámica (Ec. 4) es dependiente. Usamos el programa ONLINEOVERLAND, una herramienta analítica capaz de considerar los enfoques cinemático (Ec. 1) o dinámico (Ec. 4) para modelar la difusividad hidráulica. El objetivo es comparar el comportamiento de estos dos enfoques en la generación de hidrogramas de salida para configuraciones de libro abierto. Para este propósito, usamos el problema de prueba de referencia descrito en la Tabla 1.

Las pruebas del modelo variando el área de drenaje A, pendientes de los planos Slp y Srp, el exponente de la curva de gasto β, y la pendiente del canal Sch, muestran la consistencia del modelo en la simulación de la respuesta de la cuenca bajo una amplia variedad de condiciones de flujo. Los hidrogramas de salida calculados muestran correctamente el tipo de respuesta de la cuenca, mostrando un flujo de cuenca superconcentrado, concentrado o subconcentrado, según los datos de entrada.

Se confirma que el problema de prueba de referencia representa una onda cinemática, con difusión nula. Por lo tanto, las diferencias en el hidrograma de salida entre las dos difusividades hidráulicas (cinemática, Ec. 1 y dinámica, Ec. 4) resultan insignificantes (Figs. 2, 4, 6 y 8). Para el problema general, que incluye todos los tipos de ondas, es decir, cinemáticas, difusivas, y mixtas cinemático-dinámicas, se recomienda el uso de la difusividad hidráulica dinámica, ya que es más precisa que su contraparte cinemática, y no aumenta la complejidad del modelo.

BIBLIOGRAFÍA

Aguilar, R. D. 2014. Diffusion wave modeling of catchment dynamics using online calculation. M.S. Thesis, Department of Civil, Construction, and Environmental Engineering, San Diego State University, San Diego, California; online version.

Cunge, J. A. 1969. On the Subject of a Flood Propagation Computation Method (Muskingum Method), Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.

Dooge, J. C. I. 1973. Linear theory of hydrologic systems. Technical Bulletin No. 1468, U.S. Department of Agriculture, Washington, D.C. Dooge (1973).

Dooge, J. C. I., W. B. Strupczewski, y J. J. Napiorkoswki. 1982. Hydrodynamic derivation of storage parameters in the Muskingum model. Journal of Hydrology, 54, 371-387.

Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December.

Lighthill, M. J., y G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.

Ponce, V. M. 1978. Applicability of kinematic and diffusion models. Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY3, 353-360.

Ponce, V. M. 1986. Diffusion wave modeling of catchment dynamics. Journal of Hydraulic Engineering, ASCE, Vol. 112, No. 8, 716-727.

Ponce, V. M. 1991a. The kinematic wave controversy. Journal of Hydraulic Engineering, ASCE, Vol. 117, No. 4, April, 511-525.

Ponce, V. M. 1991b. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.

Ponce, V. M. 2014a. Engineering Hydrology: Principles and Practices, Section 2.4: Runoff. Online textbook.

Ponce, V., M. 2014b. Runoff diffusion reexamined. Online publication.

Ponce, V. M. 2014c. Fundamentals of Open-channel Hydraulics, Section 1.2: Types of Flow. Online textbook.

Ponce, V., M, y V. Vuppalapati. 2016. Muskingum-Cunge amolitude and phase portraits with online computation. Online publication.

Ponce, V., M. 2019. The S-curve explained. Online publication.

Wooding, R. A. 1965. A hydraulic model for the catchment-stream problem. I. Kinematic wave theory. Journal of Hydrology, Vol. 3, Nos. 3/4, pp. 254-267.

221124