COMPARISON BETWEEN

KINEMATIC AND DYNAMIC HYDRAULIC DIFFUSIVITIES

USING SCRIPT ONLINEOVERLAND


Victor M. Ponce and Andrea C. Scott


San Diego State University, San Diego, California


220708

ABSTRACT

Two existing formulations for the coefficient of hydraulic diffusivity in diffusion wave modeling of catchment dynamics are evaluated and compared. While the kinematic hydraulic diffusivity is independent of the Vedernikov number, the dynamic hydraulic diffusivity is dependent on the Vedernikov number. We use the script ONLINEOVERLAND, an analytical tool capable of considering either the kinematic or dynamic approaches to model hydraulic diffusivity. For this purpose, we use the reference test problem.

Testing of the model varying the drainage area, plane slopes, rating exponent, and channel slope show the model's consistency in simulating catchment response under a variety of flow conditions. Calculated outflow hydrographs correctly show the type of catchment response, showing either superconcentrated, concentrated, or subconcentrated catchment flow, depending on the input data.

The reference test problem is confirmed to depict a kinematic wave, effectively featuring zero wave diffusion. Therefore, the differences in outflow hydrograph between the two hydraulic diffusivities (kinematic and dynamic) are shown to be negligible. For the general problem, which includes all types of shallow-water waves, i.e., kinematic, diffusion, and mixed kinematic-dynamic, the use of the dynamic hydraulic diffusivity is recommended.

1.  INTRODUCTION

In diffusion wave modeling of catchment dynamics, the hydraulic diffusivity may be expressed in two alternative ways: (1) kinematic; or (2) dynamic. The kinematic hydraulic diffusivity is due to Hayami (1951), who pioneered the diffusion wave approach to surface flow. An extension of the concept of hydraulic diffusivity to the domain of dynamic waves followed, notably first by Dooge and his collaborators (Dooge, 1973; Dooge et al., 1982), and later by Ponce (1991a; 1991b).

The kinematic hydraulic diffusivity is (Hayami, 1951):

              qo   
νk  =   _______
             2 So 		(1)

in which qo = reference unit-width discharge, and So = bottom slope.

Dooge (1973) extended the concept of hydraulic diffusivity to the realm of dynamic waves by incorporating the dependency of the hydraulic diffusivity on the Froude number F, as follows:

              qo                  F2
νd  =   _______ ( 1 - _______ )
             2 So                4 		(2)

in which νd  = dynamic hydraulic diffusivity.

Subsequenty, Dooge et al. (1982) expressed the dynamic hydraulic diffusivity in terms of the exponent β of the discharge-area rating curve, wherein Q = α A β. The enhanced formulation is the following:

              qo                  
νd  =   _______ [ 1 - (β - 1)2 F2 ]
             2 So                 		(3)

Ponce (1991a; 1991b) expressed the dynamic hydraulic diffusivity in terms of the Vedernikov number:

              qo   
νd  =   _______  (1 - V 2)
             2 So 		(4)

in which the Vedernikov number is:


V = (β - 1) F
(5)

While the kinematic hydraulic diffusivity (Eq. 1) is independent of the Froude and/or Vedernikov numbers, the dynamic hydraulic diffusivity (Eq. 4) has a clearly defined threshold for V = 1, being positive for V < 1, leading to wave attenuation, and negative for V > 1, leading to wave amplification.

This paper sheds light on the role of the Vedernikov number in catchment dynamics. The specific question to be answered is the following: How important is the dynamic hydraulic diffusivity (Eq. 4) in affecting catchment response, under a wide range of flow conditions? We explore this question by using the script ONLINEOVERLAND, an analytical tool capable of considering either the kinematic (Eq. 1) or dynamic (Eq. 4) approaches to model hydraulic diffusivity. The conclusions may prove of interest to engineers and scientists engaged in diffusion wave modeling of catchment dynamics.

2.  OVERLAND FLOW MODELING

Overland flow is surface runoff that flows across the land immediately following a rainfall event. In overland flow modeling, the catchment is typically represented by an "open-book" configuration, with two planes and one channel (Wooding, 1965). Surface runoff from the planes drains laterally into the centrally located channel before flowing out through the catchment outlet (Fig. 1). In this article, we use the script ONLINEOVERLAND, which simulates catchment dynamics with the diffusion wave model, using an open-book configuration (Ponce, 1986; Aguilar, 2014).

Fig. 1  ONLINEOVERLAND open-book model schematic.

The diffusion wave model is an improvement over the conventional kinematic wave model because it is grid independent. This property reflects the model's ability to provide essentially the same result, regardless of grid size. This significant feature, which sets the diffusion wave model apart from conventional overland flow models, is obtained by matching physical and numerical diffusivities (Cunge, 1969; Ponce, 1986). In addition to matching diffusivities, ONLINEOVERLAND effectively minimizes numerical dispersion, i.e., the third-order discretization error, by defining the grid ratio such that the Courant number, in planes and channel, is as close to 1 as possible. The amplitude and phase portraits of the Muskingum-Cunge diffusion wave model have been examined by Ponce and Vuppalapati (2016).

3.  TEST PROBLEM

A reference test problem was chosen for use together with script ONLINEOVERLAND. For a given overland flow modeling problem, the script requires the input of twenty-four (24) parameters, which, taken as a set, describe the geometric and physical characteristics of the overland flow problem.

Table 1 shows the list of twenty-four (24) input parameters, with corresponding values adopted in the reference test problem. Note that the latter is the same as the Sample Input data set considered in the online script. For added clarity, in Column 3 (Value), the following rows are labeled with a large red asterisk (*):

  • Row 11 (overland flow area A),
  • Row 13 (slope of left plane Slp).
  • Row 15 (rating exponent for left plane βlp), and
  • Row 20 (slope of channel Sch).

These parameters are selected to perform sensitivity analysis. The objective is to determine the difference in catchment response (i.e., the outflow hydrograph), between the two types of hydraulic diffusivities considered here: (1) kinematic (Eq. 1); and (2) dynamic (Eq. 4). The results of the sensitivity analysis are presented in Sections 4 to 7.

Table 1.  Input data for reference test problem.
(1) (2) (3)
No. Parameter Value
1 Rainfall depth P 24 cm
2 Runoff curve number CN 100
3 Total rainfall duration tr 12 hr
4 Number of points in cumulative rainfall distribution Np 2
5 Dimensionless cumulative time for rainfall distribution T* 0, 1
6 Dimensionless cumulative depth for rainfall distribution D* 0, 1
7 Total simulation time Tt 48 hr
8 Number of time intervals NΔt 96
9 Number of time intervals for printing Npr 1
10 Fraction used to estimate reference discharge Fr [Default]
11 Overland flow area A 18 ha *
12 Fraction of area in left plane Flp 0.5
13 Slope of left plane Slp 0.001 *
14 Manning coefficient for left plane nlp 0.1
15 Rating exponent for left plane βlp -1 *
16 Slope of right plane Srp [blank]
17 Manning coefficient for right plane nrp [blank]
18 Rating exponent for right plane βrp [blank]
19 Length of channel Lch 400 m
20 Slope of channel Sch 0.01 *
21 Manning coefficient of channel nch 0.015
22 Bottom width of channel Bch 2 m
23 Design depth of channel ych 0.6 m
24 Side slope of channel z [z H :1 V] 3

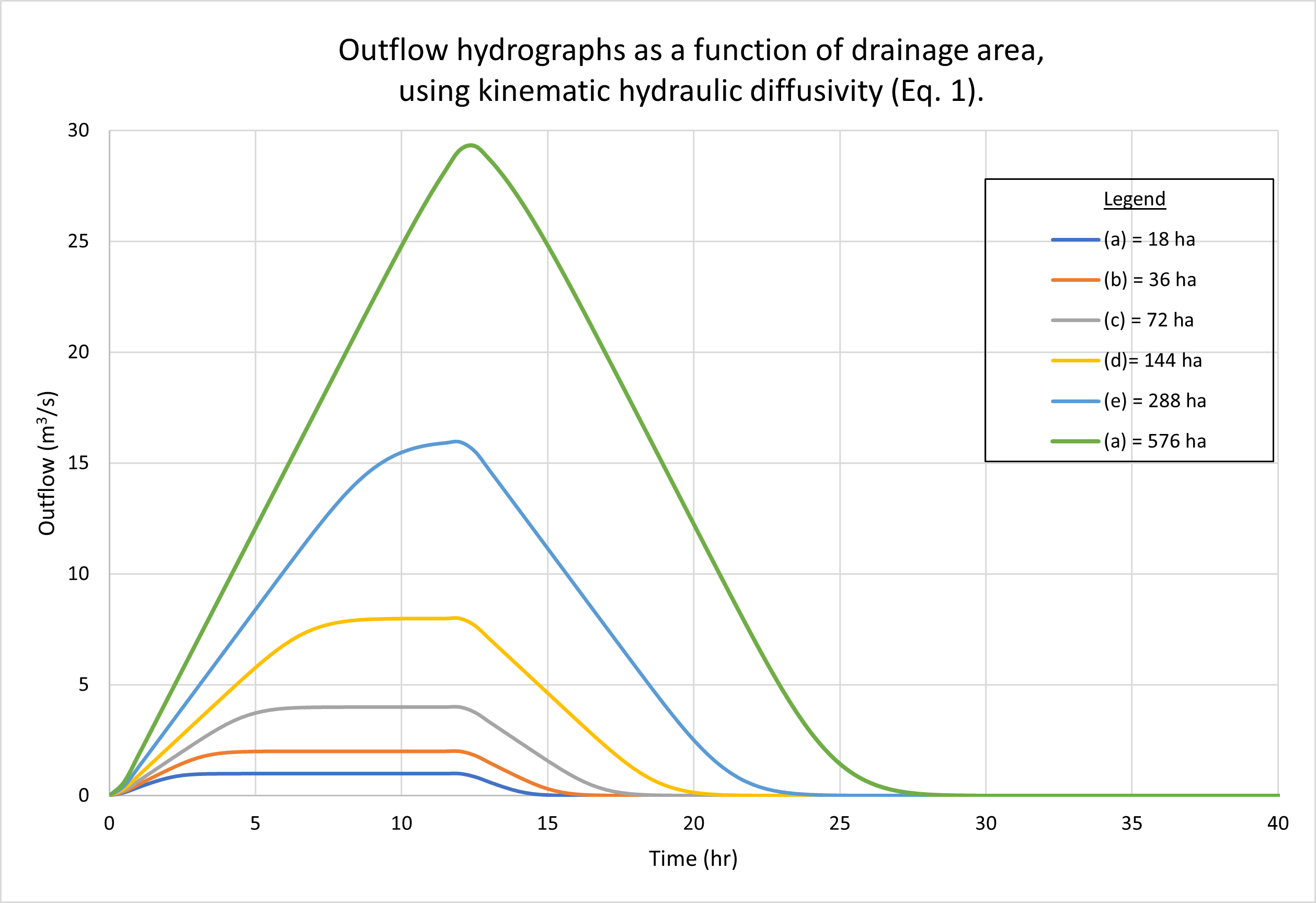
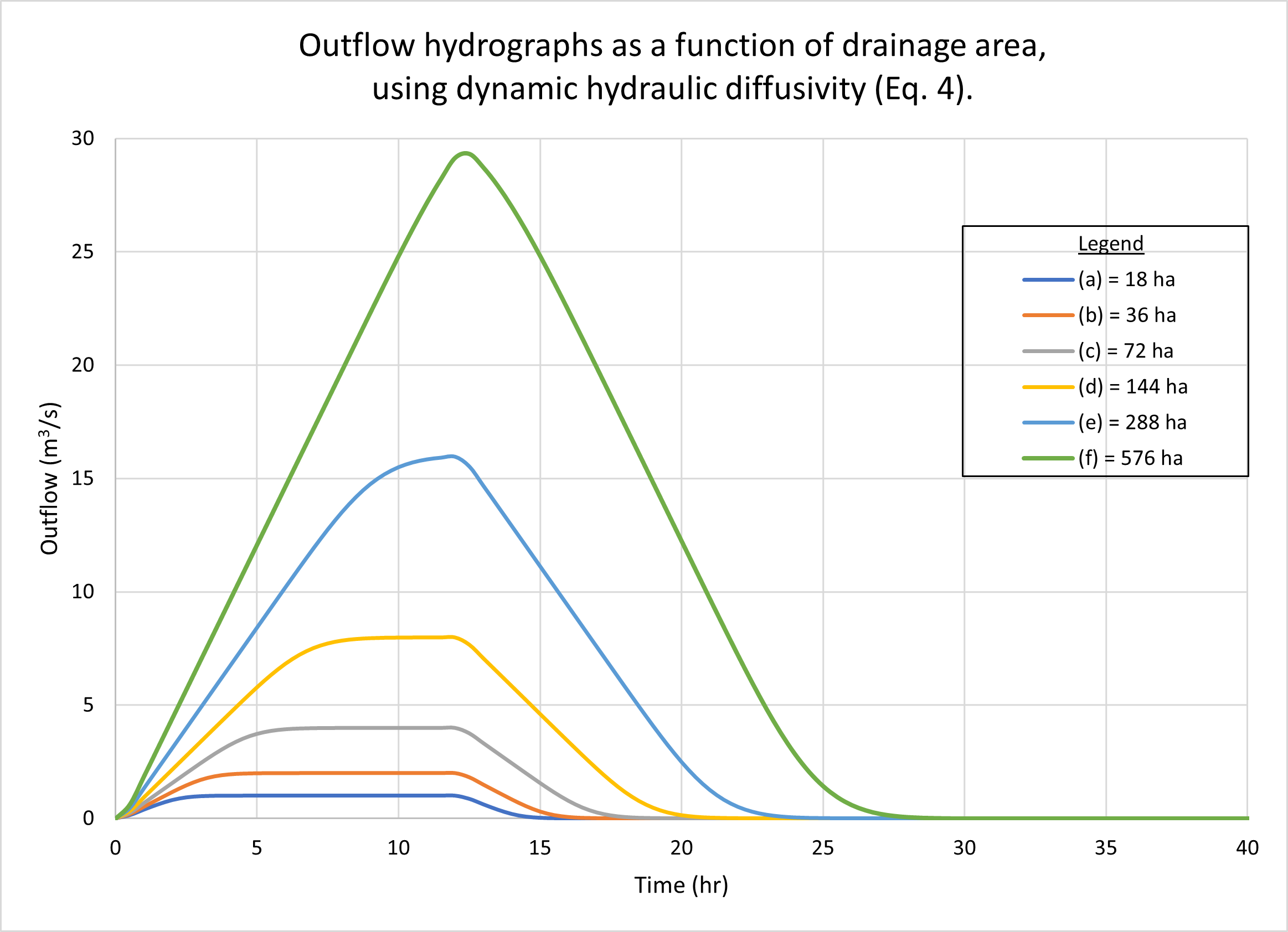
4.  EFFECT OF DRAINAGE AREA

In this section we describe the response of the diffusion wave model of catchment dynamics to the variation of drainage area, i.e., the overland flow area A (Table 1, row 11). We note that the response of the reference test problem (Section 3) is a superconcentrated catchment flow hydrograph, wherein the rainfall duration (12 hr) exceeds the time of concentration (Ponce, 2014a; 2014b). The effective rainfall intensity, corresponding to a curve number CN = 100 (Table 1, row 2), is:

ie = P/tr = 24 cm / 12 hr = 2 cm/hr.

Therefore, the peak flow is:

Qp = ie A = 2 cm/hr × 18 ha = 1 m3/s.

Figure 2 shows the hydrographs calculated by ONLINEOVERLAND for a series of drainage areas, each determined by doubling the previous value, starting with the reference test problem of 18 ha, as follows: (a) 18 ha; (b) 36 ha; (c) 72 ha; (d) 144 ha; (e) 288 ha, and (f) 576 ha. Figure 2 (a) shows the results using the kinematic hydraulic diffusivity (Eq. 1). Fig. 2 (b) shows the results using the dynamic hydraulic diffusivity (Eq. 4). No appreciable difference in catchment response may be observed with the variation in drainage area.

We note that while hydrographs a, b, c, and d are superconcentrated, featuring a typical flat top, hydrograph e is concentrated, with a distinct peak at the maximum possible (16 m3/s), while hydrograph f is subconcentrated, with its peak, close to 29 m3/s, falling short of reaching the maximum possible of 32 m3/s.

Fig. 2 (a)  Outflow hydrograps as a function of drainage area,
using kinematic hydraulic diffusivity (Eq. 1).

Fig. 2 (b)  Outflow hydrograps as a function of drainage area,
using dynamic hydraulic diffusivity (Eq. 4).

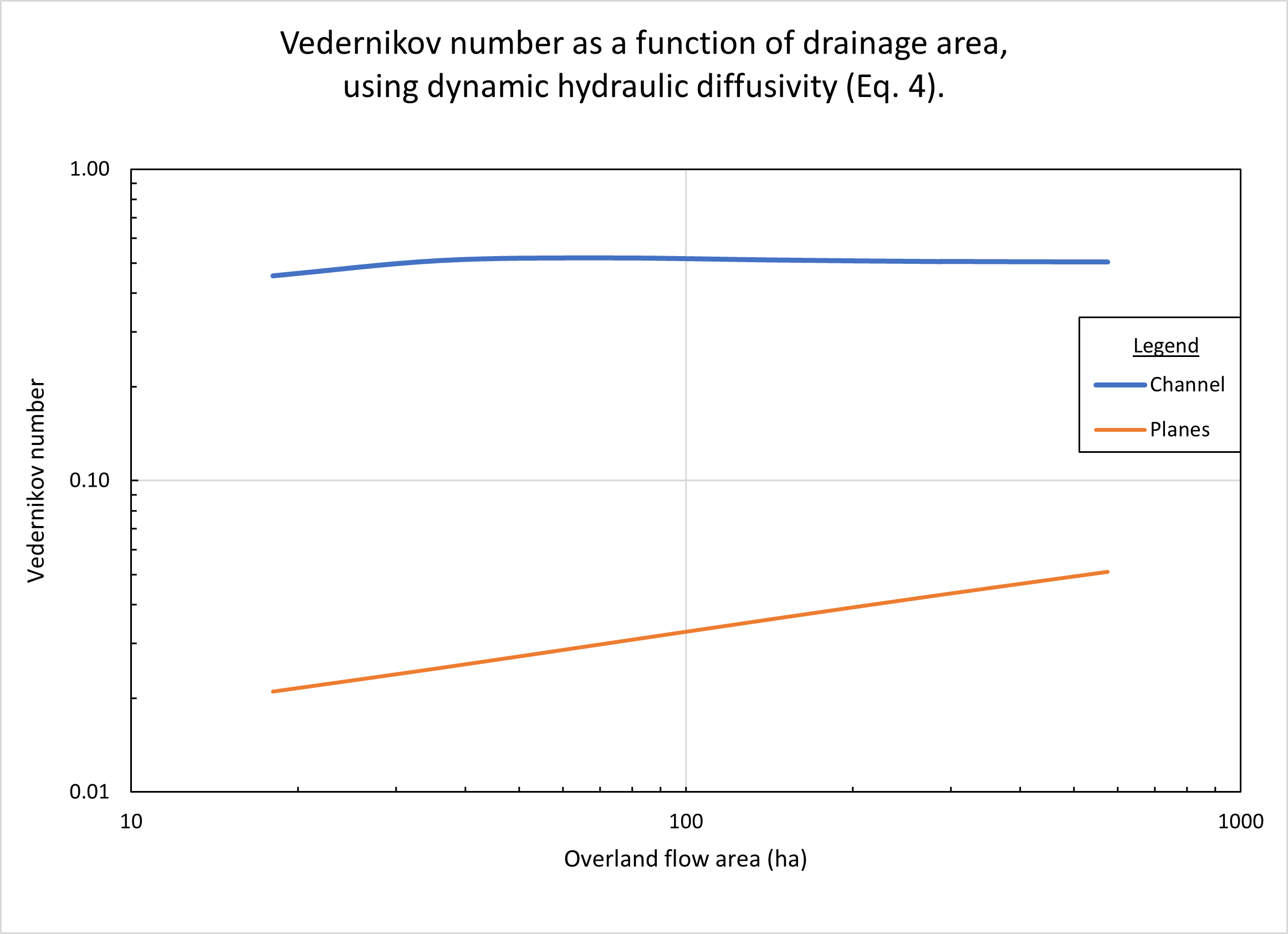
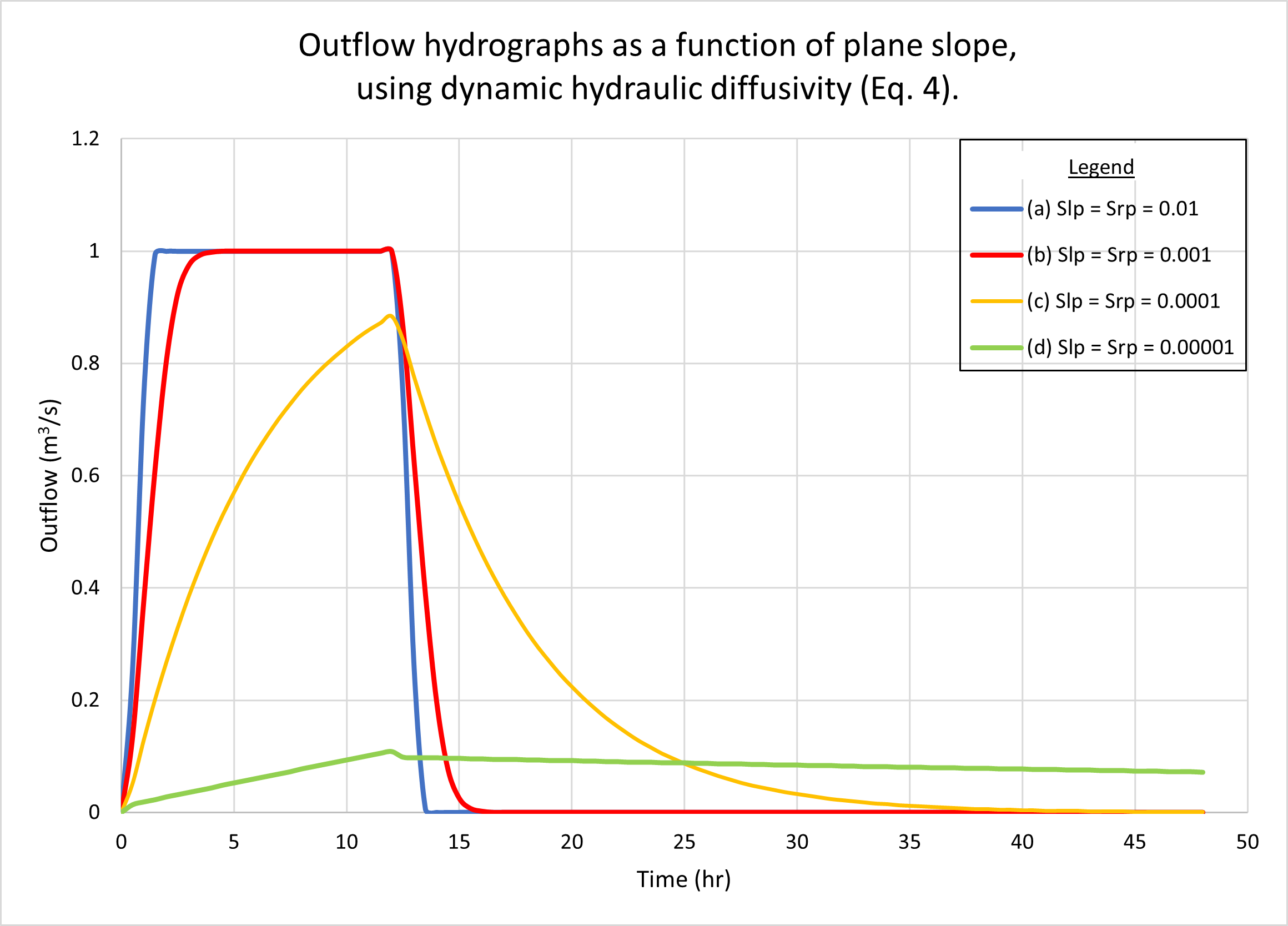
Figure 3 shows the calculated Vedernikov number as a function of drainage area, using the dynamic hydraulic diffusivity (Eq. 4). In order to accomodate the outflow for the larger drainage areas, the design channel depth in the reference test problem (Table 1, line 23) was increased to 1.2 m. In the planes, the Vedernikov numbers are quite low, increasing with an increase in drainage area A, from V = 0.012 for A = 18 ha, to V = 0.05 for A = 576 ha. As expected, in the channel the Vedernikov number is relatively high, around V = 0.5, and remains approximately constant for all tested drainage areas, which vary from 18 to 576 ha.

Fig. 3  Vedernikov number in planes and channel, as a function of plane slope.

5.  EFFECT OF PLANE SLOPE

In this section we describe the response of the diffusion wave model of catchment dynamics to the variation of plane slopes, i.e., the slope of the left plane Slp (Table 1, row 13) and the slope of the right plane Srp (Table 1, row 16). In all cases, it is assumed that Srp = Slp (reference test problem).

As with Section 4, the response of the reference test problem is a superconcentrated catchment flow hydrograph, wherein the rainfall duration (12 hr) exceeds the time of concentration (Ponce, 2014). The effective rainfall intensity, corresponding to a curve number CN = 100 (Table 1, row 2), is:

ie = P/tr = 24 cm / 12 hr = 2 cm/hr.

Therefore, the peak flow is:

Qp = ie A = 2 cm/hr × 18 ha = 1 m3/s.

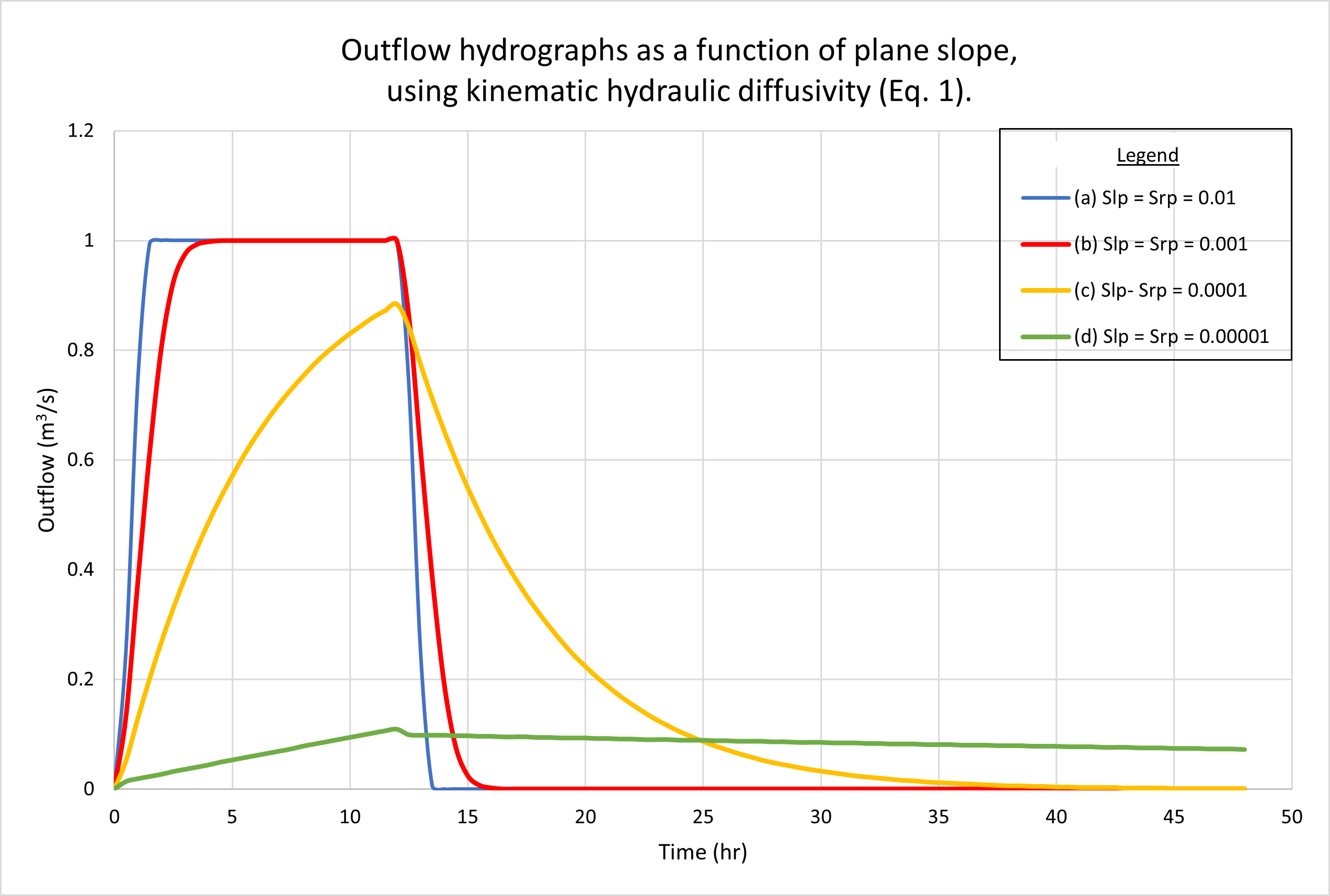
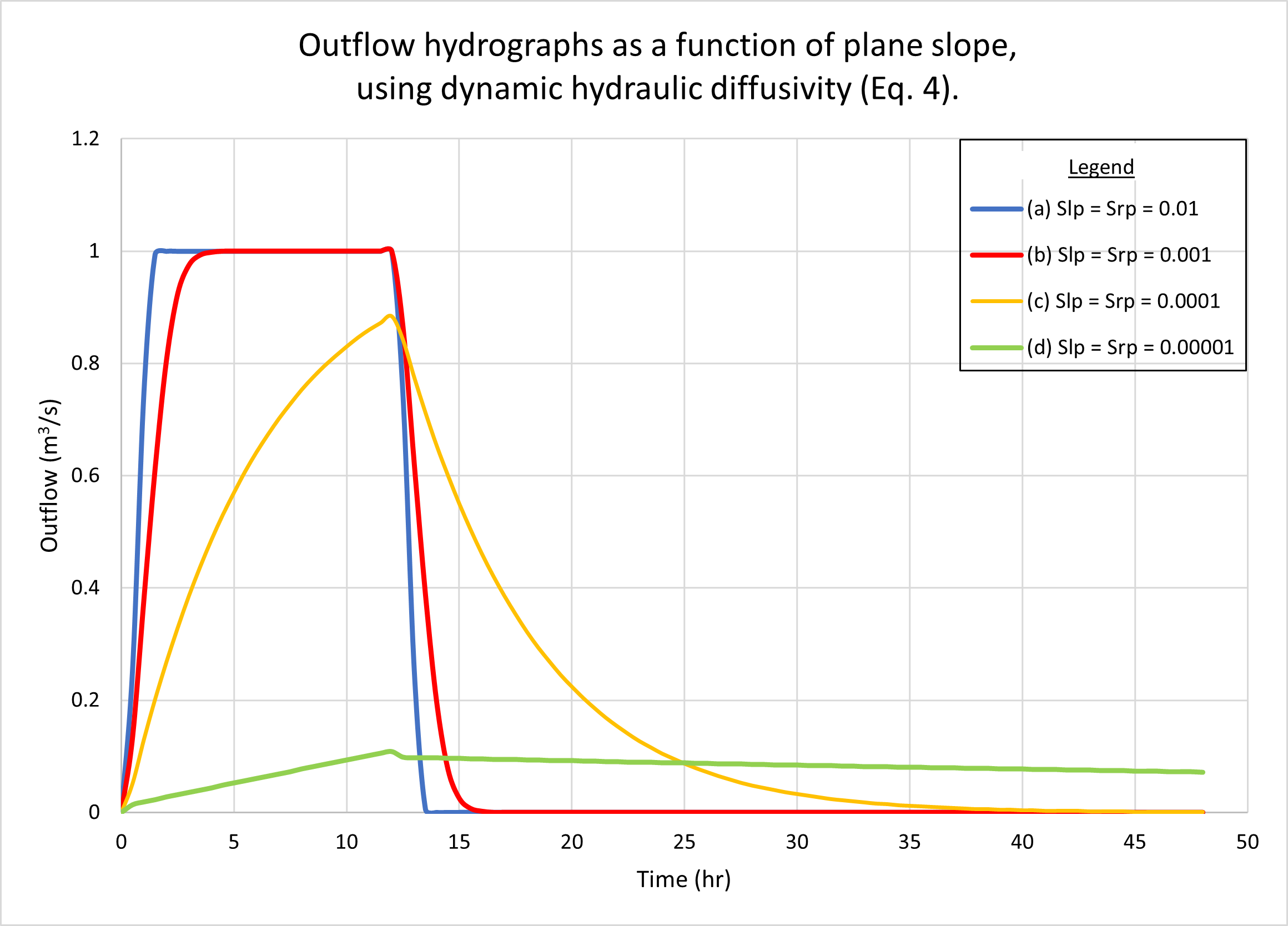
Figure 4 shows the hydrographs calculated by ONLINEOVERLAND for four (4) plane slopes, as follows: (a) 0.01; (b) 0.001; (c) 0.0001, and (d) 0.00001. Figure 4 (a) shows the results using the kinematic hydraulic diffusivity (Eq. 1). Fig. 4 (b) shows the results using the dynamic hydraulic diffusivity (Eq. 4). No appreciable difference in catchment response between the two figures may be observed.

As expected, hydrographs a and b are superconcentrated, featuring the characteristic flat top at 1 m3/s. However, hydrograph c is subconcentrated, with a distinct peak at about 0.88 m3/s, clearly below the maximum possible value of 1 m3/s. Hydrograph d is also subconcentrated, with its peak at about 0.1 m3/s. We reckon that as the plane slopes decrease, the time of concentration increases, eventually exceeding the effective rainfall duration (12 hr), resulting in subconcentrated catchment flow.

Fig. 4 (a)  Outflow hydrographs as a function of plane slopes,
using kinematic hydraulic diffusivity (Eq. 1).

Fig. 4 (b)  Outflow hydrographs as a function of plane slopes,
using dynamic hydraulic diffusivity (Eq. 4).

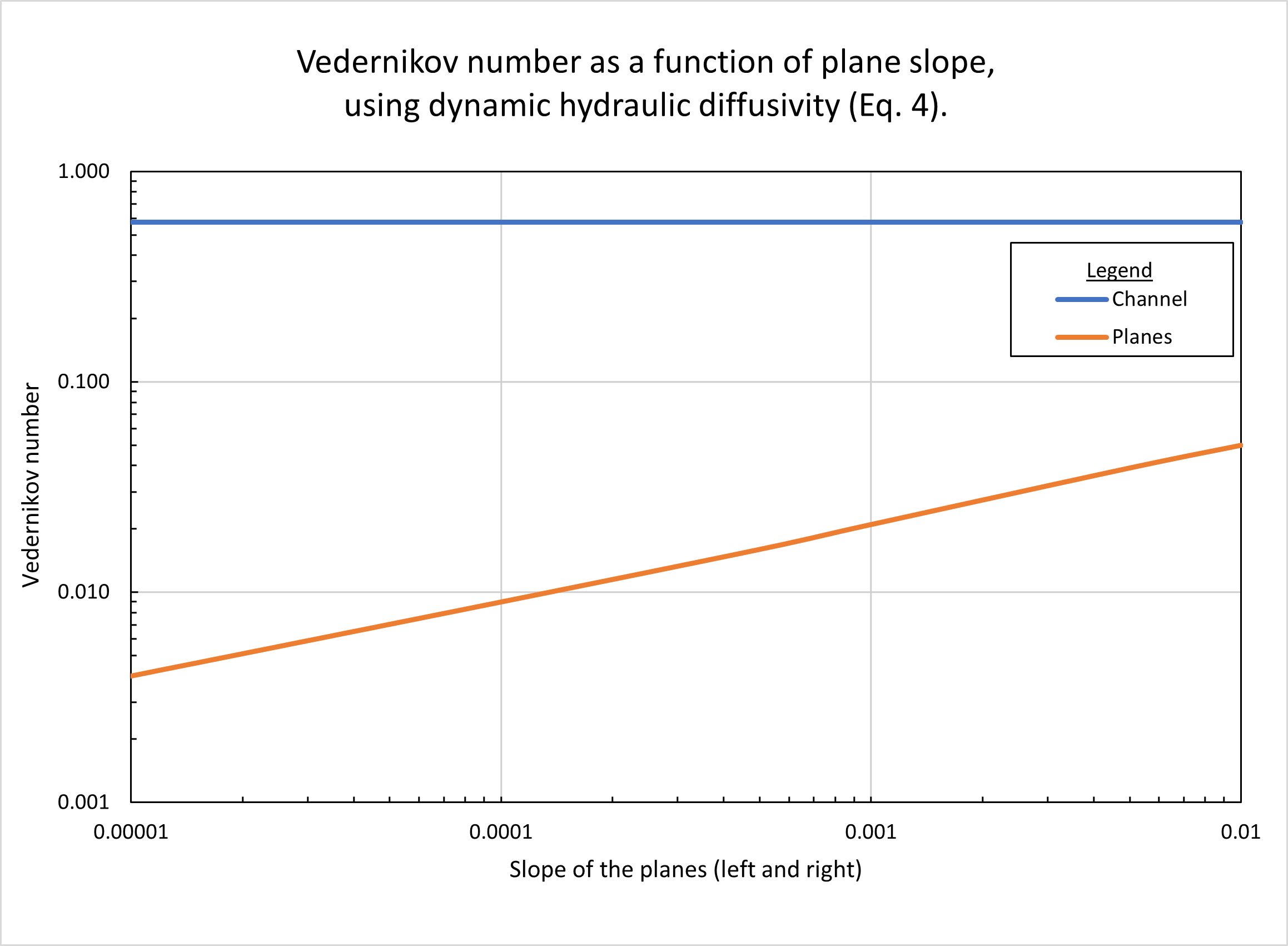
Figure 5 shows the calculated Vedernikov number, as a function of plane slope, using the dynamic hydraulic diffusivity (Eq. 4). In the planes, Vedernikov numbers are quite low, increasing with an increase in slope, from V = 0.004 for a slope Sp = 0.00001, to V = 0.05 for a slope Sp = 0.01. In the channel, the Vedernikov number is high (V = 0.58) and remains constant (with the variation in plane slope), since the relatively high channel slope (Sch = 0.01) is constant and corresponds to the reference test problem (Table 1, row 20).

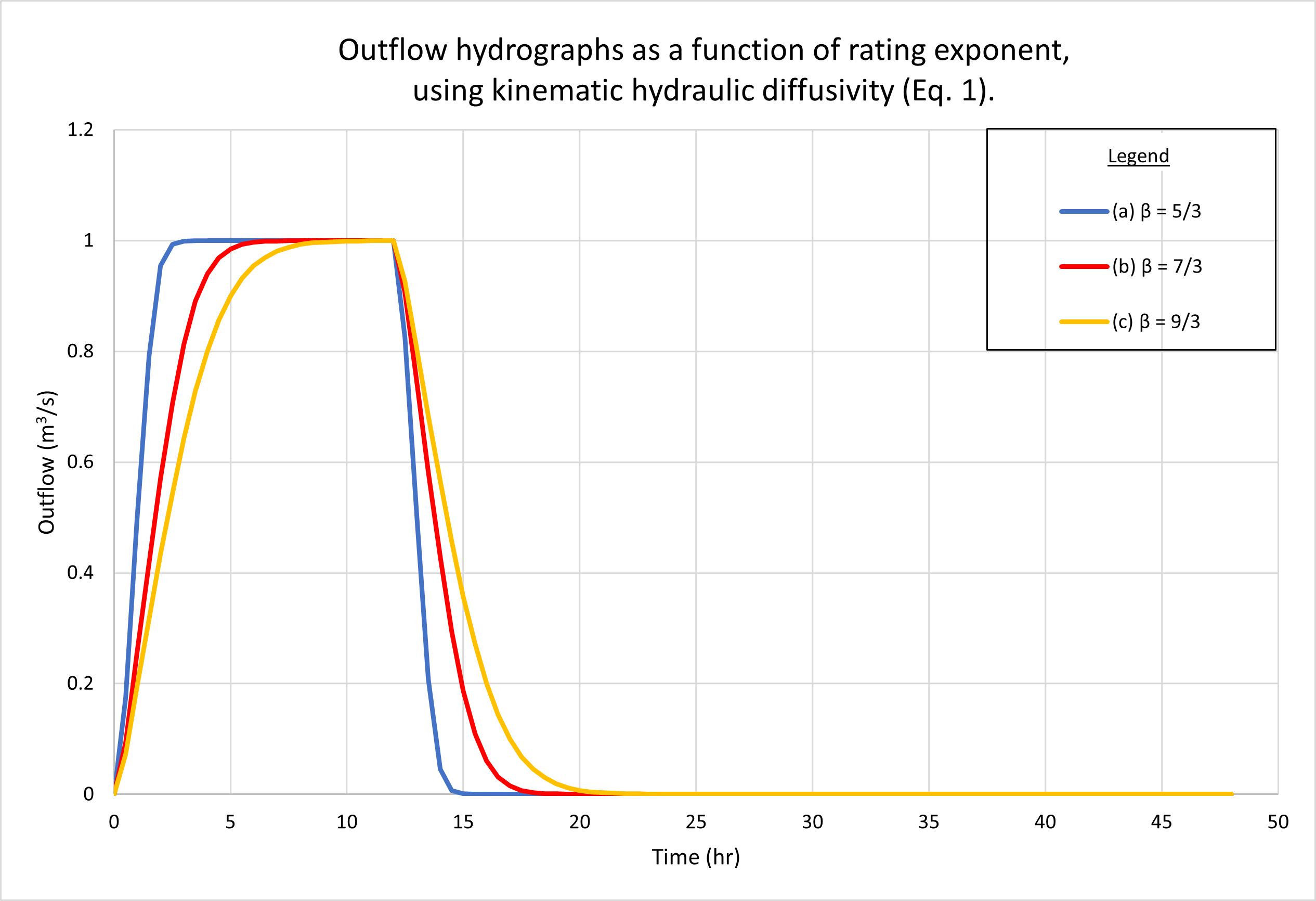
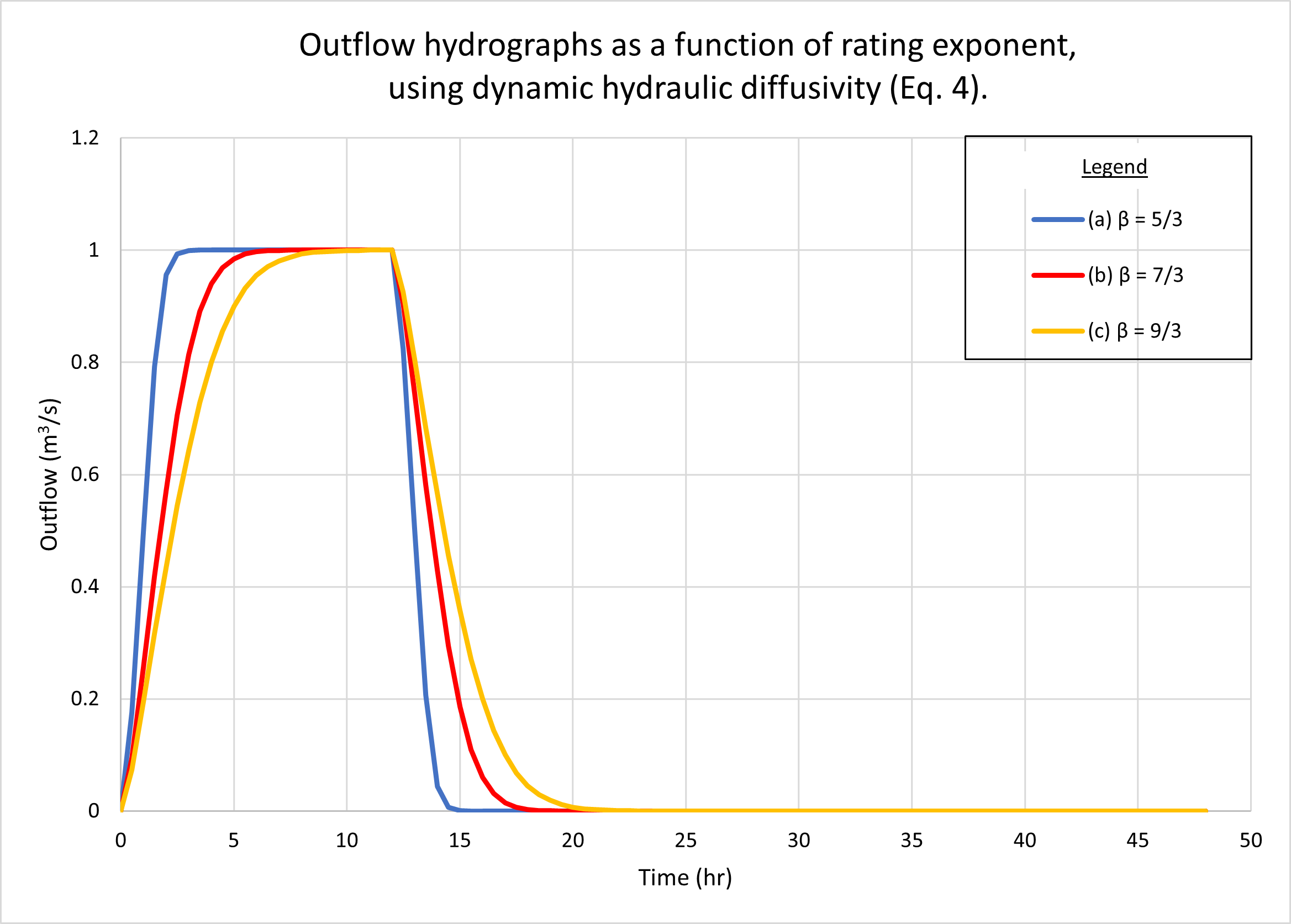
Fig. 5  Vedernikov number in planes and channel, as a function of plane slope.

6.  EFFECT OF RATING EXPONENT

In this section we describe the response of the diffusion wave model of catchment dynamics to the variation in rating exponent β. In free-surface flow, the latter varies with the type of friction and cross-sectional shape (Ponce, 2014c). We select three values of β, all three corresponding to a hydraulically wide channel, varying the type of bottom friction as follows: (1) turbulent Manning, β = 5/3; (2) mixed 50% laminar - 50% turbulent Manning, β = 7/3; and (3) laminar, β = 9/3, i.e., β = 3.

Figure 6 shows the hydrographs calculated by ONLINEOVERLAND. Figure 6 (a) shows the results using the kinematic hydraulic diffusivity (Eq. 1). Fig. 6 (b) shows the results using the dynamic hydraulic diffusivity (Eq. 4). No appreciable difference in catchment response between the two figures may be observed.

Note that all three hydrographs, a, b, and c, are superconcentrated, featuring the characteristic flat top at 1 m3/s. However, the amount of hydrograph diffusion (in this case, an increase in the hydrograph time base) increases with the value of β (from β = 5/3, turbulent Manning, to β = 9/3, laminar). These results resemble those of Aguilar (2014).

Fig. 6 (a)  Outflow hydrographs as a function of rating exponent,
using kinematic hydraulic diffusivity (Eq. 1).

Fig. 6 (b)  Outflow hydrographs as a function of rating exponent,
using dynamic hydraulic diffusivity (Eq. 4).

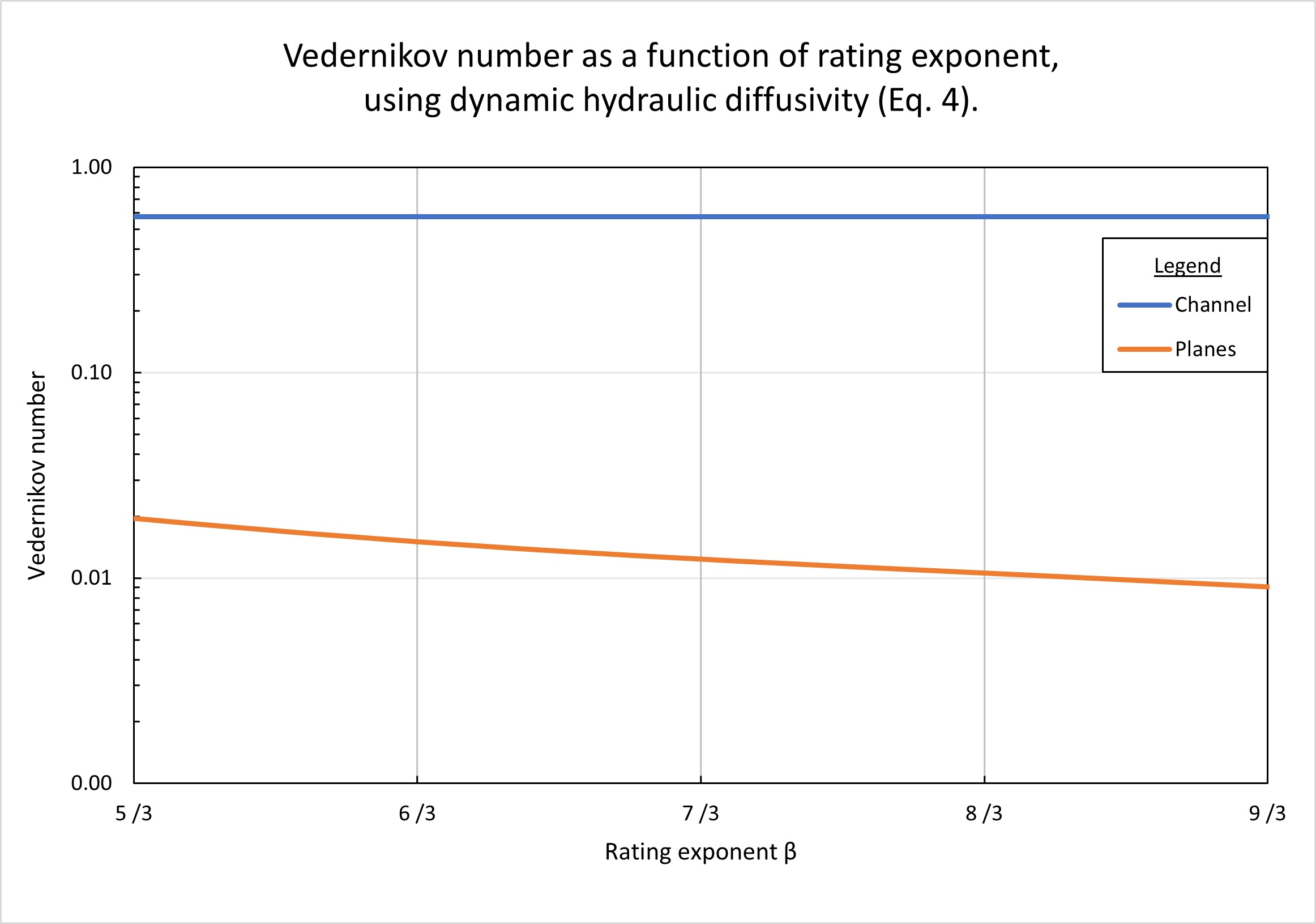
Figure 7 shows the calculated Vedernikov number as a function of rating exponent β, using the dynamic hydraulic diffusivity (Eq. 4). In the planes, Vedernikov numbers are quite low, decreasing with an increase in β, from V = 0.02 for β = 5/3 (turbulent Manning), to V = 0.0085 for β = 9/3 (laminar flow). In the channel, the Vedernikov number is high (V = 0.58) and remains constant (with the variation in rating exponent in the planes), since the relatively high channel slope (Sch = 0.01) is constant and corresponds to the reference test problem (Table 1, row 20).

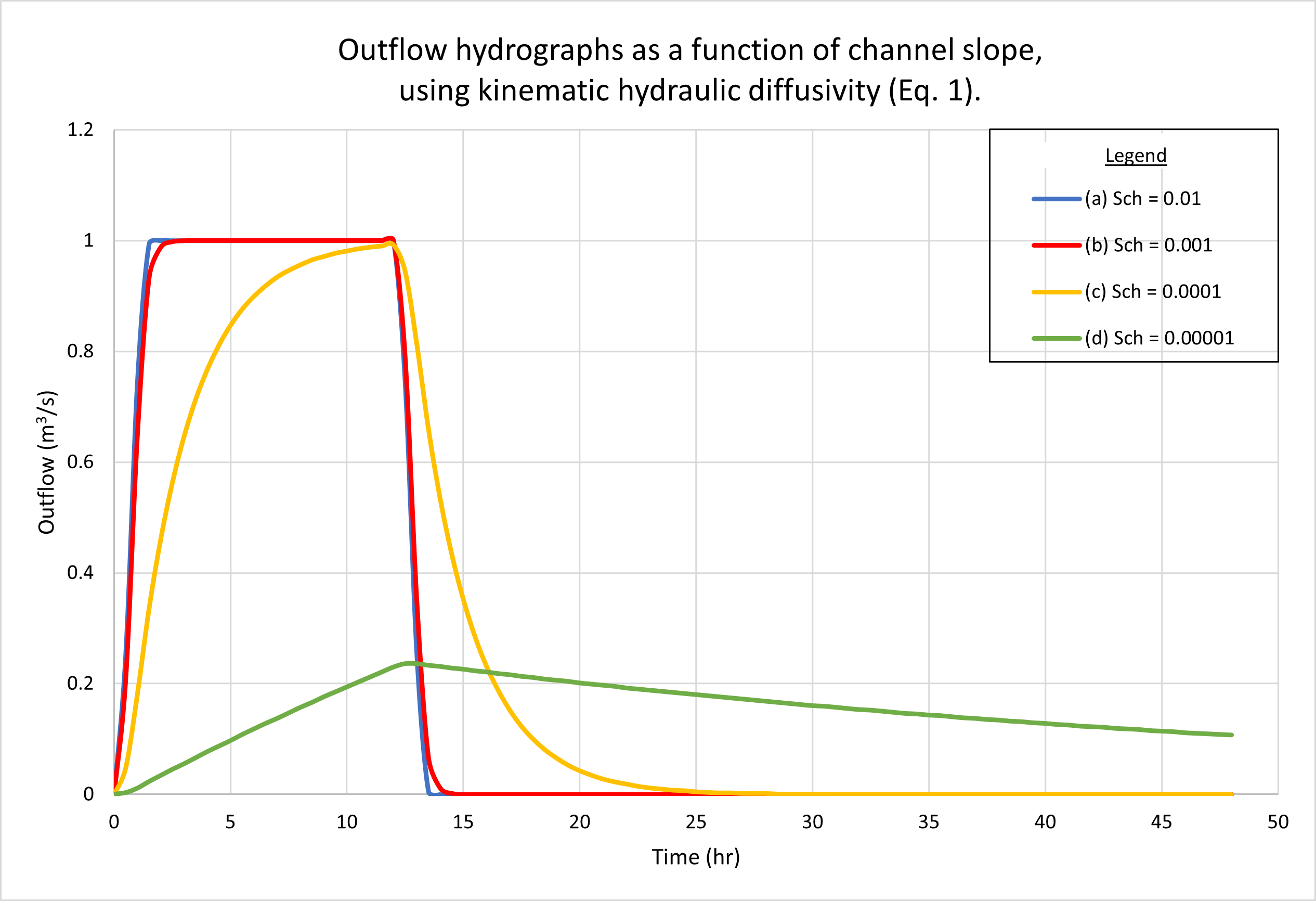
Fig. 7  Vedernikov number as a function of rating exponent.

7.  EFFECT OF CHANNEL SLOPE

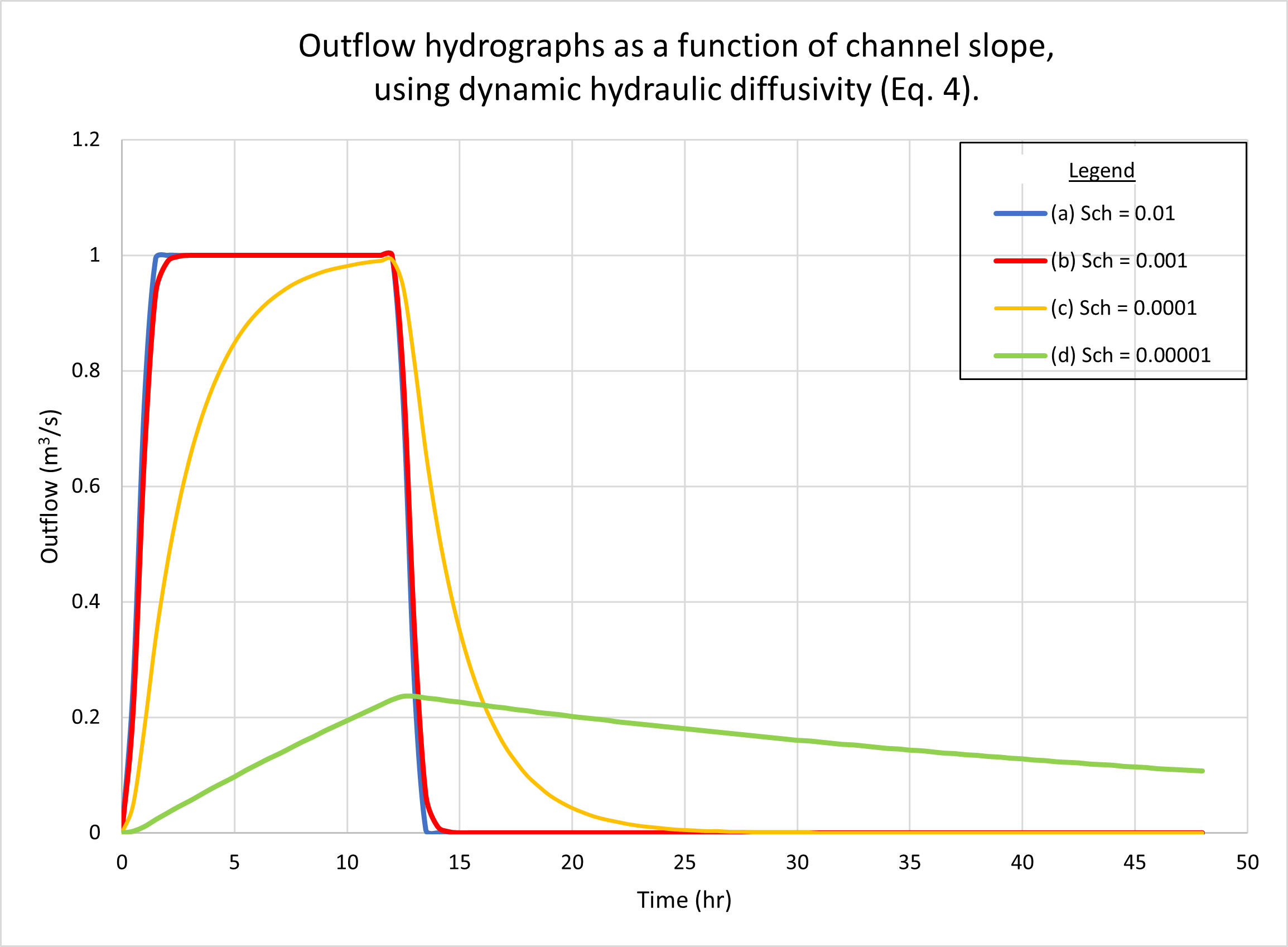
Figure 8 shows the hydrographs calculated by ONLINEOVERLAND for four (4) channel slopes, as follows: (a) 0.01; (b) 0.001; (c) 0.0001, and (d) 0.00001. Figure 8 (a) shows the results using the kinematic hydraulic diffusivity (Eq. 1). Fig. 8 (b) shows the results using the dynamic hydraulic diffusivity (Eq. 4). No appreciable difference in catchment response between the two figures may be observed.

As expected, hydrographs a and b are superconcentrated, featuring the characteristic flat top at 1 m3/s. Hydrograph c is weakly superconcentrated, with a distinct narrow peak at close to 1 m3/s, Hydrograph d is heavily subconcentrated, with its peak at about 0.24 m3/s. We reckon that as the plane slopes decrease, the time of concentration increases, eventually exceeding the effective rainfall duration (12 hr), resulting in subconcentrated catchment flow.

Fig. 8 (a)  Outflow hydrographs for various channel slopes.

Fig. 8 (b)  Outflow hydrographs for various channel slopes.

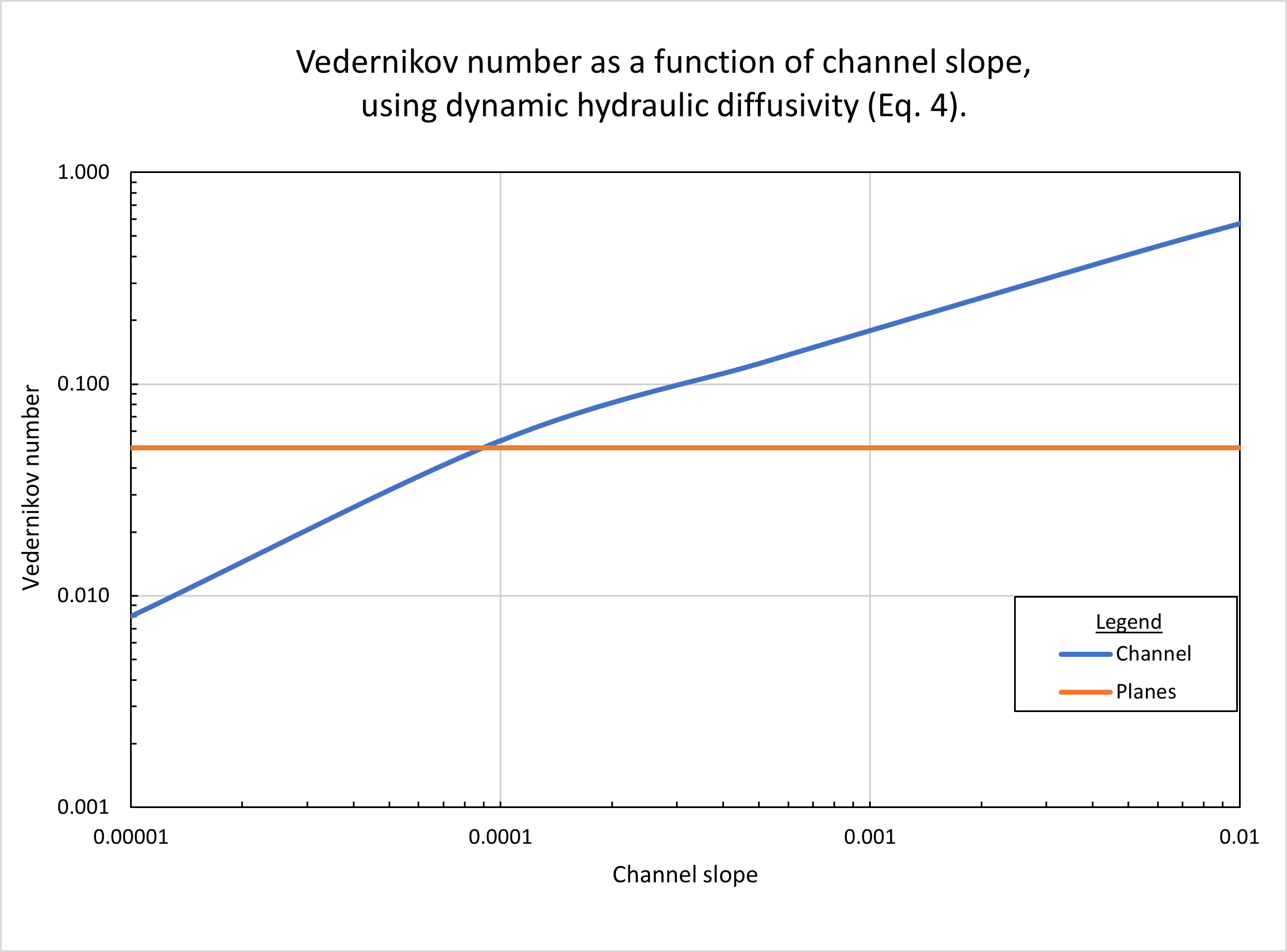
Figure 9 shows the calculated Vedernikov number as a function of channel slope, using the dynamic hydraulic diffusivity (Eq. 4). In the planes, Vedernikov numbers remain constant and equal to V = 0.05, since the plane slopes have not changed: Slp = Srp = 0.001, corresponding to the reference test problem (Table 1, rows 13 and 16, respectively). As expected, in the channel the Vedernikov numbers increase sharply, from V = 0.008 for a very mild channel slope (Sch = 0.00001), to V = 0.55 (near critical flow) for a relatively steep slope (Sch = 0.01).

Fig. 9  Vedernikov number as a function of channel slope.

8.  ANALYSIS

The results of Sections 4 to 7 have clearly shown that the difference in outflow hydrographs between the two formulations for hydraulic diffusivity (kinematic, Eq. 1; and dynamic, Eq. 4), is negligible for the tested flow conditions listed in Table 1. The reason for this behavoir strikes at the core of shallow wave propagation mechanics (Ponce, 2019). Kinematic waves do not diffuse; therefore, for kinematic waves, any difference in the way diffusion is calculated (i.e., Eq. 1 vs. Eq. 4) would be negligible. Conversely, for diffusion waves, any difference in the way diffusion is calculated would be small. Furthermore, for mixed kinematic-dynamic waves, any difference in the way diffusion is calculated would be substantial.

The wave tested in the reference test problem (Table 1) is a typical wave found in hydrologic practice; therefore, it is very likely to be kinematic. To prove this assertion, we use the kinematic wave applicability criterion developed by Ponce et al. (1978), which is given by the following inequality: T So (uo /do) ≥ 171. For the reference test problem, the hydrograph duration is T = 12 hr, and the channel slope is So = 0.01. The applicable values of mean velocity uo and flow depth do, based on the channel dimensions (Table 1, rows 22 and 24) are the following: uo = 2 m/s, and do = 0.2 m. This leads to: T So (uo /do) = 4320 ≥ 171, confirming that the tested wave is decidedly kinematic.

We reckon that diffusion and mixed kinematic-dynamic waves are more likely to be present in unusual situations, appearing to be the exception rather than the rule (Lighthill and Whitham, 1955). However, we recognize that Eq. 4 is more complete than Eq. 1 in describing the dynamics of the flow phenomena, and that it will correctly solve, without any undue additional complexity, all types of waves, including kinematic, diffusion, and mixed kinematic-dynamic. Therefore, we submit that Eq. 4 should be the preferred way to calculate the coefficient of hydraulic diffusivity in diffusion wave modeling of catchment dynamics.

9.  SUMMARY

Two existing formulations for the coefficient of hydraulic diffusivity in diffusion wave modeling of catchment dynamics (Eqs. 1 and 4) are evaluated and compared. While the kinematic hydraulic diffusivity (Eq. 1) is independent of the Vedernikov number, the dynamic hydraulic diffusivity (Eq. 4) is dependent on the Vedernikov number. We use the script ONLINEOVERLAND, an analytical tool capable of considering either the kinematic (Eq. 1) or dynamic (Eq. 4) approaches to model hydraulic diffusivity. The objective is to compare the behavior of these two approaches in generating outflow hydrographs for catchment open-book configurations. For this purpose, we use the reference test problem described in Table 1.

Testing of the model varying the drainage area A, plane slopes Slp and Srp, rating exponent β, and channel slope Sch, show the model's consistency in simulating catchment response under a variety of flow conditions. Calculated outflow hydrographs correctly show the type of catchment response, showing either superconcentrated, concentrated, or subconcentrated catchment flow, depending on the input data.

The reference test problem is confirmed to depict a kinematic wave, effectively featuring zero wave diffusion. Therefore, the differences in outflow hydrograph between the two hydraulic diffusivities (kinematic, Eq. 1, and dynamic, Eq. 4) are shown to be negligible (Figs. 2, 4, 6, and 8). Furthermore, for the general problem, which includes all types of shallow-water waves, i.e., kinematic, diffusion, and mixed kinematic-dynamic, the use of the dynamic hydraulic diffusivity is recommended, since it is more theoretically appealing than its kinematic counterpart, without significantly increasing the modeling complexity.

REFERENCES

Aguilar, R. D. 2014. Diffusion wave modeling of catchment dynamics using online calculation. M.S. Thesis, Department of Civil, Construction, and Environmental Engineering, San Diego State University, San Diego, California; online version.

Cunge, J. A. 1969. On the Subject of a Flood Propagation Computation Method (Muskingum Method), Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.

Dooge, J. C. I. 1973. Linear theory of hydrologic systems. Technical Bulletin No. 1468, U.S. Department of Agriculture, Washington, D.C. Dooge (1973).

Dooge, J. C. I., W. B. Strupczewski, and J. J. Napiorkoswki. 1982. Hydrodynamic derivation of storage parameters in the Muskingum model. Journal of Hydrology, 54, 371-387.

Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December.

Lighthill, M. J., and G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.

Ponce, V. M. 1978. Applicability of kinematic and diffusion models. Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY3, 353-360.

Ponce, V. M. 1986. Diffusion wave modeling of catchment dynamics. Journal of Hydraulic Engineering, ASCE, Vol. 112, No. 8, 716-727.

Ponce, V. M. 1991a. The kinematic wave controversy. Journal of Hydraulic Engineering, ASCE, Vol. 117, No. 4, April, 511-525.

Ponce, V. M. 1991b. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.

Ponce, V. M. 2014a. Engineering Hydrology: Principles and Practices, Section 2.4: Runoff. Online textbook.

Ponce, V., M. 2014b. Runoff diffusion reexamined. Online publication.

Ponce, V. M. 2014c. Fundamentals of Open-channel Hydraulics, Section 1.2: Types of Flow. Online textbook.

Ponce, V., M, and V. Vuppalapati. 2016. Muskingum-Cunge amolitude and phase portraits with online computation. Online publication.

Ponce, V., M. 2019. The S-curve explained. Online publication.

Wooding, R. A. 1965. A hydraulic model for the catchment-stream problem. I. Kinematic wave theory. Journal of Hydrology, Vol. 3, Nos. 3/4, pp. 254-267.

220718 14:35