FROUDE AND VEDERNIKOV: PILLARS OF OPEN-CHANNEL HYDRAULICS
Professor Emeritus of Civil and Environmental Engineering
San Diego State University, San Diego,
California
1. INTRODUCTION
Around the beginning of the twentieth century, hydraulic engineering, a branch of civil engineering,
began to experience an accelerated pace of development.
The world's population was increasing, and it was becoming patently clear that
human societies had to rely on the
hitherto novel scientific method
for the utilization and management of water resources. Well in the twentieth century,
the use of the Froude number, developed in England in the 1860s,
became established in hydraulic engineering practice.
The Froude number defined the threshold wherein the mean flow velocity
in an open channel is equal to the relative velocity, i.e., the relative celerity, of a small surface disturbance.
Several decades later, specifically in the middle of the twentieth century (1945-46),
the concept of Vedernikov number arose in the
former
In this article, we will show that the three velocities
defining the two concepts of Froude and Vedernikov are the only
velocities which may be readily identified in the field of open-channel hydraulics.
This fact surely makes these two fundamental concepts the two
pillars on which the entire field of open-channel hydraulics rests. The historical flavor with which we
endeavor to present the topic significantly enhances the theory and goes the extra mile to clarify the technical concepts. We surmise that the profession should be altogether better because of it.
2. WILLIAM FROUDE: A SHORT BIO
William Froude was a distinguished British engineer, hydrodynamicist and naval architect. Born in Dartington, Devon, England on November 28, 1810, he died from a stroke at age 69 on a cruise to Simon's Town, South Africa. He acquired his education in mathematics at Oxford. In 1832, immediately after his graduation, he worked for Isambard Kingdom Brunel, the famed developer of railways, as a surveyor on the Great Western Railway, in England. In 1857, Brunel consulted him on the behavior of the Great Eastern ship at sea; based on Froude's recommendations, Brunel modified the design of the ship to avoid rolling. Starting in 1859, Froude built the first towing tank, using his own resources. He carried out ship model experiments using the tank, first at his home in Paignton, Devon County, and later, in his other home, called Chelston Cross, in Torquay. In 1861, he wrote a paper on the design of ship stability, published in the Proceedings of the Institution of Naval Architects. Between 1863 and 1867, he showed the relation between model and prototype, stating that the frictional resistance was equal in both when the speed V was proportional to the square root of the length L. He called this concept the Law of Comparison:
wherein k is a constant that applies to both model and prototype. Equation 1 is known as Froude's law. Froude was the first to identify the most efficient shape for the hull of ships, as well as to predict ship stability based on reduced-scale models (Fig. 1). In open-channel hydraulics, Froude's law is embodied in the Froude number, defined as follows:
in which V = mean flow velocity,
D = hydraulic depth,
and g = gravitational acceleration.

The models were built by Froude to establish resistance and scaling laws for ship design.
3. VALENTIN V. VEDERNIKOV: A SHORT BIO
Valentin Valentinovich Vedernikov,
doctor of technical science (Russian/Soviet terminology; a step above PhD in the Western world), graduated from Don's Polytechnical Institute
(City of Novocherkassk, Rostov Oblast Region) in 1928.
In 1934, Vedernikov published a book entitled Seepage from channels, in which he used a method of conformal images for non-pressurized steady motion of ground water in a vertical plane. In this book he used, for the first time, the method of Vedernikov-Pavlovskiy. The latter is based on conformal imaging of flow regions in the plane of complex potential of velocity of seepage and the Zhukovkiy complex function.
In 1935, Vedernikov was granted the
Ph.D. without defending his dissertation;
in 1938 he defended his dissertation and received the degree of
Doctor of Technical Sciences.
In 1940-1941, Vedernikov was chair of the Department
of Hydraulics and Hydromachinery at the Moscow
Institute of Turf. In 1941-1942
he was working in the Institute of Mechanics of the USSR
Academy of Sciences. Beginning in 1943,
he worked at the Section of Scientific
Research in Hydraulics of the Soviet Academy of Sciences.
In 1945-1947, Vedernikov, theoretically, and later experimentally,
explained the phenomenon of unsteady flow of water
in channels with roll wave formation, defining
the criterion for the instability of flow (Fig. 2).
To accomplish this task, he used the Saint-Venant equations of unsteady open-channel
flow.
4. VELOCITIES IN OPEN-CHANNEL FLOW
Steady flow: Mean velocity
There are three distinctive velocities in open-channel flow (Ponce, 1991). The first is the
mean velocity of the steady flow, herein referred to as u. This velocity is calculated using
the Chezy or Manning equations
u = C (RS) 1/2
in which u = mean velocity of the steady uniform (equilibrium) flow, with units of L/T
(m/s or fps);
The Manning formula in the SI system of units is the following
(Manning, 1889):
u = (1/n) (R) 2/3 S1/2
in which u = mean velocity of the steady uniform flow, in m/s; n = Manning
coefficient;
and R (in m) and
u = (1.486/n) (R) 2/3 S1/2
in which R (in ft) and S (in ft/ft).
While the Manning equation is usually preferred in engineering practice, the Chezy equation
may be readily expressed
in dimensionless form, clearly a definite advantage, particularly for theoretical studies
Equations 3 to 5 calculate the mean flow velocity u, i.e., the velocity of steady uniform, or equilibrium, flow. The remainder of this section will describe the two other velocities relevant in open-channel flow, i.e., the velocities, or more properly, celerities, that characterize unsteady flow. Unsteady flow: Two wave celerities
There are two wave celerities which complete the triad of velocity/celerities in open-channel flow:
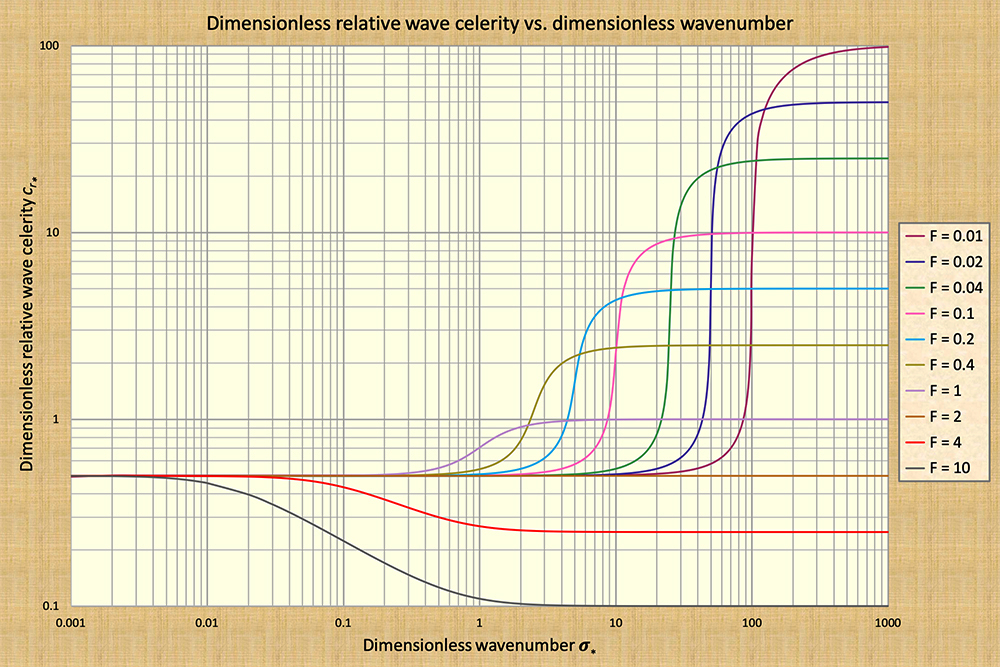
The difference between kinematic and dynamic waves is admirably depicted in the plot of dimensionless relative wave celerities vs. dimensionless wavenumbers (Fig. 3). Kinematic waves plot to the left, while dynamic waves plot to the right. From a historical perspective, kinematic waves are those of Seddon (1900); dynamic waves are those of Lagrange (1788). Wave attenuation for either kinematic or dynamic waves is too small or nonexistent, because the dimensionless relative wave celerities (in the ordinates) in both extremes of the spectrum (left and right) remain constant and independent of dimensionless wave number (in the abscissas).
The kinematic wave celerity is: ck = β u,
in which β is the exponent of the discharge-flow area rating
The dynamic wave celerity has two components: cd = u ± (gD)1/2,
in which g = gravitational acceleration,
D = hydraulic depth = A /T
(Ponce, 2014: Chapter 1).
Therefore, the relative dynamic wave celerity
(i.e., the celerity relative to the mean flow velocity) is:
crd = w = (gD)1/2.
In summary, the three velocities (one velocity and two celerities) preeminent in open-channel flow, including both
steady and unsteady flow,
are: (1)
We will show here that these three velocities/celerities (u,
v, and w)
may produce only two independent dimensionless numbers:
5. THE FROUDE NUMBER
The Froude number is defined as the ratio of the mean flow velocity u to the relative celerity of dynamic waves w (Ponce, 1991):
F = u /w
In other words, the Froude number compares the mean velocity of the flow to the relative
celerity (speed) of small (dynamic) surface perturbations. Three situations are possible:
For w > u, then F < 1,
and the flow is in a subcritical state. Since w > u, the result of (u - w) < 0,
and the perturbation is able to travel upstream; consequently, the flow may
be controlled only from a downstream location.
For w = u, then F = 1,
and the flow is in a critical state. Since w = u, the result of (u - w) = 0,
and the perturbation remains stationary; it is not able to travel either upstream or downstream.
For w < u, then F > 1,
and the flow is in a supercritical state. Since w < u,
the result of
6. THE VEDERNIKOV NUMBER
The Vedernikov number is defined as the ratio of the relative celerity of kinematic waves
v to the relative celerity of dynamic waves w (Ponce, 1991):
V = v /w
In other words, the Vedernikov number compares the relative celerity of
"large" (of small dimensionless wavenumber) kinematic waves,
i.e., those driven by mass gradients, to the relative
celerity of "small" (of large dimensionless wavenumber)
dynamic waves, i.e., those driven by energy gradients For w > v, then V < 1,
and the flow is in stable state. Since w > v, it follows that
(w - v) > 0;
consequently, the primary energy disturbance, traveling downstream (with relative dynamic wave celerity
w) travels faster than the mass disturbance (with relative kinematic wave celerity v).
For w = v, then V = 1,
and the flow is in neutrally stable state. Since w = v, it follows that For w < v, then V > 1,
and the flow is in unstable state. Since w < v, it follows that (w - v) < 0;
consequently, the primary energy disturbance, traveling downstream (with relative dynamic wave celerity
w), travels slower than the mass disturbance (with relative kinematic wave celerity v).
The above statements are summarized in Table 3.
Fig. 5 Roll waves traveling in a steep irrigation canal,
Cabana-Mañazo, Puno, Peru.
7. THE EXPONENT OF THE RATING
The third relation of a total of three [besides (1) F = u /w, and
(2) V = v /w] is: (3)
v /u;
effectively, the third relation is: v /u =
V/F = v /u
Note that the kinematic wave celerity (Section 4) is: ck = βu,
in which β is the exponent of the discharge-flow area rating
V/F = β - 1
In other words, the exponent β
of the rating (Q = αAβ) encapsulates the Froude and Vedernikov numbers, such that β = (V/F) + 1.
Furthermore, for V = 1, i.e., for neutrally stable flow,
the neutrally stable Froude number is: Fns = 1 / (β - 1).
For instance, for β = 1.5,
i.e., for Chezy friction in a hydraulically wide channel: Fns = 2. This finding is confirmed by Fig. 3,
wherein the full horizontal line, applicable for F = 2, remains constant for all wave sizes, kinematic and dynamic,
and neither attenuates nor amplifies (F = 2 corresponds to the neutrally stable state, applicable for
Chezy friction in hydraulically wide channels).
Table 4 shows the variation of the neutrally stable Froude number Fns
with the exponent β
The above conclusions merit the elevation of the exponent of the rating β to a singular and privileged
position in the field of open-channel hydraulics. The exponent β contains both Froude and Vedernikov numbers
exclusively, while going the extra mile to describe both friction and cross-sectional properties (Table 3).
We reckon that the Vedernikov number varying with friction and cross-sectional shape
is the original finding of Vedernikov (1945,
1946), although he did not quite present
it in a similar way
8. CONCLUDING REMARKS
We have shown that there are only three velocities (properly, one velocity and two celerities) that
generally characterize
open-channel flow across a wide variety of applications in steady and unsteady flow, including channel design,
flow control, flood routing, and surface-flow instability. These are:
These three velocities give rise to only two independent dimensionless numbers:
(1) Froude number
REFERENCES
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York, NY.
Extract: Page 210.
Lagrange, J. L. de. 1788. Mécanique analytique, Paris, part 2, section II, article 2, 192.
Ponce, V. M. and D. B. Simons. 1977.
Shallow wave propagation in open channel flow.
Journal of Hydraulic Engineering ASCE, 103(12), 1461-1476.
Ponce, V. M. 1991. New perspective on the Vedernikov number.
Water Resources Research, 27(7), 1777-1779.
Ponce, V. M. 2014.
Fundamentals of Open-channel Hydraulics.
Online textbook.
Ponce, V. M. and B. Choque Guzman. 2019.
The control of roll waves in channelized rivers. Online article.
Ponce, V. M. 2023a.
The states of flow. Online article.
Ponce, V. M. 2023b.
Ths Vedernikov number. Online article.
Powell, R. W. 1948.
Vedernikov's criterion for ultra-rapid flow.
Transactions, American Geophysical Union, 29(6), 882-886.
Seddon, J. A. 1900. River Hydraulics.
Transactions, American Society of Civil Engineers, XLIII(179-243), June;
Vedernikov, V. V. 1945.
Vedernikov, V. V. 1946.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 240528 |