- Critical flow occurs when the following conditions are met:
- The specific energy E is a minimum for a given discharge Q.
- Discharge Q is a maximum for a given specific energy E.
- The specific force F is a minimum for a given discharge Q.
- Discharge Q is a maximum for a given specific force F.
- The velocity head hv is equal to 1/2 of the hydraulic depth D (D= A/T).
- The Froude number is equal to 1 (F = 1).
- The mean velocity is equal to the relative celerity of small surface perturbations [v = (gD)1/2]

Emergency spillway at Turner reservoir, San Diego County.
|
|
- The flow can be subcritical or supercritical.
- In subcritical flow, the secondary surface perturbation can travel upstream [v < |(gD)1/2|]
- Subcritical flow is controlled from downstream.
- In supercritical flow, the secondary surface perturbation cannot travel upstream [v > |(gD)1/2|]
- Supercritical flow is controlled from upstream.
- In critical flow, the secondary surface perturbation remains stationary [v = |(gD)1/2|]
- Critical state (critical depth) can occur:
- Along the channel: critical channel (critical depth along the channel).
- At a cross section: critical cross section, in either gradually or rapidly varied flow
- The slope of the channel that sustains critical depth is called "critical slope."
- The uniform flow equation in terms of slope, friction coefficient, and Froude number (for a hydraulically wide channel) is:
- f' is 1/8 of the Darcy-Weisbach friction coefficient.
- From now on, we will refer to f' as f.
- For F = 1:
- Thus, the friction coefficient f is equal to the critical slope.
- In other words, f is the critical slope.
- The slope is proportional to the square of the Froude number; the factor of proportionality is f.
- In subcritical flow: So < Sc ⇒ F2 < 1.
- In supercritical flow: So > Sc ⇒ F2 > 1.

Taymi Canal, near Posope Alto, Chiclayo, Peru.
|
|
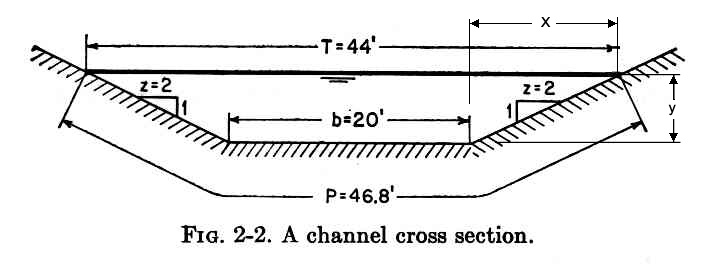
Fig. 2-2 (Chow)
|
|
Example 4-2. Compute the critical depth and velocity of the trapezoidal channel shown above, carrying 400 cfs.
Solution.- The following proportion holds:
z / 1 = x / y
From which: x = zy
T = b + 2x = b + 2zy
A= (1/2) (b + T) y = (1/2) (b + b + 2zy) y = (b + zy) y
D = A/T = [(b + zy) y ] / (b + 2 zy)
V = Q/A
V = (gD)1/2
Q/A = (gD)1/2
Q/(g)1/2 = A(D)1/2 = A(A/T)1/2
Q2/g = A3/T
(Q2/g) T - A3 = 0
[Q2/g] (b + 2zyc) - [(b + zyc) yc ]3 = 0
Divide by 8:
[Q2/(2g)] (b/4 + zyc/2) - [(b/2 + zyc/2) yc ]3 = 0
For Q = 400 cfs, g = 32.2 ft/s2, b = 20 ft, z = 2:
2484 (5 + yc) - [(10 + yc) yc ]3 = 0
Solve by trial and error: yc = 2.15 ft.
Ac = (b + zyc) yc = 52.2 ft2
Vc = Q/Ac = 7.66 fps.
The critical flow equation is:
f(yc) = [Q2/g] (b + 2zyc) - [(b + zyc) yc ]3 = 0
Changing variable to x for simplicity:
x = yc
f(x) = [Q2/g] (b + 2zx) - [(b + zx) x ]3 = 0
To solve this equation by trial and error, the following simple algorithm is suggested:
- Assume x = 0.
- Assume Δx = 1.
- Increment x: x = x + Δx
- Calculate f(x)
- Stop when Δx is small enough (Calculate output variables Ac and Vc).
- If f(x) > 0, return to step 3
- If f(x) < 0, set Δx = 0.1 Δx
- Set x = x - 9 Δx and return to step 4
Example: onlinechannel02.php

USGS stream-gaging station at Campo Creek, near Campo, San Diego County, California.
|
|
- A channel control means the establishment of a definite relationship between the stage and the discharge.
- Channel control is achieved at a control section.
- The control section is a suitable site for a gaging station and to develop the discharge rating curve.
- The Parshall flume forces critical flow at the throat, so that a stable control section can be obtained.

Parshall flume at Cucuchucho constructed wetland, Michoacan, Mexico.
|
|
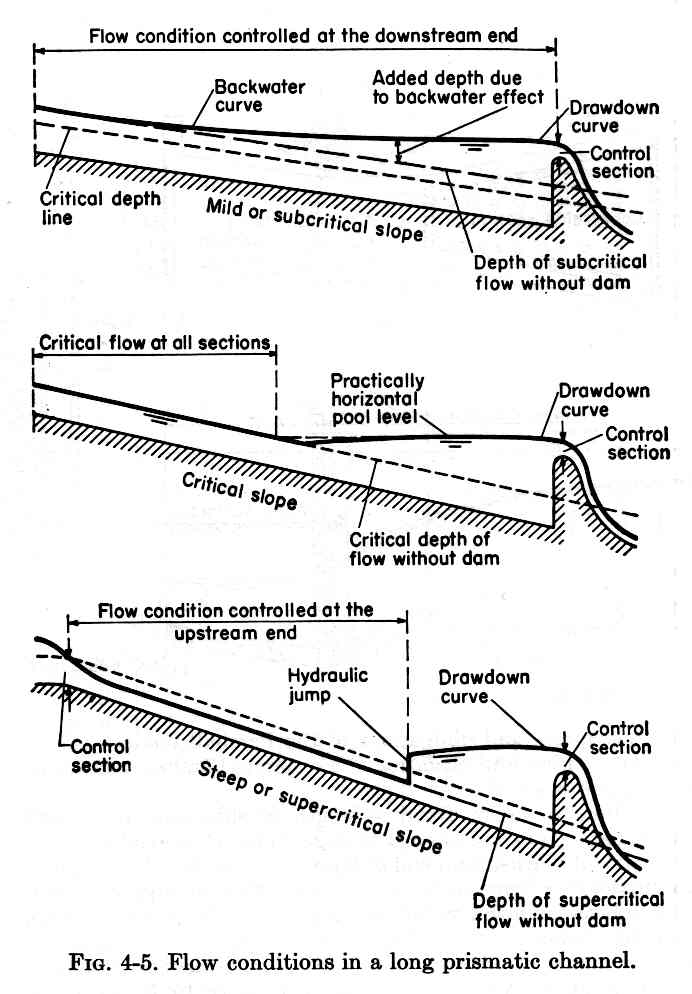
Fig. 4-5 (Chow)
|
|
Example 4-4. Using the theory of critical flow, derive an equation for the discharge over a broad-crested weir.

Detail of 8000-ft weir, Boeraserie Conservancy, Guyana.
|
|
Solution.-
Consider the section on the weir crest where critical flow occurs.
The discharge per unit of width is: q = Vc yc
q = (gyc)1/2 yc
q = (g)1/2 yc3/2
yc = (2/3) He (He = specific energy head at the critical section)
q = (g)1/2 [(2/3) He ]3/2
q = (g)1/2 (2/3)3/2 He 3/2
q = C He 3/2
C = (2/3)3/2 (g)1/2
C = 3.09 in U.S. customary units.
C = 1.7 in SI units.
This is a theoretical equation, since the critical section is usually difficult to locate with certainty.
For practical purposes, the equation is written as:
q = C H3/2
where H is the elevation of the upstream water surface above the weir crest.
This assumes that the approach velocity, at a section sufficiently far from the weir, is Va ≈ 0.
Therefore: H ≈ He
Example: onlinechannel14.php
Crossing the El Cora ford on a motorcycle
Go to Chapter 5.






