|
|
CIVE 530 - OPEN-CHANNEL HYDRAULICS
LECTURE 5: UNIFORM FLOW
|
|
5.1 QUALIFICATIONS FOR UNIFORM FLOW
|
- In uniform flow, the depth, area, velocity and discharge are constant.
- In uniform flow, the slopes are all the same: friction, energy, water-surface, bottom.
- There is no unsteady uniform flow; if the flow is unsteady, it is not uniform.
- At high velocities, the flow becomes unstable and unsteady; this is the instability of uniform flow discussed by Chow.
- Instability of the free surface leads to
roll waves.
- The Vedernikov number V determines the instability.
- At V < 1, uniform (or equilibrium in natural channels) flow can occur.
|
5.2 ESTABLISHMENT OF UNIFORM FLOW
|
- In uniform flow, gravitational forces are entirely balanced by frictional resistance.
- "Nature likes uniform flow."
- The depth of uniform flow is called "normal depth."
- When yn > yc, this is normal subcritical flow.
- When yn < yc, this is normal supercritical flow.
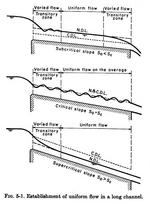
Fig. 5-1 (Chow)
|
|
|
5.3 VELOCITY OF UNIFORM FLOW
|
- The velocity of uniform flow is:
- C is a roughness or friction coefficient.
- Values of x and y vary with roughness and cross-sectional shape.
- According to Manning, the velocity of uniform flow in SI units is:
where n = Manning's n.
- The Manning formula was developed originally in SI units, and later converted to U.S. customary units.
- The Manning formula in U.S. customary units is:
- The constant 1.486 comes from the unit conversion, and it is equal to 1/(0.3048)1/3 = 1.4859
- To compare with Chezy, the Manning formula is expressed as follows:
- Therefore:
- In the Manning formula, C is not a constant, but a function of R.
- This implies that while C is not a constant, n is a constant.
- However, n has been shown to vary in natural channels, with stage and discharge.
- In natural rivers, n varies as a function of the flow regime: lower, transitional, or upper regime.
- Lower regime has ripples and dunes, which are absent in upper regime.
- Lower regime has skin and form friction; upper regime is mostly skin friction.
|
5.7 DETERMINATION OF MANNING ROUGHNESS
|
- There is no exact method for selecting Manning roughness.
- Recommendations:
- Understand the factors that affect the value of n.
- Consult a table of typical values.
- Chow (B&W photos): minimum n = 0.008; maximum n = 0.250.
- Barnes (color photos): minimum n = 0.024; maximum n = 0.075.
- manningsn.sdsu.edu: minimum n = 0.024; maximum n = 0.075.
- manningsn2.sdsu.edu: minimum n = 0.1; maximum n = 0.2.
- Become acquainted with the appearance of typical channels whose n values are known.
Ash Creek, New Harmony, Utah
Rachichuela Wash, Lambayeque, Peru
- Use theoretical velocity distributions.
- Measure roughness directly (expensive, and stage-dependent).
Streamgaging station at Campo Creek, San Diego County.
|
5.8 FACTORS AFFECTING MANNING'S ROUGHNESS COEFFICIENT
|
-
The value of n is highly variable and depends on a number of factors.
- A. Surface rougness
Fine grains result in a generally low value of n; coarse grains in a high value of n.
- B. Vegetation
Vegetation retards the flow. Maintenance of the channel determines the value of n.
Small depths require higher n. Minimum n = 0.04 for drainage ditches cleared annually.
Use n = 0.05 if clearance is every two years.
Values greater than n = 0.1 may be warranted when channels are not cleared for several years.
Values up to n = 1 may be warranted for flow over vegetation.
Santa Cruz river, near Tucson, Arizona, 1942 and 1989.
- C. Channel irregularities
Tocmoche Canyon, Cajamarca, Peru.
- D. Channel alignment
Meta river, Meta, Colombia.
- E. Silting and scouring
Silting decreases n; scouring increases n.
Uneven deposits such as sand bars and sand waves are channel irregularities and will increase the roughness.
Pirai river, Santa Cruz de la Sierra, Bolivia.
- F. Obstructions
The presence of log jams and bridge piers tend to increase n.
Santo Domingo river, Pernambuco,Brazil.
- G. Size and shape of channel
An increase in hydraulic radius may increase or decrease n, depending on the condition of the channel.
There is no correlation between n and size and shape of channel.
Paraguay river at Porto Murtinho, Mato Grosso do Sul, Brazil.
- H. Stage and discharge
- I. Seasonal change
n increases in the growing season and decreases in the dormant season.
- J. Suspended material and bedload
Suspended material and bedload consume energy and cause an increase in the apparent channel roughness.
Debris flow, foot of the Wasatch Mountains, Utah.
- Procedure for estimating the value of n:
|
n = (n0 + n1 + n2 + n3 + n4) m5
|
- n0 = basic n value for a straight, uniform, smooth channel
- n1 = value added to account for surface irregularities
- n2 = value added to account for variations in the shape and size of the cross section
- n3 = value added to account for obstructions
- n4 = value added to account for vegetation and flow conditions
- m5 = correction factor for channel meandering.

Table 5-5 (Chow)
|
|
Go to Chapter 6.
|













