|
Sy/Sc = [(So/Sc) - F2] / (1 - F2)
Both numerator and denominator are positive -----> subnormal/subcritical flow -----> RETARDED FLOW.
A. Numerator is positive and denominator is negative -----> subnormal/supercritical flow -----> ACCELERATED FLOW.
B. Numerator is negative and denominator is positive -----> supernormal/subcritical flow -----> ACCELERATED FLOW.
Both numerator and denominator are negative -----> supernormal/supercritical flow -----> RETARDED FLOW.
1 > F2 < (So/Sc)
which is the same as:
(So/Sc) > < 1
(So/Sc can be greater, equal to, or less than 1)
(So/Sc) > F2 > 0
Therefore:
So > 0
1 < F2 < (So/Sc)
which is the same as:
(So/Sc) > 1
(So/Sc can only be greater than 1)
(So/Sc) > F2 > 0
Therefore:
So > 0
1 > F2 > (So/Sc)
which is the same as:
(So/Sc) < 1
(So/Sc can only be less than 1)
1 < F2 > (So/Sc)
which is the same as:
(So/Sc) >< 1
(So/Sc can be greater, equal to, or less than 1)
dy/dx = (So - Sc F2) / (1 - F2)
Sy = (So - Sc F2) / (1 - F2)
Sy (1 - F2) = So - Sc F2
Sy - Sy F2 = So - Sc F2
F2 = (So - Sy) / (Sc - Sy)
So = Sc F2
F2 = (So - Sy) / (Sc - Sy)
The following inequality is satisfied: So > Sy < Sc
The following inequality is satisfied: So < Sy > Sc
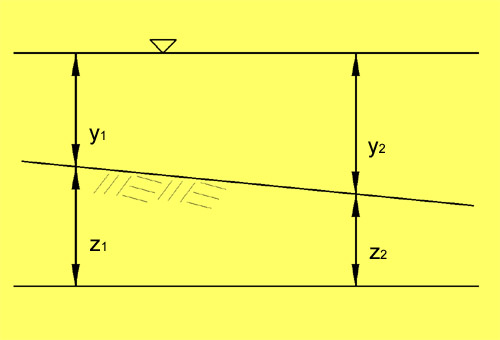
So = (z1 - z2)/L
Sy = (y2 - y1)/L
(z1 - z2)/L = (y2 - y1)/L
z1 + y1 = y2 + z2
The following inequality is NOT satisfied: So > Sy > Sc
The following inequality is NOT satisfied: So < Sy < Sc
We conclude that Sy cannot be less than one and greater than the other slope (So and/or Sc).
Sy has to be either less than both So and Sc, or greater than both (see Case I).
Leads to: So < Sc subcritical flow
Leads to: So = Sc critical flow
Leads to: So > Sc supercritical flow
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
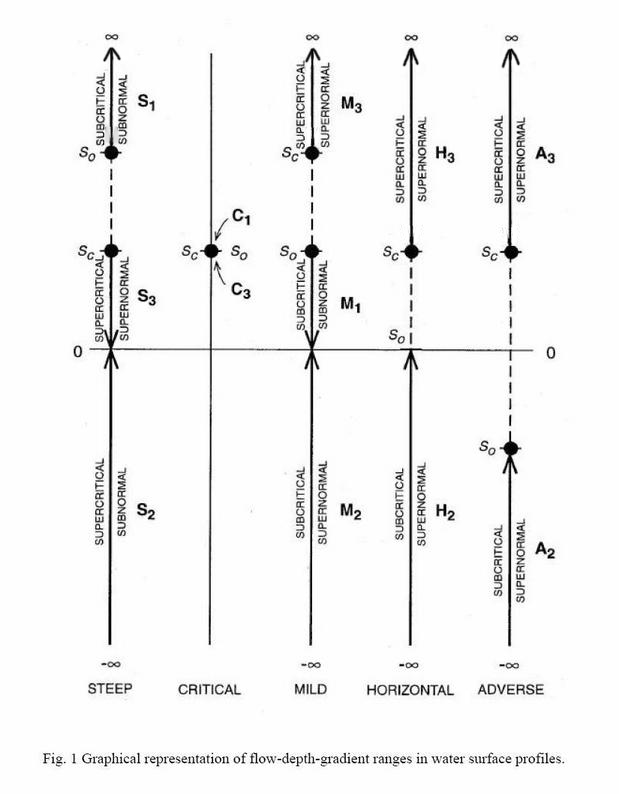
| Table 2. Behavior of depth gradient Sy. | |||
| Channel slope | RETARDED (BACKWATER), Sy is positive, decreasing in the direction of computation | Type | Name |
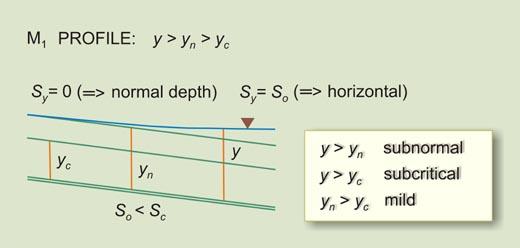
| So < Sc | Sy will decrease U/S from So (Horizontal) to 0 (Asymptotic to flow) | I | M1 |
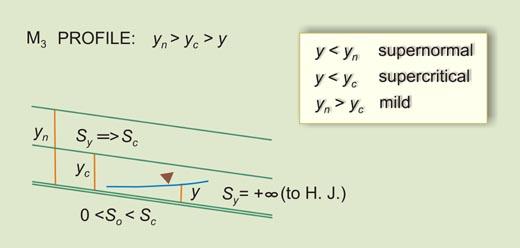
| So < Sc | Sy will increase D/S from Sc (More than horizontal) to +∞ (Vertical) | III | M3 |
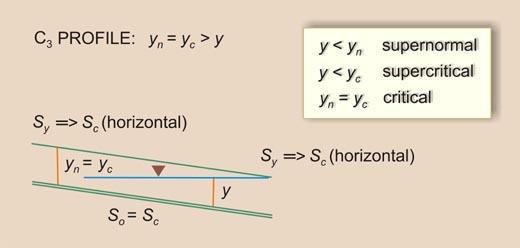
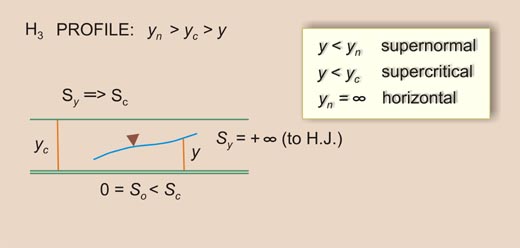
| So < Sc | Sy will increase D/S from Sc (More than horizontal) to +∞ (Vertical) | III | H3 |
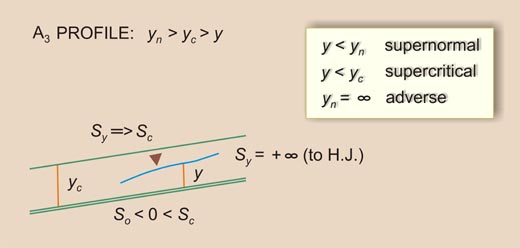
| So < Sc | Sy will increase D/S from Sc (More than horizontal) to +∞ (Vertical) | III | A3 |
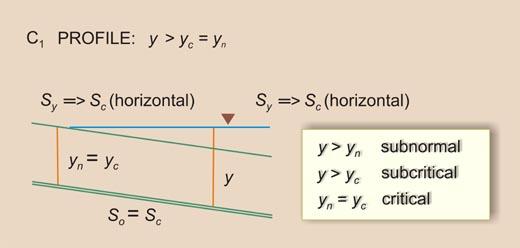
| So = Sc | Sy will be constant and equal to So = Sc | I | C1 |
| So = Sc | Sy will be constant and equal to So = Sc | III | C3 |
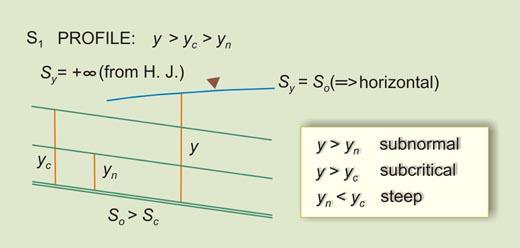
| So > Sc | Sy will increase U/S from So (Horizontal) to +∞ (Vertical) | I | S1 |
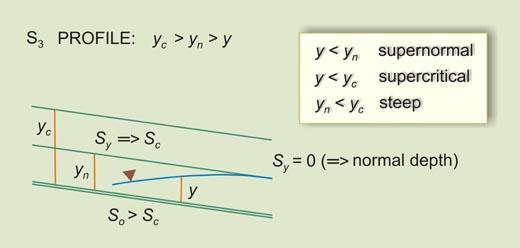
| So > Sc | Sy will decrease D/S from Sc (Less than horizontal) to 0 (Asymptotic to flow) | III | S3 |
| Channel slope | ACCELERATED (DRAWDOWN), Sy is NEGATIVE, increasing in the direction of computation | Type | Name |
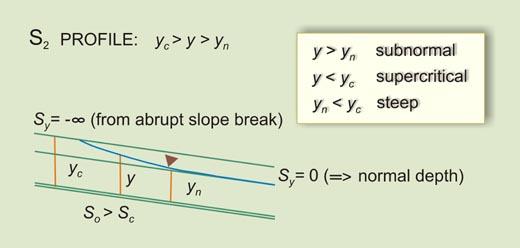
| So > Sc | Sy will increase D/S from -∞ (Vertical) to 0 (Asymptotic to flow) | IIA | S2 |
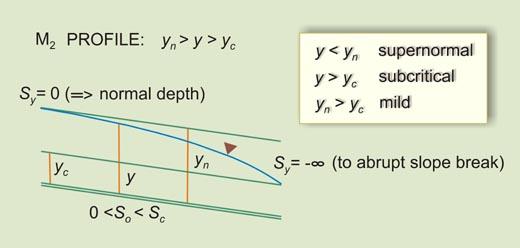
| So < Sc | Sy will increase U/S from -∞ (Vertical) to 0 (Asymptotic to flow) | IIB | M2 |
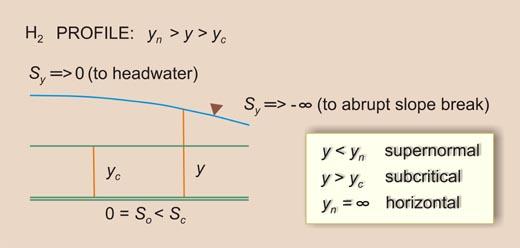
| So < Sc | Sy will increase U/S from -∞ (Vertical) to So = 0 (Asymptotic to flow) | IIB | H2 |
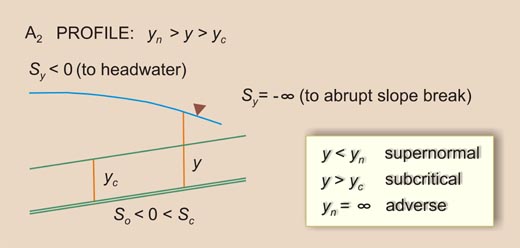
| So < Sc | Sy will increase U/S from -∞ (Vertical) to So < 0 (Asymptotic to flow) | IIB | A2 |
|
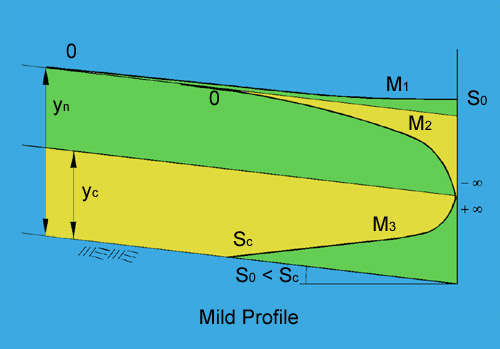
Mild water-surface profiles. |
| Table 3. (a) Occurrence of Water Surface Profiles: Mild channels | ||
| M1 | Flow in a mild channel upstream of a reservoir | |
| M2 | Flow in a mild channel, upstream of an abrupt change in grade (or a steep channel carrying supercritical flow) | |
| M3 | Flow in a mild channel, downstream of a steep channel carrying supercritical flow | |
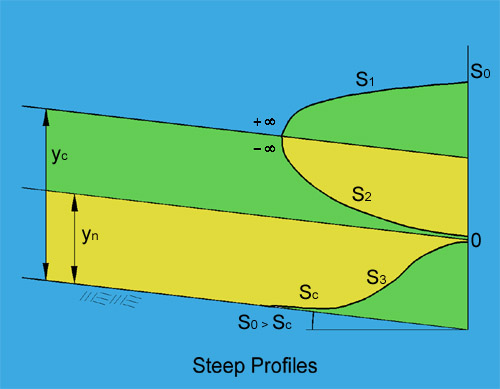
Steep water-surface profiles. |
| Table 3. (b) Occurrence of Water Surface Profiles: Steep channels | ||
| S1 | Flow in a steep channel upstream of a reservoir | |
| S2 | Flow in a steep channel, downstream of a mild channel carrying subcritical flow | |
| S3 | Flow in a steep channel, downstream of a steep channel carrying supercritical flow | |
There are two methods to calculate water-surface profiles:
The number or required cross sections depends on:
Go to Chapter 8C. | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|