CIVE 445 - ENGINEERING HYDROLOGY
CHAPTER 2D: BASIC HYDROLOGIC PRINCIPLES, RUNOFF

Surface runoff, or simply runoff, refers to all waters flowing on the surface of the earth, in:

Overland flow
Rill flow
Gully flow
Streamflow
River flow

Rivers carry their flow into the ocean, completing the hydrologic cycle.
Runoff is expressed in terms of volume or flow rate.
The local flow rate can be integrated over a period of time to give the accumulated runoff volume.
Runoff is commonly expressed in depth units, i.e., the runoff volume spread uniformly over the catchment area.
Runoff is also expressed as:

peak flow per unit drainage area,
peak flow per unit area per unit rainfall intensity (C),
peak flow per unit runoff depth, or
peak flow per unit drainage area per unit runoff depth.

Runoff components

Runoff has three sources:

surface,
interflow,
groundwater.

Surface flow is also called direct runoff.
Direct runoff can produce large flow concentrations in a relatively short period of time.
Direct runoff is responsible for floods.
Interflow is mostly vertical movement of water in the unsaturated portion of the soil profile.
Groundwater flow takes place below the water table.
Groundwater is a characteristically slow process.
Runoff is always moving from higher to lower potential.
Because water table is almost horizontal, groundwater flow is almost horizontal.
Groundwater flow intercepts surface flow in streams and rivers.
Most groundwater flow is converted to surface runoff before it reaches the ocean.
Only about 2% of the water in the hydrologic cycle is unaccounted for as either evaporation or surface runoff.
This unaccounted portion is referred to as deep percolation, and is commonly neglected in water balance studies.

Stream types and baseflow

Streams can be grouped into three types:

perennial,
ephemeral,
intermittent.

Perennial streams are those that always have flow.
During dry weather, the flow of perennial streams is baseflow, consisting mostly of groundwater flow.
Streams that feed from groundwater are called effluent streams.
Perennial and effluent streams are typical of subhumid and humid regions.

A perennial stream: The Deschutes river, central Oregon.

Ephemeral streams flow only in direct response to precipitation.
Ephemeral streams do not intercept groundwater and have no baseflow.
Ephemeral streams usually contribute to groundwater by seepage through their porous channel beds.
Streams that feed groundwater are called influent streams.
Channel abstractions from influent streams are called channel transmission losses.

Equipment to measure field hydraulic conductivity.

Ephemeral and influent streams are typical of semiarid and arid regions.
Intermittent streams are those that have intermediate properties, behaving as either perennial or ephemeral, depending on the season.

An ephemeral stream: Tecate Creek at El Descanso, Baja California.

Baseflow estimates are important in yield hydrology.
In flood hydrology, knowledge of baseflow is necessary to separate direct and indirect runoff.
Baseflow is a measure of indirect runoff.

Antecedent moisture

Surface runoff depends on antecedent moisture.
The more antecedent moisture, the more surface runoff.
The most widely used method for antecedent moisture is the NRCS, which uses uses the Antecedent Moisture Condition (AMC) to characterize antecedent moisture:

I (dry),
II (average) and
III (wet).

Runoff from I is less than II, and II is less than III.

Rainfall-runoff relations

Rainfall is easier to measure than runoff.
From an engineering standpoint, the quantity of runoff is more important that the quantity of rainfall.
Runoff is assessed through rainfall-runoff relations.
A basic linear model of rainfall-runoff is the following:

Q = b (P - P_a)

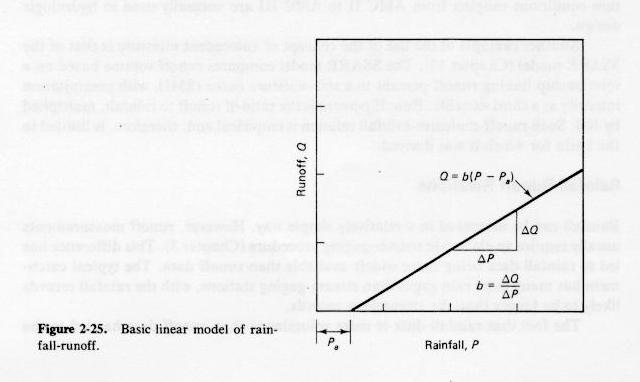
Fig. 2-25

SCS runoff curve number method is a rainfall-runoff model that has a nonlinear fit to the data.
Method is conceptual based on empirical data.

Runoff concentration

Assume that a storm falling on a given catchment produces a uniform effective rainfall intensity over the entire catchment.
In such case, surface runoff will concentrate at the catchment outlet, provided the effective rainfall is sufficiently long.
The flow rate at the outlet increases gradually from zero to a constant maximum, or equilibrium value.
Surface runoff has concentrated at the catchment outlet.
The time to achieve the maximum discharge is referred to as the time of concentration.
The equilibrium flow rate is calculated as follows:

Q_e = 2.78 I_e A

where:

Q_e = equilibrium flow rate, in L/s.
I_e = effective rainfall intensity, in mm/hr.
A = catchment area, in ha.

There are three types of catchment flow:

superconcentrated,
concentrated,
subconcentrated.

Superconcentrated and concentrated flows are typical of small catchments (the rational method).
Subconcentrated flows are typical of midsize (and large) catchments (the unit hydrograph).

Fig. 2-26

Time of concentration

It is the time it takes a parcel of water to travel from the farthest point in the catchment divide to the outlet.
It is a function of runoff rate.
Most formulas for time of concentration are empirical; there are some theoretical (kinematic wave).
The Manning equation is also used to estimate time of concentration.
The speed of travel of unsteady flow is usually larger (by 33% to 67%) than the speed of travel of steady flow.
Time of concentration is essentially unsteady.
Uncertainties in flow rate have blurred the distinction between steady and unsteady velocities in open-channel flow.

The Kirpich formula is the most popular formula for time of concentration:

t_c = 0.06628 L^0.77 / S^0.385

where:

t_c = time of concentration, in hr.
L = catchment length, in km.
S = catchment slope, in m/m.

The Hathaway formula is also popular:

t_c = 0.606 (Ln)^0.467 / S^0.234

where:

n = roughness factor (similar to Manning's).

Runoff diffusion and streamflow hydrographs

Actual catchment response is more complex than that which could be attributed solely to runoff concentration.
Rainfall is not uniformly distributed over space, creating nonuniformities which show as diffusion.
The runoff process is subject to convection and diffusion.
Convection is properly runoff concentration.
Diffusion is the mechanism acting to spread the flows in time and space.
Diffusion reduces the flow levels below those that could be attained by convection only.
Diffusion acts to smooth out catchment response.
The resulting hydrograph is usually continuous.
Typical storm hydrographs are shown below.

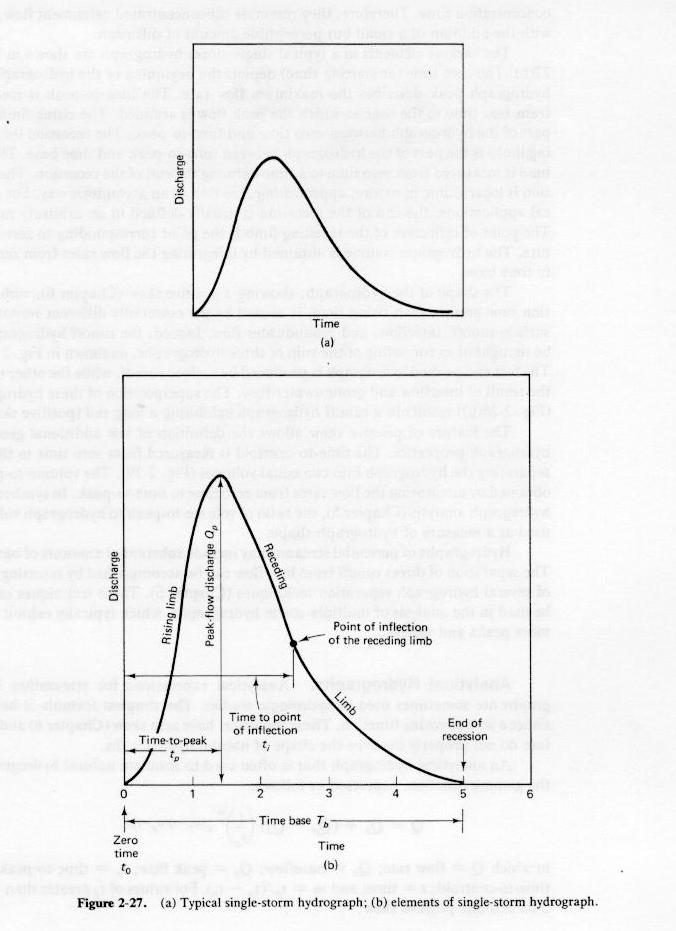
Fig. 2-27

Flow in stream channels

The following properties are used to describe stream channels:

Cross-sectional dimensions: width, depth, area
Cross-sectional shape
Longitudinal slope
Boundary friction

Channel top widths vary widely, from a few meters to several kilometers.
Mean flow depths vary from a fraction of a meter to as high as 60 m for very large rivers such as the Amazon.
Width-to-depth (aspect) ratios vary from about 10 to more than 100.
Water surface slope or energy slope is used as a measure of longitudinal channel slope.
The longer the reach, the more accurate the calculation of channel slope.
Boundary friction can be due to skin or form friction.
Since most rivers have aspect ratios greater than 10, boundary friction is synonymous with bottom friction.

Uniform-flow formulas

The Manning or Chezy formulas are used to calculate uniform flow in stream channels:

The Manning formula is:

V = (1/n) R^2/3 S^1/2

where:

V= mean velocity, m/s.
R= hydraulic radius, m.
S = channel slope, in m/m.

Values of n vary from 0.024 to 0.079 in natural channels (measured by USGS): See manningsn.sdsu.edu
Values of n vary from 0.1 to 0.2 in flood plains: See manningsn2.sdsu.edu

The Chezy formula is also popular:

V = C (RS)^1/2

where:

C = Chezy coefficient, varying from 79 to 11 m^1/2/s.

More typical values of Chezy C are in the range from 40 to 70 m^1/2/s.
Unlike the Manning equation, the Chezy can be made dimensionless by dividing the coefficient by the square root of the gravitational acceleration.
Despite this theoretical appeal, the Manning equation has had wider acceptance in practice.
This is attributed to the fact that the Chezy coefficient has a tendency to vary with the hydraulic radius, such that:

C = (1/n) R^1/6

This implies that Manning's n is a constant.
Experience has shown, however, that n varies with stage and discharge in natural channels.

River stages

At any point, river stage is the elevation of the water surface above a given datum.
River stages vary with flow rate.
Flow rates can be grouped into:

low,
average,
high.

Low flow is typical of the dry season, and consists mostly of baseflow.
High flow occurs during the wet season, and contributions are due primarily to surface runoff.
Average flow occurs in midseason.
The study of low flows is necessary to determine minimum flow rates below which a certain use would be impaired.
Examples:

irrigation water requirements,
hydropower generation,
minimum flows for compliance with water pollution regulations,
minimum draft for inland navigation.

Average flows are used to study catchment yield.
High flows are used to calculate floods, and for flood forecasting and flood control.

Rating curves

Given a long and prismatic channel, a single-valued relationship between stage and discharge at a cross-section defines the equilibrium rating curve.
For steady uniform flow, the rating curve is unique, and can be calculated with a steady flow formula such as Manning's.
The property of uniqueness of the rating qualifies the channel reach as a channel control.
Nonuniformity and unsteadiness can cause deviations from the equilibrium rating curve.
Flood wave theory justifies a loop in the rating.
In practice, the loop is usually small and can be neglected.

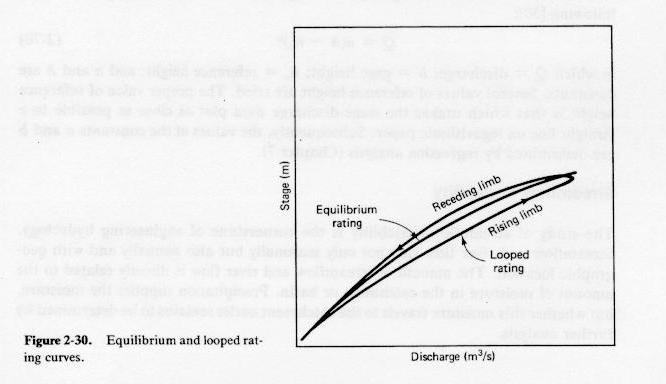
Fig. 2-30

Two other mechanisms have a bearing in the evaluation of stage-discharge relations:

short-term and
long-term

sedimentation effects.
Short-term effect: The amount of boundary friction varies with flow rate.
During low flow, the bed friction consists of grain and form friction.
During high flows, form friction is eliminated, reducing only to grain friction.
The reduced friction gives rivers the capability to carry a greater discharge for a given stage (See Kennedy: Reflections on rivers).
This explains the shift from low-flow rating to high-flow rating.
Long-term sedimentation effect: Rivers continuously subject their boundaries to endless cycles of erosion and deposition, depending on the sediment load they carry.
Shifts in rating curve are the net result of these natural geomorphic processes.

Rating curve formulas

In spite of complexities, rating curves are a useful and practical tool in hydrologic analysis, allowing the direct conversion of stage to discharge and viceversa.
A widely used rating curve model is the following:

Q = a (h - h_o)^b

The proper value of reference stage h_o is that which makes the stage-discharge data plot as close as possible to a straight line on log paper.
Subsequently, values of constants a and b are determined by regression analysis.

Streamflow variability

Streamflow varies seasonally, annually, and with geographic location.
On a global basis, total runoff volume is about 30% of the total precipitation volume.
The rest is accounted for by evaporation and evapotranspiration.
The runoff coefficient could be as low as 2% (Arizona) and as high as 93% (one special case in the Phillipines).

Seasonal variability

In humid climates, seasonal variability is not marked.
The Amazon river has a ratio of high-to-low flow of about 3-5.
In arid climates, seasonal variability is very marked.
Streams in arid climates may have a ratio of high-to-low flow of 1000 or more.
For ephemeral streams, this ratio is ∞ (infinity).
In humid climates, there is contributions of indirect runoff (groundwater flow) throughout the year.
In arid climates, the water table lies deep in the soil profile, and the contribution of groundwater to surface water is absent.
Groundwater reservoirs serve as the mechanism for the storage of large amounts of water, which are slowly transported to lower elevations.
The process is slow and subject to a substantial amount of diffusion.
The net effect is that of a permanent contribution to surface flow in the form of baseflow.

Annual variability

Annual streamflow variability is linked to the relative contributions of direct and indirect runoff.
During dry years, rainfall goes on to replenish the catchment's soil moisture, with little of it showing as direct runoff.
During wet years, the catchment's storage capacity fills up quickly, and any additional amount is entirely converted into surface runoff.
A line of inquiry is to focus on the mechanics of coupled surface and groundwater flow.
This is a very complex process, spatially distributed and temporally varying.
We have relied on statistics to compensate for the incomplete knowledge of the physical processes.
This has led to the concept of flood frequency.
A flood series is extracted from the stream gaging data.
The statistical analysis of the flood series allows the calculation of flow rates associated with selected frequencies or return periods.
The procedure is limited by the record length, i.e., the number of years of data.
With 10 years of data, do not expect to get an accurate value of the 100-yr flood.

Daily flow analysis

Variability of streamflow can be expressed in terms of the day-to-day fluctuation of flow rates at a given station.
Differences are due to the climate and the nature of catchment response.
Small and midsize catchments will usually have steep gradients and concentrate flows with negligible runoff diffusion, producing hydrographs with many high peaks and low valleys.
Large catchments are likely to have milder gradients and therefore, to concentrate flows with substantial runoff diffusion.
The diffusion mechanism acts to spread the flow in time and space, smoothing out the peaks and valleys of the hydrographs.

Flow-duration curve

Daily flow records are obtained for one or more years.
The length of the record indicates the total number of days in the series.
The daily flow series is sequenced in decreasing order, from highest to lowest, and an order number assigned.
For each flow value, the percent time is the ratio of its order number divided by the total number of days, and multiplied by 100.
The flow-duration curve is obtained by plotting flow vs percent time.

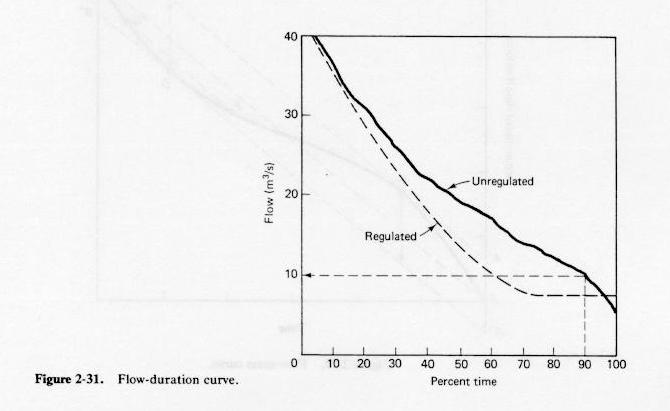
Fig. 2-31

The flow-duration curve allows the evaluation of the permanence of characteristic low-flow levels.
For instance, the flow expected to be exceeded 90% of the time can be readily determined from a flow-duration curve.
The permanence of low flows is increased with streamflow regulation.
The usual aim is to assure the permanence of a certain low-flow level 100% of the time.
Regulation causes a shift in the flow-duration curve by increasing the permanence of low flows while decreasing that of high flows.
Flow-mass curve.

Geographical variability of streamflow

Two variables help describe the geographical variability of streamflow:

catchment area,
mean annual precipitation.

The volume available for runoff is directly proportional to the catchment area.
This is limited by the available precipitation.
Catchment area is important because large catchments have milder overall gradients.
This causes increased runoff diffusion, increasing the chances for infiltration.
The net effect is a decrease of peak discharge per unit area.
Peak flows are directly related to catchment area (Eq. 2-52).

Q_p = c Aⁿ

The exponent n is generally less than 1, because of runoff diffusion.
Therefore, peak flow per unit of catchment area is:

q_p = c / A^m

where m = 1 - n.
This equation confirms that q_p is inversely related to drainage area.
The Creager curves (Fig. 2-33) is an early example of this trend.

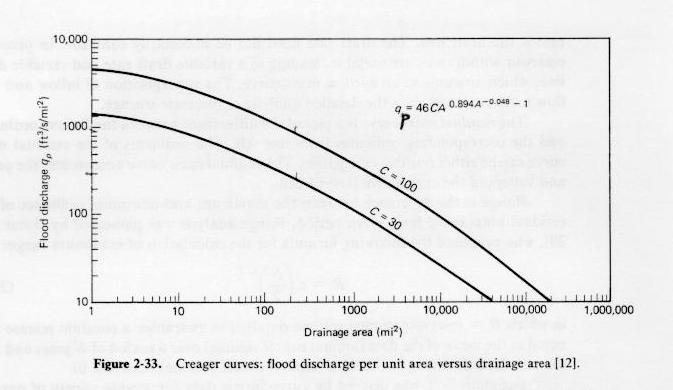
Fig. 2-33

Values of C in the range 30-100 encompass most of the data compiled by Creager in the 1930's.
This range can be taken as a measure of the regional variability of flood discharges.
However, there is no connotation of frequency to the calculated results.

Go to Chapter 3.

100210