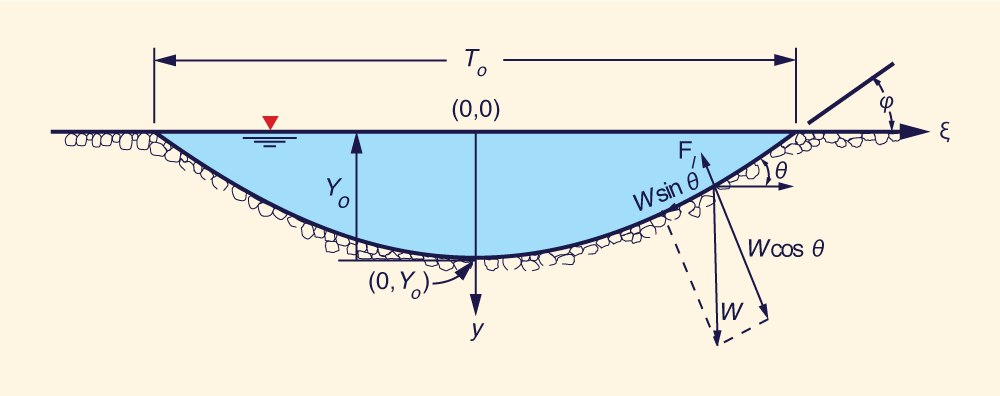
|
THE EQUILIBRIUM SHAPE OF SELF-FORMED CHANNELS
IN NONCOHESIVE ALLUVIUM
Victor M. Ponce and Shurui Jiang
San Diego State University
[201107]
|
Abstract.
The Lane et al. (1959) theory for the equilibrium shape of self-formed
channels in noncohesive alluvium has been revisited, with all assumptions
and derivations clearly stated. The results are used to estimate
self-formed | |||||||||
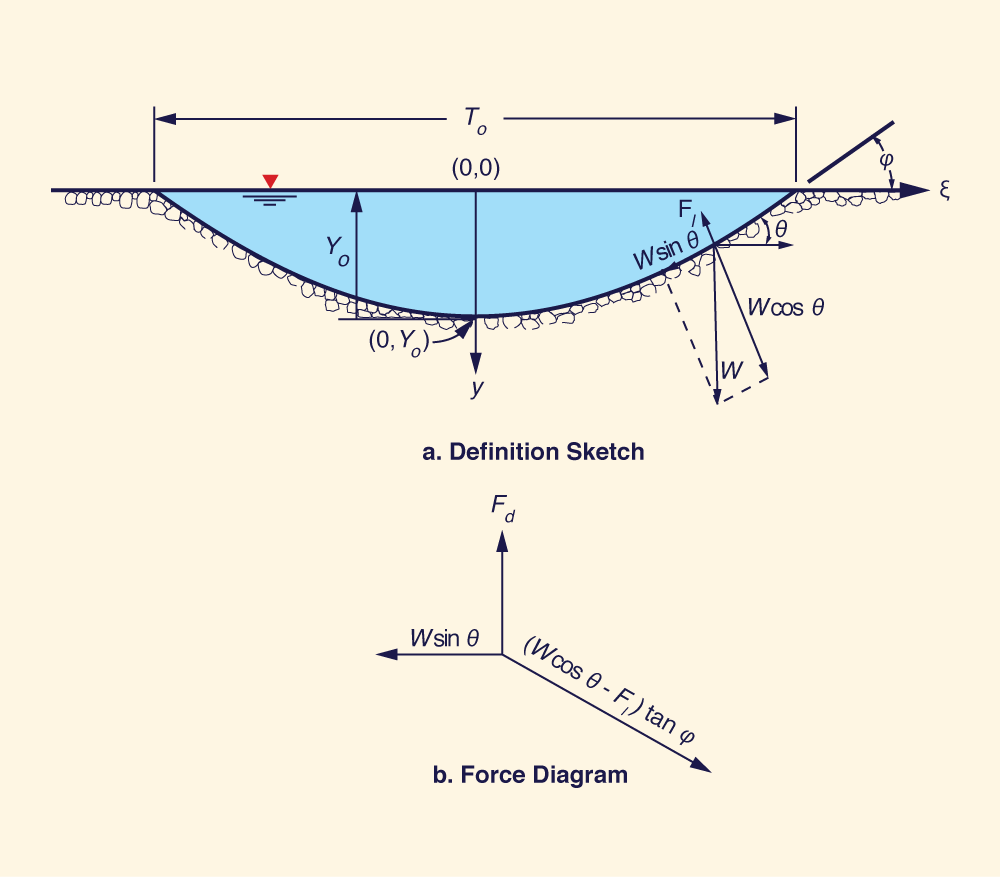
|
3. THE LANE ET AL. METHOD REVISITED
Under the assumption of incipient motion on the periphery of the channel, the drag force Fd, and the downward component
of the submerged weight of the particle, W sinθ, are balanced by the friction force developed between particles. The
angle θ is the local side slope angle and W is the submerged weight of the particle. The friction force is the product
of the normal force and the tangent of the friction angle φ. The normal force is
| W 2 sin2 θ + Fd 2 = [ ( W cos θ - Fl ) tan φ ] 2 | (1) |
It is assumed that Fd = δτ, in which
τ is the local bed shear stress or tractive force and δ is a proportionality constant. Furthermore, it is assumed that
Fl = βFd, where β is
the
| τ 2 + (W/δ)2 sin2 θ = [ (W/δ) cos θ - βτ ] 2 tan2 φ | (2) |
At the channel centerline: θ = 0 and τ = τo (Fig. 1). Substituting this condition into Eq. 2 yields:
| τo2 = [ (W/δ) - βτo ] 2 tan2 φ | (3) |
Solving for W/δ :
|
W 1 + β tan φ ___ = _______________ τo δ tan φ | (4) |
The quantity τo, the tractive force at the channel centerline, is equal to:
| τo = γ Yo S | (5) |
in which γ = unit weight of water, Yo = maximum flow depth, and S = channel bed slope.
At a distance ε from the channel centerline, the depth of flow is y. The weight of fluid in a column of unit area and depth Y
is: γY. The normal component of this fluid weight is:
| τ = γ Y S cosθ | (6) |
Substituting Eq. 5 into Eq. 4 yields:
|
W 1 + β tan φ ___ = _______________ γ Yo S δ tan φ | (7) |
Substituting Eq. 7 into Eq. 2 yields:
|
1 + β tan φ τ 2 + [ ______________ γ Yo S ] 2 sin2 θ = tan φ 1 + β tan φ [ (_______________ γ Yo S ) cos θ - βτ ] 2 tan2 φ tan φ | (8) |
Substituting Eq. 6 into Eq. 8 yields:
|
1 + β tan φ (γ Y S cos θ)2 + [______________ γ Yo S ] 2 sin2 θ = tan φ 1 + β tan φ [ (______________ γ Yo S ) cos θ - β (γ Y S cos θ) ] 2 tan2 φ tan φ | (9) |
Taking the left-hand side (LHS) of this equation and carrying out the squared terms yields:
|
1 + β tan φ γ 2 Y 2 S 2 cos2 θ + ( _____________ ) 2 γ 2 Yo 2 S 2 sin2 θ tan φ | (10) |
Factoring out γ 2 S 2 gives:
|
1 + β tan φ γ 2 S 2 [ Y 2 cos2 θ + ( _____________ ) 2 Yo 2 sin2 θ ] tan φ | (11) |
Working with the right-hand side (RHS) of Eq. 9:
|
1 + β tan φ [ (______________) 2 γ 2 Yo 2 S 2 cos2 θ tan φ 1 + β tan φ - 2 (______________) β γ 2 Y Yo S 2 cos2 θ tan φ + β 2 γ 2 Y 2 S 2 cos2 θ ] tan2 φ | (12) |
Factoring out γ 2 S 2 cos2 θ within the brackets gives:
|
1 + β tan φ γ 2 S 2 cos2 θ [ (______________) 2 Yo 2 tan φ 1 + β tan φ - 2 (______________) β Y Yo + β 2 Y 2 ] tan2 φ tan φ | (13) |
Dividing Eq. 11 (LHS) and Eq. 13 (RHS) by γ 2 S 2 yields:
|
1 + β tan φ Y 2 cos2 θ + (______________) 2 Yo 2 sin2 θ = tan φ 1 + β tan φ 1 + β tan φ cos2 θ [ (______________) 2 Yo 2 - 2 (_____________) β Y Yo tan φ tan φ + β 2 Y 2 ] tan2 φ | (14) |
Dividing Eq. 14 by Yo2 cos2 θ yields:
|
Y 1 + β tan φ (____) 2 + (______________) 2 tan2 θ = Yo tan φ 1 + β tan φ 1 + β tan φ β Y [ (______________) 2 - 2 (______________) _____ tan φ tan φ Yo β Y + (_____) 2 ] tan2 φ Yo | (15) |
from which the following equation is obtained:
|
Y 1 + β tan φ (____) 2 + (____________) 2 tan2 θ = Yo tan φ 1 + β tan φ β Y (____________ - _____) 2 tan2 φ tan φ Yo | (16) |
By definition, tanθ = - dY / dε, and calling r = β tanφ, Eq. 16 can be expressed as follows:
|
Y 1 + r dY 1 + r β Y (____) 2 + (_______) 2 ( - ____ ) 2 = (_______ - _____) 2 tan2 φ Yo tan φ dε tan φ Yo | (17) |
dY
Solving for the expression ( - ____ ) 2 yields:
dε
|
1 + r β Y Y (_______ - _____) 2 tan2 φ - (____) 2 dY tan φ Yo Yo ( - ____ ) 2 = _________________________________________ dε 1 + r ( _______ ) 2 tan φ | (18) |
Working with the right-hand side (RHS) only, carrying out the squared term within the brackets yields:
|
1 + r 1 + r β Y Y Y [ (_______) 2 - 2 (_______) (_____) + β 2 (_____) 2 ] tan2 φ - (_____) 2 tan φ tan φ Yo Yo Yo ____________________________________________________________________
1 + r | (19) |
Simplifying:
|
2 β tan φ Y β 2 tan2 φ Y Y tan2 φ tan2 φ [ 1 - __________ ___ + ___________ (___) 2 ] - (___) 2 _________ ( 1 + r ) Yo ( 1 + r ) 2 Yo Yo ( 1 + r ) 2 | (20) |
Since r = β tan φ, Eq. 20 results in:
|
2 r Y r 2 Y Y tan2 φ tan2 φ [ 1 - ________ ____ + __________ (___) 2 ] - (___) 2 __________ ( 1 + r ) Yo ( 1 + r ) 2 Yo Yo ( 1 + r ) 2 | (21) |
Factoring out tan2 φ gives:
|
2 r Y r 2 Y Y 1 tan2 φ [ 1 - ________ ____ + __________ (___) 2 - (___) 2 _________ ] ( 1 + r ) Yo ( 1 + r ) 2 Yo Yo ( 1 + r ) 2 | (22) |
Simplifying further yields:
|
2 r Y r 2 - 1 Y tan2 φ [ 1 - _________ ____ + ___________ (____) 2 ] ( 1 + r ) Yo ( 1 + r ) 2 Yo | (23) |
Replacing (r 2 - 1) = ( r + 1 )( r - 1 ) yields:
|
2 r Y ( r +1 )( r - 1 ) Y tan2 φ [ 1 - _________ ____ + _______________ (___) 2 ] ( 1 + r ) Yo ( 1 + r ) 2 Yo | (24) |
Simplifying Eq. 24 and substituting into Eq. 18:
|
dY 2 r Y ( r - 1 ) Y ( - ____ ) 2 = tan2 φ [ 1 - ________ ____ + _________ (____) 2 ] dε 1 + r Yo ( 1 + r ) Yo | (25) |
Changing (r - 1) to (1 - r ) gives:
|
dY 2 r Y ( 1 - r ) Y ( - ____ ) 2 = tan2 φ [ 1 - ________ ____ - _________ (____) 2 ] dε 1 + r Yo ( 1 + r ) Yo | (26) |
Taking the square root of each side yields:
|
dY 2 r Y ( 1 - r ) Y ( - ____ ) = tan φ [ 1 - ________ ____ - _________ (____) 2 ] 1/2 dε 1 + r Yo ( 1 + r ) Yo | (27) |
dε
Multiplying each side of the equation by ______ yields:
dYo
|
dY dε 2 r Y ( 1 - r ) Y - ______ = _____ tan φ [ 1 - _______ ____ - _________ (____) 2 ] 1/2 dYo dYo 1 + r Yo ( 1 + r ) Yo | (28) |
Dividing each side by the term within brackets yields:
|
dY / dYo dε ___________________________________________ = - _____ tan φ 2 r Y 1 - r Y dYo [ 1 - (_______) ____ - (_______) (___) 2 ] 1/2 1 + r Yo 1 + r Yo | (29) |
The left-hand side of this equation follows the indefinite integral form:
|
dx 1 2ax + b ∫_______ = - ___________ sin -1 ___________ X 1/2 ( - a ) 1/2 ( - Δ ) 1/2 | (30) |
in which:
| Δ = 4ac - b 2 | (30 a) |
| X = ax 2 + bx + c | (30 b) |
| ( a < 0; Δ < 0 ) | (30 c) |
From Eq. 29, defining:
|
1 - r a = - (_______) 1 + r | (31) |
|
2 r b = - (_______) 1 + r | (32) |
| c = 1 | (33) |
Substituting the terms a, b, and c (Eqs. 31 to 33) in Eq. 30 a yields:
|
1 - r 2 r ( - Δ ) 1/2 = [ - [ 4 ( - ______ ) (1) - ( - ______ ) 2 ] ] 1/2 1 + r 1 + r | (34) |
Carrying out the squared term:
|
1 - r 4 r 2 ( - Δ ) 1/2 = [ - [ 4 ( - ______ ) - ( _________ ) ] ] 1/2 1 + r ( 1 + r ) 2 | (35) |
Simplifying:
|
1 - r 4 r 2 ( - Δ ) 1/2 = [ 4 ( ______ ) + ( _________ ) ] 1/2 1 + r ( 1 + r ) 2 | (36) |
Factoring out a 2 from under the radicand gives:
|
1 - r r 2 ( - Δ ) 1/2 = 2 [ ______ + _________ ] 1/2 1 + r ( 1 + r ) 2 | (37) |
1 + r
Multiplying by (_______) inside the radicand yields:
1 + r
|
( 1 - r 2 ) r 2 ( - Δ ) 1/2 = 2 [ __________ + _________ ] 1/2 ( 1 + r ) 2 ( 1 + r ) 2 | (38) |
Collecting common terms yields:
|
2 ( - Δ ) 1/2 = ______ 1 + r | (39) |
Therefore, in Eq. 30:
|
1 - r Y -2 r [ 2 ( - ( ______ ) ) (____) + ( ______ ) ] dx 1 1 + r Yo 1 + r ∫_______ = - ___________ sin -1 ______________________________________ 1 - r 2 X 1/2 (______) 1/2 ______ 1 + r 1 + r | (40) |
Inverting the square root term in the denominator and simplifying further:
|
dx 1 + r Y ∫_______ = - (______) 1/2 sin -1 [ - ( 1 - r ) ____ - r ] X 1/2 1 - r Yo | (41) |
Integrating the right hand side (RHS) of Eq. 29 gives:
|
ε - ____ tan φ + C Yo | (42) |
Now, equating Eqs. 41 and 42 gives:
|
ε 1 + r Y - ____ tan φ + C = - (______) 1/2 sin -1 [ - ( 1 - r ) ____ - r ] Yo 1 - r Yo | (43) |
The constant of integration is evaluated by recognizing that Y/Yo = 1 for ε/Yo = 0. Therefore:
|
1 + r C = - (______) 1/2 sin -1 ( - 1 ) 1 - r | (44) |
which reduces to:
|
π 1 + r C = (___) (______) 1/2 2 1 - r | (45) |
The substitution of C (Eq. 45) into Eq. 43 yields:
|
ε π 1 + r 1 + r Y - ____ tan φ + ___ (______) 1/2 = - (______) 1/2 sin -1 [ - ( 1 - r ) ____ - r ] Yo 2 1 - r 1 - r Yo | (46) |
1 + r
Dividing by - (_______) 1/2 yields:
1 - r
|
ε π 1 + r - ____ tan φ + ___ (______) 1/2 Yo 2 1 - r Y _______________________________ = sin -1 [ - ( 1 - r ) ____ - r ] 1 + r Yo - (_____) 1/2 1 - r | (47) |
Taking the sine of each side yields:
|
ε π 1 + r - ____ tan φ + ___ (______) 1/2 Yo 2 1 - r Y - sin [ _______________________________ ] = ( 1 - r ) ____ + r 1 + r Yo - (_____) 1/2 1 - r | (48) |
Simplifying the left-hand side:
|
ε 1 - r π Y - sin [ ____ (______) 1/2 tan φ - ___ ] = ( 1 - r ) ____ + r Yo 1 + r 2 Yo | (49) |
Y
Solving for ____ yields:
Yo
|
ε 1 - r π - sin ( ____ (______) 1/2 tan φ - ___ ) - r Y Yo 1 + r 2 ____ = __________________________________________ Yo 1 - r | (50) |
From the trigonometric identity:
|
π sin ( ____ - θ ) = cos θ 2 | (51) |
where θ in this case is:
|
ε 1 - r θ = ____ (______) 1/2 tan φ Yo 1 + r | (52) |
it follows that:
|
ε 1 - r cos ( ____ (______) 1/2 tan φ ) - r Y Yo 1 + r ____ = ____________________________________ Yo 1 - r | (53) |
For Y = 0, ε = To /2, in which To = channel top width. Substituting these values into Eq. 53:
|
To 1 - r cos [ ______ (______) 1/2 tan φ ] - r = 0 2Yo 1 + r | (54) |
Solving for r in Eq. 54:
|
To 1 - r r = cos [ ______ (______) 1/2 tan φ ] 2Yo 1 + r | (55) |
from which:
|
To 1 - r cos-1 r = ______ (______) 1/2 tan φ 2Yo 1 + r | (56) |
from which:
|
To 2
1 + r ______ = _________ (______) 1/2 cos-1 r Yo tan φ 1 - r | (57) |
Equation 57 is the relationship derived by Lane et al. (1959) linking the top-width-to-maximum-depth ratio
(a parameter describing the shape of the cross section) to the values of
For β = 0, i.e., in the absence of lift forces, it follows that r = 0, and Eq. 57 reduces to:
|
To π
______ = _________ Yo tan φ | (58) |
For φ = 45°, this equation (Eq. 58) reduces to:
|
To
______ = π = 3.14 Yo | (59) |
In the limit, as β ⇒ 1 and φ ⇒ 45°, it can be shown that (See Appendix):
|
To
______ ⇒ 4 Yo | (60) |
4. SENSITIVITY ANALYSIS
The sensitivity of Lane et al.'s formula for the shape
of self-formed channels in noncohesive alluvium (Eq. 57)
has been studied by varying the friction angle θ
and the ratio β of lift-to-drag forces between realistic ranges.
The friction angle φ of noncohesive material varies normally
in the range 25°-45°.
Values of β are somewhat more difficult to determine with sufficient accuracy. Apperley's (1968) detailed laboratory study concluded that the mean value of β is a function of elevation above the bed. He plotted y/ds vs. β in which y = elevation, and ds = grain diameter, and showed that β reached a maximum of 0.75 for y/ds = 0.25 (Fig. 2), decreasing to 0 for y/ds = 0.90. Above y/ds = 0.90, the mean lift becomes negative, at least up to y/ds = 1.50.
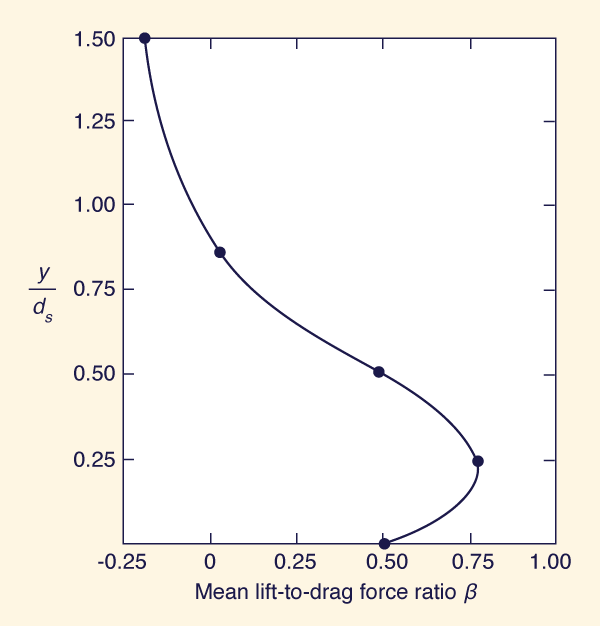
|
Fig. 2 Mean lift-to-drag force ratio β
as a function of normalized
elevation along the bed
y/ds (Apperley, 1968).
Given the experimental evidence of Apperley and others, as discussed thoroughly by the former, it was decided to vary the lift-to-drag ratio in the range -1.0 ≤ β ≤ 1.0. Large negative values of β are not considered likely; they are shown here only for illustrative purposes.
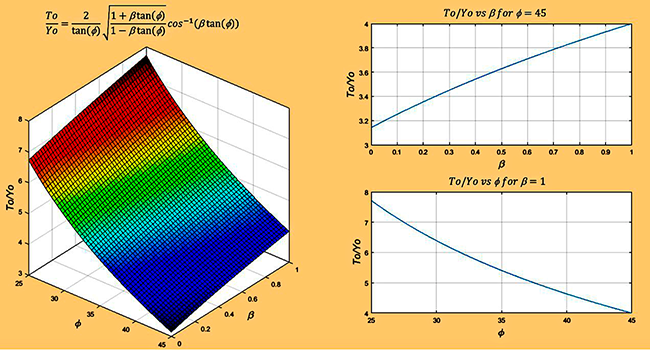
Table 1 shows calculated values of top-width/maximum-depth
(To /Yo) as a function of φ and β, within the indicated parameter ranges.
It is clearly seen that for small values
of φ, say φ ≤ 10°, the presence
of lift does not substantially affect the shape of the
cross section. The converse is true for large values of
φ, say in the
range
| Table 1. Value of To /Yo as a function of friction angle φ and lift-to-drag force ratio β. | |||||||||
| β | Friction angle φ (degrees) | ||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | |
| -1.0 | 34.728 | 16.591 | 10.447 | 7.292 | 5.320 | 3.920 | 2.814 | 1.809 | 0.001 |
| -0.9 | 34.849 | 16.722 | 10.589 | 7.448 | 5.495 | 4.124 | 3.064 | 2.160 | 1.235 |
| -0.8 | 34.970 | 16.851 | 10.728 | 7.598 | 5.660 | 4.310 | 3.284 | 2.438 | 1.665 |
| -0.7 | 35.090 | 16.978 | 10.862 | 7.743 | 5.817 | 4.484 | 3.480 | 2.672 | 1.971 |
| -0.6 | 35.210 | 17.103 | 10.994 | 7.882 | 5.966 | 4.645 | 3.658 | 2.874 | 2.214 |
| -0.5 | 35.328 | 17.226 | 11.123 | 8.017 | 6.109 | 4.796 | 3.822 | 3.054 | 2.418 |
| -0.4 | 35.446 | 17.348 | 11.248 | 8.148 | 6.245 | 4.939 | 3.973 | 3.216 | 2.595 |
| -0.3 | 35.563 | 17.467 | 11.371 | 8.274 | 6.375 | 5.074 | 4.113 | 3.364 | 2.752 |
| -0.2 | 35.679 | 17.585 | 11.492 | 8.397 | 6.500 | 5.202 | 4.245 | 3.500 | 2.894 |
| -0.1 | 35.794 | 17.702 | 11.609 | 8.516 | 6.621 | 5.325 | 4.369 | 3.626 | 3.023 |
| 0.0 | 35.909 | 17.817 | 11.725 | 8.631 | 6.737 | 5.441 | 4.487 | 3.744 | 3.142 |
| 0.1 | 36.022 | 17.930 | 11.838 | 8.744 | 6,849 | 5.553 | 4.598 | 3.855 | 3.252 |
| 0.2 | 36.135 | 18.042 | 11.948 | 8.854 | 6.958 | 5.660 | 4.704 | 3.959 | 3.354 |
| 0.3 | 36.248 | 18.153 | 12.057 | 8.961 | 7.063 | 5.763 | 4.805 | 4.058 | 3.451 |
| 0.4 | 36.359 | 18.262 | 12.164 | 9.065 | 7.165 | 5.863 | 4.902 | 4.152 | 3.542 |
| 0.5 | 36.470 | 18.370 | 12.269 | 9.167 | 7.264 | 5.959 | 4.994 | 4.241 | 3.628 |
| 0.6 | 36.580 | 18.476 | 12.371 | 9.266 | 7.360 | 6.051 | 5.083 | 4.327 | 3.709 |
| 0.7 | 36.690 | 18.581 | 12.473 | 9.363 | 7.453 | 6.141 | 5.169 | 4.408 | 3.787 |
| 0.8 | 36.799 | 18.685 | 12.572 | 9.458 | 7.544 | 6.227 | 5.252 | 4.487 | 3.861 |
| 0.9 | 36.907 | 18.788 | 12.670 | 9.551 | 7.632 | 6.311 | 5.331 | 4.562 | 3.932 |
| 1.0 | 37.014 | 18.889 | 12.766 | 9.642 | 7.718 | 6.393 | 5.408 | 4.635 | 4.000 |
Based on Apperley's study, the average value of β integrated along a depth equal to the particle size could be taken as approximately β = 0.4. Values of To /Yo rounded to two decimal places, for β = 0.4 and 25° ≤ φ ≤ 45°, are given in Table 2. These values may be taken as typical equilibrium values for the indicated friction angles.
|
Table 2. Value of To /Yo as a
function of friction angle φ for lift-to-drag ratio β = 0.4. | |||||||||
| φ (degrees) | Top-width to maximum-depth ratio To /Yo | ||||||||
| 25 | 7.16 | ||||||||
| 30 | 5.86 | ||||||||
| 35 | 4.90 | ||||||||
| 40 | 4.15 | ||||||||
| 45 | 3.54 | ||||||||
5. ONLINE CALCULATION
Equation 57 may be solved with the aid of the online calculator
ONLINE LANE SHAPE.
For instance, for Yo = 1 m, φ = 30°, and β = 0.4,
the answer is:
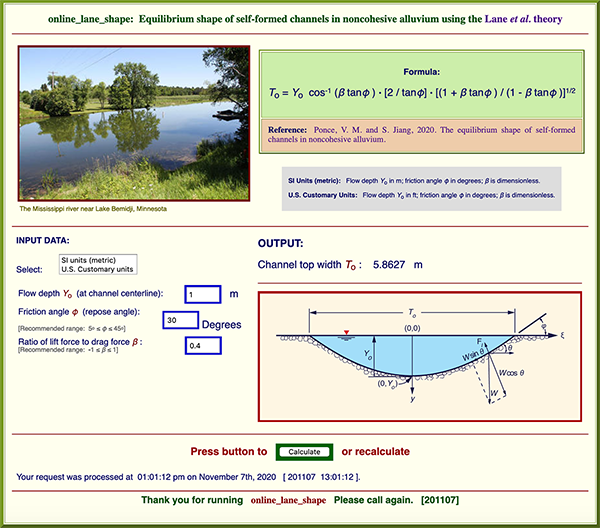
6. CONCLUDING REMARKS
The Lane et al. (1959) theory for the equilibrium shape
of self-formed channels in noncohesive alluvium
has been revisited, with all assumptions and derivations
clearly stated. The results are used to estimate
top-width/maximum-depth cross-sectional ratios as a function of: (1) the
friction angle of the noncohesive
material forming the channel bed, and (2) the
APPENDIX
By Jhonath Wensenber Mejia Gonzales
L'Hospital's rule analysis to show that the top-width/maximum-depth ratio
To /Yo
(Eq. 57)
|
Equation 57 of the main body of this article is:
|
To 2
1 + r ______ = _________ (______) 1/2 cos-1 r Yo tan φ 1 - r | (57) |
The limit of the value of To /Yo for β = 1 and φ = π /4 is:
|
To 2
1 + β tan φ lim [ lim ( ___ ) ] = lim [ lim [ (______) [ (____________) ] 1/2 cos-1(β tan φ) ] ] β↠1 φ↠π /4 Yo β↠1 φ↠π /4 tan φ 1 - β tan φ | (A.1) |
Applying the limit for β ↠ 1 :
|
To 2
1 + (1) tan φ lim [ lim ( ___ ) ] = lim [ (______) [ (_____________) ] 1/2 cos-1((1) tan φ) ] β↠1 φ↠π /4 Yo φ↠π /4 tan φ 1 - (1) tan φ | (A.2) |
|
To 2 1 + tan φ lim [ lim ( ___ ) ] = lim [ (______) [ (___________) ] 1/2 cos-1( tan φ ) ] β↠1 φ↠π /4 Yo φ↠π /4 tan φ 1 - tan φ | (A.3) |
|
To
(1 + tan φ) 1/2 cos-1( tan φ ) lim [ lim ( ___ ) ] = 2 lim [ (_____________________________) ] β↠1 φ↠π /4 Yo φ↠π /4 tan φ (1 - tan φ) 1/2 | (A.4) |
The expression (1 + tan φ)1/2 = (2)1/2 is taken out of the limit because the indeterminate term "0/0" does not depend on (1 + tan φ)1/2. Therefore:
|
To
cos-1 ( tan φ ) lim [ lim ( ___ ) ] = 2 (2)1/2 lim [ (_______________________) ] β↠1 φ↠π /4 Yo φ↠π /4 tan φ (1 - tan φ) 1/2 | (A.5) |
Applying L'Hospital's rule:
|
d ____ [ cos-1 ( tan φ ) ] To dφ lim [ lim ( ___ ) ] = 2 (2)1/2 lim _______________________________ β↠1 φ↠π /4 Yo φ↠π /4 d ____ [ tan φ (1 - tan φ) 1/2 ] dφ | (A.6) |
|
sec2 φ - _______________ To (1 - tan2 φ) 1/2 lim [ lim ( ___ ) ] = 2 (2)1/2 lim [ _________________________________________ ] β↠1 φ↠π /4 Yo φ↠π /4 tan φ sec2 φ sec2 φ (1 - tan φ) 1/2 - _________________ 2 (1 - tan φ) 1/2 | (A.7) |
|
1 - _______________ To (1 - tan2 φ) 1/2 lim [ lim ( ___ ) ] = 2 (2)1/2 lim [ _________________________________ ] β↠1 φ↠π /4 Yo φ↠π /4 tan φ (1 - tan φ) 1/2 - _________________ 2 (1 - tan φ) 1/2 | (A.8) |
|
1 - _______________ To (1 - tan2 φ) 1/2 lim [ lim ( ___ ) ] = 2 (2)1/2 lim [ ________________________ ] β↠1 φ↠π /4 Yo φ↠π /4 2 (1 - tan φ) - tan φ ____________________ 2 (1 - tan φ) 1/2 | (A.9) |
|
1 - _______________ To (1 - tan2 φ) 1/2 lim [ lim ( ___ ) ] = 2 (2)1/2 lim [ ________________________ ] β↠1 φ↠π /4 Yo φ↠π /4 2 - 3 tan φ __________________ 2 (1 - tan φ) 1/2 | (A.10) |
|
1 - ____________________________ To (1 + tan φ) 1/2 (1 - tan φ) 1/2 lim [ lim ( ___ ) ] = 2 (2)1/2 lim [ ___________________________________ ] β↠1 φ↠π /4 Yo φ↠π /4 2 - 3 tan φ __________________ 2 (1 - tan φ) 1/2 | (A.11) |
|
1 - ______________ To (1 + tan φ) 1/2 lim [ lim ( ___ ) ] = 2 (2)1/2 lim [ ____________________ ] β↠1 φ↠π /4 Yo φ↠π /4 2 - 3 tan φ _______________ 2 | (A.12) |
Substituting φ = π / 4:
|
1 - ___________________ To [ 1 + tan(π / 4) ] 1/2 lim [ lim ( ___ ) ] = 2 (2)1/2 [ ________________________ ] β↠1 φ↠π /4 Yo 2 - 3 tan(π / 4) ________________ 2 | (A.13) |
|
1 - ___________ To (1 + 1) 1/2 lim [ lim ( ___ ) ] = 2 (2)1/2 [ _______________ ] β↠1 φ↠π /4 Yo 2 - 3 ______ 2 | (A.14) |
|
To 2 lim [ lim ( ___ ) ] = 2 (2)1/2 [ _______ ] β↠1 φ↠π /4 Yo 2 1/2 | (A.15) |
|
To lim [ lim ( ___ ) ] = 4 β↠1 φ↠π /4 Yo | (A.16) |
Therefore, it is proven that To / Yo = 4 when β = 1 and φ = π / 4.
PDF file
REFERENCES
Apperley, L. W. 1968. The effect of turbulence
on sediment entrainment. Thesis submitted
to the School of Engineering, University of
Auckland, Auckland, New Zealand, in partial fulfillment for the
requirements for the degree
of Doctor of Philosophy, January.
Lane, E. W., P. N. Lin, and H. K. Liu. 1959.
The most efficient stable channel for comparatively
clean water in noncohesive material.
Report CER-59HKL,
Colorado State University, Fort Collins, Colorado,
April.
NOTATION
a = variable, Eqs. 30 and 31;
b = variable, Eqs. 30 and 32;
C = constant of integration;
c = variable, Eqs. 30 and 33;
ds = grain diameter;
Fd = drag force;
Fl = lift force;
r = β tan φ;
S = slope of channel bed;
To = channel top width;
W = particle weight;
X = generic variable, Eq. 30;
Y = flow depth at abscissa ε (Fig. 1);
Yo = flow depth at channel centerline (maximum flow depth);
β = ratio of lift-to-drag forces acting on a particle;
γ = unit weight of water;
Δ = variable, in Eq. 30;
δ = proportionality constant, Fd = δτ;
ε = abscissa of flow depth Y (Fig. 1);
θ = local side slope angle (Fig. 1);
π = 3.1416;
τ = shear stress;
τo = shear stress at channel centerline (maximum shear stress); and
φ = friction angle, repose angle.
ABOUT THE AUTHORS
Victor M. Ponce
and Shurui Jiang are
emeritus professor and M.S. graduate, respectively,
at the department of civil engineering at San Diego State University,
San Diego, California, USA.


Jhonath W. Mejia Gonzales
is a hydraulic engineer
residing in Cajamarca, Peru.

| 201117 13:30 |