|
Inundación en el Río Chané, departamento de Santa Cruz, Bolivia (15 de Enero de 1990). EL NÚMERO DE COURANT
Profesor Emérito de Ingeniería Civil y Ambiental
Universidad Estatal de San Diego, San Diego,
California
1. INTRODUCCIÓN
El número de Courant es un concepto fundamental en el campo de la
dinámica de fluidos computacional (DFC) y, por extensión, de la
hidráulica computacional. El número conecta efectivamente las propiedades
físicas y numéricas de un esquema dado, con aplicación
específica al problema de convección, es decir,
El nombre Courant reconoce la obra de Richard Courant,
renombrado matemático alemán-estadounidense y
uno de los más tempranos contribuyentes al campo de las
matemáticas aplicadas. El concepto de número de
Courant tiene sus raíces en la condición de
Courant-Friedrichs-Lewy, la cual se conoce ampliamente
como condición CFL
En este artículo realizamos un análisis del número de Courant, arrojando nueva
luz sobre su comportamiento. Nos centramos específicamente
en la solución numérica del problema de convección,
revelando propiedades que pueden haber estado
ocultas hasta ahora en aplicaciones convencionales
de la dinámica de fluidos e hidráulica computacional.
2. EL PROBLEMA DE
CONVECCIÓN Y EL ESQUEMA GENERAL DE CUATRO PUNTOS
Comenzamos por conceptualizar el problema de convección
de la mecánica de fluidos. Una cantidad física ζ
se moverá, en el espacio x y en el tiempo t,
con una cierta velocidad convectiva u siguiendo
la ecuación diferencial parcial de primer orden
(Ponce et al., 1979):
Esta ecuación se puede resolver numéricamente de varias maneras.
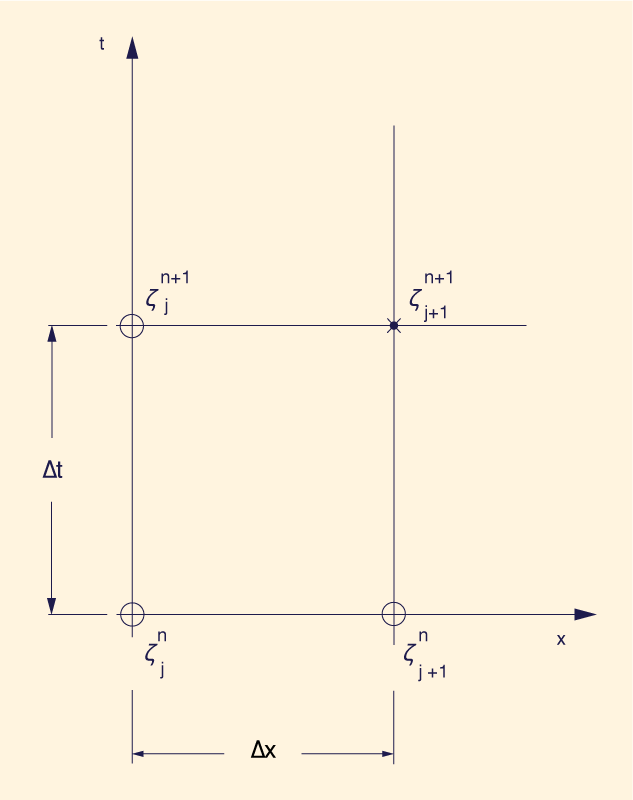
Una formulación lineal explícita de diferencias finitas está
representada por
el siguiente esquema (Fig. 1):
En la Ecuación 2, resolviendo para el valor no conocido ζ j+1 n+1:
Los coeficientes se definen como sigue:
en los cuales el numero de Courant C se define como sigue:
Dado un número de Courant, habiéndose establecido previamente los factores de ponderación X e Y, y utilizando las Ecs. 2 a 7, el cálculo procede a calcular los valores de ζ para todos y cada uno de los puntos de la malla.
La Ecuación 3, junto con las Ecuaciones 4 a 7, constituye
una familia de esquemas numéricos de la ecuación de convección,
Ec. 1. Sus propiedades de estabilidad y convergencia dependen
de los valores de X, Y, y C.
Los dos primeros, denominados factores
de ponderación, y C, el número de Courant, caracterizan el esquema elegido. Reiterando, el número de Courant
es la relación entre la velocidad convectiva u y la relación
de la malla, o "velocidad de la malla"
3. DIFUSIÓN Y DISPERSIÓN NUMÉRICA
La Ecuación 1 describe la convección, un proceso de primer orden;
por lo tanto, no tiene en cuenta la difusividad, un proceso de segundo orden,
y la dispersividad, un proceso de tercer orden (Ponce, 2023).
Una medida de la cantidad de difusión y dispersión numéricas se puede obtener a partir
del error de aproximación del esquema de diferencias finitas, la Ec. 2. Este error
se obtiene expandiendo la función de la malla ζ(jΔx, nΔt)
en serie de Taylor
alrededor del punto (jΔx, nΔt),
lo cual lleva a lo siguiente (Cunge, 1969;
Ponce et al., 1979):
en la cual R = el error de aproximación. De la Ec. 8, observamos que para X = Y = 1/2,
el esquema tiene una precisión de segundo orden. es decir, R = ο(Δx2).
Además, para C = 1, la precisión es de tercer orden; es decir,
la dispersión numérica desaparece. De hecho, para X = Y = 1/2 y C = 1
se obtiene la solución exacta de la ecuación de convección (Ec. 1).
En la Ecuación 8, el coeficiente del término de segundo orden ∂2ζ /∂x2 se denomina coeficiente de difusión numérica y se define de la siguiente manera:
Los valores positivos de μn hacen que el esquema se difusione
numéricamente; los valores negativos amplifican numéricamente.
Mientras que en el primer caso la convergencia se ve perjudicada,
en el segundo la estabilidad se ve afectada. Tanto la estabilidad
como la convergencia mejoran cuando
I. Esquema hacia adelante en el tiempo y hacia atrás en el espacio.
II. Esquema hacia adelante en el espacio y hacia atrás en el tiempo.
III. Esquema hacia atrás en el espacio y hacia atrás en el tiempo.
El presente artículo permite llegar a las siguientes conclusiones:
Al contrario de los esquemas explícitos, los esquemas implícitos se han visto favorecidos debido a sus percibidas mejores propiedades de estabilidad, supuestamente presentando lo que a menudo se ha denominado "estabilidad incondicional". La experiencia, sin embargo, demuestra lo contrario. En general, tanto los esquemas numéricos explícitos como los implícitos están sujetos a situaciones (condiciones) de estabilidad y convergencia. Se recomienda un análisis de von Neumann para mejorar la práctica de la modelación numérica (Ponce et al., 1978).
4. RESUMEN
En este artículo detallamos el papel del número de Courant en la
hidráulica computacional, particularmente en el modelado del problema
de convección pura. Arrojamos una luz renovada sobre las propiedades
de estabilidad y convergencia de una clase de esquemas numéricos
lineales explícitos de la ecuación de convección pura.
Se ha demostrado que tanto la estabilidad condicional como la
incondicional son posibles con esquemas explícitos. Además, se ha
demostrado que la existencia de difusión numérica, atribuible
a los errores de primer orden del esquema numérico,
afecta el cálculo, haciendo que la solución dependa del tamaño de la
malla y sea claramente difusiva para todos los
casos distintos del número de Courant C = 1.
REFERENCIAS
Courant, R., K. Friedrichs, Y H. Lewy. 1928.
Über die partiellen Differenzengleichungen der mathematischen Physik,
Mathematische Annalen, vol. 100, p. 32-74.
Cunge, J. A. 1969.
On the Subject of a Flood Propagation Computation Method (Muskingum Method).
Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.
Ponce, V. M., H. Indlekofer, y D. B. Simons. 1978.
Convergence of four-point implicit water wave models.
Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY7,
July, 947-958.
Ponce, V. M., Y. H. Chen, y D. B. Simons. 1979.
Unconditional stability in convection computations. Journal of the Hydraulics Division, ASCE, Vol. 105, No. HY9,
September, 1079-1086.
Ponce, V. M. 2014.
Engineering Hydrology: Principles and Practices. Second edition, online.
Ponce, V. M. 2023.
Is dispersion important in flood routing? Online paper.
Ponce, V. M. 2023.
When is the diffusion wave applicable? Online paper.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 240614 |