FROUDE Y VEDERNIKOV: PILARES DE LA HIDRÁULICA DE CANALES
Profesor Emérito de Ingeniería Civil y Ambiental
Universidad Estatal de San Diego,
California
1. INTRODUCCIÓN
A principios del siglo XX, la ingeniería hidráulica, una rama de la ingeniería civil,
comenzó a experimentar un acelerado ritmo de desarrollo. La población mundial estaba
aumentando, y se estaba volviendo claro que las sociedades humanas tenían que
confiar en el en ese entonces novedoso método científico para la utilización y
gestión de los recursos hídricos. A principios del Siglo XX, el uso del número de Froude,
desarrollado en Inglaterra en la década de 1860, se estableció firmemente en la práctica
de la ingeniería hidráulica.
El número de Froude define el umbral en el que la velocidad media del
flujo es igual a la velocidad relativa, es decir,
la celeridad relativa, de una pequeña perturbación superficial.
En este artículo, demostramos que las tres velocidades que definen estos
dos conceptos básicos
2. WILLIAM FROUDE: UNA BREVE BIOGRAFÍA
William Froude fue un distinguido ingeniero de nacionalidad británica, especialista en hidrodinámica y arquitectura naval. Nació en Dartington, en Devon, Inglaterra, el 28 de noviembre de 1810. Falleció de un derrame cerebral a los 69 años durante un crucero a Simon's Town, Sudáfrica. Froude estudió matemáticas en Oxford. En 1832, inmediatamente después de su graduación, trabajó para Isambard Kingdom Brunel, el reconocido impulsor de ferrocarriles, como topógrafo en el Ferrocarril Great Western, en Inglaterra. En 1857, Brunel le consultó sobre el comportamiento del barco Great Eastern en altamar. En base a las recomendaciones de Froude, Brunel modificó el diseño del casco del barco para minimizar la posibilidad de volteo.
A partir de 1859, utilizando sus
propios recursos, Froude construyó el primer tanque de remolque En 1861, Froude escribió un artículo sobre el diseño de la estabilidad de los barcos, publicado en las Actas de la Institución de Arquitectos Navales (Proceedings of the Institution of Naval Architects). Entre 1863 y 1867, demostró la relación existente entre el modelo y el prototipo, afirmando que la resistencia por fricción era igual en ambos cuando la velocidad V era proporcional a la raíz cuadrada de la longitud del barco L. A este concepto Froude denominó la Ley de Comparación:
en la cual k es una constante aplicable tanto al modelo como al prototipo. La Ecuación 1 se conoce como la ley de Froude. Froude fue el primero en identificar la forma más eficiente para el casco de los barcos, así como en predecir la estabilidad de los mismos en base a modelos a escala reducida (Fig. 1). En la hidráulica de canales abiertos, la ley de Froude se expresa como el reconocido número de Froude, definido de la siguiente manera:
en la cual V = velocidad media del flujo, D = profundidad hidráulica, y g =
aceleración gravitacional. A diferencia de la constante k en la ley de Froude (Ec. 1), el número de Froude F en la Ec. 2 es adimensional. En la hidráulica de canales abiertos, la longitud del barco L (una cantidad medida en dirección horizontal) ha sido reemplazada por la profundidad hidráulica D (una medida vertical) con el fin de tomar en cuenta adecuadamente la fuerza de gravitación.

Estos modelos fueron construidos por Froude con el fin de establecer leyes de resistencia y escala aplicables al diseño de los cascos de los barcos.
3. VALENTIN V. VEDERNIKOV: UNA BREVE BIOGRAFÍA
Valentin Valentinovich Vedernikov, doctor en ciencias técnicas (terminología ruso/soviética; un nivel por encima del doctorado en el mundo occidental), se graduó en el Instituto Politécnico del Don (ciudad de Novocherkask, región del óblast de Rostov) en 1928. Trabajó en el Instituto Estatal de Recuperación de Tierras Agrícolas, así como en varias organizaciones de gestión del agua de la región del Cáucaso Norte y el Turkestán, ubicada actualmente en Asia Central. En 1934, Vedernikov publicó un libro titulado Filtración desde canales, en el que utilizó un método de imágenes conformes para el movimiento estable sin presión de agua subterránea en un plano vertical. En este libro utilizó, por primera vez, el método de Vedernikov-Pavlovskiy. Este último se basa en imágenes conformes de regiones de flujo en el plano del potencial complejo de velocidad de filtración y la función compleja de Zhukovkiy. En 1935, Vedernikov obtuvo el doctorado sin defender su tesis; en 1938, defendió su tesis y recibió el título de Doctor en Ciencias Técnicas. Los hallazgos de Vedernikov fueron resumidos en el libro titulado Teoría de la filtración y su uso en los campos de irrigación y drenaje, publicado en 1939. En 1940-1941, Vedernikov fue presidente del Departamento de Hidráulica e Hidromaquinaria en el Instituto Turf de Moscú. En 1941-1942 trabajó en el Instituto de Mecánica de la Academia de Ciencias de la URSS. A partir de 1943, trabajó en la Sección de Investigación Científica en Hidráulica de la Academia Soviética de Ciencias. En 1947 fue nombrado Director del Departamento de Hidráulica del Instituto de Educación de Energía a Distancia de la Unión Soviética.
Entre 1945 y 1947, Vedernikov explicó primero en forma teórica, y luego experimentalmente,
el fenómeno del flujo inestable de agua en canales, con la consecuente formación de ondas de rollo,
definiendo el criterio de inestabilidad del flujo (Fig. 2). Para llevar a cabo esta tarea,
utilizó las ecuaciones de Saint-Venant del flujo inestable en canales abiertos.
En la literatura de ingeniería hidráulica, su concepto se conoce como el número de Vedernikov
(Powell, 1948;
Chow, 1959).
4. VELOCIDADES EN FLUJO EN CANAL ABIERTO
Flujo permanente: Velocidad media
Existen tres velocidades claramente definidas en el flujo en canal abierto (Ponce, 1991).
u = C (RS) 1/2
en la cual u = velocidad media del flujo uniforme o en equilibrio, con unidades de
L/T (m/s);
La fórmula de Manning es
u = (1/n) (R) 2/3 S1/2
en la cual u = velocidad media del flujo uniforme o en equilibrio, en m/s; n = coeficiente de Manning;
y R (en m) y S (en m/m) han sido definidos previamente. La fórmula de Manning en
unidades habituales de los EE. UU. es:
u = (1.486/n) (R) 2/3 S1/2
en la cual R (en pies) y S (en pies/pies).
Si bien la ecuación de Manning suele preferirse en la práctica,
la ecuación de Chezy puede expresarse en forma adimensional, lo que
constituye una ventaja, en particular para estudios teóricos
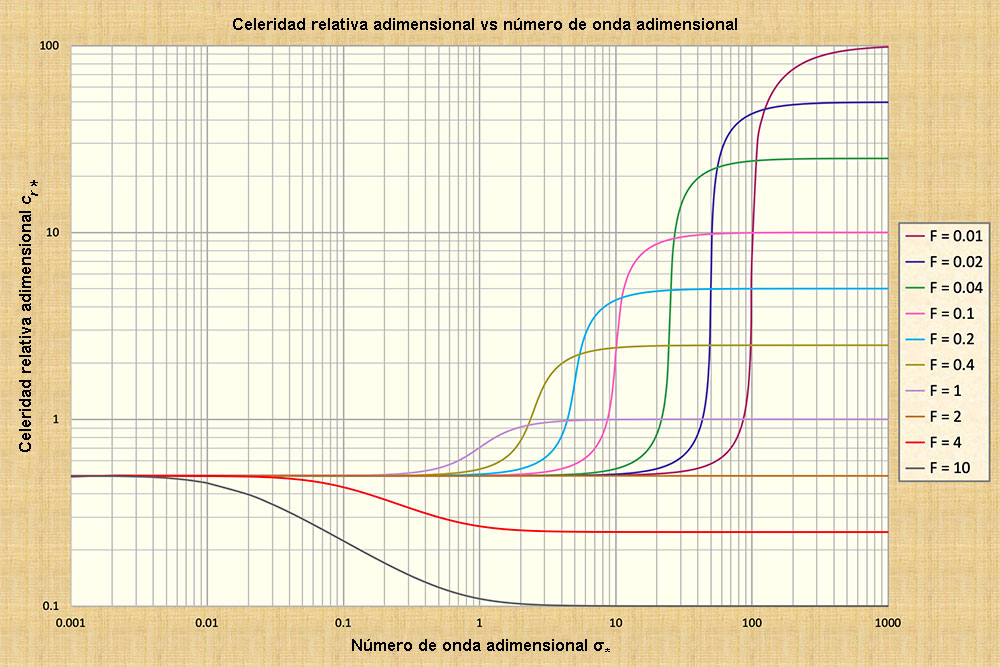
Las Ecuaciones 3 a 5 calculan la velocidad media u, es decir, la velocidad del flujo uniforme o en equilibrio. El resto de esta sección describirá las otras dos velocidades en el flujo en canal abierto, es decir, las velocidades o, más propiamente, las celeridades que caracterizan el flujo inestable. Flujo inestable: Dos celeridades de onda Existen dos celeridades de onda que completan la tríada de velocidad/celeridades en el flujo en canal abierto: (1) la celeridad de la onda cinemática; y (2) la celeridad de la onda dinámica. Una onda cinemática es una perturbación superficial "grande", es decir, una onda que presenta un número de onda adimensional pequeño, en el sentido de Ponce y Simons (1977). Por el contrario, una onda dinámica es una perturbación superficial "pequeña", es decir, una onda que presenta un número de onda adimensional grande.
La diferencia entre ondas cinemáticas y dinámicas está representada admirablemente
en el gráfico de celeridades de onda adimensionales relativas vs. números de
onda adimensionales (Fig. 3).
La celeridad de la onda cinemática es: ck = βu, en la cual
β es el exponente de la
relación
La celeridad de la onda dinámica tiene dos componentes: cd = u ± (gD)1/2,
en la cual g = aceleración gravitacional, y D = A/T = profundidad hidráulica.
Por lo tanto, la celeridad relativa de la onda dinámica
(es decir, la celeridad relativa a la velocidad media)
es:
En resumen, las tres velocidades (una velocidad y dos celeridades) preeminentes
en el flujo en canal abierto, incluyendo tanto el flujo permanente como el
impermanente, son: (1) u = velocidad media del flujo,
En este artículo demostramos que estas tres velocidades/celeridades (u, v y w) pueden producir sólo
dos números adimensionales independientes: (1) el número de Froude, y (2) el número de
Vedernikov.
5. EL NÚMERO DE FROUDE
El número de Froude se define como la relación entre la velocidad media del flujo u
y la celeridad relativa de la onda dinámica w (Ponce, 1991):
F = u /w
En otras palabras, el número de Froude compara la velocidad media del
flujo con la celeridad relativa de pequeñas perturbaciones
en la superficie. Hay tres situaciones posibles:
Para w > u, entonces F < 1 y el flujo se encuentra en estado
subcrítico. Como w > u, el resultado de (u - w) es menor que 0
y la perturbación
puede propagarse aguas arriba, es decir, el flujo puede controlarse sólo
desde una localización aguas abajo.
Para w = u, entonces F = 1,
y el flujo se encuentra en estado crítico.
Como w = u, el resultado de (u - w) es igual a 0,
y la perturbación permanece estacionaria,
siendo incapaz de trasladarse ya sea aguas arriba como aguas abajo. En la práctica,
un estado de flujo crítico es inusual; su presencia se revela por la
aparición de pequeñas perturbaciones superficiales, a menudo con
una marcada tendencia a persistir (Fig. 4).
Para w < u, entonces F > 1, y el flujo está en estado
supercrítico.
Como w < u, el resultado de
6. EL NÚMERO DE VEDERNIKOV
El número de Vedernikov se define como la relación entre la celeridad relativa
de las ondas cinemáticas v y la celeridad relativa de las ondas dinámicas
w (Ponce, 1991):
V = v /w
En otras palabras, el número de Vedernikov compara la celeridad relativa
de ondas cinemáticas "grandes" (de pequeño número de onda adimensional),
es decir, aquéllas impulsadas por gradientes de masa, con la celeridad
relativa de ondas dinámicas "pequeñas" (de gran número de onda
adimensional), es decir, aquéllas impulsadas por gradientes
de energía
Para w > v, entonces V < 1 y el flujo está en estado estable.
Como w > v,
se deduce que
Para w = v, entonces V = 1 y el flujo está en un estado neutralmente estable.
Como w = v, se deduce que
Para w < v, entonces V > 1 y el flujo está en estado inestable. Como w < v,
se deduce que
Estas afirmaciones se resumen en la Tabla 3.
Fig. 5 Ondas de rollo en un canal de riego, Cabana-Mañazo, Puno, Perú.
7. EL EXPONENTE DE LA CURVA DE GASTO
La tercera relación de un total de tres, además de (1) F = u /w, y
(2) V = v /w
V/F = v /u
Es de notar que la celeridad de la onda cinemática (Sección 4) es:
ck = βu, en la cual β es el
exponente de la curva de gasto
V/F = β - 1
En otras palabras, el exponente β de la curva de gasto
Q = αAβ encapsula
los números de Froude y Vedernikov, de modo que β = (V/F) + 1.
Además, para V = 1, es decir, para flujo neutralmente estable,
el número de Froude neutralmente estable es:
Fns = 1 / (β - 1). Por ejemplo, para β = 1.5,
es decir, para la fricción de Chezy en un canal hidráulicamente ancho: Fns = 2.
Este hallazgo se confirma en la Fig. 3, en la que la línea horizontal, aplicable
para F = 2, permanece constante para todos los tamaños de onda, cinemática y dinámica,
y no atenúa ni amplifica (F= 2 corresponde al estado neutralmente estable, aplicable
para la fricción de Chezy en canales hidráulicamente anchos).
La Tabla 4 muestra la variación del número de Froude neutralmente estable Fns
con el exponente β
Las conclusiones anteriores merecen la elevación del exponente
β de la curva de gasto a una posición privilegiada en el campo
de la hidráulica de canales abiertos. El exponente β contiene
exclusivamente la relación entre los números de Froude y Vedernikov, al mismo tiempo que
describe las propiedades de fricción y de forma de la
sección transversal (Tabla 4). Se reconoce que el número de Vedernikov, el cual
varía con el tipo de fricción y forma de la sección transversal, constituye el
hallazgo original de Vedernikov
(1945,
1946),
aunque él no lo haya presentado de esta manera [Chow (1959):
8. COMENTARIOS FINALES
Hemos demostrado que sólo hay tres velocidades (más correctamente,
una velocidad y dos celeridades) que caracterizan
el flujo en canales abiertos en una amplia variedad de aplicaciones en
flujo estable e inestable, incluyendo el diseño de canales,
control de flujo, enrutamiento de inundaciones e inestabilidad del flujo. Estas son: (1) la velocidad media
del flujo u, (2) la celeridad relativa de las ondas cinemáticas
v, y (3) la celeridad relativa de las ondas dinámicas w.
Estas tres velocidades dan lugar a sólo dos números adimensionales independientes:
(1) el número de Froude F = u/w, y (2) el número de Vedernikov V = v/w.
La tercera relación, v/u,
propiamente V/F, es igual a (β - 1), en la cual β
es el exponente de la curva de gasto caudal-area de flujo
Q = αAβ.
REFERENCIAS
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York, NY.
Extracto: Página 210.
Lagrange, J. L. de. 1788. Mécanique analytique, Paris, part 2, section II, article 2, 192.
Ponce, V. M. y D. B. Simons. 1977.
Propagación de ondas poco profundas en canales abiertos.
Artículo en linea.
Ponce, V. M. 1991. Nueva perspectiva del número de Vedernikov.
Artículo en linea.
Ponce, V. M. 2014.
Fundamentos de la hidráulica de canales. Texto en línea..
Ponce, V. M. 2023a.
Los estados de flujo. Artículo en línea.
Ponce, V. M. 2023b.
El número de Vedernikov. Artículo en línea.
Ponce, V. M. y B. Choque Guzman. 2024.
Control de ondas de rollo en ríos
canalizados de alta pendiente.
Artículo en línea.
Powell, R. W. 1948.
Vedernikov's criterion for ultra-rapid flow.
Transactions, American Geophysical Union, 29(6), 882-886.
Seddon, J. A. 1900. River Hydraulics.
Transactions, American Society of Civil Engineers, XLIII(179-243), June;
Vedernikov, V. V. 1945.
Vedernikov, V. V. 1946.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 250122 |