Río Alto Paraguay en Porto Murtinho, Mato Grosso do Sul, Brasil, el cual muestra un hidrograma de inundación de un año de duración, lo cual constituye la onda de inundación cinemática por excelencia.


EL NÚMERO DE PONCE-SIMONS


Víctor M. Ponce

Profesor Emérito de Ingeniería Civil y Ambiental

Universidad Estatal de San Diego, California, EE.UU.


 17 de mayo de 2024

RESUMEN.  Las tres difusividades de la mecánica de fluidos y el flujo en canales abiertos (molecular, hidráulica y espectral) se definen y explican en forma detallada. Este artículo trata el número de Ponce-Simons, la relación de difusividades hidráulica y espectral, afectada con el factor 2π. Este número caracteriza la escala espacial y propiedades asociadas de las perturbaciones superficiales en el flujo no permanente en canales abiertos.

1.  INTRODUCCIÓN

En la ingeniería hidráulica, la viscosidad, o su sinónimo, la difusividad, es una propiedad fundamental de un fluido. La difusividad es el primer momento de la velocidad. Por lo tanto, las unidades de difusividad son (L/T)L, o su expresión equivalente L2/T. La igualdad ν = 1 m2/sec describe la certeza matemática de que una perturbación dada se difundirá con una difusividad de ν = 1 (m/s)m = 1 m2/s. En mecánica de fluidos, la difusividad está relacionada con el proceso de difusión; en ingeniería hidrológica, con la atenuación o disipación de las ondas de inundación. En la modelación matemática hidráulica, la difusividad se describe mediante el término de segundo orden de la ecuación diferencial de gobierno (Tabla 1).

Tabla 1. Comparación de velocidades y difusividades en flujo en canales abiertos.
Propiedad Símbolo Unidades Proceso Orden
VelocidaduL/T Convección, advección Primero
Difusividad ν L2/T Difusión, disipaciónSegundo

Las propiedades enumeradas en la Tabla 1 describen el flujo hasta el segundo orden. En este artículo, enfocamos el número de Ponce-Simons, una relación de difusividades la cual caracteriza la escala espacial de los fenómenos ondulatorios. Una mayor comprensión de este número mejora significativamente el entendimiento del flujo no permanente en canales abiertos.

2.  DIFUSIVIDADES EN EL FLUJO EN CANALES ABIERTOS

Se reconocen tres difusividades en el flujo en canales abiertos:

  1. Difusividad molecular,

  2. Difusividad hidráulica, y

  3. Difusividad espectral.

En la mecánica de fluidos, la difusividad molecular νm se conoce comúnmente como viscosidad cinemática ν, una medida de la resistencia interna del flujo. En el flujo en canales abiertos, la difusividad hidráulica νh se expresa en términos del caudal por unidad de ancho y la pendiente de fondo. En el flujo no permanente, la difusividad espectral νs se define en términos de la longitud de onda de la perturbación sinusoidal. El Cuadro A explica estos conceptos con más detalle.

Cuadro A.  Difusividades en el flujo en canales abiertos.

  1. La ley de viscosidad de Newton es: τ /ρ = ν (∂u/∂s), en la cual τ = esfuerzo cortante, ρ = densidad del fluido, ν = viscosidad cinemática del fluido (difusividad molecular), y (∂u/∂s) = gradiente de velocidad en la dirección s perpendicular a la dirección de τ. Para nuestro propósito:

    τ /ρ = νm (∂u/∂s)

    La difusividad molecular se puede expresar como νm = u (Lm /2), en la cual Lm = (2νm /u)  es una longitud molecular característica (Chow, 1959).

  2. La difusividad hidráulica se define como νh = u (Lo /2), en la cual Lo = (do /So) es una longitud hidráulica característica, definida como la distancia medida a lo largo del canal en la cual el flujo pierde una carga igual a la profundidad de equilibrio (Hayami, 1951; Ponce y Simons, 1977).

  3. La difusividad espectral νs se define como νs = u (L /2), en la cual L = longitud de onda característica de la perturbación superficial sinusoidal (Ponce, 1979).

    Nótese que las tres difusividades (molecular, hidráulica y espectral) se definen en términos de sus respectivas longitudes características: (1) longitud molecular Lm, (2) longitud hidráulica Lo, y (3) longitud de onda L. Obsérvese que las tres difusividades comparten una estructura similar: La velocidad convectiva multiplicada por un medio de la longitud característica respectiva.

3.  EL NÚMERO DE PONCE-SIMONS

Las tres difusividades identificadas en el Cuadro A dan lugar a sólo dos números adimensionales independientes (Ponce, 2023b):

  1. La relación entre la difusividad hidráulica y la molecular, un tipo de número de Reynolds; y

  2. La relación entre la difusividad hidráulica y la espectral, un tipo de número de Ponce-Simons.

Ponce y Simons (1977), en su trabajo fundamental sobre la propagación de ondas poco profundas, definieron un número de onda adimensional de la siguiente manera: σ* = (2π /L)Lo. Obsérvese que el número de Ponce-Simons es de hecho un sustituto de una relación de difusividades, ya que: σ* = (2π /L)Lo = 2π (νh /νs).

El número de onda adimensional de Ponce-Simons σ* clasifica el ámbito de las perturbaciones del flujo inestable en cuatro segmentos espectrales (Fig. 1):

  1. Cinemático (extremo izquierdo),

  2. Difusión (centro-izquierda),

  3. Cinemático-dinámico mixto (centro-derecha), y

  4. Dinámico (extremo derecho).

Ponce (2023a) ha examinado los dominios precisos de estos segmentos, o rangos:

  • Flujo cinemático: σ* < 0.001.

  • Flujo de difusión: 0.001 ≤ σ* < 0.17.

  • Flujo cinemático-dinámico mixto: 0.17 ≤ σ* < 1 to 100, dependiendo del número de Froude (véase la Fig. 1).

  • Flujo dinámico: σ* ≥ 10 to 1000, dependiendo del número de Froude (Fig. 1).

Ponce y Simons (1977)

Fig. 1   Celeridad de onda relativa adimensional cr* vs número de onda adimensional σ*.

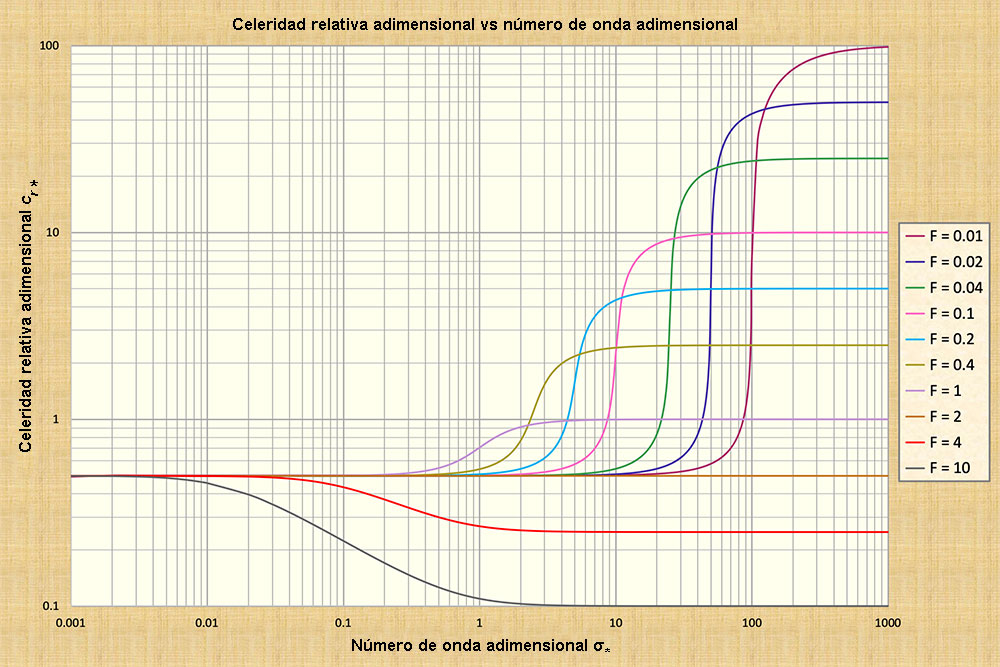
Los hallazgos de Ponce y Simons (1977), representados en la Fig. 1, aclaran el comportamiento de todos los tipos de ondas en el flujo no permanente en canales abiertos. Éstas incluyen tanto las ondas "largas", de naturaleza cinemática, hacia el extremo izquierdo de la Fig. 1, como ondas "cortas", de naturaleza dinámica, hacia el extremo derecho; estas ondas presentan una celeridad constante. También se incluyen las ondas de difusión, hacia el centro-izquierda, las cuales muestran propiedades que son bastante prácticas, y las ondas cinemático-dinámicas mixtas hacia el centro-derecha. Estas últimas ondas son, en su mayor parte, poco prácticas debido a sus tendencias disipativas muy fuertes (Ponce, 2023a).

4.  RESUMEN

Las tres difusividades de la mecánica de fluidos y el flujo en canales abiertos (molecular, hidráulica y espectral). se definen apropiadamente. Este artículo enfoca el número de Ponce-Simons, la relación de difusividades hidráulica y espectral, afectada por el factor 2π. Este número adimensional caracteriza la escala espacial y las propiedades de perturbaciones superficiales en el flujo no permanente en canales abiertos.

BIBLIOGRAFÍA

Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York, NY.

Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December, Extract.

Ponce, V. M. y D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering ASCE, 103(12), 1461-1476. En Español: Propagación de ondas poco profundas en canales abiertos.

Ponce, V. M. 1979. On the classification of open channel flow regimes. Proceedings, Fourth National Hydrotechnical Conference, Vancouver, British Columbia, Canada. En Español: Clasificación de los regímenes de flujo en canales.

Ponce, V. M. 2023a. When is the diffusion wave applicable? Online article.

Ponce, V. M. 2023b. Ths states of flow. Online article. En Español: Los estados de flujo.

240517